Prel语言入门学习:一篇全面的指南
引言
在编程语言的海洋中,Prel是一个较少人知的新星。作为一种专为数据处理和分析设计的语言,Prel结合了现代编程语言的简洁性与功能性,提供了一种独特的解决方案,尤其适用于数据科学家和分析师。本文将详细介绍Prel语言的基础,包括其设计哲学、安装过程、基本语法、常用功能以及如何在实际项目中应用Prel进行数据分析。
第一部分:Prel语言概述
- Prel的设计哲学
Prel语言的设计旨在简化数据处理流程,使得从数据导入到处理再到导出的过程更加高效和直观。Prel支持多种数据源,如CSV、JSON、XML等,也可以直接与SQL数据库交互。它的核心设计哲学包括:
简洁性:语法简单,易于学习和使用。
灵活性:可扩展的功能,支持各种数据操作和算法实现。
效率:优化的执行引擎,快速处理大规模数据集。
2. Prel的主要特点
内置数据操作功能:如过滤、排序、分组和聚合。
强大的数学和统计函数库:支持高级数据分析和机器学习。
直观的数据可视化工具:内置功能支持生成图表和报告。
第二部分:安装Prel
- 系统要求
Prel可以在Windows、macOS和Linux系统上运行。安装前需要确保系统中已安装Python环境(Python 3.6及以上版本)。
- 安装步骤
安装Prel最简单的方式是通过Python的包管理器pip。打开命令行工具,执行以下命令:
pip install prel-lang此命令将从Python的包索引中下载并安装最新版本的Prel语言及其依赖。
第三部分:Prel基础语法和操作
- 基本数据类型和变量
Prel的基本数据类型包括整数、浮点数、字符串、布尔值等。变量的声明非常简单,无需指定类型,例如:
x = 10
y = 3.14
name = "Data Analysis"- 数据结构
Prel支持列表(List)、字典(Dictionary)、集合(Set)等复杂数据结构。例如:
# 列表
data_list = [1, 2, 3, 4, 5]# 字典
data_dict = {"name": "Alice", "age": 30}# 集合
data_set = set([1, 2, 3, 1, 2])- 控制流
Prel的控制流语句包括if条件判断、for和while循环等,语法与其他主流编程语言类似。
# if 条件判断
if x > 0:print("x 是正数")# for 循环
for i in data_list:print(i)# while 循环
while x > 0:print(x)x -= 1- 函数定义
Prel允许用户定义函数,以复用代码和处理复杂逻辑。
def square(x):return x * xresult = square(5)
print(result)第四部分:Prel在数据分析中的应用
- 数据加载和预处理
Prel可以加载各种格式的数据文件,提供了强大的数据清洗、转换和预处理功能。
# 加载CSV文件
data = load_csv("data.csv")# 数据清洗
clean_data = data.dropna().filter("age > 18")- 数据分析
使用Prel进行数据分析,可以利用其内置的统计函数和数据操作功能。
# 数据描述
description = clean_data.describe()# 分组聚合
summary = clean_data.groupby("department").agg({"salary": "mean"})- 数据可视化
Prel支持直接生成图表,如柱状图、线图等,方便进行数据可视化分析。
# 生成柱状图
bar_chart = clean_data.plot.bar("department", "salary")
bar_chart.show()结论
Prel语言为数据科学家和分析师提供了一个强大、灵活而高效的工具,使他们能够轻松处理和分析大规模数据集。通过本文的介绍,读者应该能够掌握Prel的基本用法,并能够开始利用Prel进行实际的数据分析项目。随着对Prel更深入的学习和实践,用户将能更充分地发挥其在数据科学中的巨大潜力。
相关文章:

Prel语言入门学习:一篇全面的指南
引言 在编程语言的海洋中,Prel是一个较少人知的新星。作为一种专为数据处理和分析设计的语言,Prel结合了现代编程语言的简洁性与功能性,提供了一种独特的解决方案,尤其适用于数据科学家和分析师。本文将详细介绍Prel语言的基础&am…...

在云服务器上自动化部署项目,jenkins和gitee
▮全文概述 在编写项目时,很头大的事情就是需要自己手动的上传jar包到服务器上启动。如果出现一点bug,就要重头上传和启动。这是一件很烦的事情,所以,可以使用jenkins和gitee实现项目的自动部署 ▮全流程 在本地提交代码到gitee …...

python 参数输入
在 Python 中,参数输入通常有多种方式,这取决于你要从何处获取参数。以下是几种常见的方法: 1. 命令行参数 使用 sys.argv 获取命令行参数,或者使用 argparse 模块进行更复杂的参数解析。 示例 1: 使用 sys.argv import sys# …...

Spring面试篇章——Spring基本概述
Spring 的基本概述 Spring学习的核心内容—一图胜千言 IOC:控制反转,可以管理 Java 对象AOP:切面编程JDBCTemplate:是Spring提供一套访问数据库的技术,应用性强,相对好理解声明式事务:基于IOC …...

股票预测模型中注意力多层Attention RNN LSTM 的应用
全文链接:https://tecdat.cn/?p37152 原文出处:拓端数据部落公众号 Attention 机制是一种在神经网络处理序列数据时极为关键的技术,它赋予了模型“聚焦”能力,能够自动评估输入序列中各部分的重要性。通过为序列中的每个元素分…...

C语言 | Leetcode C语言题解之第313题超级丑数
题目: 题解: int nthSuperUglyNumber(int n, int* primes, int primesSize) {long dp[n 1];int pointers[primesSize];for (int i 0; i < primesSize; i) {pointers[i] 0;}long nums[primesSize];for (int i 0; i < primesSize; i) {nums[i] …...
PHP健身微信小程序系统源码
🏋️♀️健身新潮流!解锁“健身微信小程序”的全方位塑形秘籍 📱开篇:掌中健身房,随时随地动起来 你还在为找不到合适的健身场地或教练而烦恼吗?是时候告别这些束缚,拥抱“健身微信小程序”…...

树组件 el-tree 数据回显
树组件 el-tree 数据回显 树型结构的数据回显问题: 这里我只放了核心代码,主要是如何获取选中的树节点的id集合和如何根据树节点的id集合回显数据 大家根据需要自行更改! <el-tree ref"authorityRef" node-key"id" …...

54、PHP 实现希尔排序
题目: PHP 实现希尔排序 描述: 思路分析:希尔排序是基于插入排序的,区别在于插入排序是相邻的一个个比较(类似于希尔中h1的情形),而希尔排序是距离h的比较和替换。 希尔排序中一个常数因子n&a…...

linux 虚拟机解压arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2并arm-linux-gcc
解压到当前目录:tar -jxvf arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2解压到指定目录:tar -jxvf arm-linux-gcc-4.6.4-arm-x86_64.tar.bz2 -C /xx/xxx/xxx-C大写,后面接要解压的路径解压后得到一个 opt文件夹 在/usr/local/bin 下创建新的…...

泛化的最近点迭代法(Generalized-ICP)
Generalized-ICP算法是由斯坦福大学的Aleksandr V. Segal、Dirk Haehnel和Sebastian Thrun提出的,于2009年在Robotics science and system会议上发表。 GICP是一种ICP算法的变体,其原理与ICP算法相同,之所以称为泛化的ICP算法是因为大多数ICP…...

Java | Leetcode Java题解之第313题超级丑数
题目: 题解: class Solution {public int nthSuperUglyNumber(int n, int[] primes) {int[] dp new int[n 1];int m primes.length;int[] pointers new int[m];int[] nums new int[m];Arrays.fill(nums, 1);for (int i 1; i < n; i) {int minN…...

单细胞数据整合-去除批次效应harmony和CCA (学习)
目录 单细胞批次效应学习 定义 理解 常用的去批次方法-基于Seurat 1) Seurat-integration(CCA) 2) Seurat-harmony 去批次代码 ①Seurat-integration(CCA) ②Seurat-harmony 单细胞批次效应学习 …...

MuRF代码阅读
对图像Size的处理, 以适应Transformer 在MVSPlat 当中使用 Center_Crop 裁剪图像,适用于 Transformer 的32 倍数, 其中 焦距 f 不变化,只改变 cx,cy.MuRF 直接对图像进行 插值,合成理想的 size. 根据 ori_size 和 inference_size…...

pycharm无法导入pyside2模块;“ModuleNotFoundError: No module named ‘PySide2“
参考博客: 1)pycharm中配置pyqt designer和pyside2【功能是在pycharm中可以打开designer,并且可以把.ui文件转换为.py文件】 https://blog.csdn.net/kuntliu/article/details/117219237 2).ui转化为.py后,点击运行,报错…...

c语言指针中“数组名的理解”以及“一维数组传参”的本质
数组名的理解 数组名就是数组首元素的地址。 例如:输入一个数组的所有元素,再打印出来。 另一种写法 以上可以看出:*arri) arr[i] 也即是:*(iarr)i[arr] 本质上无区别 1:数组就是数组,是一块…...

计算机毕业设计Python+Flask微博舆情分析 微博情感分析 微博爬虫 微博大数据 舆情监控系统 大数据毕业设计 NLP文本分类 机器学习 深度学习 AI
基于Python/flask的微博舆情数据分析可视化系统 python爬虫数据分析可视化项目 编程语言:python 涉及技术:flask mysql echarts SnowNlP情感分析 文本分析 系统设计的功能: ①用户注册登录 ②微博数据描述性统计、热词统计、舆情统计 ③微博数…...
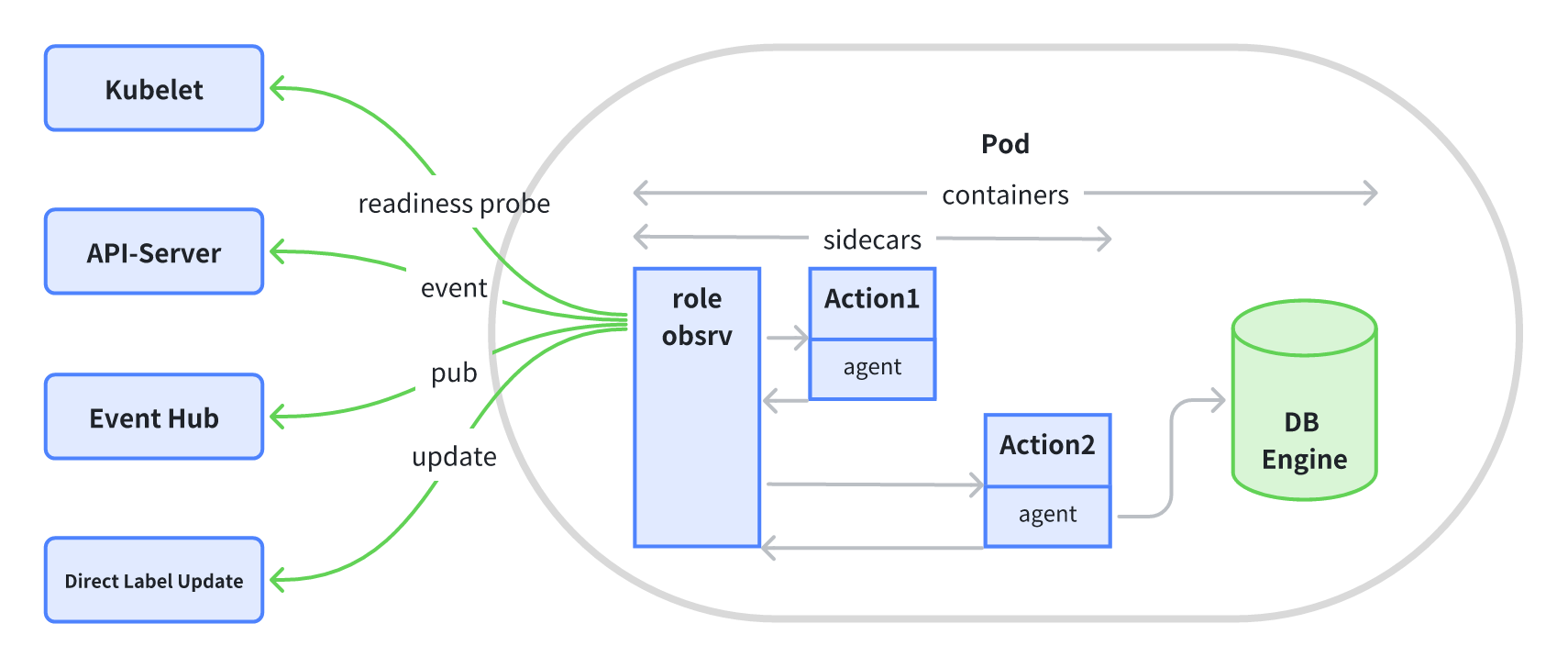
KubeBlocks v0.9 解读|最高可管理 10K 实例的 InstanceSet 是什么?
实例(Instance)是 KubeBlocks 中的基本单元,它由一个 Pod 和若干其它辅助对象组成。为了容易理解,你可以先把它简化为一个 Pod,下文中将统一使用实例这个名字。 InstanceSet 是一个通用 Workload API,负责…...

ZW3D二次开发_菜单_禁用/启用表单按钮
1.如图示,ZW3D可以禁用表单按钮(按钮显示灰色) 2.禁用系统默认表单按钮,可以在菜单空白处右击,点击自定义,找到相关按钮的名称,如下图。 然后使用代码: char name[] "!FtAllBo…...

windows子系统wsl完成本地化设置locale,LC_ALL
在 Windows 的子系统 Linux(WSL)环境中,解决本地化设置问题可以采取以下步骤: 1. **检查本地化设置**: 打开你的 WSL 终端(比如 Ubuntu、Debian 等),运行以下命令来查看当前的本…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
