java之hashCode() 方法和 equals(Object obj) 方法之间的关系
1、 hashCode() 方法和 equals(Object obj)
在Java中,hashCode() 方法和 equals(Object obj) 方法之间的关系是紧密相连的,特别是在使用基于哈希的集合(如 HashSet、HashMap、HashTable 等)时。这两个方法共同决定了对象在哈希表中的存储和检索行为。
hashCode() 方法
hashCode()方法用于获取对象的哈希码。- 哈希码是一个整数,由对象的内部地址或根据对象的字段通过某种算法计算得到。
- 哈希码的主要目的是在哈希表中减少碰撞(即不同的对象具有相同的哈希码)的概率,从而提高查找效率。
equals(Object obj) 方法
equals(Object obj)方法用于比较两个对象是否相等。- 在没有重写
equals方法的情况下,equals方法比较的是对象的引用(即内存地址)。 - 重写
equals方法时,通常也会重写hashCode方法,以保持它们之间的一致性关系。
hashCode() 和 equals(Object obj) 之间的关系
- 一致性(Consistency):对于任何非null的引用值x和y,当且仅当
x.equals(y)为true时,x.hashCode()必须等于y.hashCode()。 - 不同对象可以有相同的哈希码:两个不相等的对象(即
equals(Object obj)返回false)可以有相同的哈希码。 - 如果两个对象相等:根据
equals(Object obj)方法的定义,如果两个对象相等(即equals(Object obj)返回true),那么对这两个对象中的每一个调用hashCode()方法都必须产生相同的整数结果。
为什么需要保持一致性
在基于哈希的集合中,当你尝试添加、查找或删除一个对象时,集合首先会计算该对象的哈希码,以决定它在哈希表中的哪个桶(bucket)中。然后,它会在该桶中遍历所有对象,使用 equals() 方法来查找确切的对象。
如果 hashCode() 方法没有与 equals() 方法保持一致,那么即使两个对象通过 equals() 方法被认为是相等的,它们也可能被放置在哈希表的不同桶中,导致无法正确找到对象,或者导致哈希表无法正确管理对象的存储和检索。
因此,当你重写 equals() 方法时,通常也需要重写 hashCode() 方法,以确保这两个方法之间的一致性。
2、不同对象可以有相同的哈希码的原因
在哈希表中,不同对象可以有相同的哈希码(也称为哈希冲突或哈希碰撞)的原因主要归结为哈希函数的有限性和对象的无限性之间的矛盾。
-
哈希函数的有限性:哈希函数的设计目标是将任意长度的输入(比如对象的状态或关键属性)映射到固定长度的输出(即哈希码,通常是整数)。由于输出空间是固定的,因此哈希函数只能产生有限数量的不同哈希码。
-
对象的无限性:在理论上,可以创建的对象数量是无限的,因为对象的属性可以有无限多种组合方式。即使只考虑有限的几个属性,这些属性的不同组合也会导致理论上无限多种不同的对象。
-
概率性:由于哈希函数的输出空间有限,而输入空间(即可能的对象集合)无限,因此必然存在多个不同的对象映射到同一个哈希码的情况。这是概率上的必然结果,尤其是在处理大量数据时。
-
性能与空间的权衡:哈希表的设计需要在性能(查找、插入和删除操作的平均时间复杂度)和空间(哈希表所需的内存)之间做出权衡。使用更复杂、输出范围更大的哈希函数可以减少哈希冲突,但会增加计算哈希码所需的时间和空间成本。相反,使用更简单、输出范围较小的哈希函数可以提高性能,但会增加哈希冲突的概率。
-
解决哈希冲突:为了处理哈希冲突,哈希表通常使用各种策略,如开放寻址法(open addressing)和链地址法(chaining,也称为分离链接法)。在链地址法中,每个桶(bucket)实际上是一个链表,所有具有相同哈希码的对象都被添加到同一个链表中。这样,即使不同对象具有相同的哈希码,它们也可以被正确地存储和检索。
因此,不同对象可以有相同的哈希码是哈希表设计中的一个固有特性,需要通过合理的哈希函数和冲突解决策略来管理。
3、介绍开放寻址法(open addressing)和链地址法(chaining,也称为分离链接法)
开放寻址法(Open Addressing)和链地址法(Chaining,也称为分离链接法)是两种解决哈希表中哈希冲突的主要方法。下面分别介绍这两种方法:
1. 开放寻址法(Open Addressing)
定义与原理:
- 开放寻址法是一种哈希表的冲突解决方法,它要求所有的元素都存储在哈希表的数组中。当发生冲突时,即两个不同的元素通过哈希函数计算得到的哈希值相同时,开放寻址法会寻找数组中的下一个空闲位置,直到找到一个空槽或遍历整个表为止。
实现方式:
- 线性探测(Linear Probing):当发生冲突时,依次检查下一个位置,直到找到一个空槽或者遍历整个表。公式为
hash(key, i) = (hash(key) + i) % tableSize。 - 二次探测(Quadratic Probing):根据一个二次方程的形式探测下一个位置,公式为
hash(key, i) = (hash(key) + c1 * i + c2 * i^2) % tableSize。 - 双重哈希(Double Hashing):使用两个哈希函数,第一个哈希函数计算出位置,如果发生冲突,则通过第二个哈希函数计算一个步长,再次寻找下一个位置。公式为
hash(key, i) = (hash1(key) + i * hash2(key)) % tableSize。
优势与劣势:
- 优势:不需要额外的数据结构来存储相同哈希值的元素,节省空间。
- 劣势:可能导致聚集(clustering)问题,即相邻的位置可能会被频繁占用,导致查找效率下降。同时,扩容和重新哈希的成本较高。
2. 链地址法(Chaining,分离链接法)
定义与原理:
- 链地址法是一种通过链表解决哈希冲突的方法。在哈希表的每个槽位上,不直接存储数据元素,而是存储一个指向链表的指针。所有映射到该槽位的数据元素都存储在链表中。
实现方式:
- 当哈希函数计算出的槽位已有元素时,将新元素添加到该槽位对应链表的末尾。
- 查找、插入和删除操作都首先定位到槽位,然后在链表中进行。
优势与劣势:
- 优势:处理冲突简单,只需在链表末尾添加新元素。同时,链表的长度可以动态变化,适应不同数量的元素。
- 劣势:在极端情况下,某些槽位的链表可能非常长,导致查找效率下降。此外,链表需要额外的空间来存储指针。
装填因子:
- 在链地址法中,装填因子α定义为哈希表中关键字记录总数N与哈希表大小M的比值,即α=N/M。它反映了哈希表的填充程度,对哈希表的性能有重要影响。
综上所述,开放寻址法和链地址法各有优缺点,选择哪种方法取决于具体的应用场景和需求。
相关文章:
 方法和 equals(Object obj) 方法之间的关系)
java之hashCode() 方法和 equals(Object obj) 方法之间的关系
1、 hashCode() 方法和 equals(Object obj) 在Java中,hashCode() 方法和 equals(Object obj) 方法之间的关系是紧密相连的,特别是在使用基于哈希的集合(如 HashSet、HashMap、HashTable 等)时。这两个方法共同决定了对象在哈希表…...

首届「中国可观测日」圆满落幕
首届中国可观测日(Observability Day)在上海圆满落幕,为监控观测领域带来了一场技术盛宴。作为技术交流的重要平台,此次活动不仅促进了观测云与亚马逊云科技之间的深化合作,更标志着双方共同推动行业发展的重要里程碑。…...

[Docker][Docker NetWork][下]详细讲解
目录 1.网络管理命令1.docker network creatre2.docker network inspect3.docker network connect4.docker network disconnect5.docker network prune6.docker network rm7.docker network ls 2.docker bridge 详解0.基本概念1.默认 bridge2.自定义 bridge3.DNS解析4.端口暴露…...

安卓系统在未来如何更好地解决隐私保护与数据安全的问题?
安卓系统可以通过以下方式更好地解决隐私保护与数据安全的问题: 强化权限控制:安卓系统可以进一步加强对应用程序权限的管理,确保用户能够清楚地知道应用程序需要哪些权限,并给予用户更多的控制权,例如允许用户选择性地…...

MySQL innodb单表上限一般多少
参考:https://www.zhihu.com/question/351797203/answer/3137174084 1.MySQL innodb单表上限为啥都说是2k万条 2.GaussDB for MySQL 为啥可以突破单表2k万的限制 要讨论这两个问题,得先明确性下实际的DB部署环境 表是索引数据是放在磁盘上的…...
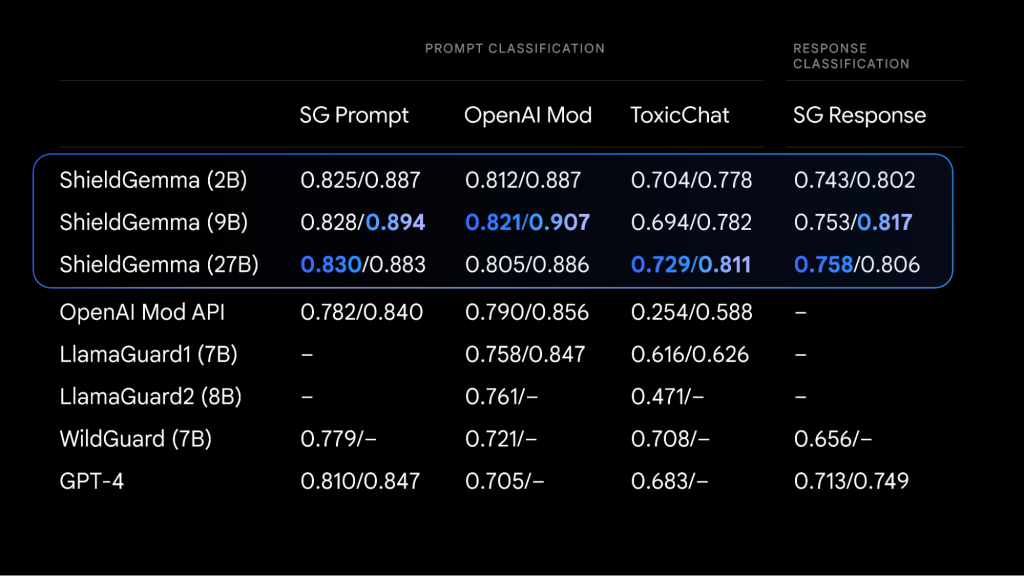
更小、更安全、更透明:Google发布的Gemma推动负责任AI的进步
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

基于Django框架的医疗耗材管理系统的设计实现-计算机毕设定制-附项目源码(可白嫖)48999
摘 要 在目前的形势下,科技力量已成为我国的主要竞争力。而在科学技术领域,计算机的使用逐渐达到成熟,无论是从国家到企业再到家庭,计算机都发挥着其不可替代的作用,可以说计算机的可用领域遍及生活、工作的各个方面。…...
:modbus tcp和modbusRTU的区别是什么?)
物联网协议篇(1):modbus tcp和modbusRTU的区别是什么?
Modbus TCP和Modbus RTU是Modbus协议中的两种主要变体,它们在多个方面存在显著的区别。以下是它们之间的主要区别: 1. 物理层和数据传输方式 Modbus TCP (TCP/IP): 使用以太网作为物理层,通过TCP/IP协议进行通信。数据以数据包的形式在TCP连接上传输,具有较高的通信速度和…...

JVM系列 | 对象的消亡——HotSpot的设计细节
HotSpot 的细节实现 文章目录 HotSpot 的细节实现OopMap 与 根节点枚举根节点类型及说明HotSpot中的实现 OopMap 与 安全点安全点介绍如何保证程序在安全点上? 安全区域记忆集与卡表记忆集卡表 写屏障并发的可达性分析(与用户线程)并发可达性…...
)
vue 运行或打包过程报错 JavaScript heap out of memory(内存溢出)
安装 increase-memory-limit npm install increase-memory-limit 运行increase-memory-limit ./node_modules/.bin/increase-memory-limit 运行后会报以下错误: "node --max-old-space-size10240" 不是内部或外部命令,也不是可运行的程序…...

git分支提交方法
先下载最新代码 改动文件覆盖 cp 文件到~/file/ git add添加文件 git commit提交本地 建立分支 git diff .c git status -uno git add git commit git checkout -b issue-lyd git push origin issue-lyd...
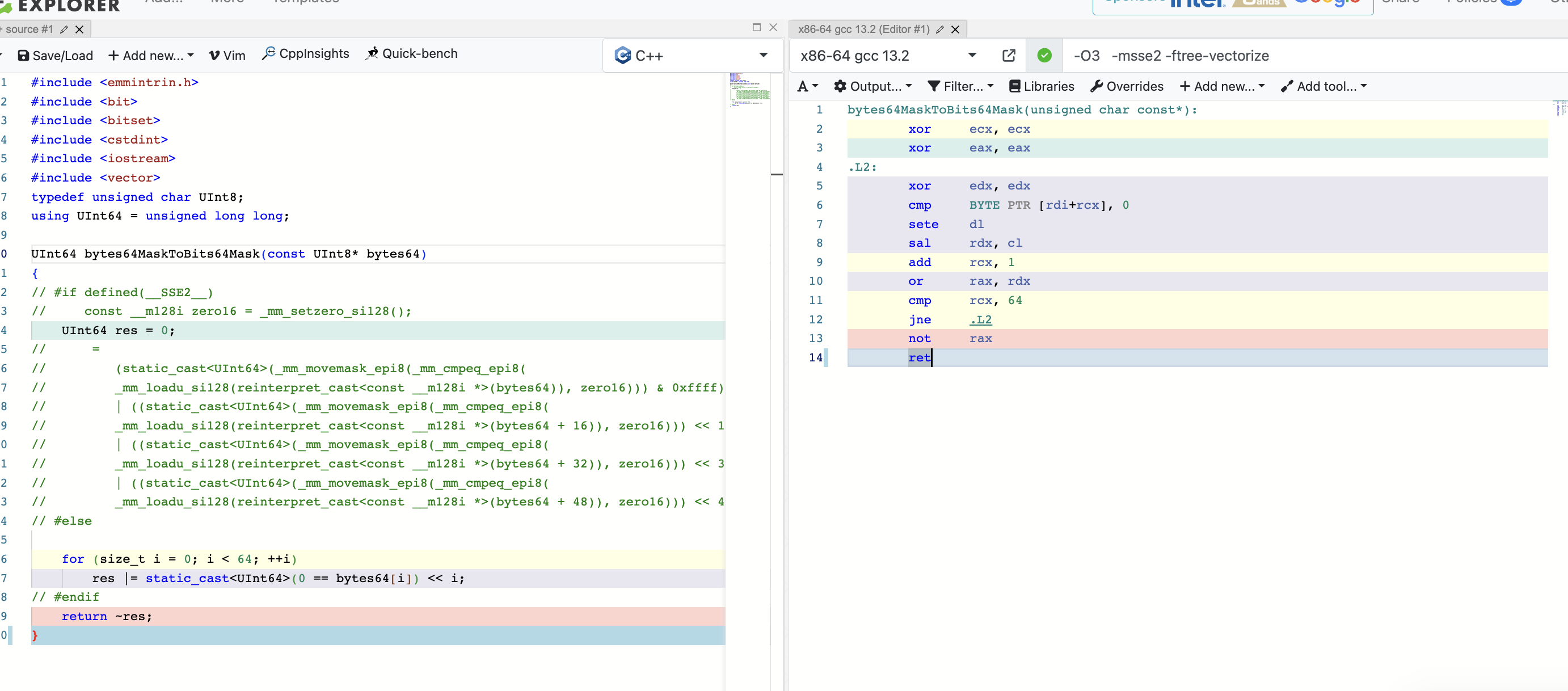
从微架构到向量化--CPU性能优化指北
引入 定位程序性能问题,相信大家都有很多很好的办法,比如用top/uptime观察负载和CPU使用率,用dstat/iostat观察io情况,ptrace/meminfo/vmstat观察内存、上下文切换和软硬中断等等,但是如果具体到CPU问题,我…...

声声入耳,事事如意 爱可声「如意」助听器即将上市!
如意助听器 Charm 爱可声全新系列「如意」助听器即将上市! 此次新品充分考虑了不同听损以及年龄的用户需求, 融合三大强劲性能。 1、多群体覆盖,定制个性化方案 如意助听器针对不同听损程度的听障患者设计了不同款式助听器,贴…...

生物实验室设备文件采集如何才能质量和效率双管齐下?
生物实验室的设备文件采集是实验室运营、科研活动和数据科学实践应用中不可或缺的一环。通过数据采集,实验室可以优化资源配置、提高实验结果的准确性和可靠性、支持科研水平的提升,并确保数据的安全性和可追溯性。因此,实验室应高度重视设备…...

Framework源码整编、单编、烧录过程
目录 一.背景 二.整编方式 二.单编方式 三.烧录 一.背景 源码编译分为整编和单编,整编通常耗时较长,单编则速度很多,如果我们进行一个小的修改想要立马验证的话单编就很合适 二.整编方式 开始执行编译操作,总共三步. 执行source操作source build/envsetup.sh .执行lunc…...

TypeScript类型断言
TypeScript类型断言是TypeScript中一个强大且有用的特性,它允许开发者在编译时明确指定一个值的类型,即使TypeScript无法自动推断出这个类型。类型断言类似于其他编程语言中的类型转换,但它不会改变变量的运行时值,而只是告诉编译…...
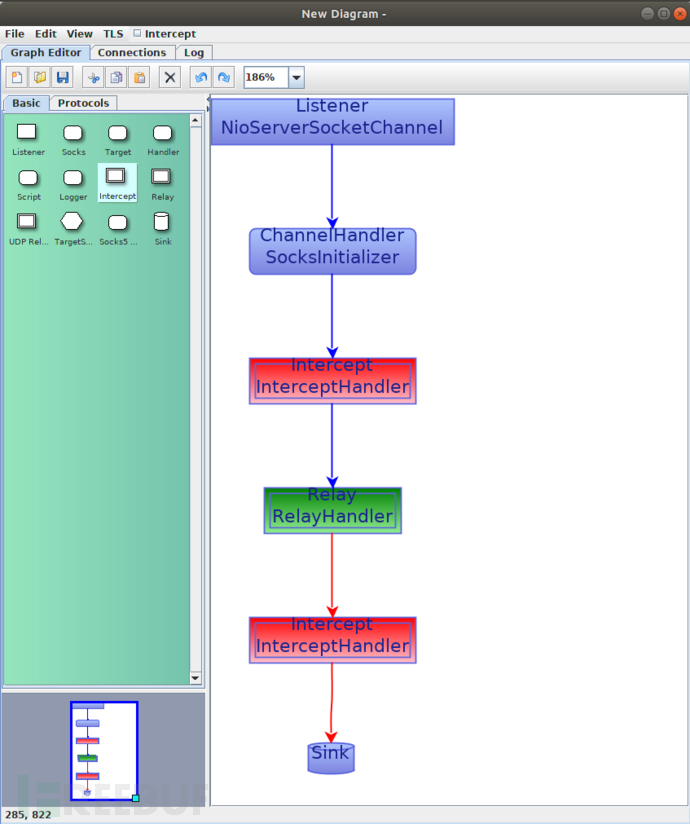
Mallet:一款针对任意协议的安全拦截代理工具
关于Mallet Mallet是一款功能强大的协议安全分析工具,该工具支持针对任意协议创建用于安全审计的拦截代理,该工具本质上与我们所熟悉的拦截Web代理类似,只是通用性更强。 工具运行机制 Mallet建立在Netty框架之上,并且依赖于Net…...

【IEEE出版】第五届大数据、人工智能与软件工程国际研讨会(ICBASE 2024,9月20-22)
第五届大数据、人工智能与软件工程国际研讨会(ICBASE 2024)将于2024年09月20-22日在中国温州隆重举行。 会议主要围绕大数据、人工智能与软件工程等研究领域展开讨论。会议旨在为从事大数据、人工智能与软件工程研究的专家学者、工程技术人员、技术研发人…...

自修室预约小程序的设计
管理员账户功能包括:系统首页,个人中心,学生管理,公告通知管理,自修室管理,座位预约管理,预约取消管理,管理员管理,系统管理 微信端账号功能包括:系统首页&a…...
用于跟踪个人图书馆的BookLogr
什么是 BookLogr ? BookLogr 是一款网络应用,旨在帮助您轻松管理个人图书馆。这项自托管服务可确保您完全控制数据,提供安全且私密的方式来跟踪您拥有、阅读或希望阅读的所有书籍。您也可以选择向公众自豪地展示您的图书馆,与您的…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
