动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
class Solution {public int fib(int n) {if(n < 2) return n;int[] dp = new int[n + 1];dp[0] = 0; dp[1] = 1;for(int i = 2; i < dp.length; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
class Solution {public int climbStairs(int n) {if(n <= 1) return n;//初始化dp数组int[] dp = new int[n];dp[0] = 1;dp[1] = 2;//递推公式for(int i = 2; i < dp.length; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n-1];}
}746. 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[cost.length + 1];dp[0] = 0;dp[1] = 0;for(int i = 2; i < dp.length; i++){dp[i] = Math.min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);}return dp[dp.length - 1];}
}相关文章:

动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 …...

CSS实现图片边框酷炫效果
一、前言 我们在浏览一些网页时,经常会看到一些好看酷炫的元素边框效果(如下图),那么这些效果是怎么实现的呢?我们知道,一般的边框,要么是实线,要么是虚线(点状…...

遇到 MySQL 死锁问题如何解决?
终于来到死锁检查线程的第三步,可以解决死锁了。 作者:操盛春,爱可生技术专家,公众号『一树一溪』作者,专注于研究 MySQL 和 OceanBase 源码。 爱可生开源社区出品,原创内容未经授权不得随意使用࿰…...

Pyinstaller打包OSError: could not get source code【终极解决】
pyinstaller 打包的时候,发现只要是torch.jit.script装饰的函数,会报以下错误: Traceback (most recent call last):File "torch/_sources.py", line 25, in get_source_lines_and_fileFile "inspect.py", line 1123, i…...
【计算机毕业设计】707高校宿舍管理系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

从C++看C#托管内存与非托管内存
进程的内存 一个exe文件,在没有运行时,其磁盘存储空间格式为函数代码段全局变量段。加载为内存后,其进程内存模式增加为函数代码段全局变量段函数调用栈堆区。我们重点讨论堆区。 托管堆与非托管堆 C# int a10这种代码申请的内存空间位于函…...

Linux进程间通信--IPC之无名管道
进程间通信(IPC,InterProcess Communication)是指在不同进程之间传播或交换信息。 IPC的方式通常有管道(包括无名管道和命名管道)、消息队列、信号量、共享存储、Socket、Streams支持不同主机上的两个进程的IPC。...

Oracle19c数据库system密码锁定
一、在oracle 19c数据库中,cdb中system用户被锁定,locked 二、所在的pdb中的system用户状态是正常的,但不可用,连接的时候提示账号已锁定 三、解决 在cdb中将system用户解锁。 alter user system account unlock;...
 方法和 equals(Object obj) 方法之间的关系)
java之hashCode() 方法和 equals(Object obj) 方法之间的关系
1、 hashCode() 方法和 equals(Object obj) 在Java中,hashCode() 方法和 equals(Object obj) 方法之间的关系是紧密相连的,特别是在使用基于哈希的集合(如 HashSet、HashMap、HashTable 等)时。这两个方法共同决定了对象在哈希表…...

首届「中国可观测日」圆满落幕
首届中国可观测日(Observability Day)在上海圆满落幕,为监控观测领域带来了一场技术盛宴。作为技术交流的重要平台,此次活动不仅促进了观测云与亚马逊云科技之间的深化合作,更标志着双方共同推动行业发展的重要里程碑。…...

[Docker][Docker NetWork][下]详细讲解
目录 1.网络管理命令1.docker network creatre2.docker network inspect3.docker network connect4.docker network disconnect5.docker network prune6.docker network rm7.docker network ls 2.docker bridge 详解0.基本概念1.默认 bridge2.自定义 bridge3.DNS解析4.端口暴露…...

安卓系统在未来如何更好地解决隐私保护与数据安全的问题?
安卓系统可以通过以下方式更好地解决隐私保护与数据安全的问题: 强化权限控制:安卓系统可以进一步加强对应用程序权限的管理,确保用户能够清楚地知道应用程序需要哪些权限,并给予用户更多的控制权,例如允许用户选择性地…...

MySQL innodb单表上限一般多少
参考:https://www.zhihu.com/question/351797203/answer/3137174084 1.MySQL innodb单表上限为啥都说是2k万条 2.GaussDB for MySQL 为啥可以突破单表2k万的限制 要讨论这两个问题,得先明确性下实际的DB部署环境 表是索引数据是放在磁盘上的…...
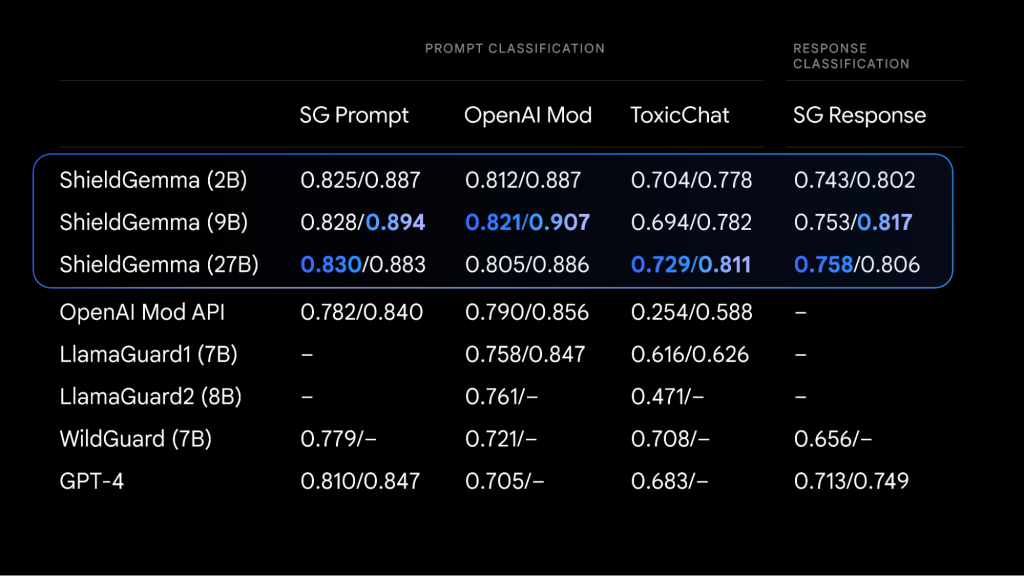
更小、更安全、更透明:Google发布的Gemma推动负责任AI的进步
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

基于Django框架的医疗耗材管理系统的设计实现-计算机毕设定制-附项目源码(可白嫖)48999
摘 要 在目前的形势下,科技力量已成为我国的主要竞争力。而在科学技术领域,计算机的使用逐渐达到成熟,无论是从国家到企业再到家庭,计算机都发挥着其不可替代的作用,可以说计算机的可用领域遍及生活、工作的各个方面。…...
:modbus tcp和modbusRTU的区别是什么?)
物联网协议篇(1):modbus tcp和modbusRTU的区别是什么?
Modbus TCP和Modbus RTU是Modbus协议中的两种主要变体,它们在多个方面存在显著的区别。以下是它们之间的主要区别: 1. 物理层和数据传输方式 Modbus TCP (TCP/IP): 使用以太网作为物理层,通过TCP/IP协议进行通信。数据以数据包的形式在TCP连接上传输,具有较高的通信速度和…...

JVM系列 | 对象的消亡——HotSpot的设计细节
HotSpot 的细节实现 文章目录 HotSpot 的细节实现OopMap 与 根节点枚举根节点类型及说明HotSpot中的实现 OopMap 与 安全点安全点介绍如何保证程序在安全点上? 安全区域记忆集与卡表记忆集卡表 写屏障并发的可达性分析(与用户线程)并发可达性…...
)
vue 运行或打包过程报错 JavaScript heap out of memory(内存溢出)
安装 increase-memory-limit npm install increase-memory-limit 运行increase-memory-limit ./node_modules/.bin/increase-memory-limit 运行后会报以下错误: "node --max-old-space-size10240" 不是内部或外部命令,也不是可运行的程序…...

git分支提交方法
先下载最新代码 改动文件覆盖 cp 文件到~/file/ git add添加文件 git commit提交本地 建立分支 git diff .c git status -uno git add git commit git checkout -b issue-lyd git push origin issue-lyd...
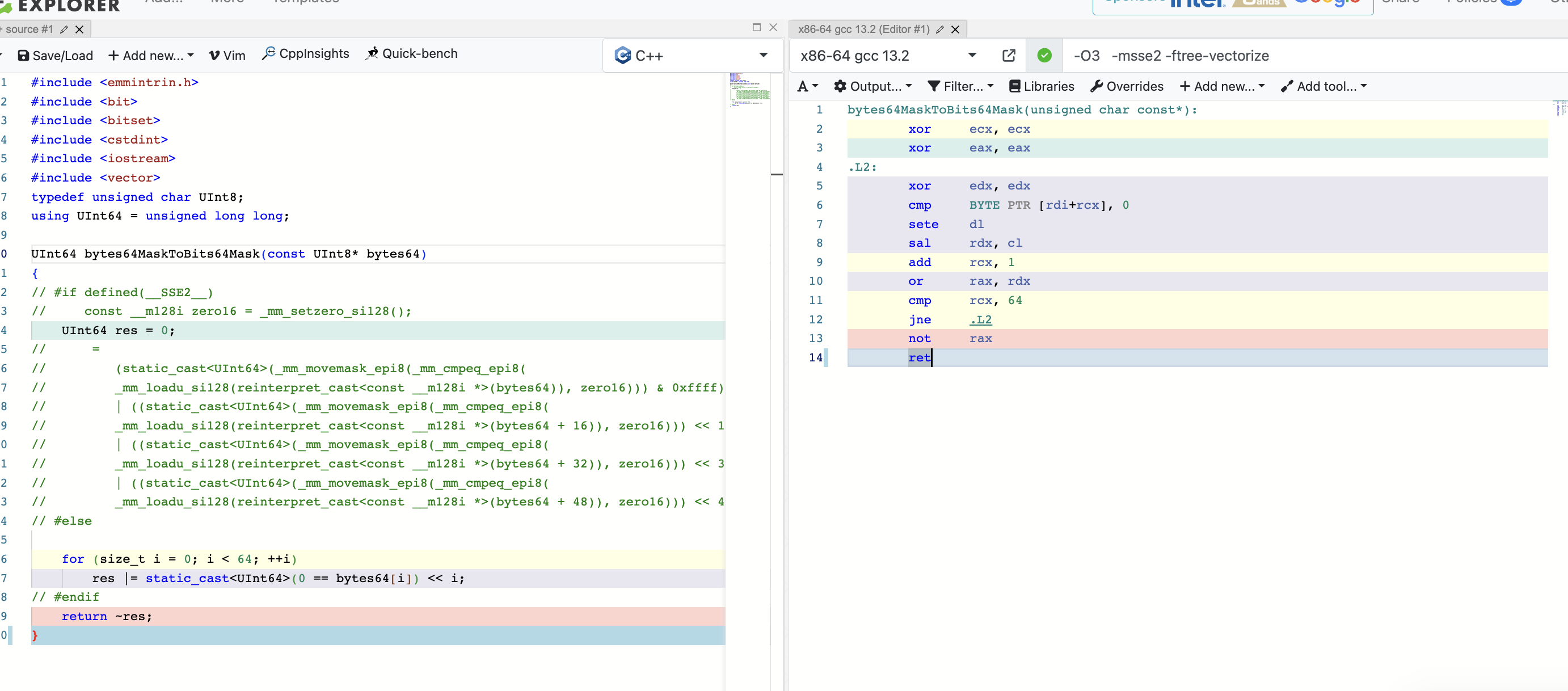
从微架构到向量化--CPU性能优化指北
引入 定位程序性能问题,相信大家都有很多很好的办法,比如用top/uptime观察负载和CPU使用率,用dstat/iostat观察io情况,ptrace/meminfo/vmstat观察内存、上下文切换和软硬中断等等,但是如果具体到CPU问题,我…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
