动态规划与0/1背包问题:深入解析
目录
一、动态规划简介
二、0/1背包问题概述
三、动态规划解决0/1背包问题
1. 定义子问题
2. 确定状态
3. 初始条件和边界情况
4. 计算最终结果
5. 代码实现
6. 空间优化
四、例题讲解
例题1:基础例题
例题2:路径恢复
例题3:扩展问题
五、总结
动态规划(Dynamic Programming, DP)是计算机科学中一种解决复杂问题的高效方法。通过将问题分解成更小的子问题并存储其结果,动态规划避免了重复计算,从而显著提高了效率。本文将详细介绍动态规划的基本概念,并以经典的0/1背包问题为例,展示如何应用动态规划进行求解。
一、动态规划简介
动态规划是一种优化技术,适用于解决具有重叠子问题和最优子结构性质的问题。其核心思想是通过记录已解决的子问题的结果,避免重复计算,从而提高算法效率。
动态规划的步骤通常包括:
- 定义子问题:将原问题分解为更小的子问题。
- 确定状态:定义表示子问题的状态变量。
- 状态转移方程:找到状态之间的递推关系。
- 初始条件和边界情况:设定初始状态的值。
- 计算最终结果:根据递推关系和初始条件计算出原问题的解。
二、0/1背包问题概述
0/1背包问题是组合优化中的经典问题之一,其定义如下:
给定一个容量为 W的背包,以及 n个物品,每个物品有一个重量 wi和价值 vi。在保证总重量不超过背包容量的前提下,如何选择物品使得总价值最大?
与之不同的是,每个物品只能选择一次(即0/1选择),而不是无限制地选择(完全背包问题)。
三、动态规划解决0/1背包问题
1. 定义子问题
设 dp[i][j]表示前 iii 个物品在背包容量为 jjj 时的最大总价值。目标是求 dp[n][W]。
2. 确定状态
状态 dp[i][j]dp[i][j]dp[i][j] 的值可以通过以下方式递推得到:
- 如果不选择第 i个物品,则 dp[i][j]=dp[i−1][j]dp[i][j] = dp[i-1][j]dp[i][j]=dp[i−1][j]。
- 如果选择第 i个物品,则 dp[i][j]=dp[i−1][j−wi]+vi,前提是j ≥ wi。
因此,状态转移方程为: dp[i][j]=max(dp[i−1][j],dp[i−1][j−wi]+vi)
3. 初始条件和边界情况
对于初始条件,当没有物品或背包容量为0时,总价值均为0:
dp[0][j] = 0 对于0≤j≤W
dp[i][0] = 0 对于0≤i≤n
4. 计算最终结果
通过自底向上填充DP表格,最终结果即为 dp[n][W]。
5. 代码实现
以下是C++实现,代码中包含了详细的解释:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int knapsack(const vector<int>& weights, const vector<int>& values, int W) {
int n = weights.size();
// 创建一个二维数组 dp,大小为 (n+1) x (W+1),并初始化为 0
vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));
// 填充 dp 表格
for (int i = 1; i <= n; ++i) {
for (int w = 0; w <= W; ++w) {
if (weights[i-1] <= w) {
// 如果可以放入当前物品,选择放或不放,取最大值
dp[i][w] = max(dp[i-1][w], dp[i-1][w - weights[i-1]] + values[i-1]);
} else {
// 如果不能放入当前物品,直接取前 i-1 个物品的最大值
dp[i][w] = dp[i-1][w];
}
}
}
// 最终结果是 dp[n][W],即考虑所有物品在最大重量 W 时的最大价值
return dp[n][W];
}
int main() {
vector<int> weights = {2, 3, 4, 5};
vector<int> values = {3, 4, 5, 6};
int W = 5;
cout << "Maximum value in Knapsack = " << knapsack(weights, values, W) << endl;
return 0;
}
6. 空间优化
上述实现的时间复杂度为 O(nW),空间复杂度同样为 O(nW)。可以通过空间优化将空间复杂度降至 O(W)。这是因为在计算 dp[i][j]时,只需要参考 dp[i−1][j]和 dp[i−1][j−wi] 两个状态,因此可以使用一维数组进行优化。
优化后的实现如下:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int knapsack_optimized(const vector<int>& weights, const vector<int>& values, int W) {
int n = weights.size();
vector<int> dp(W + 1, 0);
// 通过一维数组优化空间复杂度
for (int i = 0; i < n; ++i) {
for (int w = W; w >= weights[i]; --w) {
dp[w] = max(dp[w], dp[w - weights[i]] + values[i]);
}
}
return dp[W];
}
int main() {
vector<int> weights = {2, 3, 4, 5};
vector<int> values = {3, 4, 5, 6};
int W = 5;
cout << "Maximum value in Knapsack = " << knapsack_optimized(weights, values, W) << endl;
return 0;
}
四、例题讲解
例题1:基础例题
题目:给定一个背包的容量为 5,以及 4 个物品,每个物品的重量和价值分别为 {2, 3, 4, 5} 和 {3, 4, 5, 6}。求如何选择物品使得总价值最大。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int knapsack(const vector<int>& weights, const vector<int>& values, int W) {
int n = weights.size();
vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));
// 填充 dp 表格
for (int i = 1; i <= n; ++i) {
for (int w = 0; w <= W; ++w) {
if (weights[i-1] <= w) {
// 如果可以放入当前物品,选择放或不放,取最大值
dp[i][w] = max(dp[i-1][w], dp[i-1][w - weights[i-1]] + values[i-1]);
} else {
// 如果不能放入当前物品,直接取前 i-1 个物品的最大值
dp[i][w] = dp[i-1][w];
}
}
}
return dp[n][W];
}
int main() {
vector<int> weights = {2, 3, 4, 5};
vector<int> values = {3, 4, 5, 6};
int W = 5;
cout << "Maximum value in Knapsack = " << knapsack(weights, values, W) << endl;
return 0;
}
代码解释:
- 初始化
dp数组,用于存储子问题的解。 - 双重循环填充
dp表格,其中dp[i][w]表示前i个物品在容量为w时的最大价值。 - 根据物品是否放入背包来更新
dp[i][w]的值。 - 最后返回
dp[n][W],即为最大总价值。
例题2:路径恢复
题目:求解背包问题的同时,找出选择的物品。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
pair<int, vector<int>> knapsack_with_items(const vector<int>& weights, const vector<int>& values, int W) {
int n = weights.size();
vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));
vector<vector<bool>> keep(n + 1, vector<bool>(W + 1, false));
// 填充 dp 表格并记录是否选择物品
for (int i = 1; i <= n; ++i) {
for (int w = 0; w <= W; ++w) {
if (weights[i-1] <= w) {
if (dp[i-1][w] < dp[i-1][w - weights[i-1]] + values[i-1]) {
dp[i][w] = dp[i-1][w - weights[i-1]] + values[i-1];
keep[i][w] = true;
} else {
dp[i][w] = dp[i-1][w];
}
} else {
dp[i][w] = dp[i-1][w];
}
}
}
// 回溯找出选择的物品
int w = W;
vector<int> items;
for (int i = n; i >= 1; --i) {
if (keep[i][w]) {
items.push_back(i-1);
w -= weights[i-1];
}
}
return {dp[n][W], items};
}
int main() {
vector<int> weights = {2, 3, 4, 5};
vector<int> values = {3, 4, 5, 6};
int W = 5;
auto result = knapsack_with_items(weights, values, W);
cout << "Maximum value in Knapsack = " << result.first << endl;
cout << "Items included: ";
for (int i : result.second) {
cout << i << " ";
}
cout << endl;
return 0;
}
代码解释:
- 在
dp数组外增加一个keep数组,用于记录是否选择某个物品。 - 在填充
dp表格时,更新keep数组以记录选择情况。 - 通过回溯
keep数组,找出选择的物品并存储在items数组中。 - 最后返回最大总价值和选择的物品列表。
例题3:扩展问题
题目:考虑更多约束条件,如物品的体积和背包的体积限制。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Item {
int weight;
int volume;
int value;
};
int knapsack_with_volume(const vector<Item>& items, int W, int V) {
int n = items.size();
vector<vector<vector<int>>> dp(n + 1, vector<vector<int>>(W + 1, vector<int>(V + 1, 0)));
for (int i = 1; i <= n; ++i) {
for (int w = 0; w <= W; ++w) {
for (int v = 0; v <= V; ++v) {
if (items[i-1].weight <= w && items[i-1].volume <= v) {
dp[i][w][v] = max(dp[i-1][w][v], dp[i-1][w - items[i-1].weight][v - items[i-1].volume] + items[i-1].value);
} else {
dp[i][w][v] = dp[i-1][w][v];
}
}
}
}
return dp[n][W][V];
}
int main() {
vector<Item> items = {
{2, 3, 4},
{3, 4, 5},
{4, 5, 6},
{5, 6, 7}
};
int W = 5;
int V = 7;
cout << "Maximum value in Knapsack = " << knapsack_with_volume(items, W, V) << endl;
return 0;
}
代码解释:
- 定义
Item结构体,包含物品的重量、体积和价值。 - 初始化
dp三维数组,用于存储子问题的解。 - 三重循环填充
dp表格,其中dp[i][w][v]表示前i个物品在重量为w和体积为v时的最大价值。 - 根据物品是否放入背包来更新
dp[i][w][v]的值。 - 最后返回
dp[n][W][V],即为最大总价值。
五、总结
通过本文的详细解析和多个例题的讲解,我们可以深入理解动态规划及其在0/1背包问题中的应用。从定义子问题、确定状态、推导状态转移方程、设定初始条件,到计算最终结果,动态规划提供了一种系统而高效的解决问题的思路。
掌握动态规划的基本原理和应用技巧,不仅能解决背包问题,还能扩展到其他领域,如字符串匹配、序列比对、路径规划等。希望本文能够帮助读者更好地理解和应用动态规划,提升解决复杂问题的能力。
相关文章:

动态规划与0/1背包问题:深入解析
目录 一、动态规划简介 二、0/1背包问题概述 三、动态规划解决0/1背包问题 1. 定义子问题 2. 确定状态 3. 初始条件和边界情况 4. 计算最终结果 5. 代码实现 6. 空间优化 四、例题讲解 例题1:基础例题 例题2:路径恢复 例题3:扩展…...

Python爬虫:下载人生格言
Python爬虫:下载人生格言 爬取网页 将这些格言下载存储到本地 代码: import requests #导入requests库,用于提取网页 from lxml import etree#导入lxml库,用于Xpath数据解析#请求头 header{ user-agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) A…...

使用注意力机制的seq2seq
一、背景 1、机器翻译中,每个生成的词可能相关于源句子中不同的词,但是之前用的是最后一个RNN层出来的context。 2、加入注意力 (1)假设输入序列中有𝑇个词元, 解码时间步𝑡′的上下文变量是…...
我们的前端开发逆天了!1 小时搞定了新网站,还跟我说 “不要钱”
大家好,我是程序员鱼皮。前段时间我们上线了一个新软件 剪切助手 ,并且针对该项目做了一个官网: 很多同学表示官网很好看,还好奇是怎么做的,其实这个网站的背后还有个有趣的小故事。。。 鱼皮:我们要做个官…...

.NET 相关概念
.NET 和 .NET SDK .NET 介绍 .NET 是一个由 Microsoft 开发和维护的广泛用于构建各种类型应用程序的开发框架。它是一个跨平台、跨语言的开发平台,提供了丰富的类库、API和开发工具,支持开发者使用多种编程语言(如C#、VB.NET、F#等…...

Kubernetes 从集群中移除一个节点(Node)
目录 1. 移除工作节点(Worker Node)1.1 确定工作节点名称1.2 驱逐工作节点上的Pod1.3 删除工作节点1.4 重置该工作节点 2. 移除控制平面节点(Control Plane Node)2.1 确定控制平面节点名称2.2 驱逐控制平面节点上的Pod2.3 更新 etcd 集群2.4 从集群中删除控制平面节点2.5 重置移…...

高德地图离线版 使用高德地图api的方法
高德离线包我已经存至Gitee(自行下载即可):高德地图离线解决方案: 高德地图离线解决方案 然因为高德地图的瓦片地图太大,所以要让后端部署下 前端直接调用 如果本地 直接找到瓦片图路径就可以 initMap () {const base_url "…...

springboot 集成私有化Ollama大模型开源框架,搭建AI智能平台
Ollama是一个用于大数据和机器学习的平台,它可以帮助企业进行数据处理、分析和决策制定。 1、在Spring Boot项目pom.xml中添加Ollama客户端库依赖 <dependency><groupId>org.springframework.ai</groupId><artifactId>spring-a…...

6.key的层级结构
redis的key允许多个单词形成层级结构,多个单词之间用:隔开,格式如下: 项目名:业务名:类型:id 这个格式并非固定的,可以根据自己的需求来删除或添加词条。 例如: taobao:user:1 taobao:product:1 如果value是一个java对…...

LogonTracer图形化事件分析工具
LogonTracer这款工具是基于Python编写的,并使用Neo4j作为其数据库(Neo4j多用于图形数据库),是一款用于分析Windows安全事件登录日志的可视化工具。它会将登录相关事件中的主机名(或IP地址)和帐户名称关联起…...
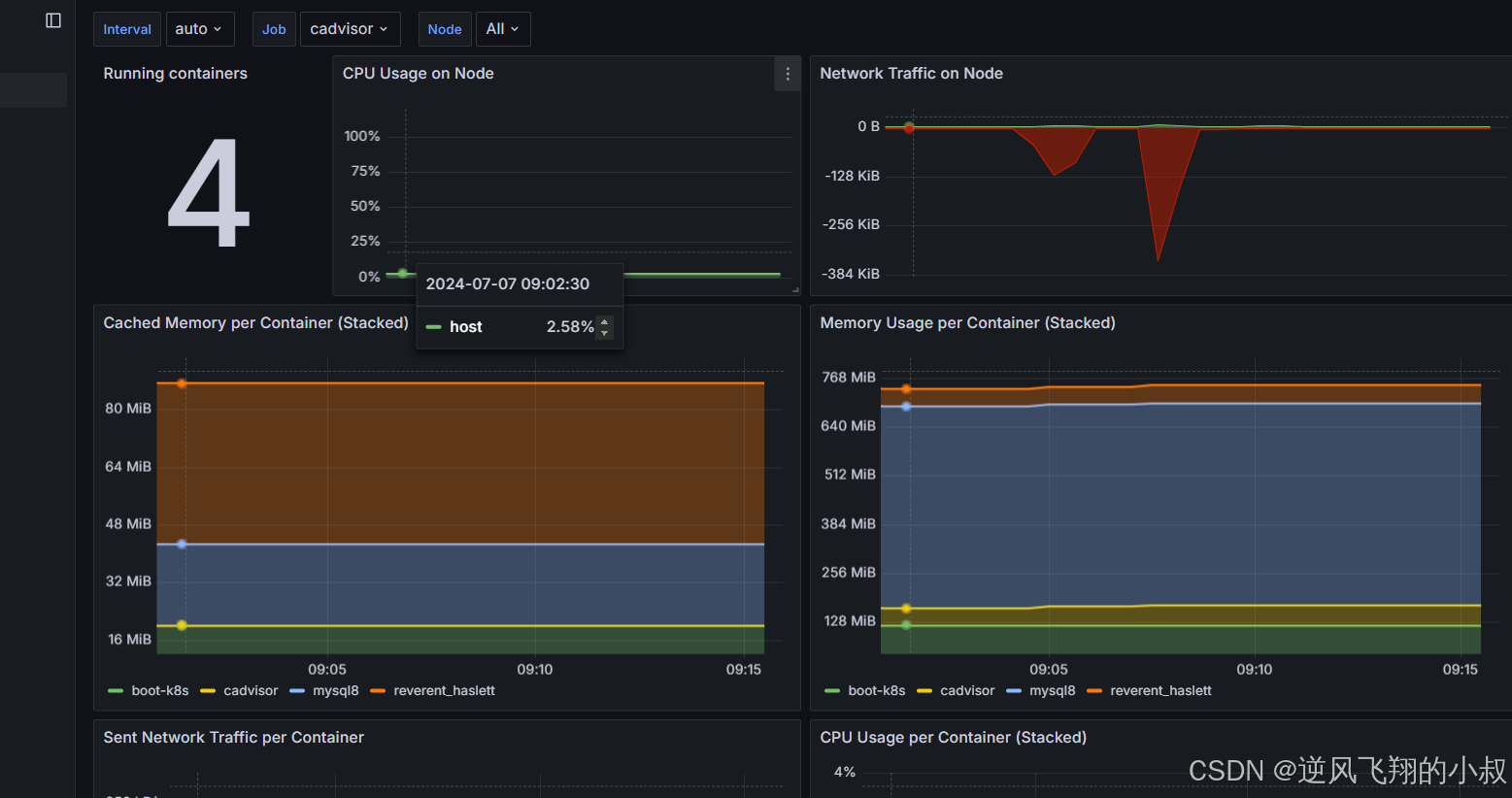
【云原生】Prometheus监控Docker指标并接入Grafana
目录 一、前言 二、docker监控概述 2.1 docker常用监控指标 2.2 docker常用监控工具 三、CAdvisor概述 3.1 CAdvisor是什么 3.2 CAdvisor功能特点 3.3 CAdvisor使用场景 四、CAdvisor对接Prometheus与Grafana 4.1 环境准备 4.2 docker部署CAdvisor 4.2.2 docker部署…...

搭建日志系统ELK(二)
搭建日志系统ELK(二) 架构设计 在搭建以ELK为核心的日志系统时,Logstash作为日志采集的核心组件,负责将各个服务的日志数据采集、清洗、过滤。然而缺点也很明显: 占用较多的服务器资源。配置复杂,学习曲线陡峭。处理大数据量时…...

常用排序算法的实现与介绍
常用排序算法的实现与介绍 在计算机科学中,排序算法是非常基础且重要的一类算法。本文将通过C语言代码实现,介绍几种常见的排序算法,包括冒泡排序、选择排序、插入排序和快速排序。以下是这些排序算法的具体实现和简要介绍。 1. 冒泡排序&am…...

仓颉语言 -- 宏
使用新版本 (2024-07-19 16:10发布的) 1、宏的简介 宏可以理解为一种特殊的函数。一般的函数在输入的值上进行计算,然后输出一个新的值,而宏的输入和输出都是程序本身。在输入一段程序(或程序片段,例如表达…...

Nginx代理minIO图片路径实现公网图片访问
1、网络部署情况 VUE前端项目Nginx部署在公司内网,端口7790 后台接口项目部署在公司内网,端口7022 minIO服务部署在公司内网,端口9000 公网IP设备将80端口映射到7790端口(具体映射方式不详),实现通过互…...
从零开始掌握tcpdump:参数详解
Linux tcpdump命令详解 1. 语法 tcpdump [-adeflnnNOpqStvxX] [-c <数据包数目>] [-dd] [-ddd] [-F <表达文件>] [-i <网络界面>] [-r <数据包文件>] [-s <数据包大小>] [-tt] [-T <数据包类型>] [-vv] [-w <数据包文件>] [输出数…...

漏洞挖掘 | edusrc记一次某中学小程序渗透测试
一、搜集渗透目标 现在的EDU挖web端的上分效率远不如小程序,因此这篇文章浅浅记录一次小程序的挖掘吧。如果各位大牛想要快速出洞,不妨跳过大学,学院等小程序,而重点关注小学、中学、幼儿园等,这些小程序的出洞率还是…...

vulhub:nginx解析漏洞CVE-2013-4547
此漏洞为文件名逻辑漏洞,该漏洞在上传图片时,修改其16进制编码可使其绕过策略,导致解析为 php。当Nginx 得到一个用户请求时,首先对 url 进行解析,进行正则匹配,如果匹配到以.php后缀结尾的文件名ÿ…...

备战秋招:2024游戏开发入行与跳槽面试详解
注意:以下为本次分享概要,视频版内容更全面深入,详见文末 1.游戏开发领域秋招准备与面试技巧 本次分享由优梦创客机构的创始人雷蒙德主讲,专注于2024年秋招期间游戏开发领域的入行与跳槽面试准备。本次分享重点在于提供面试技巧…...

红外热成像手持终端:从建筑检测到野外搜救的全方位应用
红外热成像手持终端,凭借其独特的红外探测与夜视功能,广泛应用于多个关键领域。无论是军事侦察、消防救援中的夜间作业,还是电力巡检、野生动物观察等多样场景,其精准的红外热成像技术均能提供至关重要的实时数据,助力…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
