[最短路Floyd],启动!!!
B3647 【模板】Floyd
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define PII pair<int,int >
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 405;
int n,m;
int dis[N][N];
void floyd()
{for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);}}}
}
int main()
{IOS;cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = 1e9;if(i==j) dis[i][j] = 0;}}while(m--){int a,b,w;cin>>a>>b>>w;dis[a][b] = min(dis[a][b],w);dis[b][a] = min(dis[b][a],w);//双向边}floyd(); for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cout<<dis[i][j]<<" ";}cout<<"\n";}
}P1744 采购特价商品
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define PII pair<int,int >
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 300;
int n,m;
double dis[300][300];
struct Node{int x;int y;
}va[N];
void flyod()
{for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);}}}
}
int main()
{
// IOS;cin>>n;for(int i=1;i<=n;i++) cin>>va[i].x>>va[i].y;cin>>m;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = 1e9;if(i==j) dis[i][j] = 0;}}for(int i=1;i<=m;i++){int a,b;cin>>a>>b;double w = sqrt( (va[a].x-va[b].x)*(va[a].x-va[b].x)+(va[a].y-va[b].y)*(va[a].y-va[b].y) );dis[a][b] = min(dis[a][b],w);dis[b][a] = min(dis[b][a],w);}flyod();int s,t;cin>>s>>t;printf("%.2lf",dis[s][t]);
}
P2888 [USACO07NOV] Cow Hurdles S
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define PII pair<int,int >
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 400;
int n,m,T;
int dis[N][N];
void floyd()
{for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = min(dis[i][j],max(dis[i][k],dis[k][j]));}}}
}
int main()
{IOS;cin>>n>>m>>T;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = 1e9;if(i==j) dis[i][j] = 0;} }while(m--){int a,b,w;cin>>a>>b>>w;dis[a][b] = min(dis[a][b],w);}floyd();while(T--){int a,b;cin>>a>>b;if(dis[a][b]==1e9) cout<<-1<<"\n";else cout<<dis[a][b]<<"\n";}
}P1364 医院设置
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define PII pair<int,int >
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 200;
int n;
int dis[N][N];
int va[N];
void floyd()
{for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);}}}
}
int main()
{IOS;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = 1e9; if(i==j) dis[i][j] =0;}}for(int i=1;i<=n;i++){int a,b;cin>>va[i]>>a>>b;if(b!=0) dis[i][b] = min(dis[i][b],1),dis[b][i] =min(dis[b][i],1);if(a!=0) dis[i][a] = min(dis[i][a],1),dis[a][i] = min(dis[a][i],1);}floyd();int minn =1e9;for(int i=1;i<=n;i++){int sum = 0;for(int j=1;j<=n;j++){sum += dis[i][j]*va[j];}minn = min(sum,minn);}cout<<minn;
}P1359 租用游艇
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define PII pair<int,int >
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const int N = 400;
int n,m;
int dis[N][N];
void floyd()
{for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);}}}
}
int main()
{IOS;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j] = 1e9;if(i==j) dis[i][j] = 0;}}for(int i=1;i<=n-1;i++){for(int j=i+1;j<=n;j++){int w;cin>>w;dis[i][j] = min(dis[i][j],w);}}floyd();cout<<dis[1][n];
}相关文章:

[最短路Floyd],启动!!!
B3647 【模板】Floyd #include<bits/stdc.h> #define ll long long #define fi first #define se second #define pb push_back #define PII pair<int,int > #define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0) using namespace std; const int N …...
7月29(信息差)
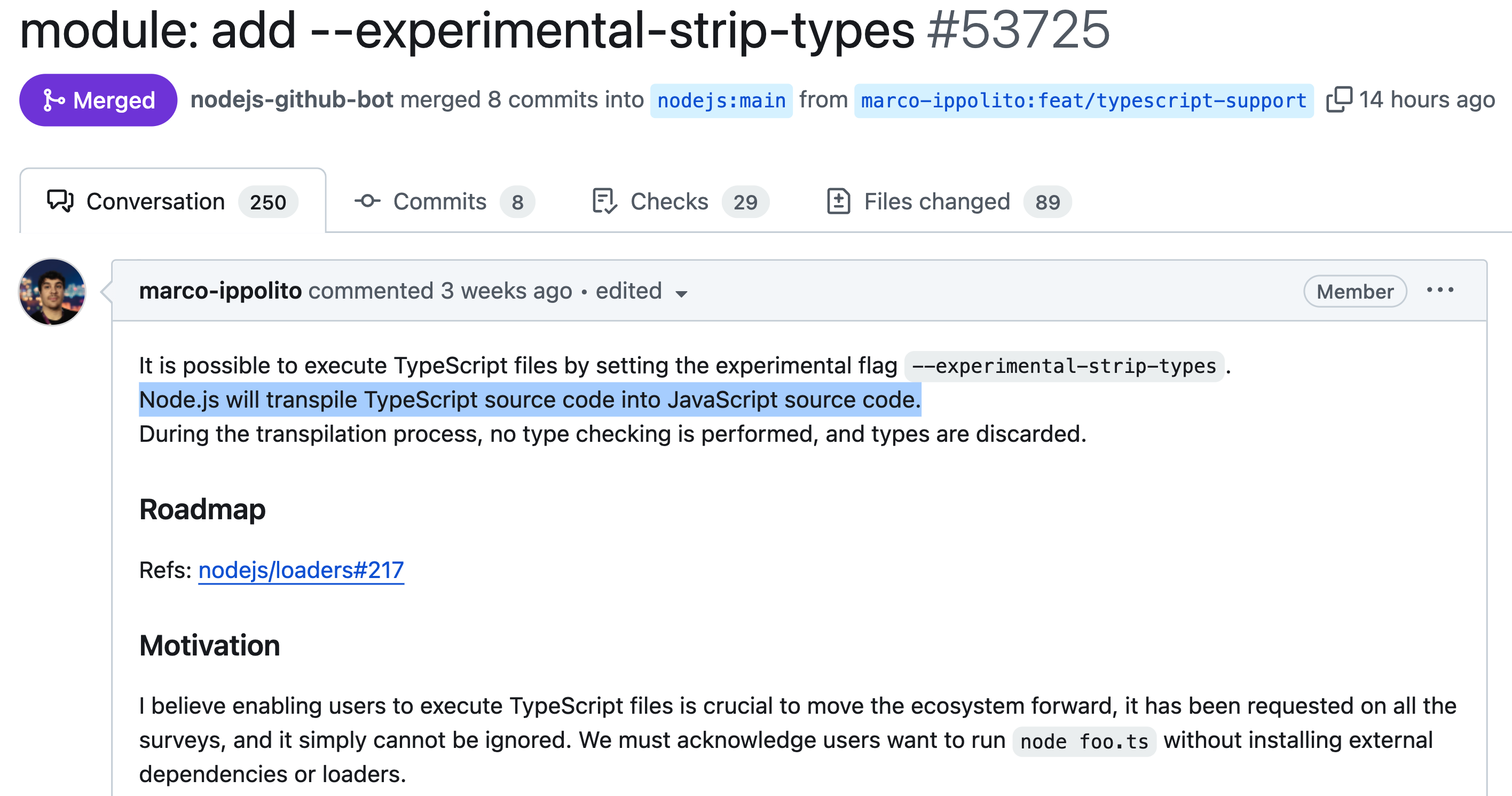
🌍最强模型 Llama 3.1 如期而至!扎克伯格最新访谈:Llama 会成为 AI 界的 Linux 🎄谷歌AlphaProof攻克国际奥赛数学题 https://www.51cto.com/article/793632.html ✨SearchGPT第一波评测来了!响应速度超快还没广告&…...

ubuntu中禁止使用鼠标拖动来移动文件
windows和ubuntu中都可以拖动文件到其他路径,然后达到移动文件的目的。 这种方式有好处也有坏处,好处是移动文件方便了,坏处是误操作后会造成故障,尤其是ubuntu中,本身鼠标就特别灵敏并且操作不便,拖动一个…...

【密码学】椭圆曲线密码体制(ECC)
椭圆曲线密码体制(Elliptic Curve Cryptography, ECC)是一种基于椭圆曲线数学特性的公钥密码系统。在介绍椭圆曲线之前,我们先来了解一下椭圆曲线的基本概念。 一、椭圆曲线是什么? (1)椭圆曲线的数学定义…...
第25集《大佛顶首楞严经》
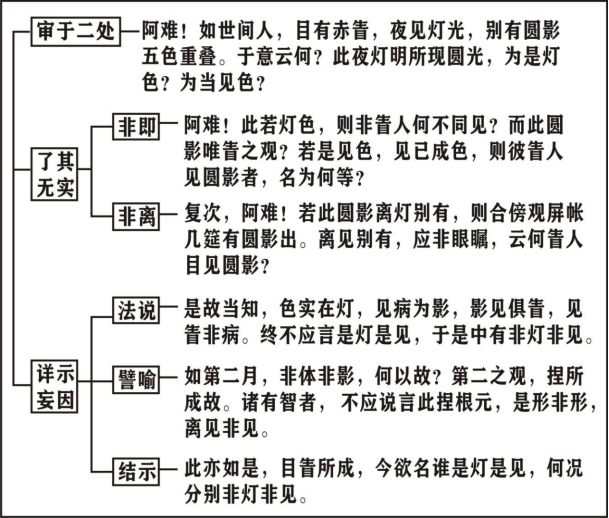
丑二、腾疑细释 分二:寅一、阿难腾疑;寅二、如来细释 请大家打开讲义第五十六页,“丑二、腾疑细释”。 本经的修学重点,就是修学首楞严王三昧。它的整个重点,其实就是一个心地法门。我们在行菩萨道的时候慢慢会发觉…...
 详细解析)
python 读写文件之 open 和 with open() 详细解析
python 读写文件之 open 和 with open() 详细解析 文章目录 python 读写文件之 open 和 with open() 详细解析1. open() 和 with open() 能打开不同的文件类型吗?2. 文本文件和二进制文件的区别2.1 文本文件 (Text Files)2.2 二进制文件 (Binary Files)区别 3. 读文…...

操作系统:内存----知识点
什么是虚拟内存? 虚拟内存简称虚存,是计算机系统内存管理的一种技术。它是相对于物理内存而言的,可以理解为“假的”内存。它使得应用程序认为它拥有连续可用的内存(一个连续完整的地址空间),允许程序员编…...

pfx如何配置到nginx中
有pfx文件的时候如何在nginx上使用 好的,如果您已经确认没有中间证书(或中间证书内容为空),那么可以直接使用服务器证书和私钥。以下是简化后的步骤: 从PFX文件中导出私钥: openssl pkcs12 -in xxx.com.pfx…...
详细测评下搬瓦工香港CN2 GIA VPS
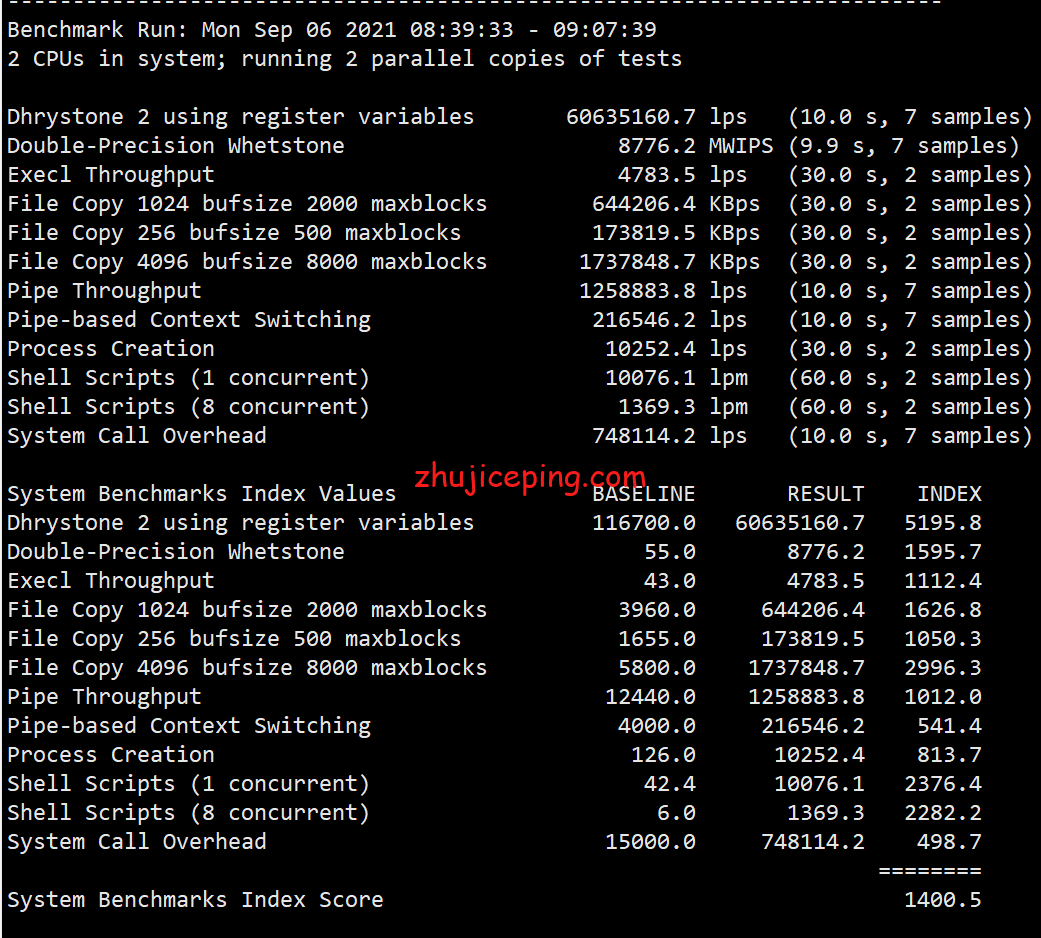
搬瓦工香港VPS分移动CMI和电信CN2 GIA两个大类,一个属于骨干网,一个属于轻负载。搬瓦工的香港CN2 GIA根据测试来看实际上是CN2 GIABGP,并非三网纯CN2 GIA。详细测评数据如下: 用FIO再给测试一下硬盘I/O,可以仔细看看数…...

Java中的五种线程池类型
Java中的五种线程池类型 1. CachedThreadPool (有缓冲的线程池)2. FixedThreadPool (固定大小的线程池)3. ScheduledThreadPool(计划线程池)4. SingleThreadExecutor (单线程线程池)…...

FFmpeg Windows安装教程
一. 下载ffmpeg 进入Download FFmpeg网址,点击下载windows版ffmpeg。 下载第一个essentials版本就行。 二. 环境配置 上面源码解压后如下 将bin添加到系统环境变量 验证安装是否成功,输入ffmpeg –version,显示版本即为安装成功。...

‘#‘ is not followed by a macro parameter 关于宏定义的错误
今天在项目代码上想定义一个这样的宏,结果编译错误,这个宏定义类似这样的: #define DELETE_FILE_DPP(key) \ #ifdef PLATFORM_DPP \delete_file(&key); \ #endif 因为有平台之分需要用到编译宏,但不想每个调用的地方都写 #i…...

内网穿透--meterpreter端口转发实验
实验背景 通过公司带有防火墙功能的路由器接入互联网,然后由于私网IP的缘故,公网无法直接访问内部主机,则需要通过已连接会话,代理穿透访问内网主机服务。 实验设备 1.路由器一台 2.内网 Win 7一台 3.公网 Kali 一台 4.网络 …...

Python 数据类:减少样板并提高可读性
一.介绍 在本文中,我们将了解数据类。Python 3.7 引入了数据类,这是一个强大的功能,它简化了创建主要用于存储数据的类的过程。数据类减少了样板代码并提供有用的默认行为,使您的代码更简洁、更高效。 二.为什么要使用数据类&am…...

家庭教育系列—北京海淀区”鸡娃“攻略
文章目录 1. 背景介绍2. 道3. 法3.1 **目标设定(Goal Setting)**3.2 **学习计划(Study Planning)**3.3 **资源利用(Resource Utilization)**3.4 **能力培养(Skill Development)**4. 术4.1 英语4.1.1 启蒙4.1.2 启蒙之后4.3 数学4.3.1 奥数4.3.2 普通数学知识4.4 语文4.…...
)
DLMS/COSEM中的信息安全:DLMS/COSEM安全概念(下)
3.安全语境 安全语境定义了与加密转换有关的安全属性,并包括以下元素: ——安全组件,确定可用的安全算法。 ——安全策略,在AA内对所有xDLMS APDU确定将应用的那种保护; ——与给定的安全算法相关的安全资料,包含安全密钥、初始化向量、公共密钥证书等。由于安全资料是针…...

基于 systemc-2.3.1的virtual device 接入 qemu-arm
1,下载systemc-2.3.1 下载网址: SystemC Files $ wget https://www.accellera.org/images/downloads/standards/systemc/systemc-2.3.1.tgz 2,编译安装 systemc-2.3.1 tar zxf systemc-2.3.1.tgz cd systemc-2.3.1/ export CXXg mkdir bu…...
自动化测试)
(七)自动化测试
1. 简述什么是UI自动化测试? 正确回答通过率:78.0%[ 详情 ] 推荐指数: ★★★★ 试题难度: 中级 UI自动化测试(User Interface Automation Testing)是一种通过编写脚本或使用自动化测试工具,对用户界面(UI)进行自动化测试的方法。它可以模拟用户与应用程序或网站的交…...
【信创】virtualbox内虚拟机连接U盘 _ 统信 _ 麒麟 _ 中科方德
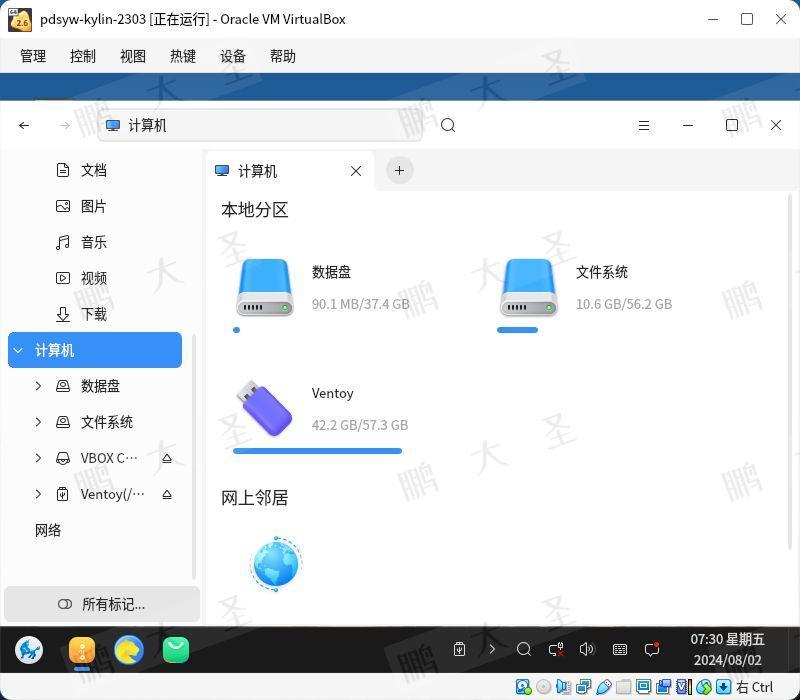
原文链接:【信创】virtualbox内虚拟机连接U盘 | 统信 | 麒麟 | 中科方德 Hello,大家好啊!今天给大家带来一篇关于在信创操作系统上使用VirtualBox虚拟机连接物理主机U盘的文章。在使用VirtualBox虚拟机时,有时候需要将物理主机上的…...

【2024】Datawhale AI夏令营 Task4笔记——vllm加速方式修改及llm推理参数调整上分
【2024】Datawhale AI夏令营 Task4笔记——vllm加速方式修改及llm推理参数调整上分 本文承接文章【2024】Datawhale AI夏令营 Task3笔记——Baseline2部分代码解读及初步上分思路,对其中vllm加速方式进行修改,推理速度获得了极大提升。另外,…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
