二维凸包算法 Julia实现
问题描述:给定平面上 n n n 个点的集合 Q Q Q,求其子集 P P P 构成 Q Q Q 的凸包,即 ∀ p ∈ Q , ∃ p 0 , p 1 , p 2 ∈ P \forall p \in Q, \exist p_0, p_1, p_2 \in P ∀p∈Q,∃p0,p1,p2∈P 使得点 p p p 在以点 p 0 , p 1 , p 2 p_0, p_1, p_2 p0,p1,p2 构成的三角形中或边上。
朴素枚举
初始设 P : = Q P := Q P:=Q,枚举 p 0 , p 1 , p 2 , p p_0, p_1, p_2, p p0,p1,p2,p,判断 p p p 是否在以点 p 0 , p 1 , p 2 p_0, p_1, p_2 p0,p1,p2 构成的三角形中,是则删去 p p p,最后剩下的即为凸包。注意到纵坐标最小的点必在结果中,可将 p 0 p_0 p0 固定为之。
算法时间复杂度 O ( n 3 ) O(n^3) O(n3)。代码:
cross(p, q) = p[1] * q[2] - q[1] * p[2]function NE(Q)function inΔ(p0, p1, p2, p)v0, v1, v2 = p .- p0, p1 .- p0, p2 .- p0c0, c1, c2 = cross(v1, v2), cross(v0, v1), cross(v0, v2)return c0 * c1 < 0 && c0 * c2 > 0 && abs(c2 - c1) < abs(c0)endm = argmin(last.(Q))p0, Q = Q[m], vcat(Q[begin : m - 1], Q[m + 1 : end])for i = length(Q) : -1 : 1f = falsefor j = 2 : length(Q)if i == j continue endfor k = 1 : j - 1if i == k continue endif inΔ(p0, Q[j], Q[k], Q[i])f = true; breakendendif f break endendif fdeleteat!(Q, i)endendsort!(Q, lt = (p, q) -> cross(p .- p0, q .- p0) > 0)return vcat(p0, Q)
end
Jarvis March 算法
按逆时针对 P P P 排序,将问题转化成已知 p 0 , p 1 , . . . , p k p_0, p_1, ..., p_k p0,p1,...,pk 如何求 p k + 1 p_{k+1} pk+1。
p 0 p_0 p0 固定为纵坐标最小的点。此时 Q − { p k } Q - \{p_k\} Q−{pk} 中所有点都在向量 p k − p k − 1 p_k - p_{k-1} pk−pk−1 的左侧,即向量集 { p − p k ∣ p ∈ Q − { p k } } \{ p - p_k | p \in Q - \{ p_k \} \} {p−pk∣p∈Q−{pk}} 可在叉积运算的正负性上构成偏序集,最右的向量即为 p k + 1 − p k p_{k+1} - p_k pk+1−pk。当 p k + 1 = p 0 p_{k+1} = p_0 pk+1=p0 时算法终止。
时间复杂度 O ( n h ) O(nh) O(nh), h h h 为凸包的点数。代码:
function Jarvis(Q)function march(A, cmp)r = A[begin]for i in A[2 : end]if cmp(i, r)r = iendendreturn rendP = [march(Q, (p, q) -> last(p) < last(q))]while trueq = march(Q, (p, q) -> cross(p .- P[end], q .- P[end]) > 0)if P[begin] == qbreakendpush!(P, q)endreturn P
end
Graham Scan 算法
p 0 p_0 p0 固定为纵坐标最小的点。按与 p 0 p_0 p0 构成向量的极角序对 Q Q Q 排序,将问题转化为已知 Q Q Q 中前 k k k 个点的闭包 P k P_k Pk,如何求 Q Q Q 中前 k + 1 k + 1 k+1 个点的闭包 P k + 1 P_{k+1} Pk+1。
不妨设 P k = { p 0 , p 1 , . . , p k } P_k = \{ p_0, p_1, .., p_k \} Pk={p0,p1,..,pk},注意到 p k + 1 p_{k+1} pk+1 的在 p k − p 0 p_k - p_0 pk−p0 的左边,而 P k P_k Pk 中其它点在 p k − p 0 p_k - p_0 pk−p0 的右边,故一定有 p k + 1 ∈ P k + 1 p_{k+1} \in P_{k+1} pk+1∈Pk+1,设 P k + 1 = P k + { p k + 1 } P_{k+1} = P_k + \{ p_{k+1} \} Pk+1=Pk+{pk+1}。判断 p k + 1 p_{k+1} pk+1 在 p k − p k − 1 p_k - p_{k-1} pk−pk−1 的哪边,若在右边则从凸包 P k + 1 P_{k+1} Pk+1 中抛出 p k p_k pk,继续迭代判断 p k + 1 p_{k+1} pk+1 在 p k − 1 − p k − 2 p_{k-1} - p_{k-2} pk−1−pk−2 的哪边,直到在左边则结束迭代,最后剩下的即为凸包 P k + 1 P_{k+1} Pk+1。
用栈存储中间过程的凸包计算, Q Q Q 中每个点仅会进出栈一次,故扫描为线性时间,主要耗时在排序。时间复杂度 O ( n log n ) O(n \log n) O(nlogn)。代码:
function GrahamScan(Q)P = Q[1 : 3]for q in Q[4 : end]while cross(q .- P[end], P[end] .- P[end - 1]) > 0pop!(P)endpush!(P, q)endreturn P
endfunction Graham(Q)m = argmin(last.(Q))p0, Q = Q[m], vcat(Q[begin : m - 1], Q[m + 1 : end])Q = sort(Q, lt = (p, q) -> cross(p .- p0, q .- p0) > 0)return GrahamScan(vcat(p0, Q))
end
分治算法
将当前点集均分为左右两部分,分别用分治算法得到各自的凸包,再将两个凸包合并成一个凸包。
合并过程是,取一边凸包上某一点作为基点,求另一边凸包上极角最大和最小的点,则一边凸包的点按基点的极角序有序,另一边凸包的点分为两条从极角最小到极角最大的极角序有序点集,将三个极角序有序点集按三路归并成一个极角序有序的点集,并进行 Graham Scan 算法流程。
时间函数 T ( n ) = T ( n 2 ) + O ( n ) T(n) = T(\frac{n}{2}) + O(n) T(n)=T(2n)+O(n),得时间复杂度 O ( n log n ) O(n \log n) O(nlogn),但常数很大。代码:
function DC(Q)function argMaxMin(A, cmp)u, v = 1, 1for i = 2 : length(A)if cmp(A[i], A[u]) > 0u = iendif cmp(A[i], A[v]) < 0v = iendendreturn u, vendfunction merge3(A, B, C, cmp)ia, ib, ic = length(A), length(B), length(C)fa, fb, fc, R::typeof(A) = ia > 0, ib > 0, ic > 0, []while fa || fb || fcif fa && (!fb || cmp(A[ia], B[ib]) < 0) && (!fc || cmp(A[ia], C[ic]) < 0)push!(R, A[ia]); ia -= 1; fa = ia > 0elseif fb && (!fc || cmp(B[ib], C[ic]) < 0)push!(R, B[ib]); ib -= 1; fb = ib > 0elsepush!(R, C[ic]); ic -= 1; fc = ic > 0endendreturn reverse(R)endfunction CH(Q)if length(Q) <= 3m = argmin(last.(Q))p0, Q = Q[m], vcat(Q[begin : m - 1], Q[m + 1 : end])if length(Q) == 2 && cross(Q[1] .- p0, Q[2] .- p0) < 0Q = reverse(Q)endreturn vcat(p0, Q)endm = length(Q) ÷ 2L, R = CH(Q[begin : m]), CH(Q[m + 1 : end])if L[1][2] > R[1][2]L, R = R, Lendp0, L = L[1], L[2 : end]u, v = argMaxMin(R, (p, q) -> cross(p .- p0, q .- p0))slice(A, l, r) = l <= r ? A[l : r] : vcat(A[l : end], A[begin : r])R0, R1 = slice(R, u, v), slice(R, v, u)[end - 1 : -1 : begin + 1]return GrahamScan(vcat(p0, merge3(L, R0, R1, (p, q) -> cross(p .- p0, q .- p0))))endQ = sort(Q, by = first)return CH(Q)
end
实验测试
随机在 { ( x , y ) ∣ 0 ≤ x , y < 100 } \{ (x, y) | 0 ≤ x, y < 100 \} {(x,y)∣0≤x,y<100} 区域生成 3000 个点,测试各算法凸包结果和效率。代码:
using Random
function genData(n)Random.seed!(2024)return [q for q in zip(100 * rand(n), 100 * rand(n))]
end
Q = genData(3000)
@time P1 = NE(Q)
@time P2 = Jarvis(Q)
@time P3 = Graham(Q)
@time P4 = DC(Q)
@show length(P1)
@show length(P2), P2 == P1
@show length(P3), P3 == P1
@show length(P4), P4 == P1
结果:
0.684359 seconds (585.47 k allocations: 40.423 MiB, 8.73% gc time, 53.56% compilation time)0.047316 seconds (27.23 k allocations: 2.719 MiB, 97.94% compilation time)0.175105 seconds (142.39 k allocations: 9.483 MiB, 3.61% gc time, 96.17% compilation time)0.412407 seconds (423.40 k allocations: 25.049 MiB, 98.20% compilation time)
length(P1) = 19
(length(P2), P2 == P1) = (19, true)
(length(P3), P3 == P1) = (19, true)
(length(P4), P4 == P1) = (19, true)
相关文章:

二维凸包算法 Julia实现
问题描述:给定平面上 n n n 个点的集合 Q Q Q,求其子集 P P P 构成 Q Q Q 的凸包,即 ∀ p ∈ Q , ∃ p 0 , p 1 , p 2 ∈ P \forall p \in Q, \exist p_0, p_1, p_2 \in P ∀p∈Q,∃p0,p1,p2∈P 使得点 p p p 在以点 p 0 , p 1 …...
python dash框架
Dash 是一个用于创建数据分析型 web 应用的 Python 框架。它由 Plotly 团队开发,并且可以用来构建交互式的 web 应用程序,这些应用能够包含图表、表格、地图等多种数据可视化组件。 Dash 的特点: 易于使用:Dash 使用 Python 语法…...

2.外部中断(EXTI)
理论 NVIC:嵌套向量中断控制器(解释教程) 外部通用中断线(EXTI0~EXTI15):每个GPIO设置成中断模式,与中断控制器连接的线 外部中断触发方式 上升沿触发、下降沿触发、双边沿触发 外部中断触发函数 在stm32f1xx_it.c文件…...

Python | SyntaxError: invalid syntax 深度解析
Python | SyntaxError: invalid syntax 深度解析 在Python编程中,SyntaxError: invalid syntax是一个常见的错误,它表明Python解释器在尝试解析代码时遇到了语法问题。这个错误通常是由于代码中存在拼写错误、缺少符号(如括号、冒号或逗号&a…...
付费进群系统源码原版最新修复全开源版
付费进群,和平时所见到的别人拉你进群是不一样的,付费进群需要先缴费以后,才会看到群的二维码,扫码进群或者是长按二维码图片识别进群,付费进群这个功能广泛应用于拼多多的砍价群,活动的助力群,…...

Docker容器部署的SpringBoot项目jar包,上传文件但是找不到路径的问题
在docker容器内部署的jar包运行后,请求访问都没有问题,在文件上传时,发现上传图片接口响应成功,但是图片路径报404错误,发现找不到路径。 在服务器上查看也没有找到相关图片。 原因: 启动docker镜像时没…...
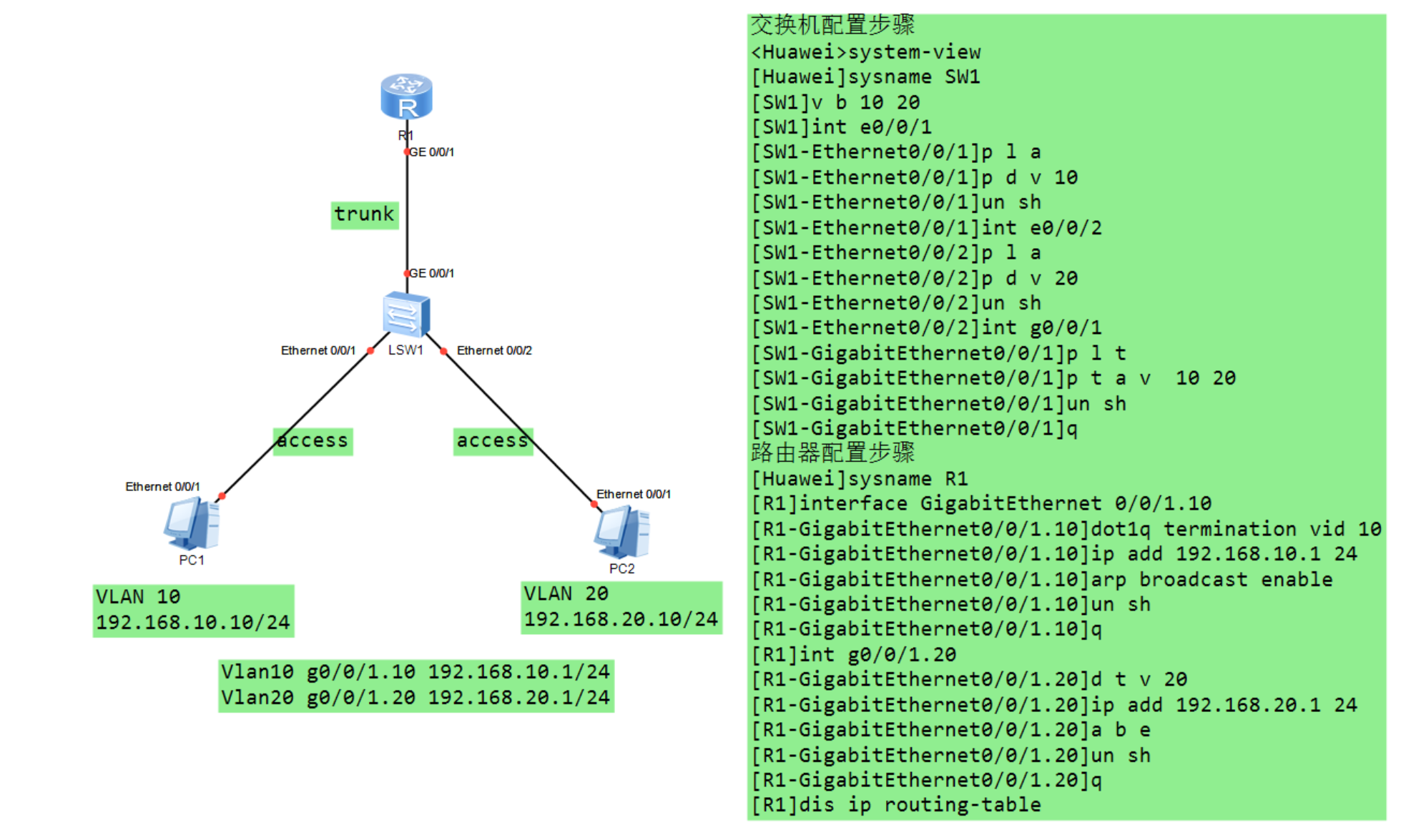
云计算学习——5G网络技术
系列文章目录 提示:仅用于个人学习,进行查漏补缺使用。 Day1 网络参考模型 Day2 网络综合布线与应用 Day3 IP地址 Day4 华为eNSP网络设备模拟器的基础安装及简单使用 Day5 交换机的基本原理与配置 Day6 路由器的原理与配置 Day7 网络层协议介绍一 Day8 传…...

matlab仿真 信道编码和交织(上)
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第八章内容,有兴趣的读者请阅读原书) clear all N10;%信息比特的行数 n7;%hamming码组长度n2^m-1 m3;%监督位长度 [H,G]hammgen(m);%产生(n,n-…...

基于YOLOv8的高压输电线路异物检测系统
基于YOLOv8的高压输电线路异物检测系统 (价格88) 包含 【“鸟窝”,“风筝”,“气球”,“垃圾”】 4个类 通过PYQT构建UI界面,包含图片检测,视频检测,摄像头实时检测。 (该系统可以根据数…...

23款奔驰GLS450加装原厂电吸门配置,提升车辆舒适性和便利性
今天是一台22款奔驰GLS450,车主是佛山的 以前被不良商家坑了 装了副厂的电吸门 刚开始就很正常 用了半年之后 就开始开不了门,被锁在里面,刚开始车主以为是零件坏了 后来越来越频繁,本来是为了家里老人小孩关门方便而升级的&#…...

git操作流程笔记
1、在本地项目文件夹右击鼠标点击Git Bash Here 2、输入git init,这个目录变成git可以管理的仓库,会出现一个.git文件夹,如果没出现的话需要选择“显示隐藏文件”(不会的同学自行百度一下) 3、绑定本地仓库与远程仓库…...

【QT】常用控件-上
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 目录 👉🏻QWidgetenabledgeometryrect制作上下左右按钮 window frame 的影响window titlewindowIcon代码示例: 通过 qrc 管理图片作为图标 windowOpacitycursor使用qrc自…...
帮助网站提升用户参与度的5个WordPress插件
仅靠编写精彩的内容、设计精美的图像和创建简化的客户旅程不足以提高网站参与度。您需要让用户在首次访问后继续与您的网站互动并成为回访者,才能真正吸引您所追求的兴趣。 幸运的是,对于 WordPress 用户来说,有数百种工具可用于提高用户参与…...

理解 Python 中的 @wraps:保留函数元数据
一.介绍 在本文中,我们将了解 wraps。在 Python 中使用装饰器时,您可能会遇到原始函数的元数据丢失的情况。这时,functools 模块中的 wraps 装饰器就可以派上用场了。让我们深入了解 wraps 的作用及其重要性。 二.简单装饰器的问题 首先&a…...
cjson
文章目录 概述编译cjson_test 小结 概述 在网络传输中,网络数据序列化,常用的有那么几种,json,protobuf都是很常用的,这一篇来写下json。 Json常用的有几个,rapidjson,jsoncpp,还有…...

Docker data root 目录更改
有时候受限于系统根目录空间的限制,需要将 docker data root 目录更改为其它目录,如单独挂载一个磁盘或存储。本篇文章介绍如何操作。 修改docker 工作目录 修改配置文件/etc/docker/daemon.json(在19.x 版本之前使用grapth) {&q…...
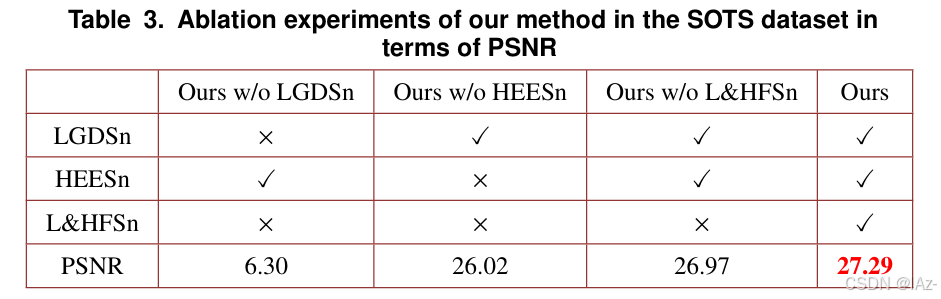
[CR]厚云填补_SEGDNet
Structure-transferring edge-enhanced grid dehazing network Abstract 在过去的二十年里,图像去雾问题在计算机视觉界受到了极大的关注。在雾霾条件下,由于空气中水汽和粉尘颗粒的散射,图像的清晰度严重降低,使得许多计算机视觉…...
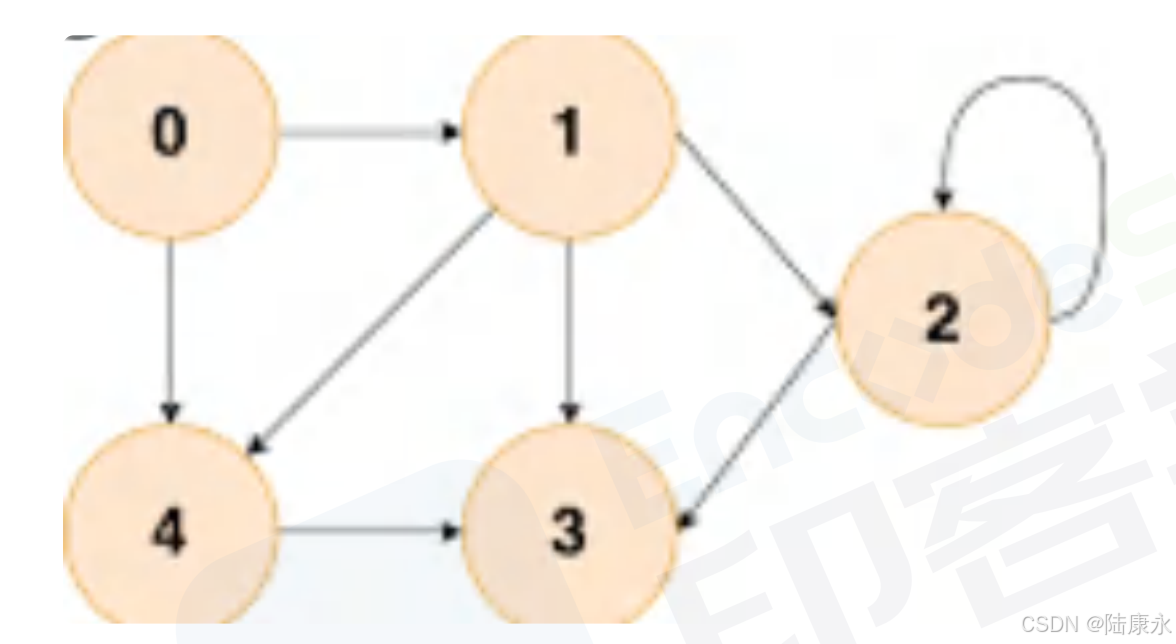
图-基础概念
是什么 图是一种抽象的数据类型,在图中的数据元素通常称作节点,V是所以定点的集合,E是所有边的集合 图的分类 有向图 如果两个订单v,w,只能由v向w,而不能w向v,那么我们就把何种情况叫做一个从…...

Javascript前端基础面试(十)
MVVM Vue MVVM这一篇就够啦!_vue r mvvm-CSDN博客 点容器内的图标,图标边框变成border 1px solid red,点空白处重置 <div id"container"> <img src"icon.png" alt"Icon" class"icon"> <!…...
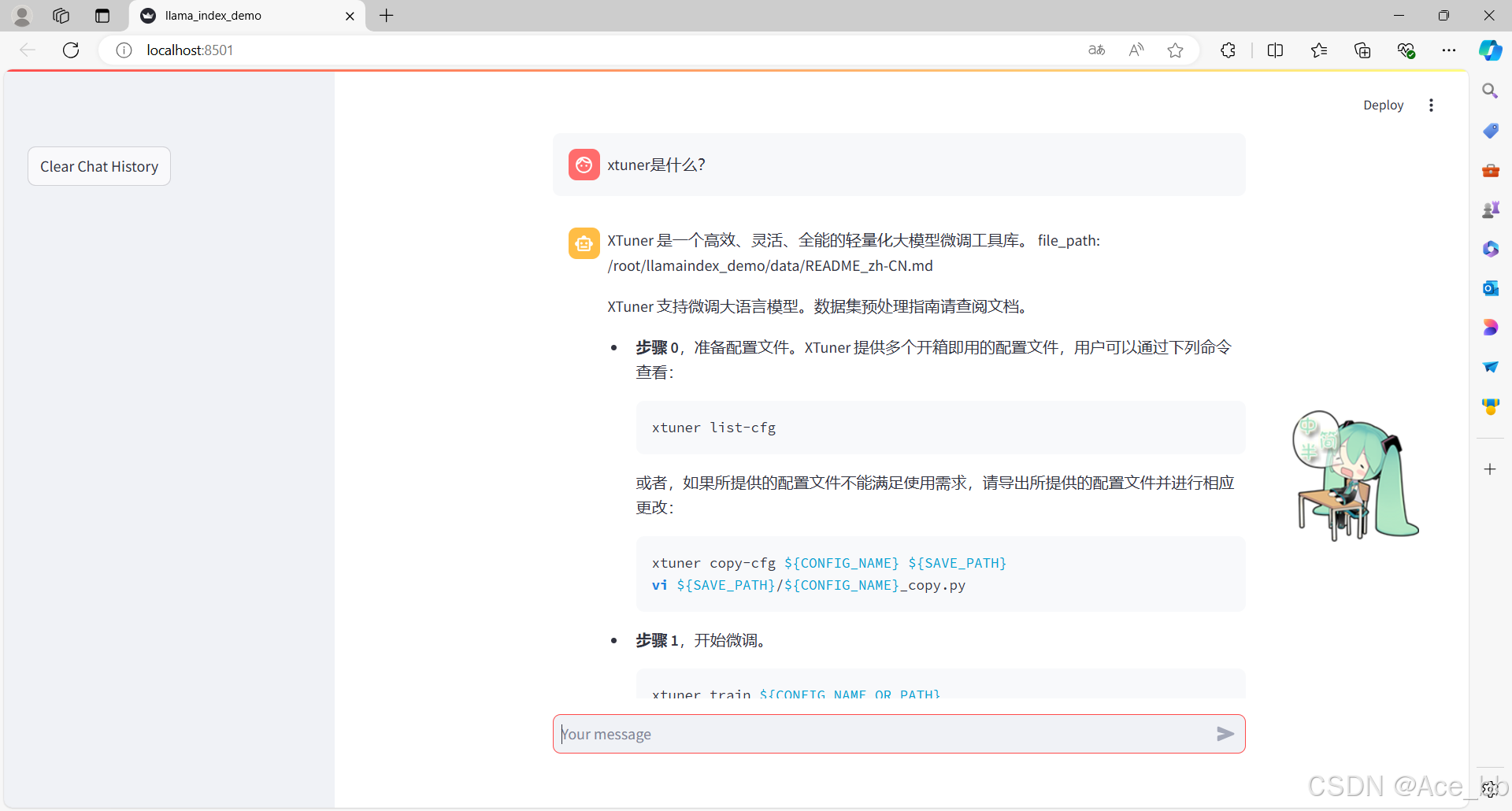
书生大模型实战营闯关记录----第五关:LlamaIndex+Internlm2 RAG实践Demo:效果对比,文档加载,向量库构建,检索器,模型推理
文章目录 1. 前置知识RAG背景RAG 效果比对 2. 环境、模型准备2.1 配置基础环境2.2 安装 Python环境和依赖包2.3 下载 Sentence Transformer 模型2.4 下载 NLTK 相关资源 3. LlamaIndex HuggingFaceLLM4. LlamaIndex RAG加载文档构建向量存储索引库检索器RAG代码 5. LlamaIndex …...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
