图-基础概念
是什么
图是一种抽象的数据类型,在图中的数据元素通常称作节点,V是所以定点的集合,E是所有边的集合
图的分类
有向图
如果两个订单v,w,只能由v向w,而不能w向v,那么我们就把何种情况叫做一个从v到w的有向边。v也被陈作初始点,w也被称为终点。这种图也被称为有向图
无向图
如果v和w是没有顺序的,从v到达w和从w到达v是完全相同的,这种图就叫做无向图
常见的图表达方式
邻接矩阵
通过一个二维数组G[N][N]表示N个点到N-1编号,通过邻街矩阵可以立即看到两个订单直接是否存在一条边

邻接表
存储方式如下

在javascript中永Object进行表示
const graph = {A: [2, 3, 5],B: [2],C: [0, 1, 3],D: [0, 2],E: [6],F: [0, 6],G: [4, 5]
}用数组进行表示
代码A
const graph = {0: [1, 4],1: [2, 4],2: [2, 3],3: [],4: [3], }常见的操作方式
深度优先遍历
广度优先遍历
数据如上面的代码A
深度优先
const visited = new Set()
const dfs = (n) => {console.log(n)visited.add(n) // graph[n].forEach(c => {if(!visited.has(c)){ //demo,第一次,遍历graph下的graph[1]和graph[4]dfs(c)}}) }dfs(0)结果:0,1,2,3,4
这里只是恰巧是顺数,如果把graph[0]改为[4,1]那结果会变成0,4,3,1,2
广度优先
const visited = new Set()
const dfs = (n) => {visited.add(n)const q = [n]while(q.length){const n = q.shift()console.log(n)graph[n].forEach(c => {if(!visited.has(c)){q.push(c) visited.add(c)}})} }dfs(0)结果
0,1, 4,2,3
备注
上面的set是用来做去重的
使用场景
社交网络。
社交网络是典型的网络结构,图可以用点来表达社交关系中的人,用点与点之间的连接来表达人与人的关系。比如我们想要去表示谁认识谁、谁和谁沟通、谁能够影响谁等人与人之间的关系。一个具体的例子是在小红书上,比如,A 关注了 B 的小红书,可以用 A 指向 B 的线来连接表示。这些人与人的社交信息,可以用来去解释社交网络的信息流动。人与人之间的联系也定义了我们是谁。
交通网络。
交通网络也可以用图来表达。比如所有的城市可以用图的节点来表示,城市间的交通渠道可以用边来表示。像最近大家关注的疫情封城措施,也可以用数据结构来理解,就是把交通网络图的一些边进行了阻隔。
互联网网站连接。
我们经常看到网站上会有指向其他网址的超链接。如果我们把互联网所有的网页定义成图的节点,那么网页与网页之间的边就是这些链接了。如果大家熟悉 Google 经典的网页排名算法 PageRank,就会知道,搜索引擎正是用指向一个网页的引用数量去判断一个网页的质量。
第 13 讲:用图来表达更为复杂的数据关系 · 数据结构精讲:从原理到实战 · 看云
更多
https://www.cnblogs.com/jaxu/p/11338294.html
相关文章:

图-基础概念
是什么 图是一种抽象的数据类型,在图中的数据元素通常称作节点,V是所以定点的集合,E是所有边的集合 图的分类 有向图 如果两个订单v,w,只能由v向w,而不能w向v,那么我们就把何种情况叫做一个从…...

Javascript前端基础面试(十)
MVVM Vue MVVM这一篇就够啦!_vue r mvvm-CSDN博客 点容器内的图标,图标边框变成border 1px solid red,点空白处重置 <div id"container"> <img src"icon.png" alt"Icon" class"icon"> <!…...
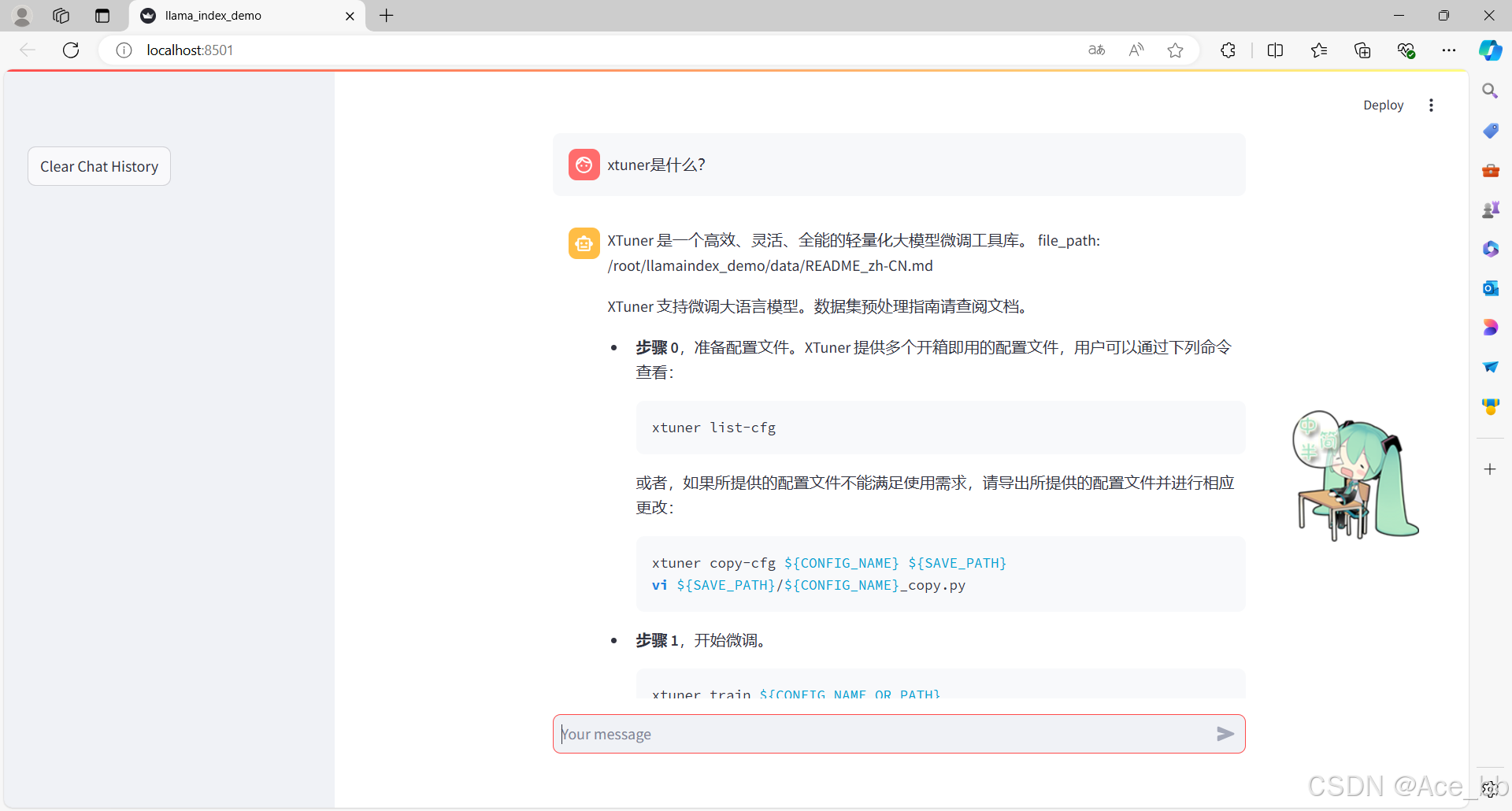
书生大模型实战营闯关记录----第五关:LlamaIndex+Internlm2 RAG实践Demo:效果对比,文档加载,向量库构建,检索器,模型推理
文章目录 1. 前置知识RAG背景RAG 效果比对 2. 环境、模型准备2.1 配置基础环境2.2 安装 Python环境和依赖包2.3 下载 Sentence Transformer 模型2.4 下载 NLTK 相关资源 3. LlamaIndex HuggingFaceLLM4. LlamaIndex RAG加载文档构建向量存储索引库检索器RAG代码 5. LlamaIndex …...
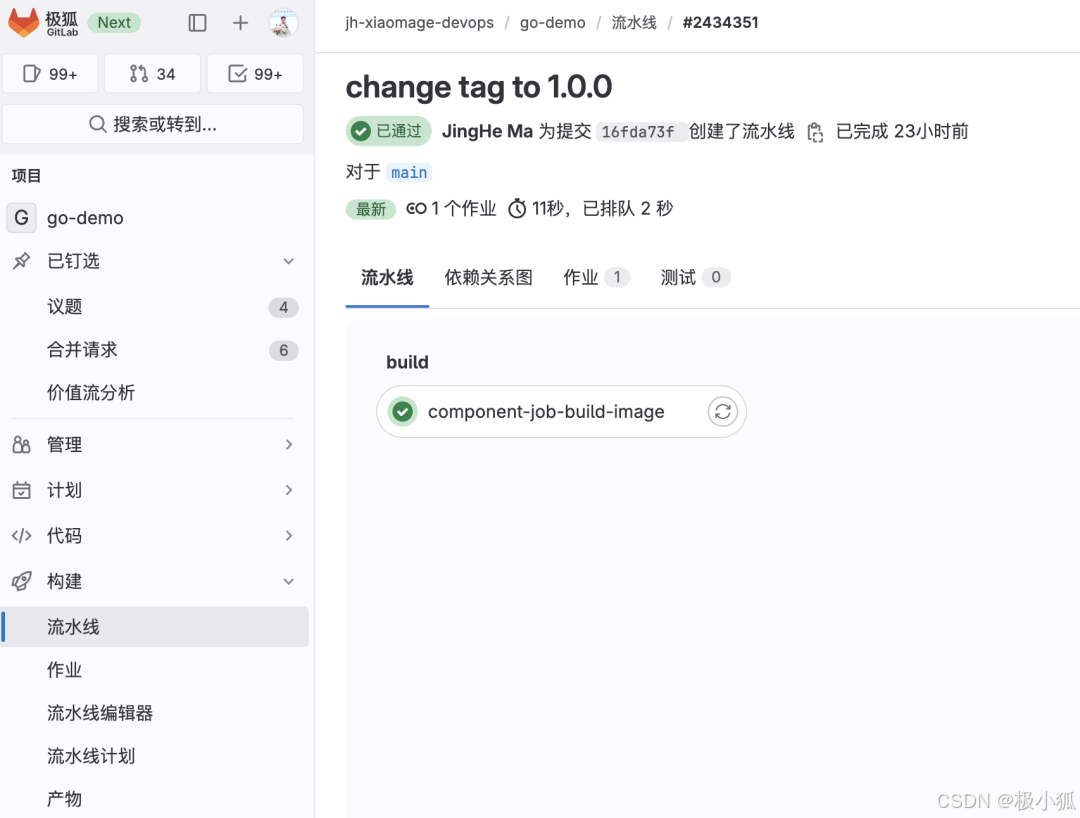
如何使用极狐GitLab CI/CD Component Catalog?【上】
极狐GitLab 是 GitLab 在中国的发行版,专门面向中国程序员和企业提供企业级一体化 DevOps 平台,用来帮助用户实现需求管理、源代码托管、CI/CD、安全合规,而且所有的操作都是在一个平台上进行,省事省心省钱。可以一键安装极狐GitL…...
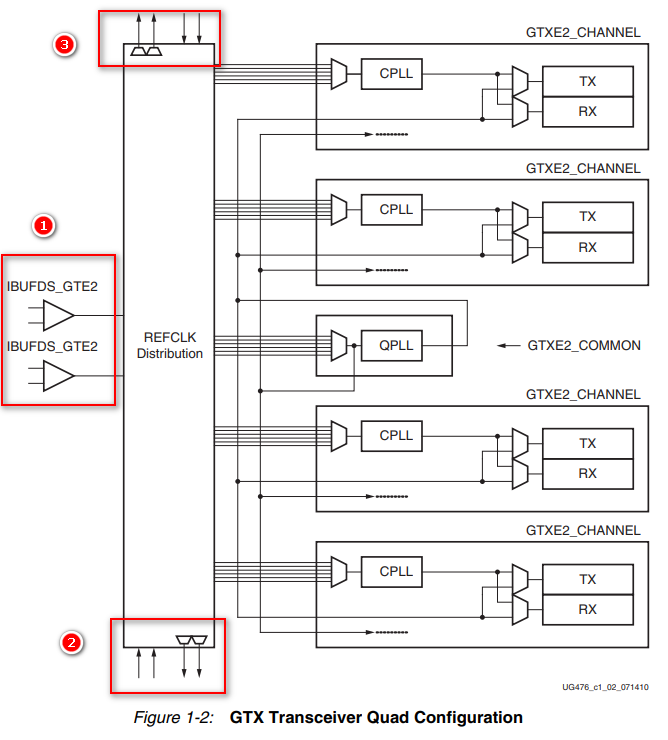
详解Xilinx FPGA高速串行收发器GTX/GTP(3)--GTX的时钟架构
目录 1、参考时钟 2、时钟方案 2.1、单个外部参考时钟驱动单个QUAD中的多个transceiver 2.2、单个外部参考时钟驱动多个QUAD中的多个transceiver 2.3、同一个Quad中,多个GTX Transceiver使用多个参考时钟 2.4、不同Quad中,多个GTX Transceiver 使用多个参考时钟 3、QP…...
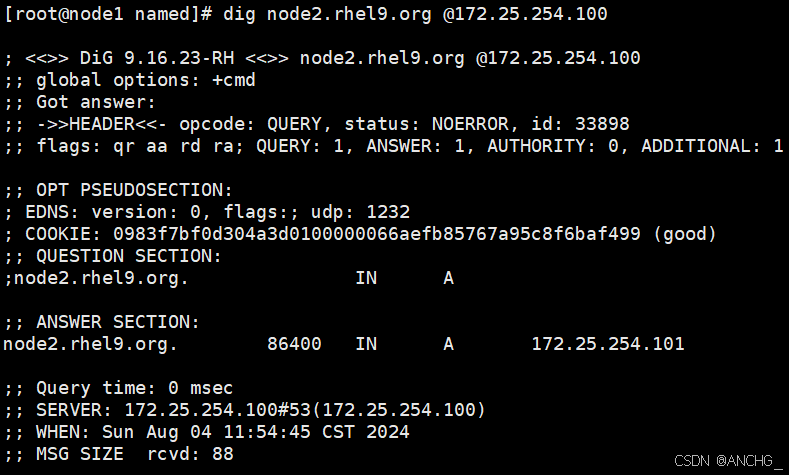
简单搭建dns服务器
目录 一.安装服务 二.编写子配置文件 三.编写主配置文件 四.编写文件 五.重启服务测试 配置端:IP地址为172.25.254.100、主机名为node1.rhel9.org 测试端:IP地址为172.25.254.101、主机名为node2.rhel9.org 一.安装服务 [rootnode1 ~]# dnf inst…...
)
大数据进阶(Advanced Big Data)
大数据进阶(Advanced Big Data) 目录 引言大数据架构 Lambda架构Kappa架构 大数据技术栈 数据采集与预处理数据存储与管理数据处理与分析数据可视化与展示 大数据分析方法 机器学习深度学习自然语言处理图数据分析 大数据在工业中的应用 制造业能源管理…...

微信小程序开发优惠券制作源码
微信小程序开发优惠券制作源码。制作一个自带流量的小程序商城,功能强大玩法新,轻松实现引流,推广,卖货,分销,会员管理,直播等多种功能需求需要哪些编辑代码源码呢?http://m.bokequ.com/list/124-2.html 代码分享 <!DOCTYPE HTML> <html xmlns"http://www.w3.o…...

mongodb的安装操作记录
mongodb的安装操作记录 1 上传软件包,并解压 [rootmonitor local]# tar -xvf mongodb-linux-x86_64-rhel70-7.0.12.tgz mongodb-linux-x86_64-rhel70-7.0.12/LICENSE-Community.txt mongodb-linux-x86_64-rhel70-7.0.12/MPL-2 mongodb-linux-x86_64-rhel70-7.0.1…...

C++客户端Qt开发——多线程编程(二)
多线程编程(二) ③线程池 Qt中线程池的使用 | 爱编程的大丙 1>线程池 我们使用线程的时候就去创建一个线程,这样实现起来非常简便,但是就会有一个问题:如果并发的线程数量很多,并且每个线程都是执行…...

ubuntu20复现NBV探索
官网代码 后退地平线下一个最佳景观规划师 这个代码有些久远,issue里面有人已经在ubuntu20里面使用了3dmr,但是他那个代码我也运行不成功,docker网络一直也不佳,所以还是自己重新修改源码靠谱。 最终实现的代码等有时间上传到gi…...
【51单片机仿真】基于51单片机设计的温湿度采集检测系统仿真源码文档视频——文末资料下载
演示 目录 1.系统功能 2.背景介绍 3.硬件电路设计 4.软件设计 4.1 主程序设计 4.2 温湿度采集模块程序设计 4.3 LCD显示屏程序设计 5.系统测试 6.结束语 源码、仿真、文档视频等资料下载链接 1.系统功能 该系统通过与AT89C51单片机、LCD1602显示屏和DHT11温湿度传感器…...

【Hadoop-驯化】一文学会hadoop访问hdfs中常用命令使用技巧
【Hadoop-驯化】一文学会hadoop访问hdfs中常用命令使用技巧 本次修炼方法请往下查看 🌈 欢迎莅临我的个人主页 👈这里是我工作、学习、实践 IT领域、真诚分享 踩坑集合,智慧小天地! 🎇 免费获取相关内容文档关注&am…...

【Spring】Bean详细解析
1.Spring Bean的生命周期 整体上可以简单分为四步:实例化 —> 属性赋值 —> 初始化 —> 销毁。初始化这一步涉及到的步骤比较多,包含 Aware 接口的依赖注入、BeanPostProcessor 在初始化前后的处理以及 InitializingBean 和 init-method 的初始…...

决策树总结
决策树总结 决策树是一种广泛应用的机器学习算法,它模拟了人类进行决策时的逻辑思维过程,通过构建一棵树状结构来进行数据的分类或回归预测。决策树模型因其直观易懂、易于解释、能够处理多类问题以及无需进行复杂的特征缩放等优点,在数据挖…...

通俗易懂!495页看漫画学Python入门教程(全彩版)Git首发破万Star
前言 在编程的世界里,Python无疑是一颗璀璨的明星。从最初作为打发圣诞节闲暇时间的项目,到如今成为最受欢迎的程序设计语言之一,Python以其简洁、易学、强大的特点吸引了无数编程爱好者。然而,对于初学者来说,编程的…...

websocket实现简易聊天室
websocket实现简易聊天室 又做了一个关于websocket广播和在线人数统计的练习,实现一个简易的聊天室。 前端vue3 前端里的内容主要包含: 1.css的animation来实现公告从右到左的轮播。 2.websocket的onmessage里对不同消息的处理。 <template>&l…...
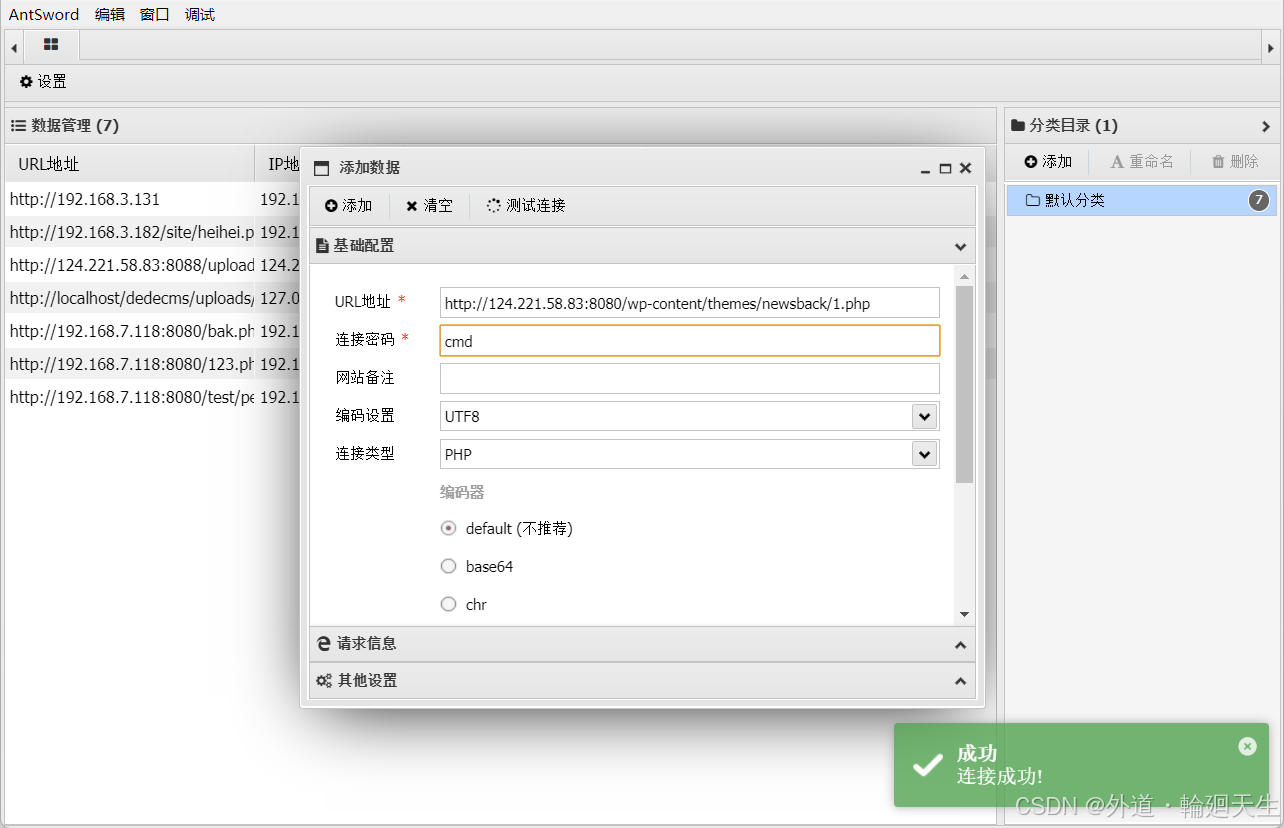
vulhub-wordpress
1.打开wordpress关卡,选择简体中文 添加信息——点击安装WordPress 安装完成——登录 点击外观——编辑主题 可以加入一句话木马,但是我写入的是探针文件 也可以去上传一个带有木马的主题 上传之后会自动解压 1.php就是里面的木马文件...

【机器学习算法基础】(基础机器学习课程)-10-逻辑回归-笔记
一、模型的保存与加载 逻辑回归是一种常见的机器学习算法,广泛用于分类问题。为了在不同的时间或环境下使用训练好的模型,我们通常需要将其保存和加载。 保存模型 训练模型:首先,你需要用你的数据训练一个逻辑回归模型。例如&…...

自动驾驶行业知识汇总
应届生月薪2W的自动驾驶开发、机器人、后端开发,软件开发该如何学习相关技术栈_哔哩哔哩_bilibili 两万字详解自动驾驶开发工具链的现状与趋势 (qq.com) 九章智驾 - 2023年度文章大合集 (qq.com) 九章 - 2022年度文章大合集 (qq.com)...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
