灵茶八题 - 子序列 +w+
灵茶八题 - 子序列 +w+
题目描述
给你一个长为 n n n 的数组 a a a,输出它的所有非空子序列的元素和的元素和。
例如 a = [ 1 , 2 , 3 ] a=[1,2,3] a=[1,2,3] 有七个非空子序列 [ 1 ] , [ 2 ] , [ 3 ] , [ 1 , 2 ] , [ 1 , 3 ] , [ 2 , 3 ] , [ 1 , 2 , 3 ] [1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] [1],[2],[3],[1,2],[1,3],[2,3],[1,2,3],元素和分别为 1 , 2 , 3 , 3 , 4 , 5 , 6 1,2,3,3,4,5,6 1,2,3,3,4,5,6,所以答案为 1 + 2 + 3 + 3 + 4 + 5 + 6 = 24 1+2+3+3+4+5+6=24 1+2+3+3+4+5+6=24。
由于答案很大,你需要输出答案模 1 0 9 + 7 10^9+7 109+7 后的结果。
输入格式
第一行输入一个整数 n ( 1 ≤ n ≤ 2 ⋅ 1 0 5 ) n\ (1\le n \le 2\cdot 10^5) n (1≤n≤2⋅105)。
第二行输入 n n n 个整数,表示数组 a a a 中的元素 ( 0 ≤ a [ i ] ≤ 1 0 9 ) (0\le a[i] \le 10^9) (0≤a[i]≤109)。
输出格式
一个整数,表示 a a a 的所有非空子序列的元素和的元素和,模 1 0 9 + 7 10^9+7 109+7 后的结果。
样例 #1
样例输入 #1
3
1 2 3
样例输出 #1
24
提示
对于子序列, 每一个出现的次数为2的n - 1次方
#include<bits/stdc++.h>using namespace std;typedef long long ll;
typedef pair<int, int>PII;
const int N=2e5+10;
const int MOD = 1e9 + 7;
const int INF=0X3F3F3F3F;
const int dx[]={-1,1,0,0,-1,-1,+1,+1};
const int dy[]={0,0,-1,1,-1,+1,-1,+1};
const int M = 1e7 + 10;int t;int main()
{int n;cin >> n;ll res = 0;//对于子序列,每个元素出现的次数为2的n - 1次方for(int i = 1; i <= n; i ++){int x;cin >> x;res += x;}for(int i = 1; i <= n - 1; i ++){res = res * 2 % MOD;}cout << res << endl;return 0;
}
相关文章:

灵茶八题 - 子序列 +w+
灵茶八题 - 子序列 w 题目描述 给你一个长为 n n n 的数组 a a a,输出它的所有非空子序列的元素和的元素和。 例如 a [ 1 , 2 , 3 ] a[1,2,3] a[1,2,3] 有七个非空子序列 [ 1 ] , [ 2 ] , [ 3 ] , [ 1 , 2 ] , [ 1 , 3 ] , [ 2 , 3 ] , [ 1 , 2 , 3 ] [1],[…...

为什么美元债务会越来越多?
美元债务规模持续膨胀,其背后原因复杂多样,可归结为以下几个主要因素: 财政赤字和刺激政策是导致美元债务增加的重要原因。美国政府长期面临财政赤字问题,支出远超收入,为弥补这一缺口,政府不得不大量发行…...

二维凸包算法 Julia实现
问题描述:给定平面上 n n n 个点的集合 Q Q Q,求其子集 P P P 构成 Q Q Q 的凸包,即 ∀ p ∈ Q , ∃ p 0 , p 1 , p 2 ∈ P \forall p \in Q, \exist p_0, p_1, p_2 \in P ∀p∈Q,∃p0,p1,p2∈P 使得点 p p p 在以点 p 0 , p 1 …...
python dash框架
Dash 是一个用于创建数据分析型 web 应用的 Python 框架。它由 Plotly 团队开发,并且可以用来构建交互式的 web 应用程序,这些应用能够包含图表、表格、地图等多种数据可视化组件。 Dash 的特点: 易于使用:Dash 使用 Python 语法…...

2.外部中断(EXTI)
理论 NVIC:嵌套向量中断控制器(解释教程) 外部通用中断线(EXTI0~EXTI15):每个GPIO设置成中断模式,与中断控制器连接的线 外部中断触发方式 上升沿触发、下降沿触发、双边沿触发 外部中断触发函数 在stm32f1xx_it.c文件…...

Python | SyntaxError: invalid syntax 深度解析
Python | SyntaxError: invalid syntax 深度解析 在Python编程中,SyntaxError: invalid syntax是一个常见的错误,它表明Python解释器在尝试解析代码时遇到了语法问题。这个错误通常是由于代码中存在拼写错误、缺少符号(如括号、冒号或逗号&a…...
付费进群系统源码原版最新修复全开源版
付费进群,和平时所见到的别人拉你进群是不一样的,付费进群需要先缴费以后,才会看到群的二维码,扫码进群或者是长按二维码图片识别进群,付费进群这个功能广泛应用于拼多多的砍价群,活动的助力群,…...

Docker容器部署的SpringBoot项目jar包,上传文件但是找不到路径的问题
在docker容器内部署的jar包运行后,请求访问都没有问题,在文件上传时,发现上传图片接口响应成功,但是图片路径报404错误,发现找不到路径。 在服务器上查看也没有找到相关图片。 原因: 启动docker镜像时没…...
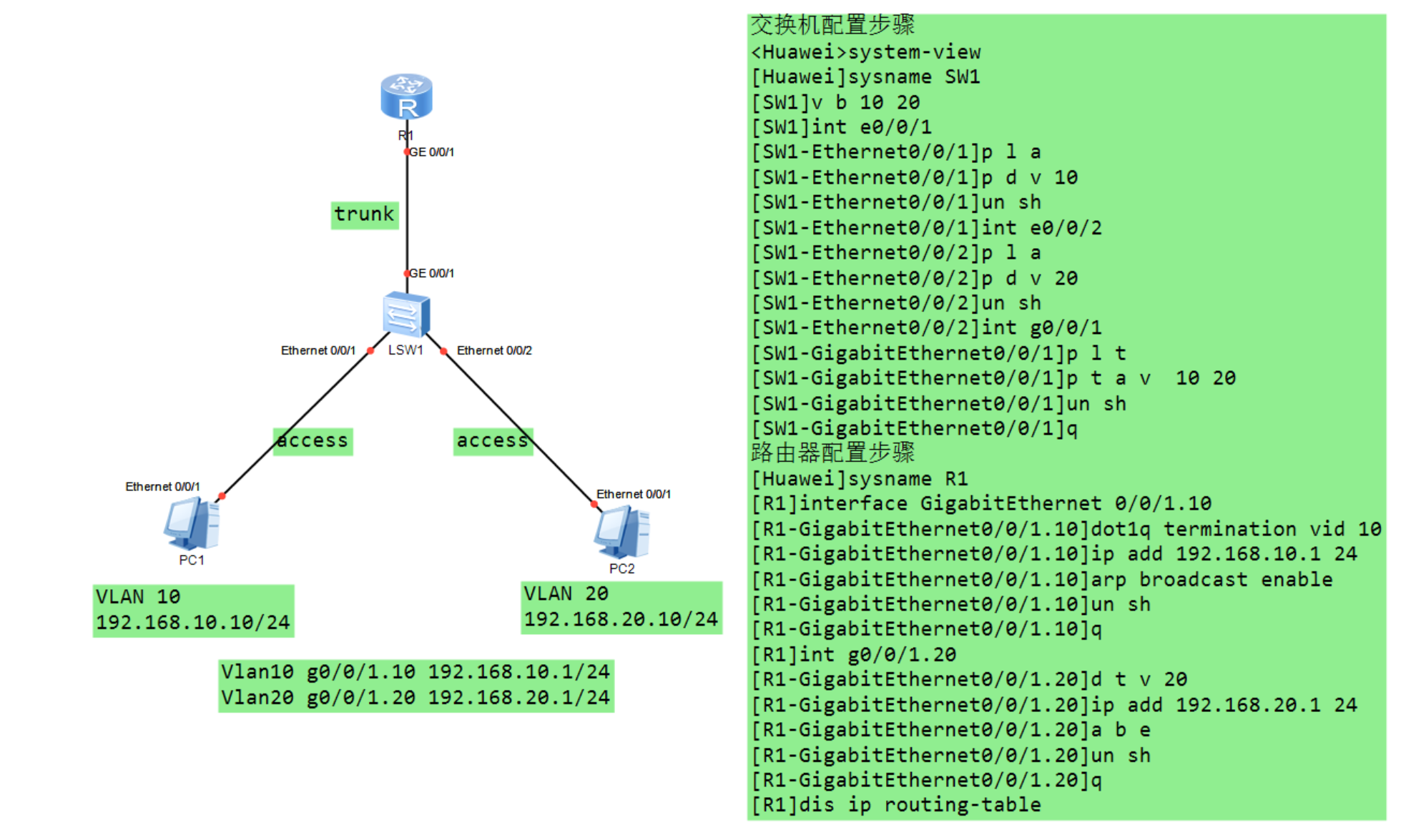
云计算学习——5G网络技术
系列文章目录 提示:仅用于个人学习,进行查漏补缺使用。 Day1 网络参考模型 Day2 网络综合布线与应用 Day3 IP地址 Day4 华为eNSP网络设备模拟器的基础安装及简单使用 Day5 交换机的基本原理与配置 Day6 路由器的原理与配置 Day7 网络层协议介绍一 Day8 传…...

matlab仿真 信道编码和交织(上)
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第八章内容,有兴趣的读者请阅读原书) clear all N10;%信息比特的行数 n7;%hamming码组长度n2^m-1 m3;%监督位长度 [H,G]hammgen(m);%产生(n,n-…...

基于YOLOv8的高压输电线路异物检测系统
基于YOLOv8的高压输电线路异物检测系统 (价格88) 包含 【“鸟窝”,“风筝”,“气球”,“垃圾”】 4个类 通过PYQT构建UI界面,包含图片检测,视频检测,摄像头实时检测。 (该系统可以根据数…...

23款奔驰GLS450加装原厂电吸门配置,提升车辆舒适性和便利性
今天是一台22款奔驰GLS450,车主是佛山的 以前被不良商家坑了 装了副厂的电吸门 刚开始就很正常 用了半年之后 就开始开不了门,被锁在里面,刚开始车主以为是零件坏了 后来越来越频繁,本来是为了家里老人小孩关门方便而升级的&#…...

git操作流程笔记
1、在本地项目文件夹右击鼠标点击Git Bash Here 2、输入git init,这个目录变成git可以管理的仓库,会出现一个.git文件夹,如果没出现的话需要选择“显示隐藏文件”(不会的同学自行百度一下) 3、绑定本地仓库与远程仓库…...

【QT】常用控件-上
欢迎来到Cefler的博客😁 🕌博客主页:折纸花满衣 目录 👉🏻QWidgetenabledgeometryrect制作上下左右按钮 window frame 的影响window titlewindowIcon代码示例: 通过 qrc 管理图片作为图标 windowOpacitycursor使用qrc自…...
帮助网站提升用户参与度的5个WordPress插件
仅靠编写精彩的内容、设计精美的图像和创建简化的客户旅程不足以提高网站参与度。您需要让用户在首次访问后继续与您的网站互动并成为回访者,才能真正吸引您所追求的兴趣。 幸运的是,对于 WordPress 用户来说,有数百种工具可用于提高用户参与…...

理解 Python 中的 @wraps:保留函数元数据
一.介绍 在本文中,我们将了解 wraps。在 Python 中使用装饰器时,您可能会遇到原始函数的元数据丢失的情况。这时,functools 模块中的 wraps 装饰器就可以派上用场了。让我们深入了解 wraps 的作用及其重要性。 二.简单装饰器的问题 首先&a…...
cjson
文章目录 概述编译cjson_test 小结 概述 在网络传输中,网络数据序列化,常用的有那么几种,json,protobuf都是很常用的,这一篇来写下json。 Json常用的有几个,rapidjson,jsoncpp,还有…...

Docker data root 目录更改
有时候受限于系统根目录空间的限制,需要将 docker data root 目录更改为其它目录,如单独挂载一个磁盘或存储。本篇文章介绍如何操作。 修改docker 工作目录 修改配置文件/etc/docker/daemon.json(在19.x 版本之前使用grapth) {&q…...
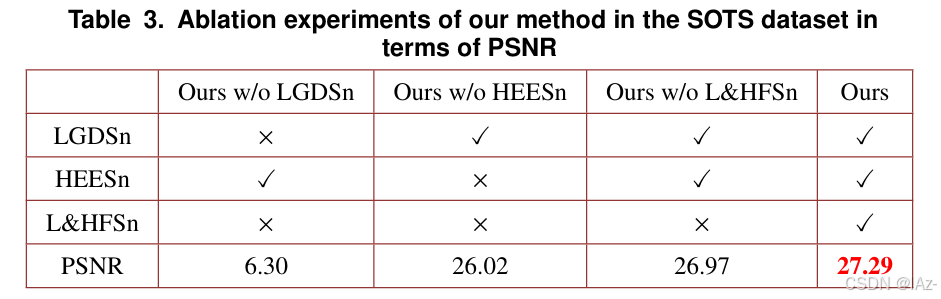
[CR]厚云填补_SEGDNet
Structure-transferring edge-enhanced grid dehazing network Abstract 在过去的二十年里,图像去雾问题在计算机视觉界受到了极大的关注。在雾霾条件下,由于空气中水汽和粉尘颗粒的散射,图像的清晰度严重降低,使得许多计算机视觉…...
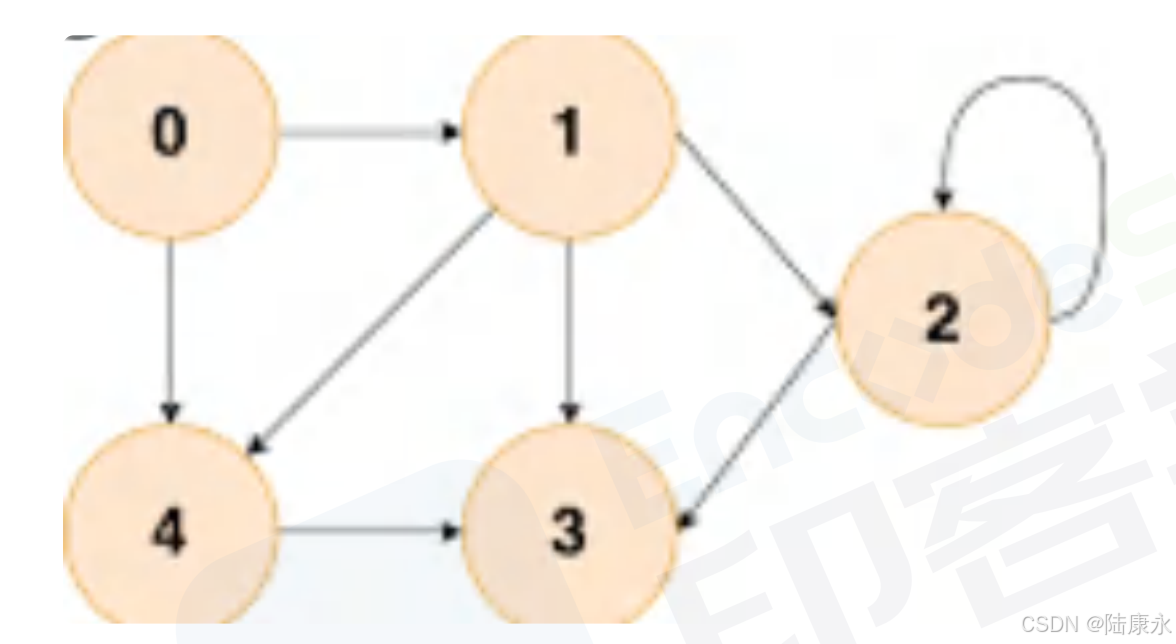
图-基础概念
是什么 图是一种抽象的数据类型,在图中的数据元素通常称作节点,V是所以定点的集合,E是所有边的集合 图的分类 有向图 如果两个订单v,w,只能由v向w,而不能w向v,那么我们就把何种情况叫做一个从…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
