【Python机器学习】支持向量机——手写数字识别问题
基于SVM的数字识别步骤:
1、收集数据:提供的文本文件
2、准备数据:基于二值图像构造向量
3、分析数据:对图像向量进行目测
4、训练算法:采用两种不同的核函数,并对径向基核函数采用不同的设置来运行SMO算法
5、测试算法:编写一个函数来测试不同的核函数并计算错误率
6、使用算法:一个图像识别的完整应用还需要一些图像处理的知识。
构建一个系统去测试手写数字上的分类器:
def img2vector(filename):returnVect=zeros((1,1024))fr=open(filename)for i in range(32):lineStr=fr.readline()for j in range(32):returnVect[0,32*i+j]=int(lineStr[j])return returnVectdef loadImages(dirName):from os import listdirhwLabels=[]trainingFileList=listdir(dirName)m=len(trainingFileList)trainingMat=zeros((m,1024))for i in range(m):fileNameStr=trainingFileList[i]fileStr=fileNameStr.split('.')[0]classNumStr=int(fileStr.split('_')[0])if classNumStr==9:hwLabels.append(-1)else:hwLabels.append(1)trainingMat[i,:]=img2vector('%s/%s'%(dirName,fileNameStr))return trainingMat,hwLabelsdef testDigits(kTup=('rbf',10)):dataArr,labelArr=loadImages('trainingDigits')b,alphas=svm_11.smoP(dataArr,labelArr,200,0.0001,10000,kTup)dataMat=mat(dataArr)labelMat=mat(labelArr).transpose()svInd=nonzero(alphas.A>0)[0]sVs=dataMat[svInd]labelSV=labelMat[svInd]print('there are %d Support Vectors' % shape(sVs)[0])m,n=shape(dataMat)errorCount=0for i in range(m):kernelEval=svm_11.kernelTrans(sVs,dataMat[i,:],kTup)predict=kernelEval.T*multiply(labelSV,alphas[svInd])+bif sign(predict)!=sign(labelArr[i]):errorCount=errorCount+1print('训练集错误率:',(float(errorCount)/m))dataArr,labelArr=loadImages()errorCount = 0dataMat=mat(dataArr)labelMat=mat(labelArr).transpose('testDigits')m,n=shape(dataMat)for i in range(m):kernelEval = svm_11.kernelTrans(sVs, dataMat[i, :], kTup)predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + bif sign(predict) != sign(labelArr[i]):errorCount = errorCount + 1print('测试集错误率:', (float(errorCount) / m))testDigits()函数loadImages()是作为k近邻算法中的一部分出现的。它已经被重构为自身的一个函数。其中最大的区别在于,支持向量机中类别标签为-1和+1,,因此,一旦碰到数字9,则输出类别标签-1,否则输出+1,。本质上,支持向量机是一个二类分类器,其分类结果不是+1就是-1。
testDigits()和testRbf()几乎一样,区别在于它调用了loadImages()函数来获得类别标签和数据。kTup是输入参数。
上述代码运行结果:

相关文章:

【Python机器学习】支持向量机——手写数字识别问题
基于SVM的数字识别步骤: 1、收集数据:提供的文本文件 2、准备数据:基于二值图像构造向量 3、分析数据:对图像向量进行目测 4、训练算法:采用两种不同的核函数,并对径向基核函数采用不同的设置来运行SMO算法…...

学习笔记-Cookie、Session、JWT
目录 一、验证码的生成与校验 1. 创建生成验证码的工具类 2. 写一个 Controller 3. 实现验证码验证 1. 获取验证码 2. 验证码请求过程 3. 验证码的校验 4. 原理说明 5. 验证 6. 总结 二、JWT登录鉴权 1. 为什么要做登录鉴权? 2. 什么是 JWT 3. JWT相比…...

题海战术,面试必胜秘诀
目录 1.Java 的优势是什么?2.什么是 Java 的多态特性?3.Java 中的参数传递是按值还是按引用?4.为什么 Java 不支持多重继承?5.什么是 Java 中的不可变类?总结 题目 来自面试鸭刷题神器 1.Java 的优势是什么? Java 的跨平台性、垃圾回收机制以及其强…...
——命令模式)
设计模式详解(十九)——命令模式
命令模式简介 命令模式定义 命令模式(Command Pattern)是一种在面向对象程序设计中常用的行为型设计模式。命令模式的核心思想在于将请求封装成一个对象,从而使发出请求的责任和执行请求的责任分割开。它可以让请求发送者和请求接收者之间消…...

实战:MySQL数据同步神器之Canal
1.概叙 场景一:数据增量实时同步 项目中业务数据量比较大,每类业务表都达到千万级别,虽然做了分库分表,每张表数据控制在300W以下,但是效率还是达不到要求,为了提高查询效率,打算使用ES进行数…...

5.6软件工程-运维
运维 系统转换系统维护系统评价练习题 系统转换 新老系统的转换 系统转换是指:新系统开发完毕,投入运行,取代现有系统的过程,需要考虑多方面的问题,以实现与老系统的交接,有一下三种转换计划: …...

在JavaScript中如何确保构造函数只被new调用
构造函数是一个特殊的函数,用于初始化一个新创建的对象。它是在创建对象时自动调用的。构造函数通常用于为对象的属性赋值,或者执行其他必要的设置。 使用函数名大写字母开头,这是一种命名约定,用于区分构造函数和普通函数。如何…...

【数据结构算法经典题目刨析(c语言)】反转链表(图文详解)
💓 博客主页:C-SDN花园GGbond ⏩ 文章专栏:数据结构经典题目刨析(c语言) 目录 一、题目描述 二、思路分析 三、代码实现 一、题目描述: 二、思路分析 : 通过三个指针n1,n2,n3来实现链表的反转 1.首先初始化 n1为…...

机器学习之争:Python vs R,谁更胜一筹?
一、引言 随着人工智能和大数据的迅速发展,机器学习已成为现代科技的重要组成部分。在医疗、金融、零售、制造等多个领域,机器学习技术的应用无处不在。从数据分析到预测建模,再到深度学习,机器学习正在改变我们的工作和生活方式…...

Vulnhub靶机:JANGOW_ 1.0.1
目录 前言: 一、安装虚拟机Jangow:1.0.1靶机 二、Web部分 前言: 难度:简单,本文使用VirtualBox打开,下载地址: https://download.vulnhub.com/jangow/jangow-01-1.0.1.ova 一、安装虚拟机J…...

Python脚本实现USB自动复制文件
USB驱动器作为常见的数据存储设备,经常用于数据传输和备份。 然而,我们在手动处理文件复制可能效率低下且容易出错。 因此,我们可以利用Python编写脚本来自动化这一过程,提高效率和数据安全性。 准备工作 首先,我们需…...

【C++学习第19天】最小生成树(对应无向图)
一、最小生成树 二、代码 1、Prim算法 #include <cstring> #include <iostream> #include <algorithm>using namespace std;const int N 510, INF 0x3f3f3f3f;int n, m; int g[N][N]; int dist[N]; bool st[N];int prim() {memset(dist, 0x3f, sizeof di…...

第一个 Flask 项目
第一个 Flask 项目 安装环境创建项目启动程序访问项目参数说明Flask对象的初始化参数app.run()参数 应用程序配置参数使用 Flask 的 config.from_object() 方法使用 Flask 的 config.from_pyfile() 方法使用 Flask 的 config.from_envvar() 方法步骤 1: 设置环境变量步骤 2: 编…...
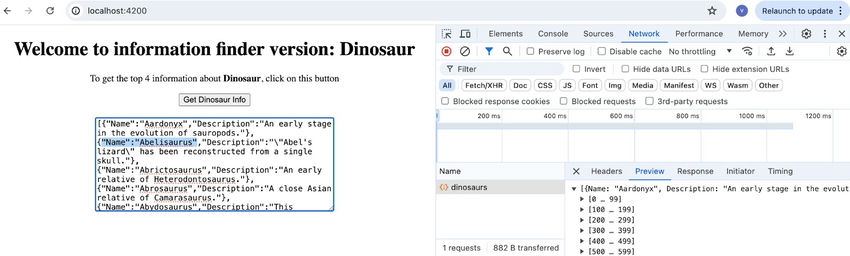
利用 Angular 发挥环境的力量
一.介绍 您是否曾想过如何在不同的环境中为同一应用设置不同的颜色、标题或 API 调用?可以肯定的是,生产 API 和测试 API 是不同的,应谨慎使用。部署时,我们不会在项目的所有地方手动更改所有 API 调用。不应这样做,因…...

Vue3+TypeScript+printjs 实现标签批量打印功能
前言:临时性需求没怎么接触过前端,代码实现有问题及优化点希望大佬可以留言告知一下 开发工具:VS CODE 界面开发:Vue3TypeScriptElementPlus 打印组件:Print-JS 前端打印入口图: 标签页面: …...

微信文件如何直接打印及打印功能在哪里设置?
在数字化时代,打印需求依旧不可或缺,但传统打印店的高昂价格和不便操作常常让人头疼。幸运的是,琢贝打印作为一款集便捷、经济、高效于一体的网上打印平台,正逐渐成为众多用户的首选。特别是通过微信小程序下单,更是让…...

dataX -20240804-master分支
1、相关报错 Error: java.io.IOException: java.lang.RuntimeException: ORC split generation failed with exception: org.apache.orc.impl.SchemaEvolution$IllegalEvolutionException: ORC does not support type conversion from file type struct<nanos:int> (10)…...

【网络】传输层
传输层 一、预备知识1、端口号1、端口号范围划分2、知名端口号3、两个问题4、netstat && iostate5、pidof6、谈下面协议始终铭记两个问题 二、UDP协议(简单)1、UDP协议端格式2、UDP的特点3、面向数据报4、UDP缓冲区 三、TCP协议(重点…...

学生管理系统之更新和删除、筛选
学生管理系统之更新和删除 建立新的窗口 添加组件 进行布局 使用Widget把二个放在一块,作为一列,然后全选进行栅格布局,最后添加弹簧进行微调。 编写增加的槽函数 在主函数中调用对话框...

教您一键批量下载拼多多批发图片信息,节省时间
图片是电商的核心展示手段,高质量、吸引人的图片能显著提升商品吸引力,增强用户体验,促进购买决策。良好的视觉呈现有助于品牌形象的塑造,提高转化率和客户满意度,对电商平台的流量和销售业绩具有直接影响。 使用图快…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
