nginx: [error] open() “/run/nginx.pid“ failed (2: No such file or directory)
今天 准备访问下Nginx服务，但是 启动时出现如下报错：（80端口被占用，没有找到nginx.pid文件）
解决思路：
1、 查看下排查下nginx服务
#确认下nginx状态
ps -ef|grep nginx
systemctl status nginx#查看端口占用情况
netstat -apn|grep 80从ps命令看nginx服务是启动状态，而systemctl看却是失败，80端口也是nginx占用，自相矛盾。
2、查看nginx.pid文件情况
查看目录/run/下没有nginx.pid文件，原因找到
解决办法：
nginx.pid文件，在刚安装的时候就是没有,其实在启动 nginx 时自动生成，里面存放的是 当前 nginx 住进程的PID ，nginx相关操作都与要调用这个文件。
1、看网上的解决办法，新建一个nginx.pid文件（不管用）
2、杀掉nginx进程，重新启动
killall nginx
#或者找到nginx的pid 杀掉进程相关文章：
nginx: [error] open() “/run/nginx.pid“ failed (2: No such file or directory)
今天 准备访问下Nginx服务，但是 启动时出现如下报错：（80端口被占用，没有找到nginx.pid文件） 解决思路： 1、 查看下排查下nginx服务 #确认下nginx状态 ps -ef|grep nginx systemctl status nginx#查看端口…...
＜数据集＞BDD100K人车识别数据集＜目标检测＞
数据集格式：VOCYOLO格式 图片数量：15807张 标注数量(xml文件个数)：15807 标注数量(txt文件个数)：15807 标注类别数：7 标注类别名称： [pedestrian, car, bus, rider, motorcycle, truck, bicycle] 序号…...
利用SSE打造极简web聊天室
在B/S场景中，通常我们前端主动访问后端可以使用axios，效果很理想，而后端要访问前端则不能这样操作了，可以考虑SSE、websocket等方式，实时和性能均有保障。 下面给出一个简单的SSE例子，后端是nodeexpress&am…...
代码随想录第二十天|动态规划（4）
目录 LeetCode 322. 零钱兑换 LeetCode 279. 完全平方数 LeetCode 139. 单词拆分 总结 LeetCode 322. 零钱兑换 题目链接：LeetCode 322. 零钱兑换 思想：首先定义dp数组的含义，dp[j]即总金额为j的情况下所需的最少的硬币个数。接下来确定…...
TreeSize：免费的磁盘清理与管理神器，解决C盘爆满的燃眉之急
目录 TreeSize：免费的磁盘清理与管理神器，解决C盘爆满的燃眉之急 一、TreeSize介绍 二、下载安装TreeSize 2.1、下载地址 2.2、下载步骤 2.3、安装步骤 三、professional版的TreeSize试用 3.1、分析磁盘空间 3.2、显示拓展名统计信息 3.3、显…...
如何建立自己的技术知识体系
已经工作五年了，慢慢的觉得不能再继续像以前一样，工作中用到啥才去学啥，平时积累的知识也是非常的零碎，我现在要做的就是建立自己的技术知识体系。 我感觉学习技术知识就想是探索一个城市一样，技术知识体系就好比是这…...
JS优化了4个自定义倒计时
<!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><title>4个自定义倒计时</title><style>* {margin: 0;padding: 0;box-sizing: border-box;user-select: none;body {background: #0b1b2c;}}hea…...
模型实战（25）之 基于LoFTR深度学习匹配算法实现图像拼接
模型实战（25）之 基于LoFTR深度学习匹配算法实现图像拼接 图像拼接在全景图、大图或者多目场景下经常会被使用，常用的方法有传统图像处理算法和深度学习直接获取对应点的算法传统图像处理算法过程繁琐，阈值少且整体算法结果对调参比较敏感，其主要通过形状、特征点等描述子对…...
计算机毕业设计Python+Spark知识图谱高考志愿推荐系统 高考数据分析 高考可视化 高考大数据 大数据毕业设计
《Spark高考推荐系统》开题报告 一、选题背景及意义 1. 选题背景 随着我国高考制度的不断完善和大数据技术的飞速发展，高考志愿填报已成为考生和家长高度关注的重要环节。传统的志愿填报方式依赖于考生和家长手动查找和对比各种信息，不仅效率低下且容…...
【python】文件
在python中可以通过文件操作，将数据保存到计算机硬盘中文件，可以包含文本数据，也可以包含二进制数据(图片，视频，音频等)。 目录 前言 正文 一、基本语法 1、函数open()打开file 返回一个文件对象 1.1、文件路径 1&a…...
《Attention Is All You Need》核心观点及概念
这个文件据说是一篇很厉害的AI论文，https://arxiv.org/pdf/1706.03762 这篇论文《Attention Is All You Need》确实是AI领域中的一个里程碑，它改变了我们处理语言的方式。 下面小编会用简单的语言来解释这篇文章的核心观点和学术概念，并告诉大家它为什么很厉害。 核心观点…...
【中项】系统集成项目管理工程师-第9章 项目管理概论-9.9价值交付系统
前言：系统集成项目管理工程师专业，现分享一些教材知识点。觉得文章还不错的喜欢点赞收藏的同时帮忙点点关注。 软考同样是国家人社部和工信部组织的国家级考试，全称为“全国计算机与软件专业技术资格（水平）考试”&…...
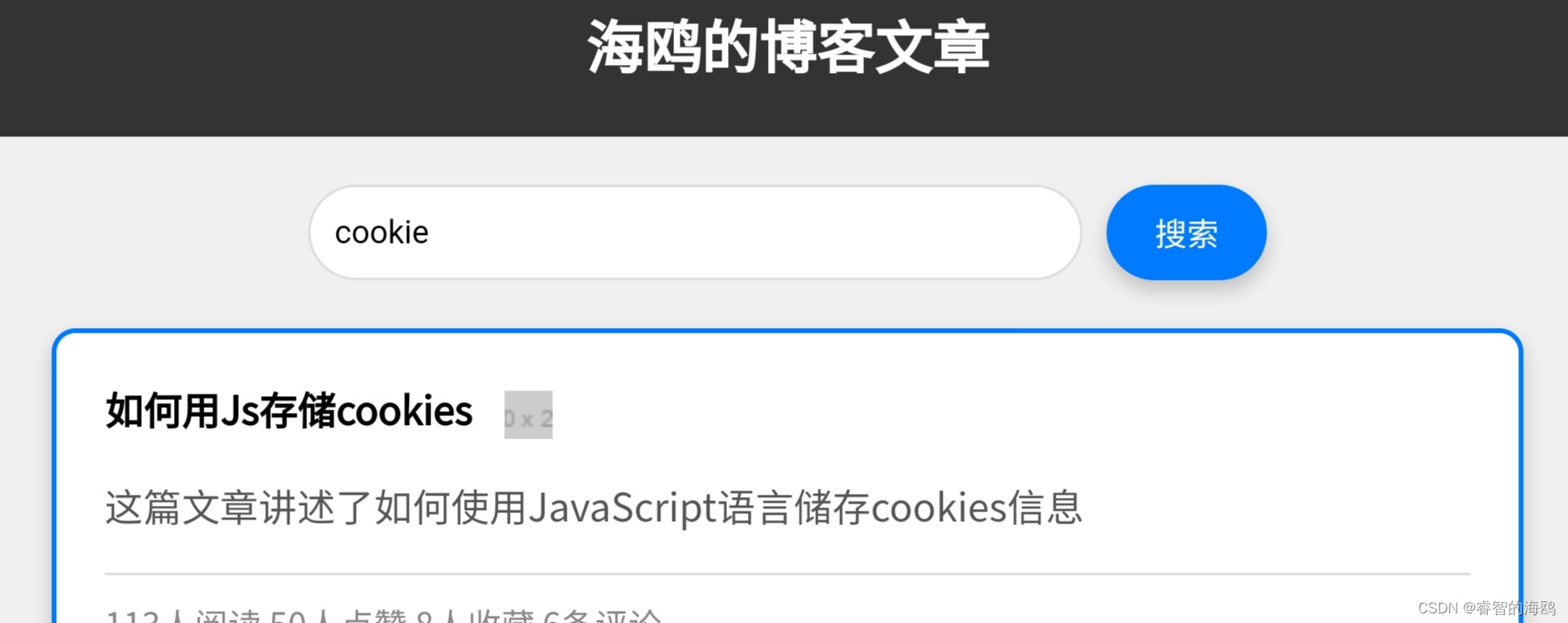
JS+H5美观的带搜索的博客文章列表（可搜索多个参数）
实现 美观的界面（电脑、手机端界面正常使用）多参数搜索（文章标题，文章简介，文章发布时间等）文章链接跳转 效果图 手机端 电脑端 搜索实现 搜索功能实现解释 定义文章数据: 文章数据保存在一个 JavaScri…...
)
牛客周赛 Round 54 (c++题解)
比赛地址 : 牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ A 输出o的个数； #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \n using namespace std; typedef long long LL;inlin…...
htsjdk库Genotype及相关类介绍
在 HTSJDK 库中，处理基因型的主要类包括 Genotype、FastGenotype、GenotypeBuilder 以及相关的类和接口。以下是这些类和接口的详细介绍： Genotype 类 主要功能 表示基因型：Genotype 类用于表示个体在特定变异位置上的基因型。基因型是对个体在变异位置上的等位基因组合的…...
C++ 最短路（spfa） 洛谷
拉近距离 题目背景 我是源点，你是终点。我们之间有负权环。 ——小明 题目描述 在小明和小红的生活中，有 N 个关键的节点。有 M 个事件，记为一个三元组 (Si,Ti,Wi)，表示从节点 Si 有一个事件可以转移到 Ti，事件…...
MySQL的数据类型
文章目录 数据类型分类整型bit类型浮点类型字符串类型charvarchar 日期和时间类型enum和set find_ in_ set 数据类型分类 整型 在MySQL中，整型可以指定是有符号的和无符号的，默认是有符号的。 可以通过UNSIGNED来说明某个字段是无符号的。 在MySQL中如…...
xss漏洞（四，xss常见类型）
本文仅作为学习参考使用，本文作者对任何使用本文进行渗透攻击破坏不负任何责任。 前言： 1，本文基于dvwa靶场以及PHP study进行操作，靶场具体搭建参考上一篇： xss漏洞（二，xss靶场搭建以及简单…...
繁简之争：为什么手机芯片都是 ARM
RISC 和 CISC 指令集 之前的文章《揭秘 CPU 是如何执行计算机指令的》中说到，如果从软件的角度来讲，CPU 就是一个执行各种计算机指令（Instruction Code）的逻辑机器。 计算机指令集是计算机指令的集合，包括各种类型的…...
【nnUNetv2进阶】十九、nnUNetv2 使用ResidualEncoder训练模型
nnunet使用及改进教程。 【nnUNetv2实践】一、nnUNetv2安装 【nnUNetv2实践】二、nnUNetv2快速入门-训练验证推理集成一条龙教程 【nnUNetv2进阶】三、nnUNetv2 自定义网络-发paper必会-CSDN博客 其他网络改进参考： 【nnUNetv2进阶】四、nnUNetv2 魔改网络-小试牛刀-加入…...
利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装（Encapsulation） 定义：将数据（属性）和操作数据的方法绑定在一起，通过访问控制符（private、protected、public）隐藏内部实现细节。示例： public …...
Zustand 状态管理库：极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库，特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
工程地质软件市场：发展现状、趋势与策略建议
一、引言 在工程建设领域，准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具，正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装： 下载安装DevEco Studio 4.0（支持HarmonyOS 5）配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化： ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
C++ 基础特性深度解析
目录 引言 一、命名空间（namespace） C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用（reference） C 中的引用 与 C 语言的对比 四、inline（内联函数…...
视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件，或者在构建过程中仍然引用了旧的路…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流：用一个简单脚本，秒杀视频片头广告，还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农，平时写代码之余看看电影、补补片，是再正常不过的事。 电影嘛，要沉浸，…...
day36-多路IO复用
一、基本概念 （服务器多客户端模型） 定义：单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用：应用程序通常需要处理来自多条事件流中的事件，比如我现在用的电脑，需要同时处理键盘鼠标…...
python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用： 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests：发送 …...