【文件系统】抽象磁盘的存储结构 CHS寻址法 | sector数组 | LAB数组
目录
1.为什么要抽象
2.逻辑抽象_版本1
2.1sector数组
2.2index转化CHS
3.逻辑抽象_版本2
3.1LBA数组
3.2LAB下标转化sector下标
- 文件其实就是在磁盘中占有几个扇区的问题❗
- 文件是很多个sector的数组下标❗
- 文件是有很多块构成的❗
- ❗文件由很多扇区构成------>文件由很多的index构成----->文件由很多的块构成
1.为什么要抽象
- 硬件的存储结构发生改变,OS软件随之发生变化。直接使用CHS的耦合度太高,不想软件直接拿着硬件的参数去访问。
- 为了后面编码设计,为了方便内核进行磁盘管理
- OS需要也需要对大量的磁盘文件管理❗
- 管理啊:先描述再组织❗
- 下面我们走一遍OS对磁盘这样的设备进行管理和抽象。
- OS对磁盘的管理转化成了对数组的管理,先描述再组织。
- 描述:描述成数字
- 组织:组织成数组
2.逻辑抽象_版本1
2.1sector数组
- 圆形结构变成了线性结构。磁盘抽象成线性结构。
- 线性结构的每一段都是一个扇区。
- 这个线性结构可以看成一个数组,数组元素是一个一个的扇区。
- 天然就存在一个东西:数组下标表示sector(相当于对扇区进行了编址)
 2.2index转化CHS
2.2index转化CHS
- OS是拿到下标index就可以访问扇区
- 硬件是使用CHS来进行扇区寻址
- 磁盘的每个盘面的容量大小一样(磁道数/扇区数是一样大小的)
- 二者的转化算法是很简单的,并且这个工作是磁盘内部完成的。
- index------>硬件电路------->磁盘内部转化-------->CHS地址--------->磁盘的硬件定位扇区
前提:已知 磁盘总容量和每个扇区的大小=扇区数,磁道数。
磁盘的每个盘面:有1000个扇区,10个磁道(每一个磁道都有100个扇区)
index / 扇区数 = 定位的盘面(H)
index % 扇区数 = tmp
tmp / 100 = 定位磁道(C)
tmp % 100 = 定位扇区(S)
3.逻辑抽象_版本2
3.1LBA数组
- 内存和外设之间进行IO交互。512字节会不会太小了。OS觉得有点小。(C语言访问内存是1字节,经常性是4/8字节访问)
- 站在硬件的角度:每次往内存拷贝加载数据,512字节。
- 站在OS的角度:效率低,能不能拷贝更多数据。可以4KB。
- 基本单位是:4KB(可以修改需要重新编译OS,大部分场景够用,一次性读8个扇区)
- ❗4KB的大小是规定出来的。有块号(规定)
- ❗OS:4KB = 8个连续的扇区 = 数据块(块大小)= 文件块
- 大页式内核:4MB
- 1KB = 1024字节


3.2LAB下标转化sector下标
- 逻辑区块地址(Logical Block Address, LBA)是描述计算机存储设备上数据所在区块的通用机制,一般用在像硬盘这样的辅助记忆设备。
- 8个扇区为1个块
- 块号✖8(一个块的扇区数)= 一个块的第一个扇区sector的下标
- 整个块的下标:第一个sector知道了,往后连续数7个就是这个块。01234567。每一个块的扇区的下标都知道了。再通过版本1的计算方法就可以知道CHS地址了。
- 对于OS而言,未来我们读取数据,可以以块为单位了❗磁盘可以看成很多的块。
- 只要知道第一个块号,就可以知道全部的块号了。(前提知道磁盘的总大小——总大小/4即可)只要知道一个起始,和磁盘的总大小,有多少块,每个块的块号,如何准换到对应的多个CHS地址,全部都知道了❗
- 总大小/4KB=总块数=块的编号LBA---------->每个块的第一个起始地址=sector的下标----------->每个块中全部的sector的下标--------->每个下标index通过计算得到CHS地址---------->定位到硬件里面的扇区。
相关文章:

【文件系统】抽象磁盘的存储结构 CHS寻址法 | sector数组 | LAB数组
目录 1.为什么要抽象 2.逻辑抽象_版本1 2.1sector数组 2.2index转化CHS 3.逻辑抽象_版本2 3.1LBA数组 3.2LAB下标转化sector下标 文件其实就是在磁盘中占有几个扇区的问题❗文件是很多个sector的数组下标❗文件是有很多块构成的❗❗文件由很多扇区构成------>文件…...

基于python旅游推荐系统(源码+论文+部署讲解等)
博主介绍:✌全网粉丝10W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行前辈交流✌ 技术栈介绍:我是程序员阿龙ÿ…...

Mysql大单表JSON优化
优化方案 MySQL 8.0.32 中,有几种方法可以优化存储 JSON 字符串的数据表。以下是一些建议,可以帮助您减少存储空间: 使用压缩: MySQL 8.0 支持表级压缩,可以通过修改表来启用压缩。 ALTER TABLE your_table ROW_FORMATCOMPRESS…...

电脑开机启动项管理小工具,绿色免安装
HiBit Startup Manager 是一款功能强大的启动项管理工具,旨在帮助用户管理和优化计算机的自动启动程序。该软件通过添加或删除应用程序、编辑它们的属性以及管理流程、服务、任务调度程序和上下文菜单来实现这一目标。 HiBit Startup Manager 提供了以下主要功能&a…...
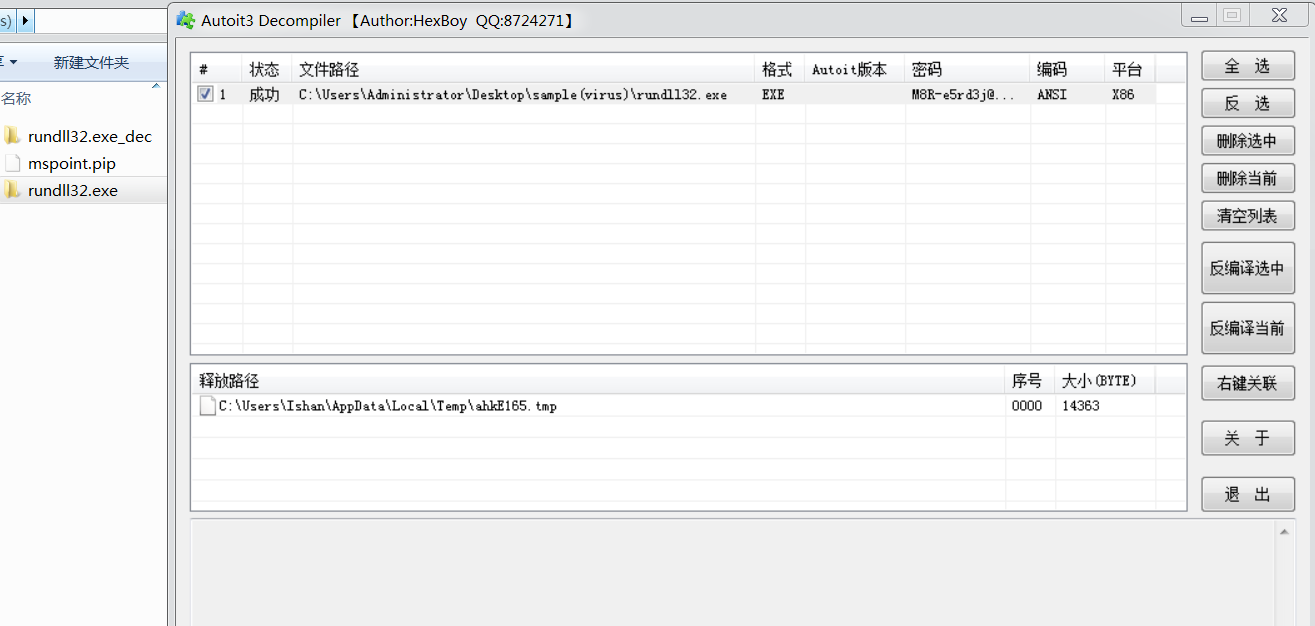
一例AutoHotkey语言生成的文件夹病毒分析
概述 这是一个使用AutoHotkey语言编写的文件夹病毒,使用ftp服务器来当作C2,通过U盘传播,样本很古老,原理也很简单,这种语言的样本还是第一次见到,记录一下。 样本的基本信息 PE32库: AutoIt(3.XX)[-]编译…...

【机器学习第7章——贝叶斯分类器】
机器学习第7章——贝叶斯分类器 7.贝叶斯分类器7.1贝叶斯决策论7.2 朴素贝叶斯分类器条件概率的m估计 7.3 极大似然估计优点基本原理 7.4 贝叶斯网络7.5 半朴素贝叶斯分类器7.6 EM算法7.7 EM算法实现 7.贝叶斯分类器 7.1贝叶斯决策论 一个医疗判断问题 有两个可选的假设&#…...

C++ QT开发 学习笔记(3)
C QT开发 学习笔记(3) - WPS项目 标准对话框 对话框类说明静态函数函数说明QFileDialog文件对话框getOpenFileName()选择打开一个文件getOpenFileNames()选择打开多个文件getSaveFileName()选择保存一个文件getExistingDirectory()选择一个己有的目录getOpenFileUrl()选择打幵…...

【Python实战】如何优雅地实现文字 二维码检测?
前几篇,和大家分享了如何通过 Python 和相关库,自动化处理 PDF 文档,提高办公效率。 【Python实战】自动化处理 PDF 文档,完美实现 WPS 会员功能【Python实战】如何优雅地实现 PDF 去水印?【Python实战】一键生成 PDF…...

行为型设计模式3:模板方法/备忘录/解释器/迭代器
设计模式:模板方法/备忘录/解释器/迭代器 (qq.com)...
思源笔记软件的优缺点分析
在过去一年里,我用了很多款笔记,从word文档到onenote到语雀再到思源,最后坚定的选择了思源笔记 使用感受 首先是用word文档来记笔记,主要是开始时不知道笔记软件怎么好用,等到笔记越来越膨胀的时候我发现,…...

追问试面试系列:Dubbo
欢迎来到Dubbo系列,在面试中被问到Dubbo相关的问题时,大部分都是简历上写了Dubbo,或者面试官想尝试问问你对Dubbo是否了解。 本系列主要是针对面试官通过一个点就使劲儿往下问的情况。 面试官:说说你们项目亮点 好的面试官 我们这个项目的技术亮点在于采用了Spring Cloud…...

动手学深度学习V2每日笔记(卷积层)
本文主要参考沐神的视频教程 https://www.bilibili.com/video/BV1L64y1m7Nh/p2&spm_id_from333.1007.top_right_bar_window_history.content.click&vd_sourcec7bfc6ce0ea0cbe43aa288ba2713e56d 文档教程 https://zh-v2.d2l.ai/ 本文的主要内容对沐神提供的代码中个人不…...

qcom ucsi probe
ucsi glink 注册一个ucsi 设备,和pmic glink进行通信,ucsi作为pmic glink的一个client。 lkml的patch https://lkml.org/lkml/2023/1/30/233 dtsi中一般会定义 qcom,ucsi-glink 信息,用于和驱动进行匹配 static const struct of_device_id …...

flask和redis配合
对于涉及数据提交的场景,比如更新用户信息,你可能会使用POST或PUT请求。但是,这些操作通常与直接从Redis缓存中检索数据不同,因为它们可能涉及到对后端数据库或其他存储系统的修改。并且可能需要将更新后的数据同步回Redis缓存&am…...

深度学习中的早停法
早停法(Early Stopping)是一种用于防止模型过拟合的技术,在训练过程中监视验证集(或者测试集)上的损失值。具体设立早停的限制包括两个主要参数: Patience(耐心):这是指验…...

科普文:JUC系列之多线程门闩同步器CountDownLatch的使用和源码
CountDownLatch类位于java.util.concurrent包下,利用它可以实现类似计数器的功能。比如有一个任务A,它要等待其他10个线程的任务执行完毕之后才能执行,此时就可以利用CountDownLatch来实现这种功能了。 CountDownLatch是通过一个计数器来实现…...

foreach循环和for循环在PHP中各有什么优势
在PHP中,foreach循环和for循环都是用来遍历数组的常用结构,但它们各有其优势和使用场景。 foreach循环的优势 简化代码:foreach循环提供了一种更简洁的方式来遍历数组,不需要手动控制索引或指针。易于阅读:对于简单的…...

巧用casaos共享挂载自己的外接硬盘为局域网共享
最近入手了个魔改机顶盒,已经刷好了的armbian,虽然是原生的,但是我觉得挺强大的,内置了很多 常用的docker和应用,只需要armbian-software 安装就行,缺点就是emmc太小了。 买到之后第一时间装上了casaos和1p…...

标题:解码“八股文”:助力、阻力,还是空谈?
标题:解码“八股文”:助力、阻力,还是空谈? 在程序员的面试与职场发展中,“八股文”一直是一个备受争议的话题。它既是求职者展示自己技术功底的途径,也是一些公司筛选人才的标准之一。但“八股文”在实际…...

语言无界,沟通无限:2024年好用在线翻译工具推荐
随着技术的发展现在的翻译在线工具从基础词句翻译到复杂的文章翻译都不在话下。为了防止你被五花八门的工具挑花眼,我给你介绍几款我用过的便捷、高效、准确的翻译工具吧。 1.福晰翻译端 链接直通:https://www.foxitsoftware.cn/fanyi/ 这个软件支持…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
