当前位置：首页 > news >正文

数据结构与算法 - 二叉树

news 2026/2/9 11:38:53

1. 概述

二叉树是这么一种树状结构：每个节点最多有两个孩子，左孩子和右孩子

完全二叉树：是一种二叉树结构，除了最后一层以外，每一层都必须填满，填充时要遵循从左到右

平衡二叉树：是一种二叉树结构，其中每个节点的左右子树高度相差不超过1

2. 存储

存储方式分为两种:

①定义树结点与左、右孩子引用（TreeNode）

②使用数组，若用0作为树的根节点，索引可以通过以下方式计算

父 = floor((子 - 1) / 2)
左孩子 = 父 * 2 + 1
右孩子 = 父 * 2 + 2

3. 遍历

遍历方式也分为两种：

①广度优先遍历：尽可能先访问距离根节点最近的节点，也称为层序遍历

②深度优先遍历：对于二叉树，可以进一步划分为三种（要深入到叶子节点）

pre-order前序遍历：对于每一棵子树，先访问该节点，然后是左子树，最后是右子树
in-order中序遍历：对于每一棵子树，先访问左子树，然后是该节点，最后是右子树
post-order后续遍历：对于每一棵子树，先访问左子树，然后是右子树，最后是该节点

3.1 广度优先遍历

本轮开始时队列	本轮访问节点
[1]	1
[2, 3]	2
[3, 4]	3
[4, 5, 6]	4
[5, 6]	5
[6, 7, 8]	6
[7, 8]	7
[8]	8
[]

1. 初始化，将根节点加入队列

2. 循环处理队列中每个节点，直至队列为空

3. 每次循环内处理节点后，将它的孩子节点（即下一层节点）加入队列

注意：

以上用队列来实现层序遍历是针对TreeNode这种方式表示的二叉树
对于数组实现的二叉树，则直接遍历数组即可，自然为层序遍历的顺序

3.2 深度优先遍历

栈暂存	已处理	前序遍历	中序遍历
[1]	1 ✔️ 左💤 右💤	1
[1, 2]	2✔️ 左💤 右💤 1✔️ 左💤 右💤	2
[1, 2, 4]	4✔️ 左✔️ 右✔️ 2✔️ 左💤 右💤 1✔️ 左💤 右💤	4	4
[1, 2]	2✔️ 左✔️ 右✔️ 1✔️ 左💤 右💤		2
[1]	1✔️ 左✔️ 右💤		1
[1, 3]	3✔️ 左💤 右💤 1✔️ 左✔️ 右💤	3
[1, 3, 5]	5✔️ 左✔️ 右✔️ 3✔️ 左💤 右💤 1✔️ 左✔️ 右💤	5	5
[1, 3]	3✔️ 左✔️ 右💤 1✔️ 左✔️ 右💤		3
[1, 3, 6]	6✔️ 左✔️ 右✔️ 3✔️ 左✔️ 右💤 1✔️ 左✔️ 右💤	6	6
[1, 3]	3✔️ 左✔️ 右✔️ 1✔️ 左✔️ 右💤
[1]	1✔️ 左✔️ 右✔️
[]

3.2.1 递归实现

/*** <h3>前序遍历</h3>* @param node 节点*/
static void preOrder(TreeNode node) {if (node == null) {return;}System.out.print(node.val + "\t"); // 值preOrder(node.left); // 左preOrder(node.right); // 右
}/*** <h3>中序遍历</h3>* @param node 节点*/
static void inOrder(TreeNode node) {if (node == null) {return;}inOrder(node.left); // 左System.out.print(node.val + "\t"); // 值inOrder(node.right); // 右
}/*** <h3>后序遍历</h3>* @param node 节点*/
static void postOrder(TreeNode node) {if (node == null) {return;}postOrder(node.left); // 左postOrder(node.right); // 右System.out.print(node.val + "\t"); // 值
}

3.2.2 非递归实现

前序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();  // 此处的LinkedListStack为自己实现的
TreeNode curr = root;while (!stack.isEmpty() || curr != null) {if (curr != null) {stack.push(curr);System.out.println(curr);curr = curr.left;} else {TreeNode pop = stack.pop();curr = pop.right;}}

中序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;while (!stack.isEmpty() || curr != null) {if (curr != null) {stack.push(curr);curr = curr.left;} else {TreeNode pop = stack.pop();System.out.println(pop);curr = pop.right;}
}

后序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;
TreeNode pop = null;while (!stack.isEmpty() || curr != null) {if (curr != null) {stack.push(curr);curr = curr.left;} else {TreeNode peek = stack.peek();if (peek.right == null || peek.right == pop) {pop = stack.pop();System.out.println(pop);} else {curr = peek.right;}}
}

对于后序遍历，向后走时，需要处理完右子树才能pop出栈。如何直到右子树处理完成呢？

①如果栈顶元素的 right == null ，表示没啥可处理的，可以出栈

②如果栈顶元素的 right != null

那么使用lastPop记录最近出栈的节点，即表示从这个节点向回走
如果栈顶元素 right == lastPop，此时应当出栈

对于前、中两种遍历，实际以上代码从右子树向回走时，并未走完全程（stack提前出栈了），而后序遍历以上代码是走完全程了。

统一写法（依据后序遍历修改）

LinkedList<TreeNode> stack = new LinkedList<>();TreeNode curr = root; // 代表当前节点
TreeNode pop = null; // 最近一次弹栈的元素
while (curr != null || !stack.isEmpty()) {if (curr != null) {colorPrintln("前: " + curr.val, 31);stack.push(curr); // 压入栈，为了记住回来的路curr = curr.left;} else {TreeNode peek = stack.peek();// 右子树可以不处理, 对中序来说, 要在右子树处理之前打印if (peek.right == null) {colorPrintln("中: " + peek.val, 36);pop = stack.pop();colorPrintln("后: " + pop.val, 34);}// 右子树处理完成, 对中序来说, 无需打印else if (peek.right == pop) {pop = stack.pop();colorPrintln("后: " + pop.val, 34);}// 右子树待处理, 对中序来说, 要在右子树处理之前打印else {colorPrintln("中: " + peek.val, 36);curr = peek.right;}}
}public static void colorPrintln(String origin, int color) {System.out.printf("\033[%dm%s\033[0m%n", color, origin);
}

一张图演示三种遍历

红色：前序遍历
绿色：中序遍历
蓝色：后序遍历

4. 习题

4.1 前序遍历二叉树

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

解法一：递归

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();preorderHelper(root, result);return result;}private void preorderHelper(TreeNode root, List<Integer> result) {if (root == null) {return;}result.add(root.val);preorderHelper(root.left, result);preorderHelper(root.right, result);}
}

解法二：迭代

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> preorderTraversal(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();List<Integer> result = new ArrayList<>();TreeNode curr = root;while (!stack.isEmpty() || curr != null) {if (curr != null) {stack.push(curr);result.add(curr.val);curr = curr.left;} else {TreeNode pop = stack.pop();curr = pop.right;}}return result;}
}

解法三：莫里斯遍历（Morris Traversal）

①莫里斯遍历的核心思想是通过利用树的空指针链接来避免使用栈

②对于每个节点，如果它的左子树为空，则访问当前节点并移动到右子树

③如果左子树不为空，找到当前节点的前驱节点（即左子树中最右的节点），检查它的右指针

如果它的右指针为空，则将其指向当前节点，并返回当前节点
如果它的右指针已经指向当前节点，说明左子树已经遍历结束，将右指针恢复为null，并移动到右子树。

时间复杂度：O(n)；空间复杂度：O(1)

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {  public List<Integer> preorderTraversal(TreeNode root) {  List<Integer> result = new ArrayList<>();  TreeNode curr = root;  while (curr != null) {  if (curr.left == null) {  // 访问当前节点  result.add(curr.val);  curr = curr.right; // 移动到右子树  } else {  // 找到当前节点的前驱节点  TreeNode pred = curr.left;  while (pred.right != null && pred.right != curr) {  pred = pred.right;  }  // 建立链接  if (pred.right == null) {  pred.right = curr; // 建立临时连接  result.add(curr.val); // 访问当前节点  curr = curr.left; // 移动到左子树  } else {  // 恢复树结构  pred.right = null;  curr = curr.right; // 移动到右子树  }  }  }  return result;  }  
}

4.2 中序遍历二叉树

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

解法一：递归

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderHelper(root, result);return result;}private void inorderHelper(TreeNode root, List<Integer> result) {if (root == null) {return;}inorderHelper(root.left, result);result.add(root.val);inorderHelper(root.right, result);}
}

解法二：迭代

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();List<Integer> result = new ArrayList<>();TreeNode curr = root;while (!stack.isEmpty() || curr != null) {if (curr != null) {stack.push(curr);curr = curr.left;} else {TreeNode pop = stack.pop();result.add(pop.val);curr = pop.right;}}return result;}
}

解法三：莫里斯算法

①莫里斯遍历的核心思想是通过利用树的空指针链接来避免使用栈

②对于每个节点，如果它的左子树为空，则访问当前节点并移动到右子树

③如果左子树不为空，找到当前节点的前驱节点（即左子树中最右的节点），检查它的右指针

如果它的右指针为空，则将其指向当前节点，并返回当前节点
如果它的右指针已经指向当前节点，说明左子树已经遍历结束，将右指针恢复为null，并移动到右子树。

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();TreeNode curr = root;while (curr != null) {if (curr.left == null) { // 左子树为空// 访问当前节点result.add(curr.val);// 移动到右子树curr = curr.right;} else {// 找到当前节点的前驱节点TreeNode pred = curr.left;while (pred.right != null && pred.right != curr) {pred = pred.right;}// 建立链接if (pred.right == null) {// 建立临时链接pred.right = curr;// 移动到左子树curr = curr.left;} else {// 恢复树结构pred.right = null;// 访问当前节点result.add(curr.val);// 移动到右子树curr = curr.right;}}}return result;}
}

4.3 后序遍历二叉树

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

解法一：递归

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();postOrderHelper(root, result);return result;}private void postOrderHelper(TreeNode root, List<Integer> result) {if (root == null) {return;}postOrderHelper(root.left, result);postOrderHelper(root.right, result);result.add(root.val);}
}

解法二：迭代

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> postorderTraversal(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();List<Integer> result = new ArrayList<>();TreeNode curr = root;TreeNode pop = null;while (!stack.isEmpty() || curr != null) {if (curr != null) {stack.push(curr);curr = curr.left;} else {TreeNode peek = stack.peek();if (peek.right == null || peek.right == pop) {pop = stack.pop();result.add(pop.val);} else {curr = peek.right;}}}return result;}
}

4.4 对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

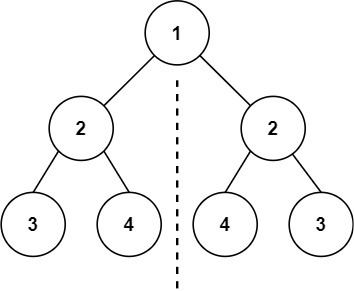
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

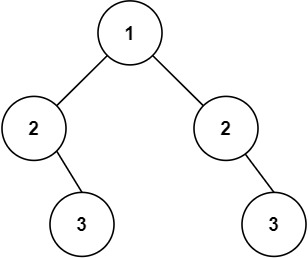
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

解法一：递归

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null) {return true;}return dfs(root.left, root.right);}private boolean dfs(TreeNode left, TreeNode right) {if(left == null && right == null) {return true;} if(left == null || right == null) {return false;}return (left.val == right.val) && dfs(left.left, right.right) && dfs(left.right, right.left);}
}

解法二：迭代

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {if (root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root.left);queue.offer(root.right);while (!queue.isEmpty()) {TreeNode leftNode = queue.poll();TreeNode rightNode = queue.poll();if (leftNode == null && rightNode == null) {  // 左右两个子树为空continue;}if (leftNode == null || rightNode == null) {  // 两边只有一个子树为空return false;}if (leftNode.val != rightNode.val) {return false;}queue.offer(leftNode.left);queue.offer(rightNode.right);queue.offer(leftNode.right);queue.offer(rightNode.left);}return true;}
}

4.5 二叉树最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

树中节点的数量在 [0, 10^4] 区间内。
-100 <= Node.val <= 100

解法一：递归

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;}
}

解法二：

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}Stack<Pair<TreeNode, Integer>> stack = new Stack<>();stack.push(new Pair<>(root, 1));int maxDepth = 0;while (!stack.isEmpty()) {Pair<TreeNode, Integer> current = stack.pop();TreeNode node = current.getKey();int depth = current.getValue();maxDepth = Math.max(depth, maxDepth);if (node.left != null) {stack.push(new Pair<>(node.left, depth + 1));}if (node.right != null) {stack.push(new Pair<>(node.right, depth + 1));}}return maxDepth;}
}

解法三：使用二叉树的非递归后序遍历，栈的最大高度即为最大深度

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {// 使用非递归后序遍历，栈的最大高度即为最大深度public int maxDepth(TreeNode root) {TreeNode curr = root;TreeNode pop = null;LinkedList<TreeNode> stack = new LinkedList<>();int max = 0; // 栈的最大高度while(curr != null || !stack.isEmpty()) {if(curr != null) {stack.push(curr);max = Integer.max(stack.size(), max);curr = curr.left;} else {TreeNode peek = stack.peek();if(peek.right == null || peek.right == pop) {pop = stack.pop();} else {curr = peek.right;}}}return max;}
}

解法四：二叉树的层序遍历，层数即最大深度

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {int size = queue.size();for (int i = 0; i < size; i++) {TreeNode poll = queue.poll();if (poll.left != null) {queue.offer(poll.left);}if (poll.right != null) {queue.offer(poll.right);}}depth++;}return depth;}
}

4.6 二叉树最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 10^5] 内
-1000 <= Node.val <= 1000

解法一：层序遍历。遇到第一个叶子节点所在层数即为最小深度

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int minDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 1;while (!queue.isEmpty()) {int size = queue.size();for (int i = 0; i < size; i++) {TreeNode node = queue.poll();if (node.left == null && node.right == null) {return depth;}if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}depth++;}return depth;}
}

解法二：后序遍历

相较于求最大深度，应当考虑：

当右子树为null，应当返回左子树深度加一
当左子树为null，应当返回右子树深度加一

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int minDepth(TreeNode node) {if (node == null) {return 0;}int d1 = minDepth(node.left);int d2 = minDepth(node.right);if (d1 == 0 || d2 == 0) {return d1 + d2 + 1;}return Integer.min(d1, d2) + 1;}
}

4.7 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100

解法一：递归

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {reverse(root);return root;}private void reverse(TreeNode node) {if(node == null) {return;}TreeNode t = node.left;node.left = node.right;node.right = t;reverse(node.left);reverse(node.right);}
}

或

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {if(root == null) {return null;}// 递归翻转左右子树TreeNode left = invertTree(root.left);TreeNode right = invertTree(root.right);// 交换左右子树// TreeNode t = root.left;root.left = root.right;root.right = left;return root;}
}

4.8 后缀表达式转二叉树

遇到运算符，则出栈两次，将出栈元素与当前节点建立父子关系，当前节点入栈
遇到数字则入栈

    public TreeNode constructExpressionTree(String[] tokens) {LinkedList<TreeNode> stack = new LinkedList<>();for (String token : tokens) {switch (token) {// 遇到运算符，出栈两次，与当前节点建立父子关系，将当前节点入栈case "+", "-", "*", "/" -> {TreeNode right = stack.pop();TreeNode left = stack.pop();TreeNode parent = new TreeNode(Integer.parseInt(token));parent.left = left;parent.right = right;stack.push(parent);}default -> {  // 遇到数字入栈stack.push(new TreeNode(Integer.parseInt(token)));}}}return stack.peek();}

4.9 根据前序与中序遍历结果构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

解法一：

先通过前序遍历结果定位根节点
再结合中序遍历结果切分左右子树

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {Map<Integer, Integer> indexMap = new HashMap<>();for (int i = 0; i < inorder.length; i++) {indexMap.put(inorder[i], i);}return buildTreeHelper(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1, indexMap);}private TreeNode buildTreeHelper(int[] preorder, int[] inorder, int preStart, int preEnd, int inStart, int inEnd,Map<Integer, Integer> indexMap) {if (preStart > preEnd || inStart > inEnd) {return null;}int rootVal = preorder[preStart]; // 根节点的位置TreeNode root = new TreeNode(rootVal);int inIndex = indexMap.get(rootVal);int leftSubtreeSize = inIndex - inStart; // 左子树root.left = buildTreeHelper(preorder, inorder, preStart + 1, preStart + leftSubtreeSize, inStart, inIndex - 1,indexMap);root.right = buildTreeHelper(preorder, inorder, preStart + leftSubtreeSize + 1, preEnd, inIndex + 1, inEnd,indexMap);return root;}
}

4.10 根据中序与后序遍历结果构造二叉树

解法一：

先通过后序遍历结果定位根节点
再结合中序遍历结果划分左右子树

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {Map<Integer, Integer> indexMap = new HashMap<>();for (int i = 0; i < inorder.length; i++) {indexMap.put(inorder[i], i);}return buildTreeHelper(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1, indexMap);}private TreeNode buildTreeHelper(int[] inorder, int[] postorder, int inStart, int inEnd, int postStart, int postEnd,Map<Integer, Integer> indexMap) {if (inStart > inEnd || postStart > postEnd) {return null;}int rootVal = postorder[postEnd]; // 根节点的位置TreeNode root = new TreeNode(rootVal);int inIndex = indexMap.get(rootVal);int rightSubtreeSize = inEnd - inIndex; // 右子树root.left = buildTreeHelper(inorder, postorder, inStart, inIndex - 1, postStart, postEnd - rightSubtreeSize - 1,indexMap);root.right = buildTreeHelper(inorder, postorder, inIndex + 1, inEnd, postEnd - rightSubtreeSize, postEnd - 1,indexMap);return root;}
}

数据结构与算法 - 二叉树

1. 概述二叉树是这么一种树状结构：每个节点最多有两个孩子，左孩子和右孩子完全二叉树：是一种二叉树结构，除了最后一层以外，每一层都必须填满，填充时要遵循从左到右平衡二叉树：是一种二叉树…...

编程日记 2024/8/5 10:41:23

Spring Cloud Gateway如何给一个请求加请求头

在Spring Cloud Gateway中，可以通过编写一个GlobalFilter来给所有请求加请求头，或者通过编写一个SpecificFilter来给特定路径的请求加请求头。全局过滤器（GlobalFilter）的实现方式如下： Configuration public class…...

编程日记 2024/8/5 10:39:19

chromedriver版本下载地址汇总chromedriver所有版本下载地址汇总国内源下载

谷歌浏览器版本经常会升级，chromedriver 也得下载匹配的版本 chromedriver 114以前版本下载地址https://registry.npmmirror.com/binary.html?pathchromedriver/ windows版本请访问链接：https://blog.csdn.net/FL1768317420/article/details/139712108 …...

编程日记 2024/8/5 10:38:17

Go语言与Windows系统

1.获取屏幕尺寸源自：Golang通过使用GetSystemMetrics获取系统的分辨率 - 完美代码 (perfcode.com) package mainimport ("syscall""fmt" )const (SM_CXSCREEN uintptr(0) // X Size of screenSM_CYSCREEN uintptr(1) // Y Size of screen …...

编程日记 2024/8/5 10:36:14

JAVA—面向对象编程高级

学习了一定基础后，开始更加深入的学习面向对象，包含static,final两个关键字，面向对象编程三大特征之继承和多态。以及对于抽象类，内部类，接口，枚举，泛型的学习。目录 1.static （…...

编程日记 2024/8/5 10:35:13

[BJDCTF2020]Mark loves cat1

打开题目发现这么多链接，以为要一点点去找功能上的漏洞。当你源代码，dirsearch，抓包等等操作之后，发现什么都没有。所以这题又是一道源码泄露题，上GItHack。扫描结果如下 http://63f29a80-e08b-43ae-a6d0-8e70fb02ea…...

编程日记 2024/8/5 10:34:12

微信答题小程序产品研发-用户操作流程设计

在答题小程序中，用户流程是指用户从进入小程序开始，到完成答题、查看结果、进行练习等一系列操作的步骤。这里我画了一张用户流程图，展示用户在小程序中的主要操作流程。以及对每个步骤的详细说明。这里分两种角色，用户和管理员…...

编程日记 2024/8/5 10:33:10

目标检测——YOLOv10: Real-Time End-to-End Object Detection

YOLOv10是在YOLOv8的基础上，借鉴了RT-DETR的一些创新点改进出来的标题：YOLOv10: Real-Time End-to-End Object Detection论文：https://arxiv.org/pdf/2405.14458源码：https://github.com/THU-MIG/yolov10 1. 论文介绍在过去的几…...

编程日记 2024/8/5 10:30:06

堡垒机简单介绍

堡垒机（Bastion Host），也被称为跳板机、跳板服务器或堡垒服务器，是一种在网络安全中扮演重要角色的设备或服务。以下是关于堡垒机的详细介绍： 一、定义与功能堡垒机是一种用于控制和管理网络安全的重要工具&#xf…...

编程日记 2024/8/5 10:29:05

【星闪开发连载】WS63E 星闪开发板和hi3861开发板的对比

此次星闪开发者体验官活动使用的开发板都是NearLink_DK_WS63E开发板，它和NearLink_DK_WS63开发板的区别在于具有雷达感知功能。从开发板的照片也可以看到WS63E有一个雷达天线接口。我们把WS63E开发板和hi3861开发板的功能做了简单的对比，见下表。参数…...

编程日记 2024/8/5 10:28:03

Python接口自动化测试框架（实战篇）-- Jenkins持续集成

文章目录一、前言二、[Jenkins](https://www.jenkins.io/)2.1、环境搭建2.2、插件准备2.3、创建job2.4、小结2.5、构建策略2.6、报告展示2.7、扩展三、总结一、前言温馨提示：在框架需要集成jenkins的时候，一定要注意环境切换问题，如果jenkins和开发环境是同样的系统且都有…...

编程日记 2024/8/5 10:27:02

【leetcode】根据二叉树创建字符串、二叉树的前中后遍历（非递归链表实现二叉树）

Hi~！这里是奋斗的明志，很荣幸您能阅读我的文章，诚请评论指点，欢迎欢迎 ~~ 🌱🌱个人主页：奋斗的明志 🌱🌱所属专栏：数据结构、LeetCode专栏 📚本系…...

编程日记 2024/8/5 10:26:00

【RabbitMQ】RabbitMQ交换机概述

一、交换机的类型 RabbitMQ提供了以下四种主要类型的交换机： 直连交换机（Direct Exchange） 特点：直连交换机是最基本的交换机类型，它根据完全匹配的路由键（Routing Key）将消息路由到绑定的队列…...

编程日记 2024/8/5 10:21:53

ROS2从入门到精通4-6：路径平滑插件开发案例(以B样条曲线平滑为例)

目录 0 专栏介绍1 ROS2路径平滑器介绍2 平滑器插件编写模板2.1 构造平滑器插件类2.2 注册并导出插件2.3 编译与使用插件 3 基于B样条曲线的路径平滑 0 专栏介绍本专栏旨在通过对ROS2的系统学习，掌握ROS2底层基本分布式原理，并具有机器人建模和应用ROS2…...

编程日记 2024/8/5 10:20:52

Tensorflow训练视觉模型（CPU）

目录零、模型下载一、清理C盘二、配置环境三、运行项目前提操作 （1）根据自己的项目设置路径。每次激活虚拟环境（tensorflow115）都得重设一次 （2）执行setup 这个项目的路径移动了位置也需要重设一…...

编程日记 2024/8/5 10:18:50

从根儿上学习spring 十之run方法启动第四段(4)

我们接着上一节已经准备开始分析AbstractAutowireCapableBeanFactory#doCreateBean方法，该方法是spring真正开始创建bean实例并初始化bean的入口方法，属于核心逻辑，所以我们新开一节开始分析。图12 图12-530到536行这几行的主要就是创建b…...

编程日记 2024/8/5 10:16:48

如果我的发明有修改，需要如何处理？

如果我的发明有修改，需要如何处理？...

编程日记 2024/8/5 10:15:47

java：File与MultipartFile互转

1 概述当我们在处理文件上传的功能时，通常会使用MultipartFile对象来表示上传的文件数据。然而，有时候我们可能已经有了一个File对象，而不是MultipartFile对象，需要将File对象转换为MultipartFile对象进行进一步处理。在Java中…...

编程日记 2024/8/5 10:11:43

高级java每日一道面试题-2024年8月04日-web篇-如果客户端禁止cookie能实现session还能用吗?

如果有遗漏,评论区告诉我进行补充面试官: 如果客户端禁止cookie能实现session还能用吗? 我回答: 当客户端禁用了Cookie时，传统的基于Cookie的Session机制会受到影响，因为Session ID通常是通过Cookie在客户端和服务器之间传递的。然而，尽…...

编程日记 2024/8/5 10:10:40

leetcode 107.二叉树的层序遍||

1.题目要求: 给你二叉树的根节点 root ，返回其节点值自底向上的层序遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）2.此题步骤: 1.先创建好队列，出队和入队函数: //创建队列 typedef struct que…...

编程日记 2024/8/5 10:09:38

Vim 调用外部命令学习笔记

Vim 外部命令集成完全指南文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令范围操作示例指定行范围处理复合命令示例实用技…...

编程新知 2025/11/16 8:24:16

TDengine 快速体验（Docker 镜像方式）

简介 TDengine 可以通过安装包、Docker 镜像及云服务快速体验 TDengine 的功能，本节首先介绍如何通过 Docker 快速体验 TDengine，然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker，请使用安装包的方式快…...

编程新知 2026/2/8 20:41:53

golang循环变量捕获问题

在 Go 语言中，当在循环中启动协程（goroutine）时，如果在协程闭包中直接引用循环变量，可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下： 问题背景看这个代码片段： fo…...

编程新知 2026/1/21 14:29:57

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序

一、开发环境准备工具安装： 下载安装DevEco Studio 4.0（支持HarmonyOS 5）配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化： ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

编程新知 2026/2/1 4:17:33

QT： `long long` 类型转换为 `QString` 2025.6.5

在 Qt 中，将 long long 类型转换为 QString 可以通过以下两种常用方法实现： 方法 1：使用 QString::number() 直接调用 QString 的静态方法 number()，将数值转换为字符串： long long value 1234567890123456789LL; …...

编程新知 2026/2/1 6:30:04

大数据学习（132）-HIve数据分析

🍋🍋大数据学习🍋🍋 🔥系列专栏： 👑哲学语录: 用力所能及，改变世界。 💖如果觉得博主的文章还不错的话，请点赞👍收藏⭐️留言&#x1f4…...

编程新知 2025/10/7 8:52:21

C++使用 new 来创建动态数组

问题： 不能使用变量定义数组大小原因： 这是因为数组在内存中是连续存储的，编译器需要在编译阶段就确定数组的大小，以便正确地分配内存空间。如果允许使用变量来定义数组的大小，那么编译器就无法在编译时确定数组的大…...

编程新知 2026/2/2 18:33:19

探索Selenium：自动化测试的神奇钥匙

目录一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

编程新知 2025/11/19 18:06:51

Monorepo架构: Nx Cloud 扩展能力与缓存加速

借助 Nx Cloud 实现项目协同与加速构建 1 ） 缓存工作原理分析在了解了本地缓存和远程缓存之后，我们来探究缓存是如何工作的。以计算文件的哈希串为例，若后续运行任务时文件哈希串未变，系统会直接使用对应的输出和制品文件。 2 …...

编程新知 2025/12/15 8:20:48

Python常用模块：time、os、shutil与flask初探

一、Flask初探 & PyCharm终端配置目的：快速搭建小型Web服务器以提供数据。工具：第三方Web框架 Flask (需 pip install flask 安装)。安装 Flask：建议：使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装，避免频繁切换。 PyCharm Terminal 配置建议：打开 Py…...

编程新知 2026/2/7 9:52:39

1. 概述

2. 存储

3. 遍历

3.1 广度优先遍历

3.2 深度优先遍历

3.2.1 递归实现

3.2.2 非递归实现

4. 习题

4.1 前序遍历二叉树

4.2 中序遍历二叉树

4.3 后序遍历二叉树

4.4 对称二叉树

4.5 二叉树最大深度

4.6 二叉树最小深度

4.7 翻转二叉树

4.8 后缀表达式转二叉树

4.9 根据前序与中序遍历结果构造二叉树

4.10 根据中序与后序遍历结果构造二叉树

相关文章：