河工院首届工业设计大赛程序组(挑战赛)题解
更好的阅读体验 \huge{\color{red}{更好的阅读体验}} 更好的阅读体验
寻找ACMer
思想:
- 签到题
- 按照题意遍历字符串,不断向后寻找包含 ACMer 完整字符串的数量即可
std标程:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);void solve(){string s; cin >> s;int idx = 0;int ans = 0;while(s.find("ACMer", idx) != -1) {ans ++; idx = s.find("ACMer", idx) + 1;}cout << ans << endl;}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
欧拉幻树苗
思想:
- 树形DP
- 始化每一个节点为独立的连通分量,即每个节点自身就是一个树的根。
- 读取树的结构,确保我们可以通过 g 数组访问到每个节点的孩子节点。
- 读取特殊边,并使用并查集合并特殊边的两个端点。由于题目保证特殊边的两个端点深度相同,合并这些端点不会导致环的出现。
- 然后开始广度优先搜索。从根节点(节点1)开始,用队列来记录接下来需要访问的节点。
- 对于当前节点 t,如果它是叶子,将 find(t) 的路径数加到答案中(即cnt[find(t)]),因为从叶子节点可以直接走到根节点。
- 遍历当前节点t的所有孩子节点,将父节点到当前节点的路径数累加到孩子节点上(需要通过find函数找到孩子节点所在的连通分量),然后将这些孩子节点加入队列中以进行下一轮搜索。
- 当队列为空时,所有节点都被访问过,搜索结束。最后输出计算的答案 ans。
std标程:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);int f[N], cnt[N]; // f数组用于并查集,cnt数组用于记录路径数vector<int> g[N]; // g数组用来存储树的结构int find(int x){return f[x] == x ? x : f[x] = find(f[x]);
}void solve() {int n, m; cin >> n >> m;for(int i = 1; i <= n; i ++) f[i] = i; // 初始化for(int i = 1; i < n; i ++){int x, y; cin >> x >> y; // 读取树的结构g[y].push_back(x); // 假设每条边是从子节点指向父节点}for(int i = 1; i <= m; i ++){int x, y; cin >> x >> y; // 输入特殊边f[find(x)] = find(y); // 合并特殊边的端点}queue<int> q;q.push(1);cnt[1] = 1; // 根节点的路径数为1int ans = 0; // 结果变量while(!q.empty()){int t = q.front();q.pop();if(g[t].empty()) (ans += cnt[find(t)]) %= mod; // 如果t是叶子节点,累加路径数for(auto i:g[t]){(cnt[find(i)] += cnt[find(t)]) %= mod; // 将当前节点的路径数累加到其孩子节点q.push(i); // 将孩子节点加入队列}}cout << ans;
}int main(){IOS;int _ = 1;//cin >> _;while(_ --){solve();}return 0;
}
疯狂蓝桥杯
本题主要考察四舍五入,C语言中是四舍六入,但是需要四舍五入,则在结果后面加上0.001即可。
std标程:
#include<bits/stdc++.h>using namespace std;
#define int long long
signed main()
{int T;cin>>T;while(T--){int n,m,x,y;cin>>n>>m>>x>>y;int z=n*y,zz=m*x;int zzz=z*zz/__gcd(z,zz);int i=zzz/z,j=zzz/zz;double s=sqrt(n*n*i*i+m*m*j*j) * 2; s+=0.001;printf("%.2lf\n",s);} return 0;
}
Inception Ⅰ
用数组(如st)记录每个数字出现的次数,从1枚举到 (m + 1)/ 2 (不含),所有 st[i] * st[m - i]的和,注意要开long long~
std标程:
#include <iostream>using namespace std;const int N = 1e6 + 20;
int n, m, st[N];
long long ans;int main()
{int x;cin >> n >> m;for(int i = 1; i <= n; i ++){cin >> x;st[x] ++;}for(int i = 0; i < m - i; i ++){ans += (long long)st[i] * st[m - i];}cout << ans;return 0;
}
Inception Ⅱ
循环枚举判断是否存在连续三个字母/四个元素组成的回文数组,(易证所有长度大于2的回文都包含这两种回文之一),定义数组记录下标为 i 的元素向后找最近的回文数组右端点的距离,如 1 1 2 2 1,对应记录数组应为 4,3,0,0,0。对每次查找的时间复杂度缩小到O(1)。
std标程:
#include <iostream>using namespace std;const int N = 1e6 + 20;
int n, q[N], s[N];int main()
{int t;scanf("%d %d", &n, &t);for (int i = 1; i <= n; i ++){scanf("%d", &q[i]);}for (int i = 1; i <= n; i ++){//偶数回文if (i + 3 <= n){if(q[i] == q[i + 3] && q[i + 1] == q[i + 2]) s[i] = 3;}//奇数回文if (i + 2 <= n){if (q[i] == q[i + 2]) s[i] = 2;}}int f = 0;for (int i = n; i > 0; i --){if (s[i] && !f) f = 1;if (f && !s[i]) s[i] = s[i + 1] + 1;}int l, r;while(t --){scanf("%d %d", &l, &r);if (!s[l]) printf("NO\n");else if (l + s[l] <= r) printf("YES\n");else printf("NO\n");}return 0;
}
Inception Ⅲ
易证,当 n == 1 或 n == 2 时,图腾陀螺可一步取胜,除此之外,Belinra均可胜利(想什么呢,这可是Belinra的主场,给你先手是客套,怎么可能让你轻易取胜)
std标程:
#include <iostream>using namespace std;int main()
{int n; cin >> n;if (n == 1 || n == 2) cout << "None life is but a dream .";else cout << "Wake up now !";return 0;
}
憧憬成为AK大神
思想:
- 贪心
- 有题目可知,到了某一个点都不能可能再往回走(回头一定不是最优解,否则在原来就已经进去AK了)
- 先对页面编号排序,然后用一个大根堆来维护从起始页面切换到当前这个页面的已AK的场次所消耗的时间
- 如果所有的时间消耗(切换界面的时间+对应场次让出的时间)已大于规定的时间,则该方向上的时间不可避免
- 所以只能少切换界面,因为每一场比赛都AK一次,即将让出时间最大的页面跳过即可
std标程:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);priority_queue<LL> q;PLL a[N];bool cmp(PLL &a, PLL b) {return a.fi < b.fi;
}LL n, m, ans, res, sum, idx;void solve(){cin >> n >> m;for (int i = 0; i <= n; i ++) {LL x, y; cin >> x >> y;a[++ idx].fi = x;a[idx].se = y;}sort(a + 1, a + n + 1, cmp);for(int i = 1; i <= n; i ++) {res += a[i].fi - a[i - 1].fi; //切换到 i 页面所用时间 q.push(a[i].se); // sum 的欲望 sum ++;res += a[i].se;while(!q.empty() && res > m) //如果用的时间多于m,直接ak掉 {sum --;res -= q.top();q.pop();}if(res > m) break; ans = max(ans, sum); }cout << ans << endl;
}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
高精度拼接
由于每添加一个数都需要满足 a % b == 0,故第一次从 0 到 9 枚举,如果存在满足条件的数直接输出即可,紧接着输出 n - 1 个 0,否则输出 -1
std标程:
#include <stdio.h>int main()
{int a, b, c, ans = -1;scanf("%d %d %d", &a, &b, &c);for (int i = 0; i <= 9; i ++){if ((a * 10 + i) % b == 0){ans = a * 10 + i;break;}}if (ans != -1){printf("%d", ans);for (int i = 1; i <= c - 1; i ++)printf("0");}else{printf("-1");}return 0;
}
逆矩阵
- 签到题,模拟
std标程:
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>using namespace std;#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);void solve(){int n; cin >> n;int size = n;n *= n;vector<vector<int>> ans(size, vector<int>(size, 0));int num = 1;int top = 0, st = size - 1, left = 0, right = size - 1;while(num <= n) {for(int i = top; i <= st && num <= n; i++) {ans[i][left] = num++;}left++; for(int i = left; i <= right && num <= n; i++) {ans[st][i] = num++;}st--;for(int i = st; i >= top && num <= n; i--) {ans[i][right] = num++;}right--;for(int i = right; i >= left && num <= n; i--) {ans[top][i] = num++;}top++;}for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {if (ans[i][j] != 0) {cout << ans[i][j] << " ";}}cout << endl;}
}int main(){IOS;int _ = 1;// cin >> _;while(_ --){solve();}return 0;}
相关文章:
题解)
河工院首届工业设计大赛程序组(挑战赛)题解
更好的阅读体验 \huge{\color{red}{更好的阅读体验}} 更好的阅读体验 寻找ACMer 思想: 签到题按照题意遍历字符串,不断向后寻找包含 ACMer 完整字符串的数量即可 std标程: #include <iostream> #include <cstring> #include …...

文件上传漏洞(二,靶场搭建及漏洞利用)
前言: 本文基于github上的upload-labs,PHP study以及bp抓包软件进行操作。 一,靶场搭建。 靶场链接 1,下载zip文件到PHP study下的www文件夹内,并解压。 2,创建网站。 此处php版本应选择较老版本&…...

大厂面试题分享第二期
大厂面试题分享第二期 如果执行了一条命令,"select count(*)from…",使用哪个引擎更快,为什么?垃圾回收器 CMS 和 G1的区别介绍一下CMS和G1CMS(并发)垃圾收集器G1垃圾回收器 HTTPS和HTTP的区别主…...

zabbix安装
a.安装 Zabbix 仓库 # rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/x86_64/zabbix-release-5.0-1.el7.noarch.rpm # yum clean all b. 安装 Zabbix server、前端、agent # yum install zabbix-server-mysql zabbix-agent c. 安装Zabbix前端 启用红帽软件集合 # …...

SpringBoot集成日志框架
SpringBoot集成日志框架 Java生态体系日志框架介绍 简介 在Java生态体系中,围绕着日志,有很多成熟的解决方案。关于日志输出,主要有两类工具。 一类是日志框架(Log4j、Logback),主要用来进行日志的输出的…...

CSS笔记总结(Xmind格式):第三天
Xmind鸟瞰图: 简单文字总结: css知识: 边框线: 1.border-width:边框的粗细 2.border-style:边框线的样式(solid实线,double双实线,dotted点线,dashed虚线) 3.border-color:边框线的颜色 4.简写形式&a…...

WordPress原创插件:Keyword-ranking-seo 1.0 关键词排名插件 有利于seo
WordPress原创插件:Keyword-ranking-seo 1.0 关键词排名插件 有利于seo 当用户访问网站时,该链接会随机选择一个关键词,并使用选定的搜索引擎进行搜索。 插件下载链接 https://download.csdn.net/download/huayula/89632792...

Docker Swarm 管理
Docker Swarm 是 Docker 提供的一种用于管理容器集群的工具。一、Docker Swarm 的主要特点包括: 高可用性:可以自动检测和恢复故障节点,确保服务的持续可用性。 例如,当某个工作节点出现故障时,Swarm 会将其上的任务重…...

跨平台、多格式、云同步,Koodo Reader背后的技术亮点
前言 对于像我这样的书虫来说,能够找到一个既方便又舒适的阅读环境,简直就是人生中的一大幸事;今天,就让小江湖我带你走进一个不一样的阅读世界——Koodo Reade! 无论是在喧嚣的都市,还是在宁静的乡村&a…...

【Story】如何高效记录并整理编程学习笔记?
目录 一、为何笔记在编程学习中如此重要?1.1 知识的捕捉1.2 理解和消化1.3 知识的复习1.4 知识的分享 二、建立高效的笔记系统2.1 确定笔记的目标2.2 选择合适的工具2.3 笔记的结构化2.4 记录有效的内容2.5 定期回顾和更新 三、保持笔记条理性的技巧3.1 使用一致的格…...
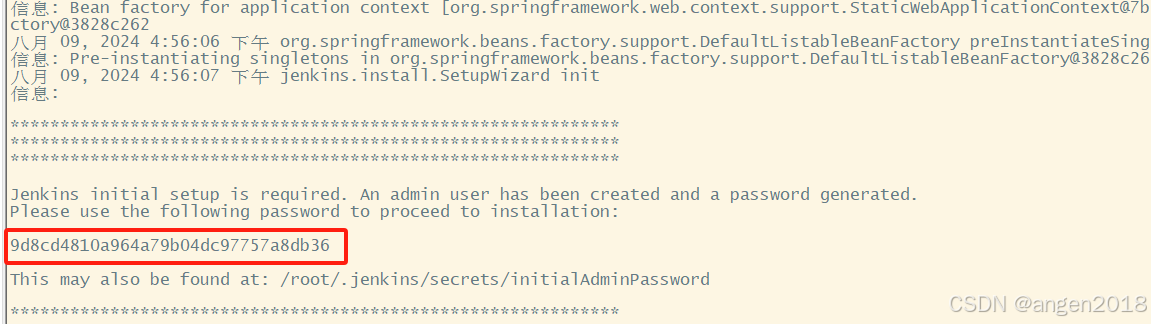
jenkins 安装以及自动构建maven项目并且运行
在这里找到你对应jdk的版本的jenkins包 War Jenkins Packages 我这里用的使java8,所以下载 https://mirrors.jenkins.io/war-stable/2.60.1/jenkins.war 然后jenkins可以安装到centos系统 在本地windows系统运行命令行 scp C:\Users\98090\Downloads\jenkins.war root@192…...

Java虚拟机:虚拟机介绍
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 033 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...
硬件面试经典 100 题(31~40 题)CRE4
31、多级放大电路的级间耦合方式有哪几种?哪种耦合方式的电路零点偏移最严重?哪种耦合方式可以实现阻抗变换? 有三种耦合方式:直接耦合、阻容耦合、变压器耦合。直接耦合的电路零点漂移最严重,变压器耦合的电路可以实现…...

ReactNative笔记(自用)
环境 ios更换gem镜像源: 查看当前源: gem sources -l 移除默认源: gem sources --remove https://rubygems.org/。添加新的源: 添加 Ruby China 的镜像源: gem source -a https://gems.ruby-china.com/或者添加其他镜像源。 清华大学的gem源: htt…...
)
嵌入式八股-面试30题(20240812)
TCP和UDP的区别是什么? **TCP(Transmission Control Protocol)**是面向连接的协议,提供可靠的、顺序的数据传输。它通过三次握手建立连接,并在数据传输过程中使用确认和重传机制来确保数据的正确性。TCP还支持流量控制和拥塞控制…...
)
单一职责原则(SRP)
目录 1、定义 2、优点 3、原则的重要性 4、 示例 5、注意事项 单一职责原则(Single Responsibility Principle, SRP)是面向对象设计中的一项重要原则,属于 SOLID 原则之一。它的核心思想是:一个类应该只有一个引起它变化的原因&am…...

骨传导耳机怎么选?分享五款资深用户都说好的骨传导耳机!
在追求健康生活的道路上,运动健身已成为一种时尚潮流,而音乐则是这场潮流中不可或缺的催化剂。然而,传统耳机在运动场景下的局限性日益凸显,难以满足运动者对自由与舒适的双重追求。正是基于这样的市场需求,骨传导耳机…...

【计算机网络——分组延时,丢失,吞吐量】
处理延时:1检查分组首部信息,决定将该分组导向何处所需时间。2检查比特级别的差错所需时间:分析这个分组是否出错,目标IP地址字段提取出来,查路由表……。 传播延时和传输延时:传输延时就是分组到链路所需…...

使用1panel 申请证书配置雷池站点
1.创建测试站点 2.使用1panel申请测试站点的自签名证书 ps:雷池支持自签的证书 关于如果选择网站的SSL证书 百度搜索 看起来是证书的问题 调整了参数重新申请一个证书上传 注意,如果文件上传错了,雷池会报错,如下图 再次访问配…...

4章7节:用R做数据重塑,数据去重和数据的匹配
在数据科学的分析流程中,数据重塑是一项非常重要的操作。数据的重塑通常指将数据从一种形式转换为另一种形式,以满足后续分析的需求。R语言提供了丰富的工具和函数来帮助用户高效地进行数据重塑操作。本文中,我们将深入探讨数据重塑的概念及其…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
