探索数据结构:AVL树的分析与实现
✨✨ 欢迎大家来到贝蒂大讲堂✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:数据结构与算法
贝蒂的主页:Betty’s blog
1. AVL树的介绍
在前面我们学习二叉搜索树时知道,在数据有序或接近有序时二叉搜索树会退化为单边树,查找时相当于在单链表中查找,效率低下。
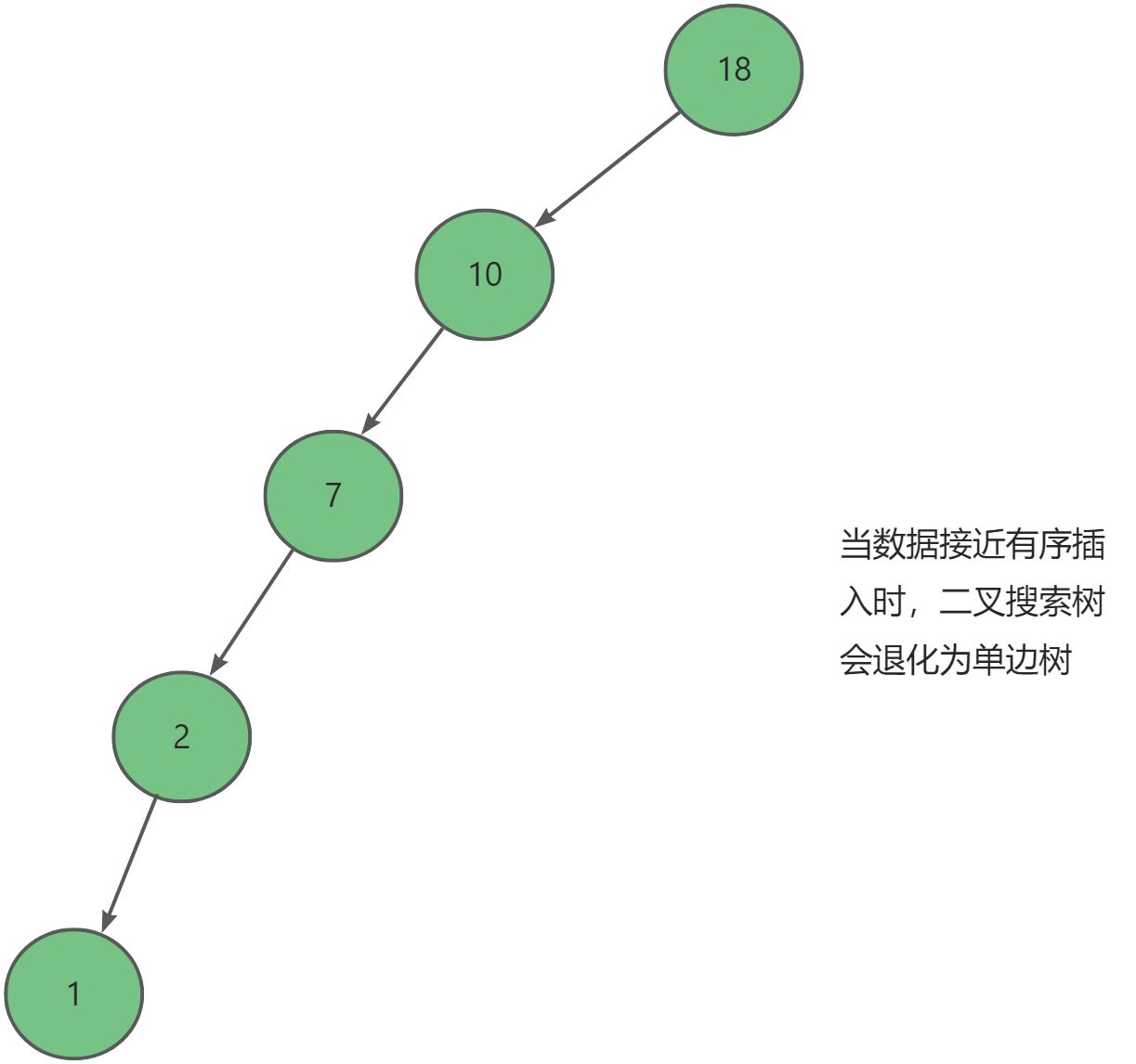
为了解决这个问题,1962 年,两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis提出了一种新方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。而这颗新的树我们平衡二叉搜索(排序)树,简称AVL树。其具有以下特点:
AVL树本质就是一颗二叉搜索树。AVL树左右两棵子树的高度差的绝对值(平衡因子)不超过1。AVL树的左右两棵子树也是一颗AVL树。
其中特别注意:空树也是一颗AVL树,并且由于AVL树也是二叉搜索树,所以AVL树的中序遍历是有序的。
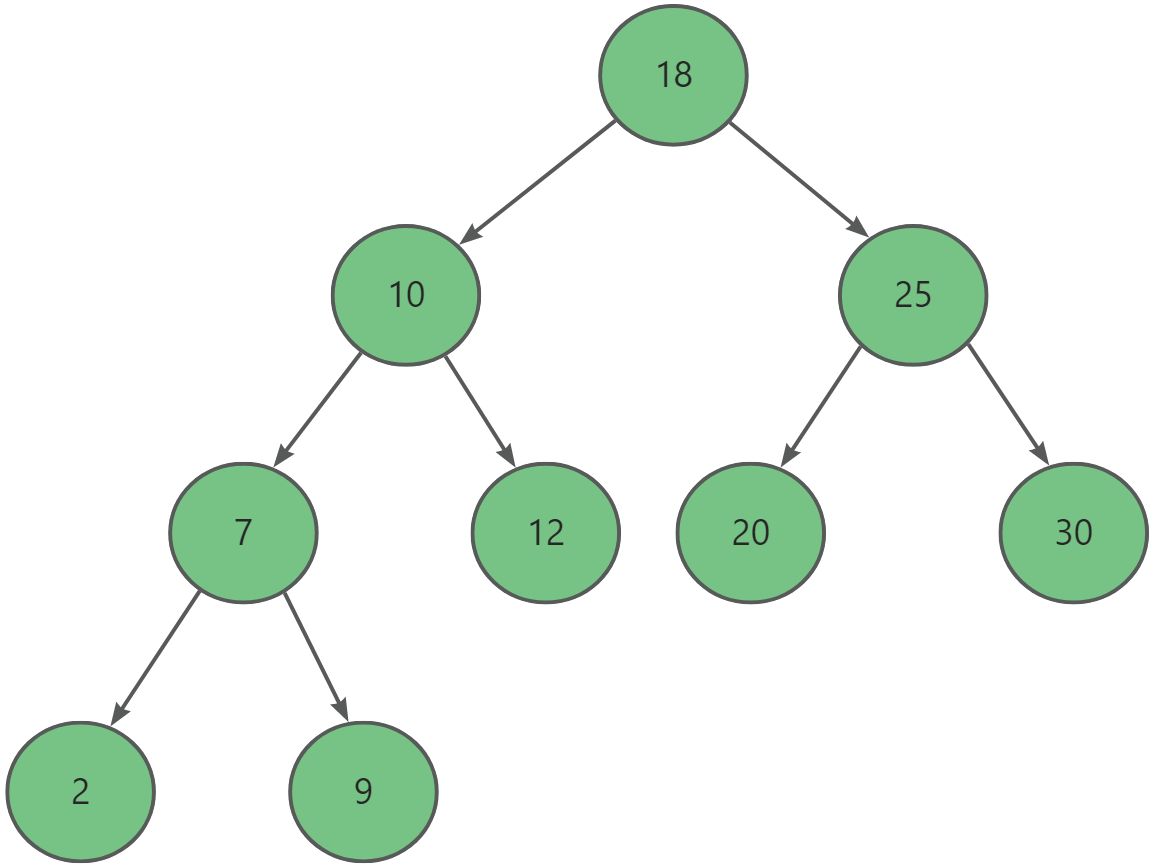
AVL树通过特殊的构造有效的避免了二叉搜索树在数据有序或接近有序时退化为单边树的情况。这使得AVL树在查找、插入和删除操作上,能够保持较为稳定的时间复杂度,而不会因为数据的特殊分布导致性能急剧下降。
2. AVL树的功能
以下是常见的AVL树的功能:
AVL树的插入。AVL树的查找。AVL树的删除。
3. AVL树的结构
3.1. AVL树的节点
AVL树的节点本质与二叉搜索树的节点差不多,所以肯定有三个成员变量:左子树_left,右子树_right,键值_val,并且键值我们采用KV模型的形式。而为了后续调整我们还需一个平衡因子_bf(默认为右子树的高度-左子树的高度)以及一个父节点_parent。当然为了适配不同的类型,我们可以定义一个模版.。
template<class K,class V>
struct AVLTreeNode
{AVLTreeNode(const pair<K, V>& val = pair<K, V>()):_kv(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}pair<K, V> _kv;//kv模型int _bf;//平衡因子AVLTreeNode* _left;//左子树AVLTreeNode* _right;//右子树AVLTreeNode* _parent;//指向父节点
};
3.2. AVL树
然后我们就可以通过节点来定义AVL树,并将根节点初始化为空。
template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://...具体功能
private:Node* _root = nullptr;//根节点
};
4. AVL树的初始化与销毁
4.1. 构造函数/拷贝构造/赋值重载
首先我们直接定义一个无参的构造函数,因为我们在定义拷贝构造之后编译器就不会在生成默认的构造函数了。
AVLTree()
{}
之后我们可以利用递归来实现一个拷贝构造函数。
AVLTree(const AVLTree& t)
{_root = copy(t._root);
}
Node* copy(Node* root)
{// 如果传入的根节点为空,直接返回空指针,表示拷贝结束if (root == nullptr)return nullptr;// 为新树创建一个与原始根节点值相同的新节点Node* newnode = new Node(root->_kv);// 递归地拷贝原始根节点的左子树,并将结果赋给新节点的左指针newnode->_left = copy(root->_left);// 递归地拷贝原始根节点的右子树,并将结果赋给新节点的右指针newnode->_right = copy(root->_right);// 新节点的父节点默认为空newnode->_parent = nullptr;// 如果新节点的左子节点存在,设置其父节点为新节点if (newnode->_left){newnode->_left->_parent = newnode;}// 如果新节点的右子节点存在,设置其父节点为新节点if (newnode->_right){newnode->_right->_parent = newnode;}// 返回新树的根节点指针return newnode;
}
最后我们通过一个简单的方式实现赋值重载——通过形参调用拷贝构造出一个临时变量,然后交换this所指向的变量,这样原本this所指向的对象出了作用域就会销毁,间接实现了实现赋值重载。
AVLTree<K,V>& operator=(const AVLTree <K,V> t)
{//赋值重载this->swap(_root, t._root);return *this;
}
4.2. 析构函数
析构函数需要借助递归释放所有节点,而为了方便我们传参我们可以定义子函数来帮助我们解决。
~AVLTree()
{Destroy(_root);
}
void Destroy(Node*& root)
{if (root == nullptr){return;}//递归销毁左子树Destroy(root->_left);//递归销毁右子树Destroy(root->_right);//销毁根节点delete root;root = nullptr;
}
5. AVL树的功能实现
5.1. AVL树的旋转
我们知道AVL树左右子树的高度差绝对值要保证不超过1,也就是说AVL树的平衡因子_bf只能取-1,0,1三个值。而无论插入还是删除都可能破坏原有的结构,导致AVL树失衡。为了重新平衡AVL树,我们需要重新对其调整。
首先我们可以将AVL树被破坏的情形可以抽象成以下四种场景,其中红色字体代表该节点的平衡因子,蓝色节点代表破坏AVL树平衡的节点。
5.1.1. 右单旋
首先第一种情况就是破坏AVL树平衡的节点位于较高左子树的左侧。
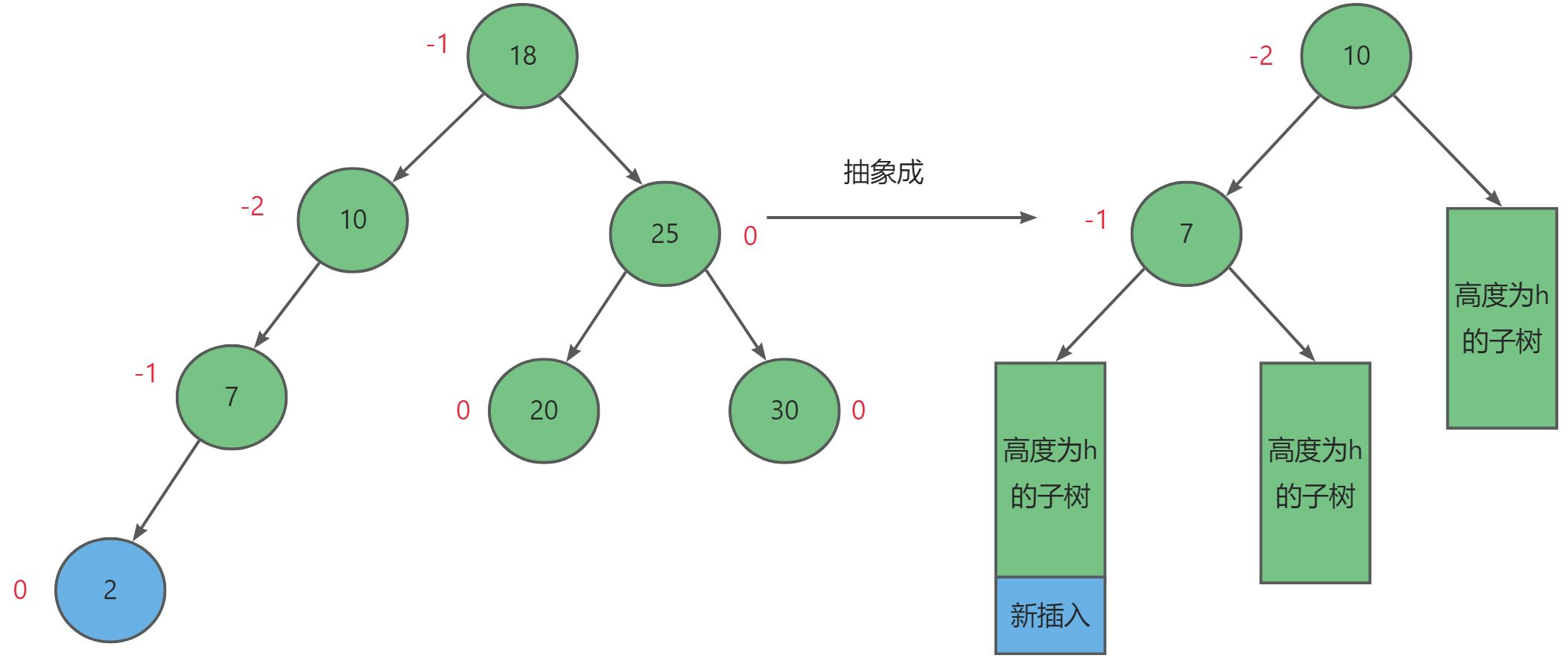
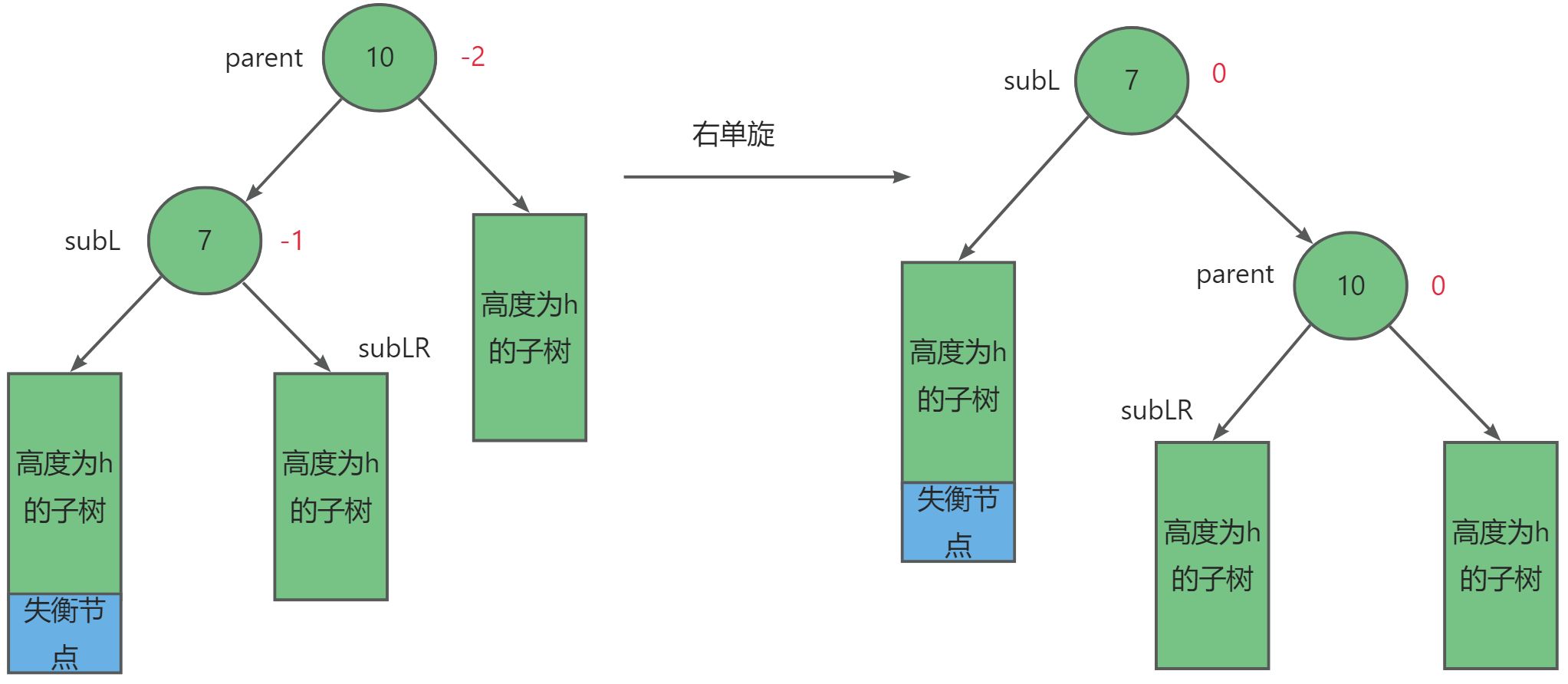
对于这种情况我们需要右单旋的方式,设失衡节点为_parent,其左子树节点为subL,而左子树的右子树为subLR。其调整规则如下:
- 将
subLR链接到parent的左边。- 将
parent链接到subL的右边。- 将
parent与subL的平衡因子置为0。
void RotateR(Node*&parent)
{// 获取父节点的左子节点Node* subL = parent->_left;// 获取父节点左子节点的右子节点Node* subLR = subL->_right;// 1.将subLR链接到parent的左边。parent->_left = subLR;// 如果父节点左子节点的右子节点存在,设置其父节点为当前父节点if (subLR){subLR->_parent = parent;}// 获取父节点的父节点Node* ppNode = parent->_parent;// 2.将parent链接到subL的右边。subL->_right = parent;//parent的父节点指向subLparent->_parent = subL;// 如果父节点存在父节点if (ppNode){// 如果父节点是其父亲节点的左子节点if (ppNode->_left == parent){// 将父节点的父亲节点的左子节点设置为当前父节点的左子节点ppNode->_left = subL;}// 如果父节点是其父亲节点的右子节点else{// 将父节点的父亲节点的右子节点设置为当前父节点的左子节点ppNode->_right = subL;}// 设置父节点左子节点的父节点为父节点的父节点subL->_parent = ppNode;}// 如果父节点为根节点else{// 将根节点设置为父节点的左子节点_root = subL;// 将父节点左子节点的父节点设置为空subL->_parent = nullptr;}//3.将parent与subL的平衡因子置为0。subL->_bf = parent->_bf = 0;//改变parent节点的指向,方便erase中的node返回parent = subL;
}
其中需要特别注意的就是:判断父节点**_parent**到底是根节点,还是某个节点的子节点。
5.1.2. 左单旋
第二种情况就是破坏AVL树平衡的节点位于较高右子树的右侧。
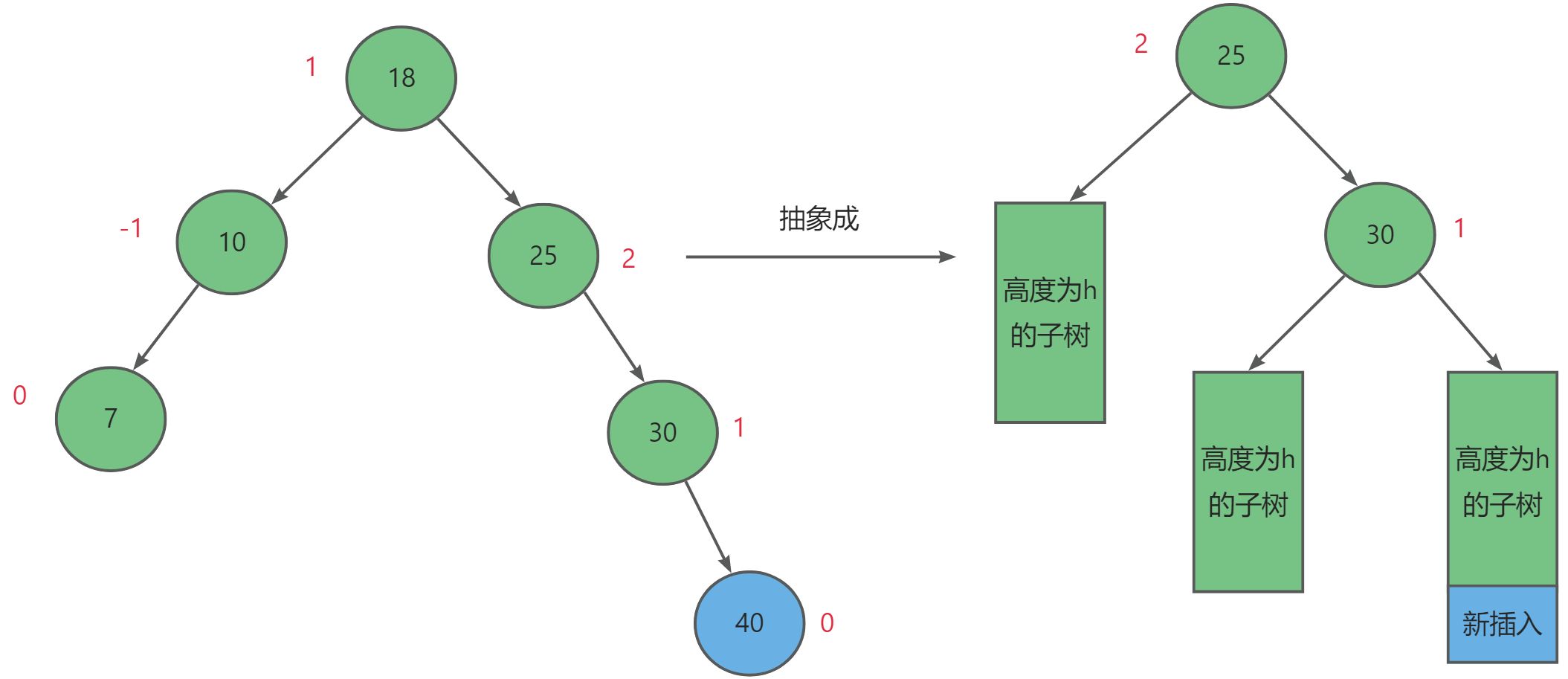
对于这种情况我们需要左单旋的方式,设失衡节点为_parent,其右子树节点为subR,而有右子树的左子树为subRL。其调整规则如下:
- 将
subRL链接到parent的右边。- 将
parent链接到subR的左边。- 将
parent与subR的平衡因子置为0。
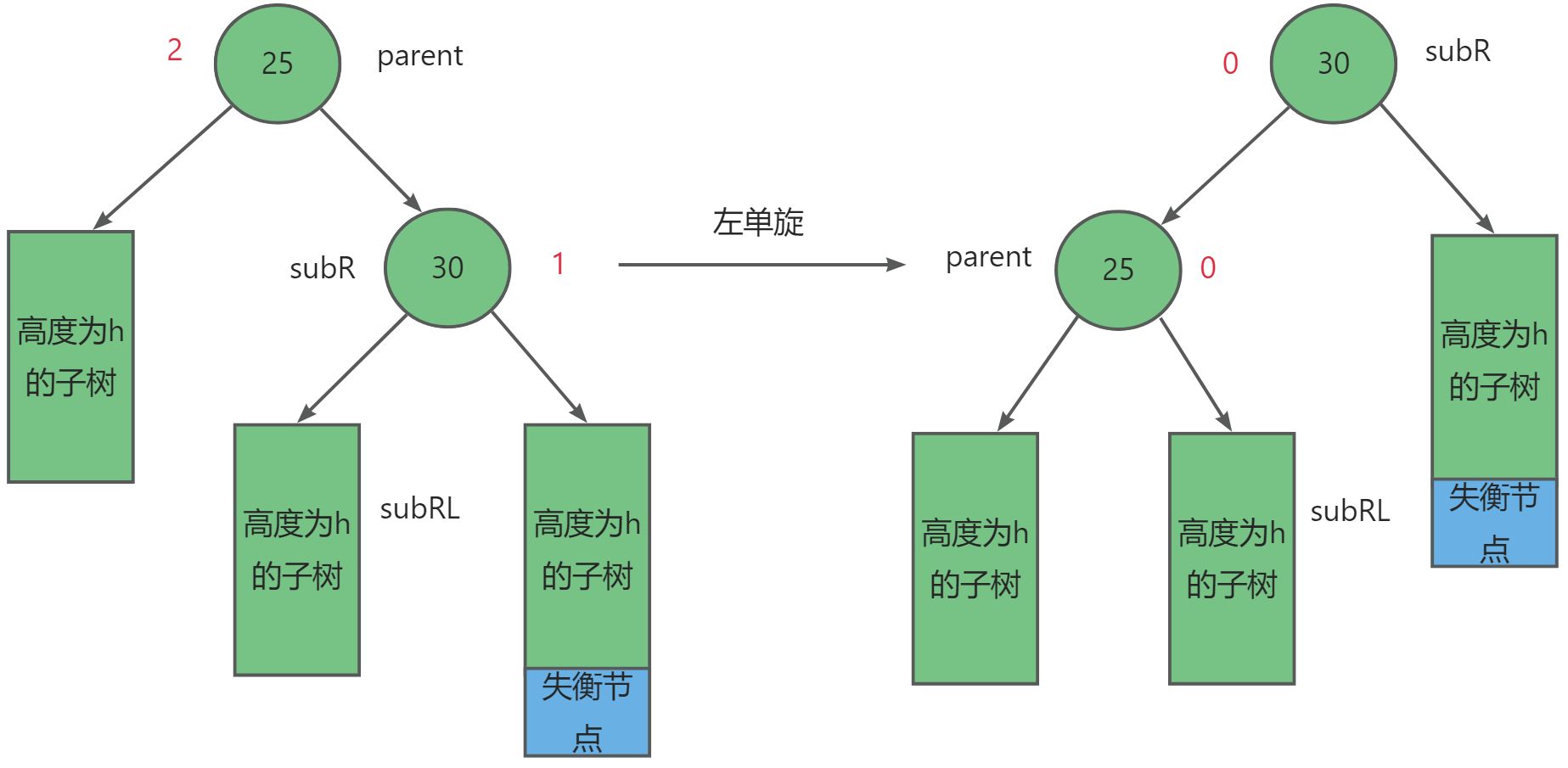
void RotateL(Node* &parent)
{// 获取父节点的右子节点Node* subR = parent->_right;// 获取父节点右子节点的左子节点Node* subRL = subR->_left;//1.将subRL链接到parent的右边。parent->_right = subRL;// 如果父节点右子节点的左子节点存在,设置其父节点为当前父节点if (subRL){subRL->_parent = parent;}// 获取父节点的父节点Node* ppNode = parent->_parent;//2.将parent链接到subR的左边。subR->_left = parent;// 设置父节点的父节点为右子节点parent->_parent = subR;// 如果父节点存在父节点if (ppNode){// 如果父节点是其父亲节点的左子节点if (ppNode->_left == parent){// 将父节点的父亲节点的左子节点设置为当前父节点的右子节点ppNode->_left = subR;}// 如果父节点是其父亲节点的右子节点else{// 将父节点的父亲节点的右子节点设置为当前父节点的右子节点ppNode->_right = subR;}// 设置父节点右子节点的父节点为父节点的父节点subR->_parent = ppNode;}// 如果父节点为根节点else{// 将根节点设置为父节点的右子节点_root = subR;// 将父节点右子节点的父节点设置为空subR->_parent = nullptr;}// 3.将parent与subR的平衡因子置为0。subR->_bf = parent->_bf = 0;//改变parent节点的指向,方便erase中的node返回parent = subR;
}
其中需要特别注意的就是:判断父节点**_parent**到底是根节点,还是某个节点的子节点。
5.1.3. 先左单旋,再右单旋
第三种情况就是破坏AVL树平衡的节点位于较高左子树的右侧。
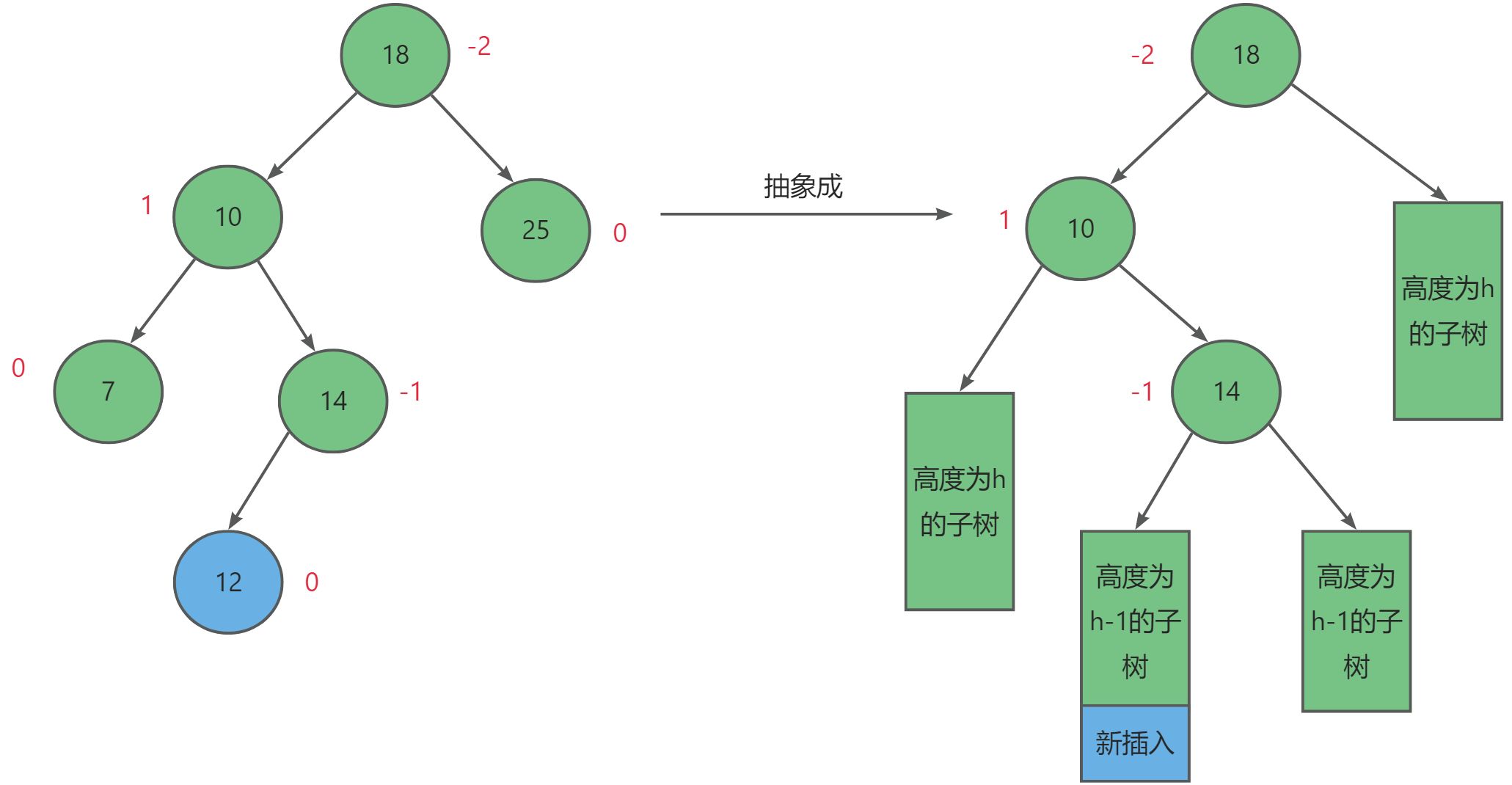
对于这种情况我们需要先左单旋,再右单旋的方式,设失衡节点为_parent,其左子树节点为subL,而有左子树的右子树为subLR。其调整规则如下:
- 先对
subL进行左单旋。- 在对
parent进行右单旋。- 调整平衡因子。
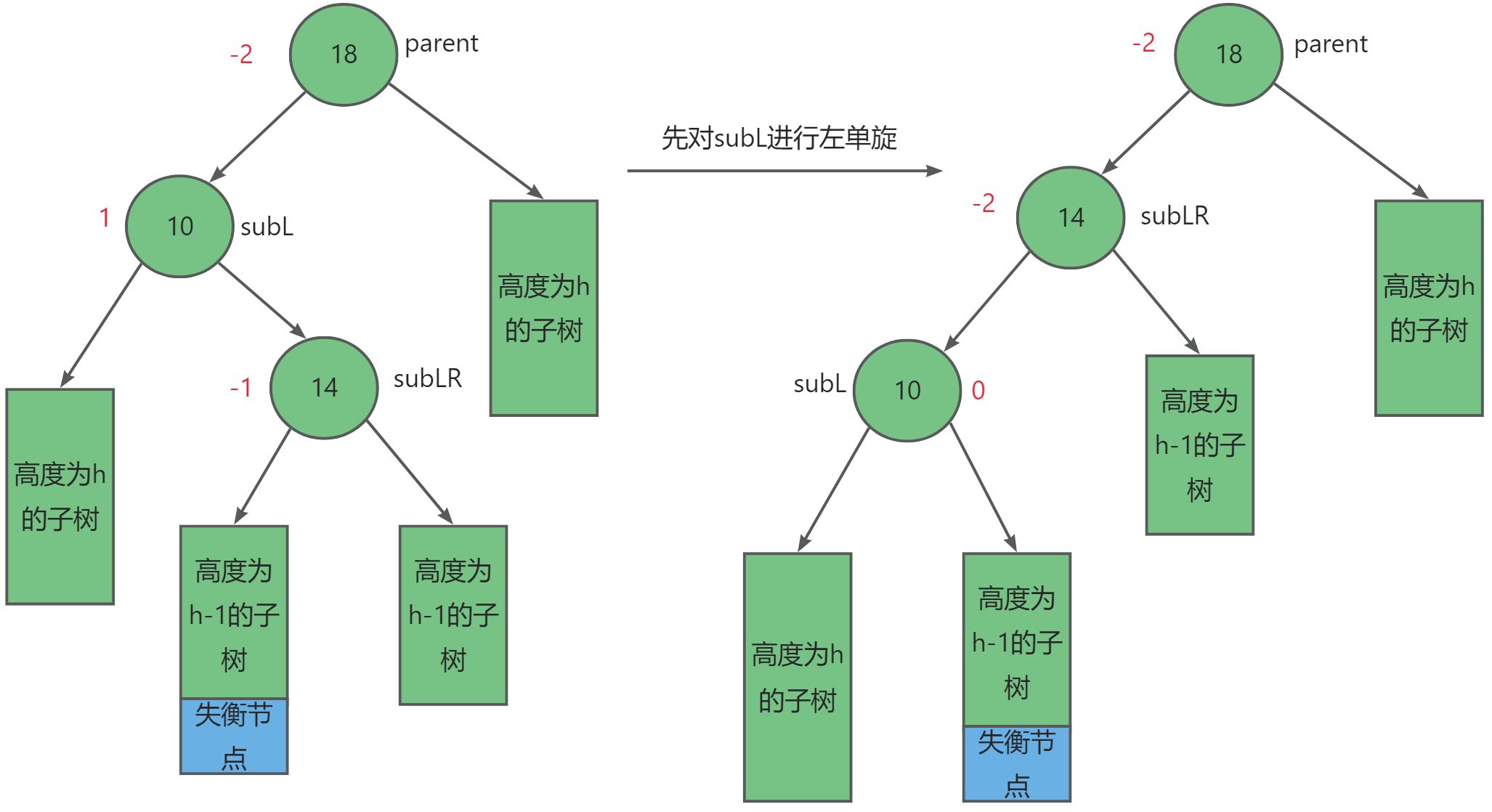
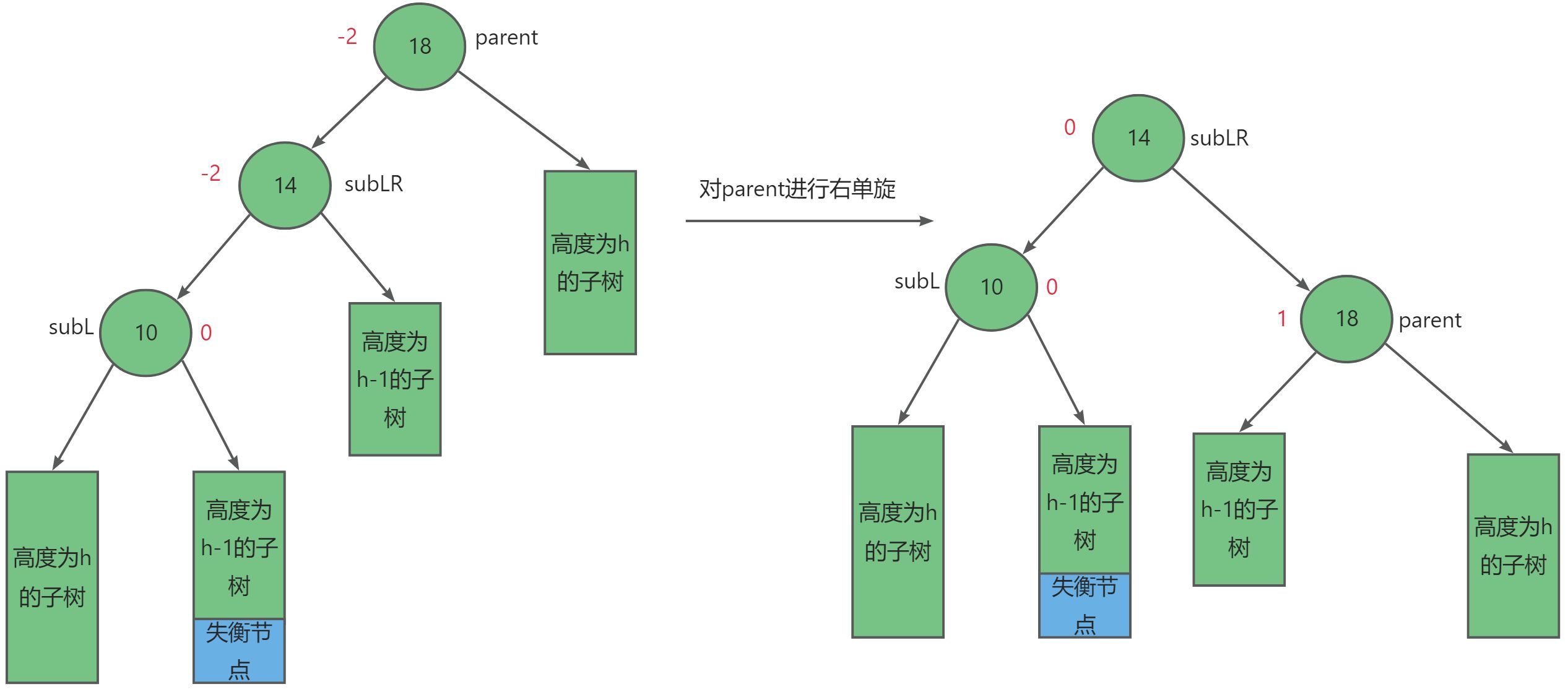
但是平衡因子的调整又可以分别三种情况:
- 当
subLR = -1时,如上图所示,调整后subL = 0,subLR = 0,parent = 1。 - 当
subLR = 0,即h = 0时:
比如依次插入三个节点,10,5,6,如下图所示:
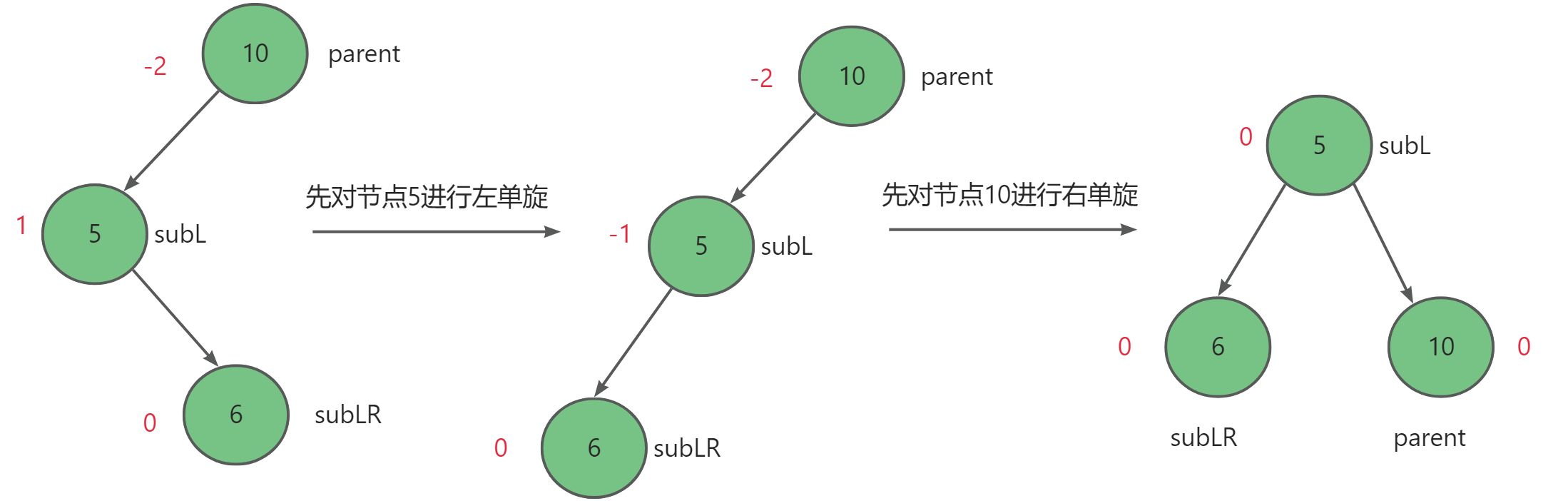
调整后subL = 0,subLR = 0,parent = 0。
- 当
subLR = 1时,具体情况如下图:
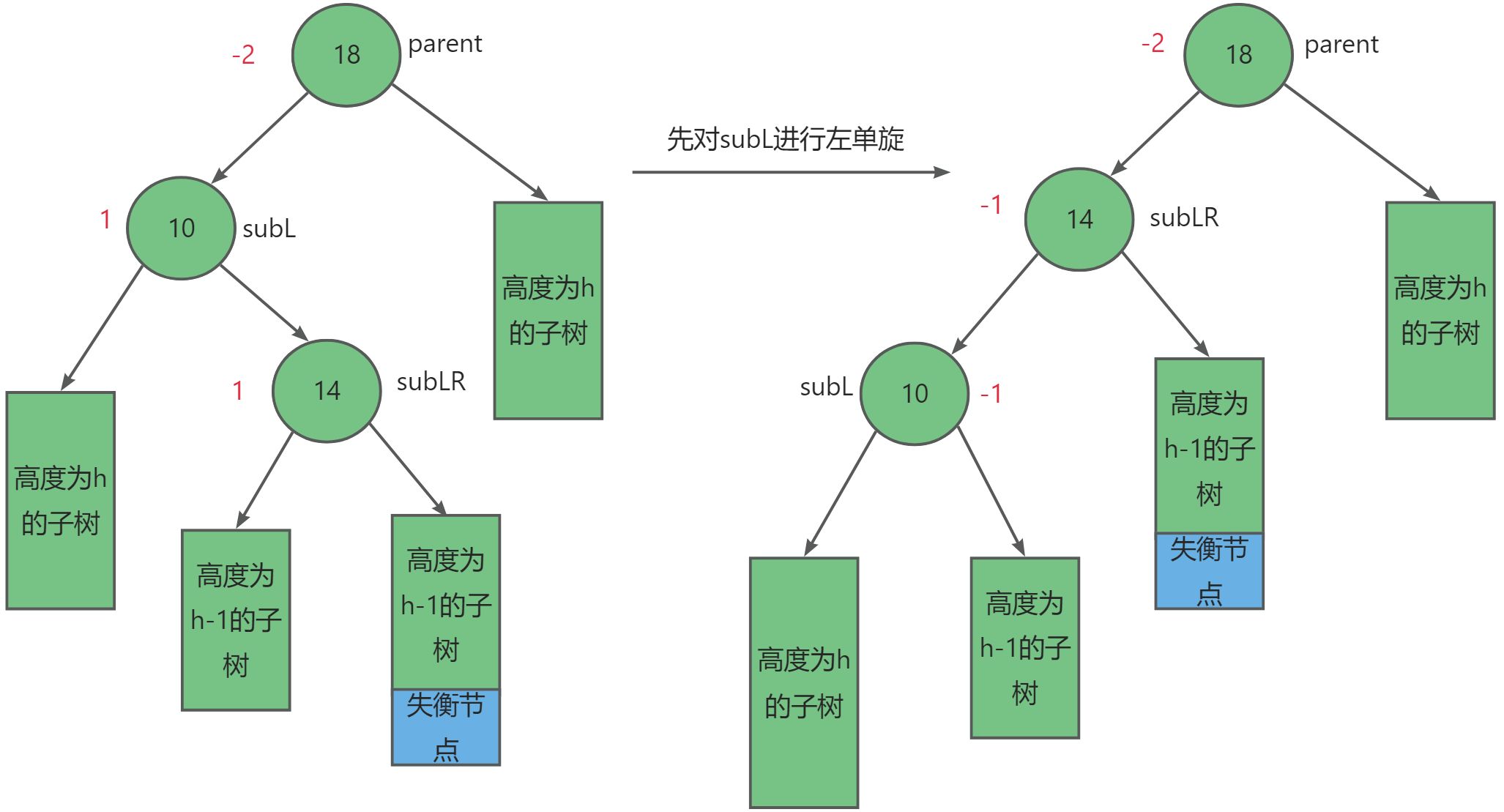
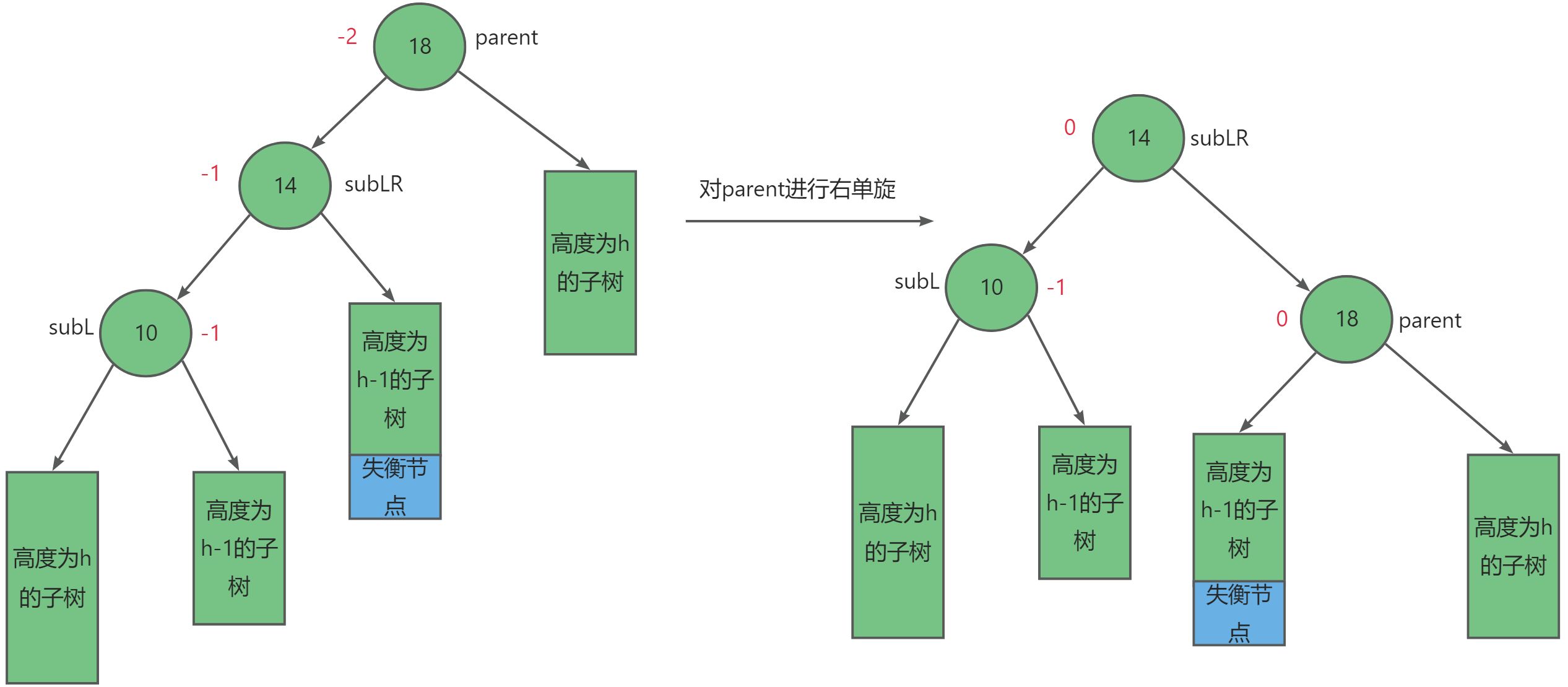
调整后subL = -1,subLR = 0,parent = 0。
最后我们可以总结一下:
- 当
subLR = 0时:调整为subLR = 0,subL = 0,parent = 0。- 当
subLR = -1时:调整为subLR = 0,subL = 0,parent = 1。- 当
subLR = 1时:调整为subLR = 0,subL = -1,parent = 0。
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//先左旋RotateL(parent->_left);//再右旋RotateR(parent);//1.情况1if (bf == 0){parent->_bf = subL->_bf = subLR->_bf = 0;}//2.情况2else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}//3.情况3else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{//走到这里说明AVL树有问题assert(false);}
}
5.1.4. 先右单旋,再左单旋
最后一种情况就是破坏AVL树平衡的节点位于较高右子树的左侧。
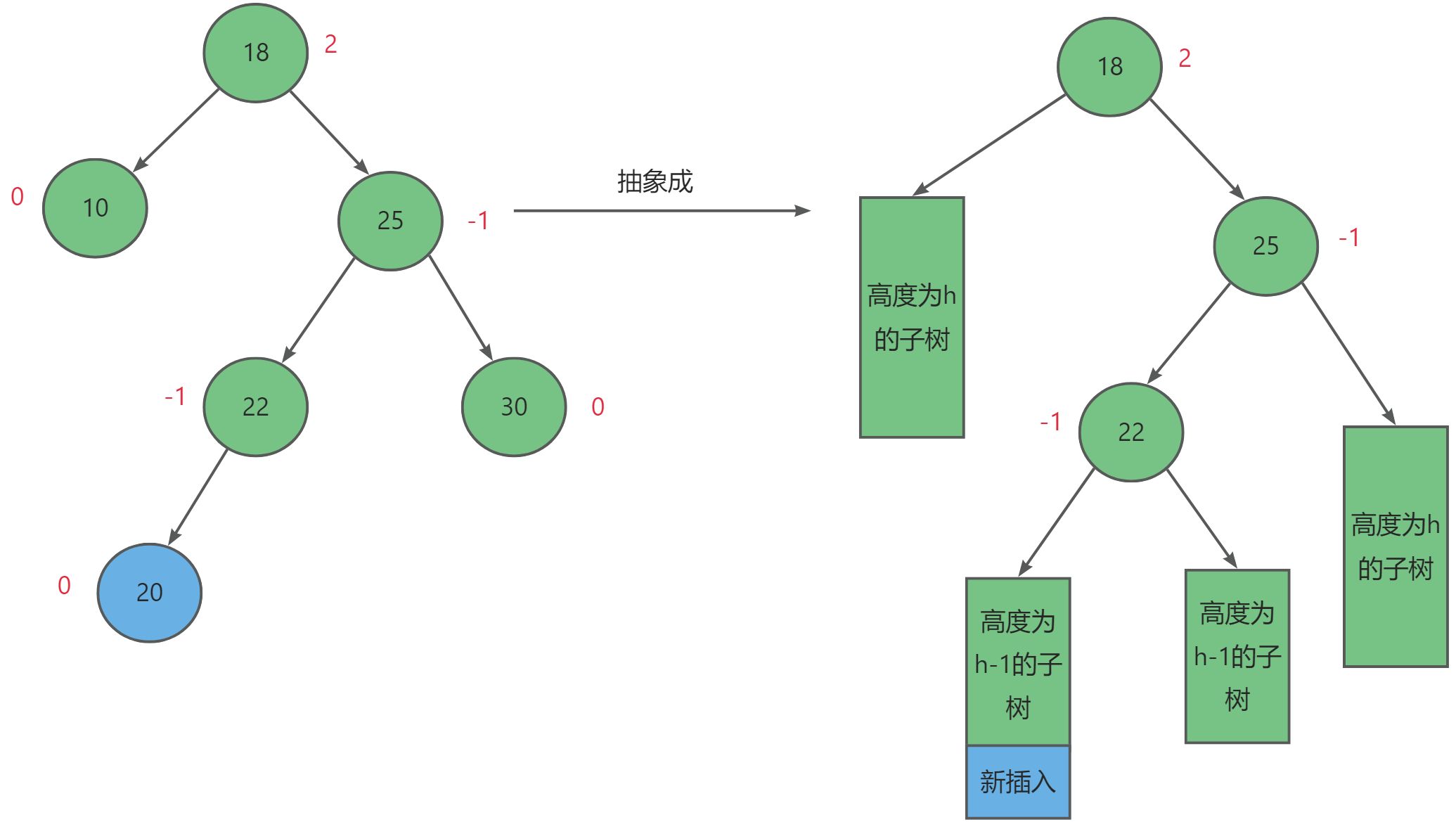
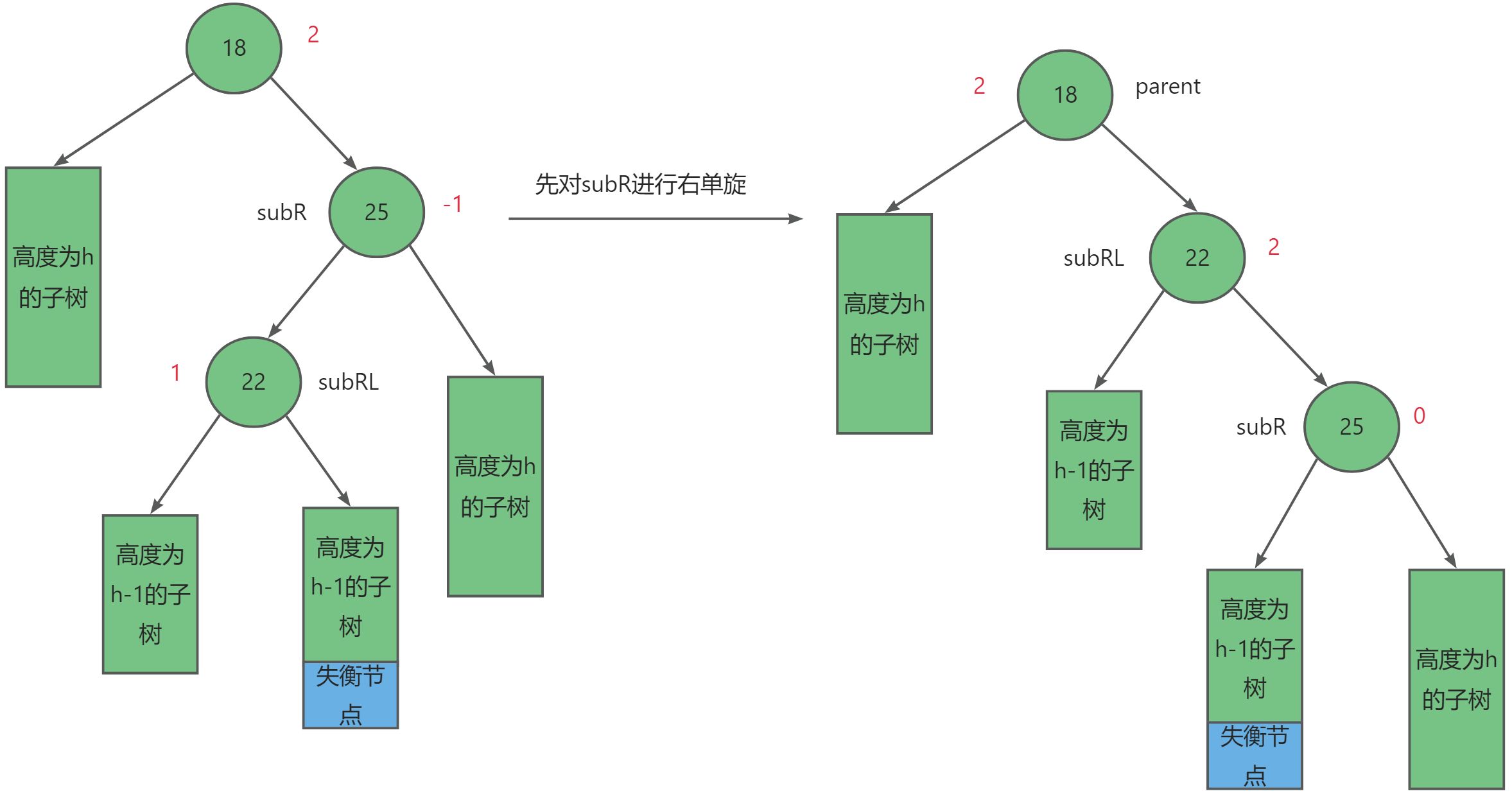
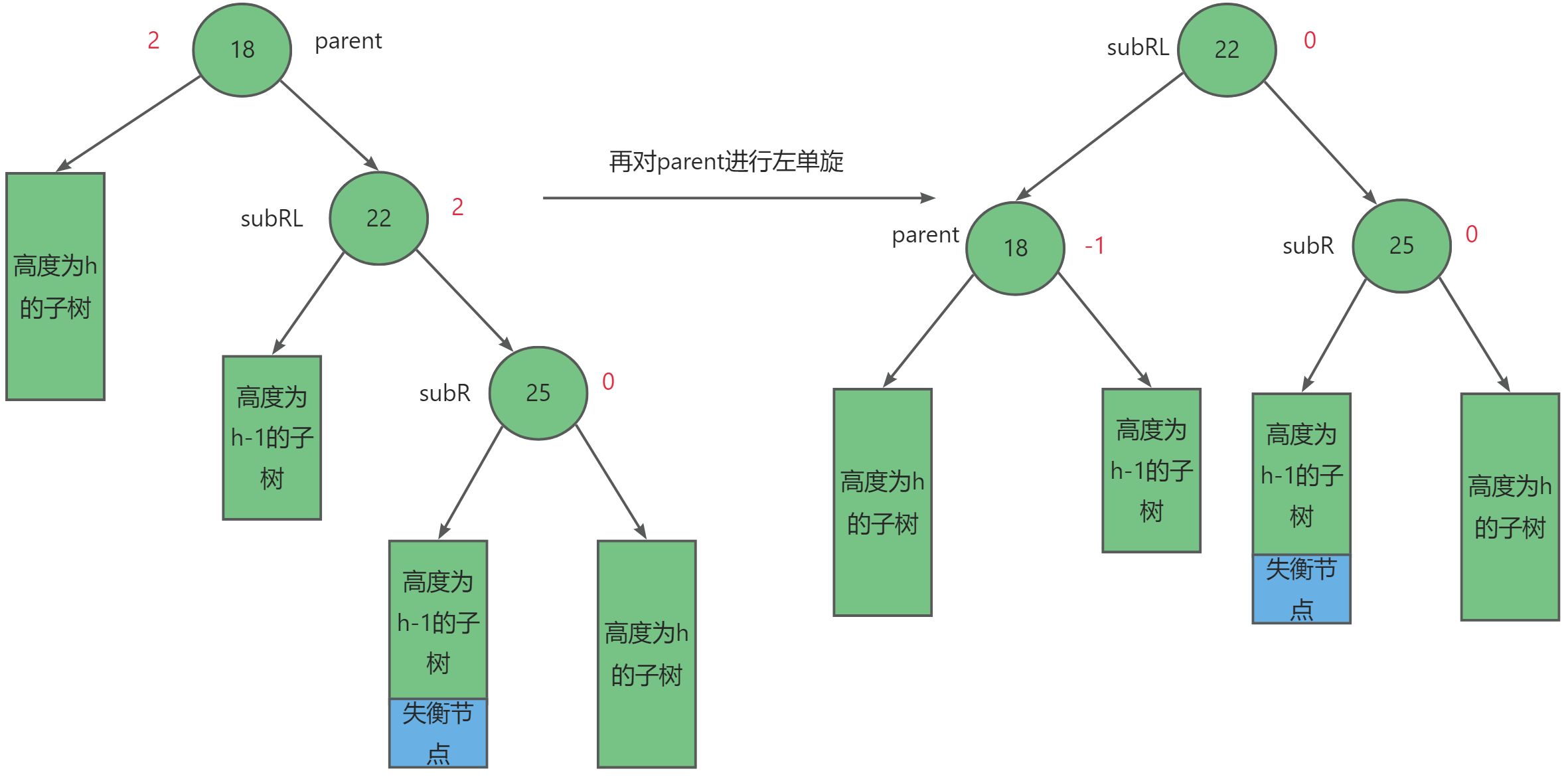
对于这种情况我们需要先右单旋,再左单旋的方式,设失衡节点为_parent,其右子树节点为subR,而有右子树的左子树为subRL。其调整规则如下:
- 先对
subR进行右单旋。- 在对
parent进行左单旋。- 调整平衡因子。
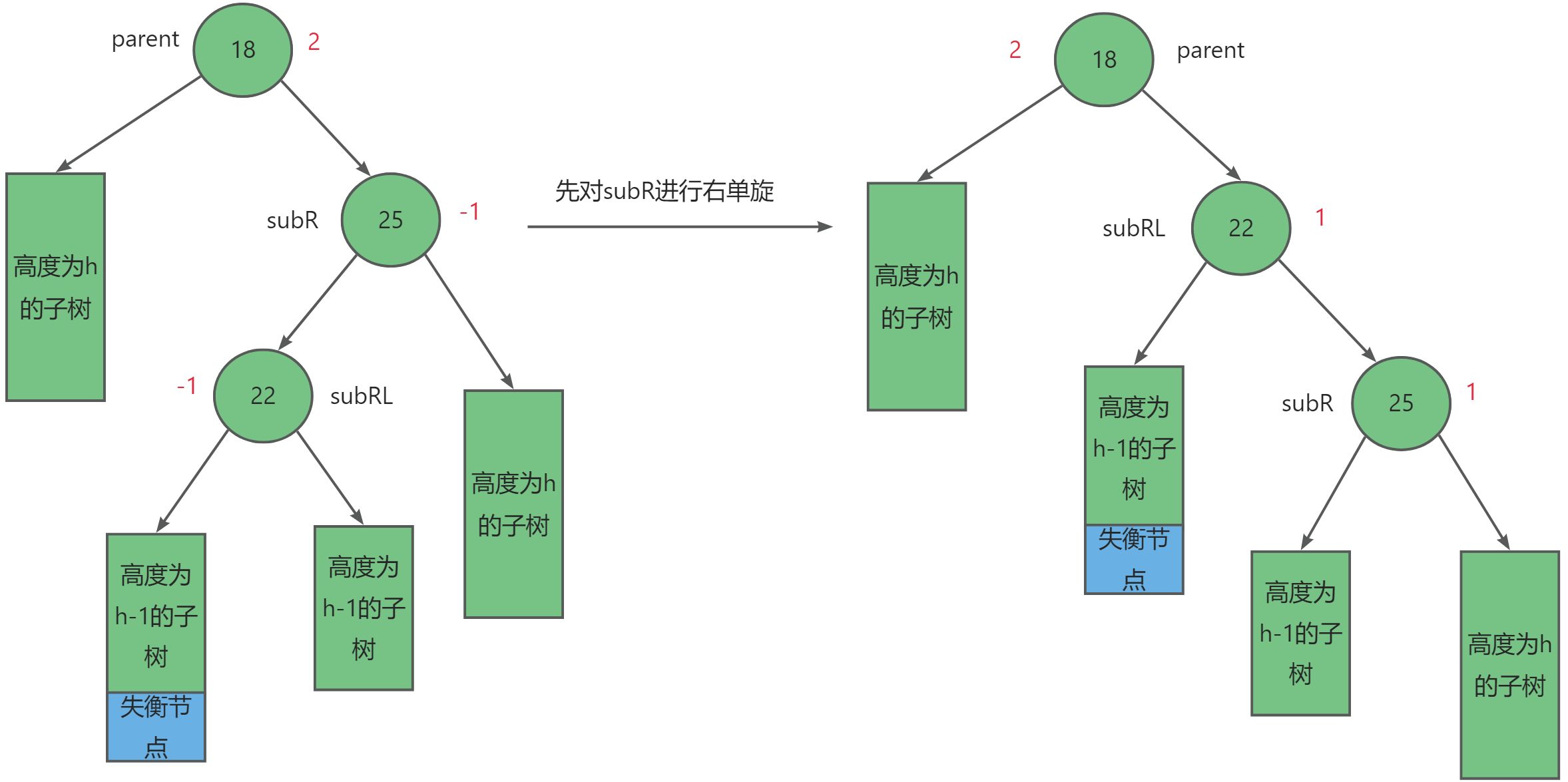
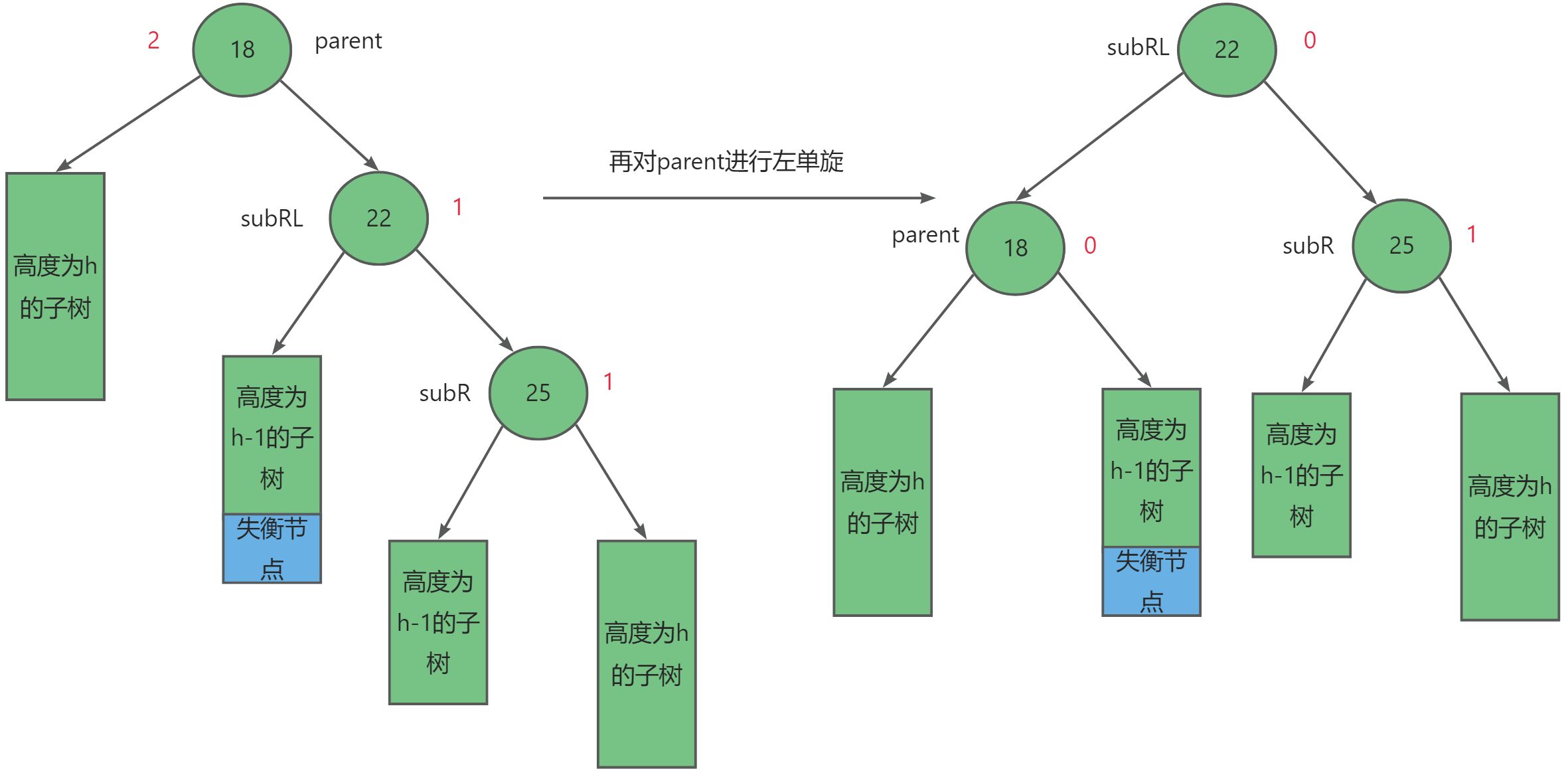
同理,平衡因子的调整又可以分别三种情况:
- 当
subRL = -1时,如上图所示,调整后subR = 1,subRL = 0,parent = 0。 - 当
subRL = 0,即h = 0时:
比如依次插入三个节点,5,10,6,如下图所示:
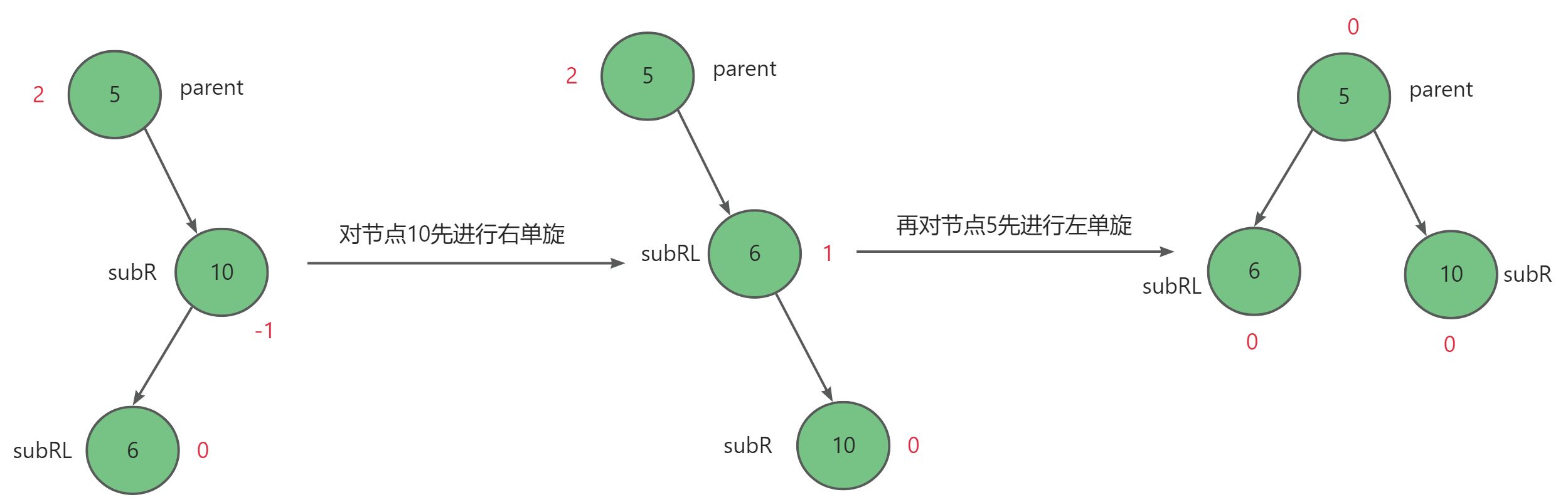
调整后subR = 0,subRL = 0,parent = 0。
3.当subRL = 1时,具体情况如下图:
调整后subR = 0,subRL = 0,parent = -1。
最后我们可以总结一下:
- 当
subRL = 0时:调整为subRL = 0,subR = 0,parent = 0。- 当
subRL = -1时:调整为subRL = 0,subR = 1,parent = 0。- 当
subRL = 1时:调整为subRL = 0,subL = 0,parent = -1。
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//先右单旋Rotate(parent->_right);Rotate(parent);//1.情况一if (bf == 0){parent->_bf = subRL->_bf = subR->_bf = 0;}//2.情况二else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}//3.情况三else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else{//走到这里说明AVL树出错assert(false);}
}
5.2. AVL树的插入
向AVL树进行插入,首先是先找到需要插入的位置,这个逻辑与二叉搜索树类似,这里就不在赘述。找到之后对父节点的平衡因子进行更新,更新平衡因子就可以分为以下三种大的情况:
- 父节点平衡因子为 0,整体高度不变,不需要再向上调整平衡因子。
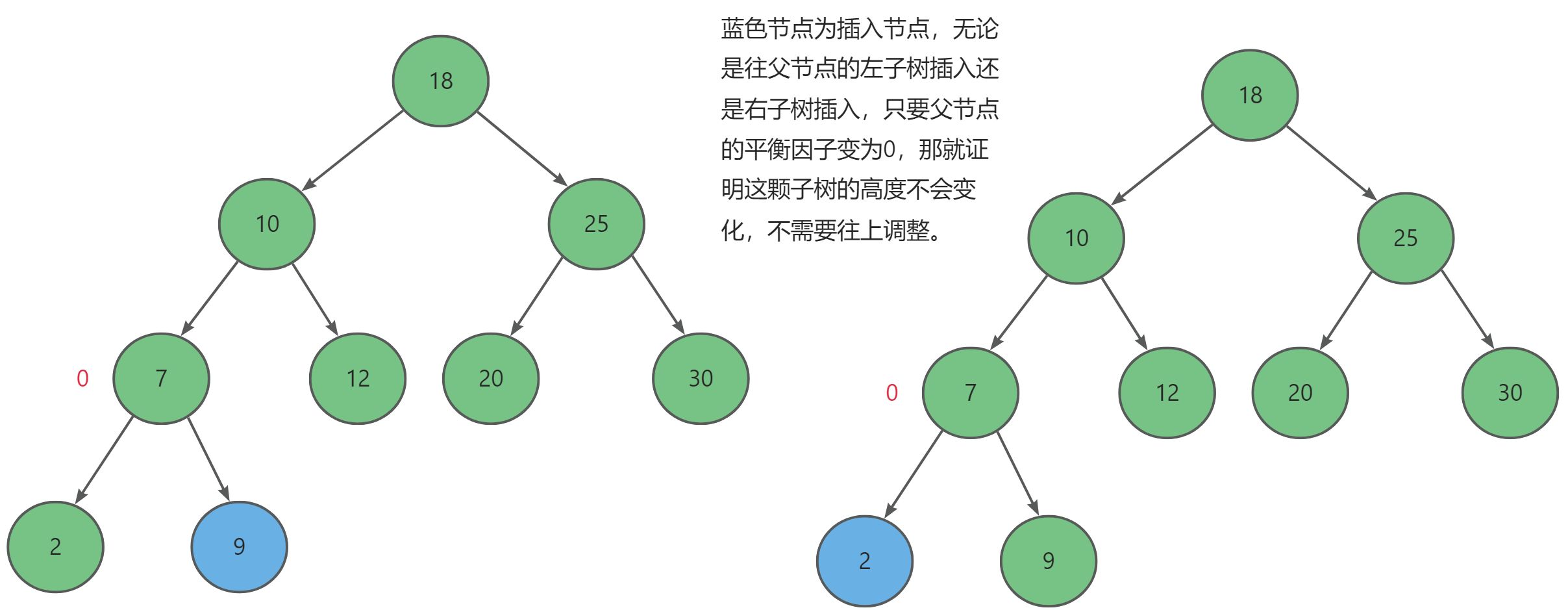
- 父节点平衡因子为1或-1,整体高度改变,需要再向上调整平衡因子。
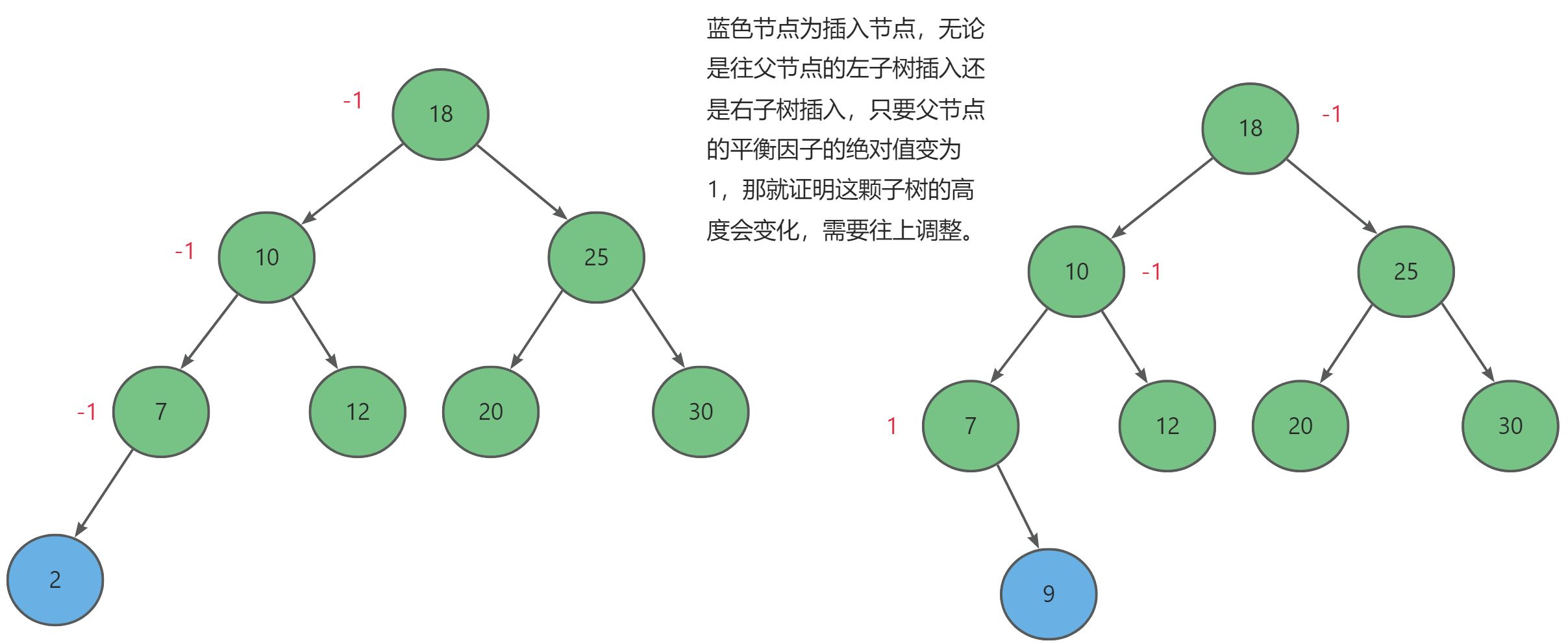
- 父节点平衡因子为2或-2,平衡被破坏,需要进行旋转。
平衡被破坏同样可以分为四种情况,与旋转的方式想对应,其中蓝色为插入节点。首先第一种往较高左子树的左侧插入,此时parent = -2,subL = -1,进行右单旋。
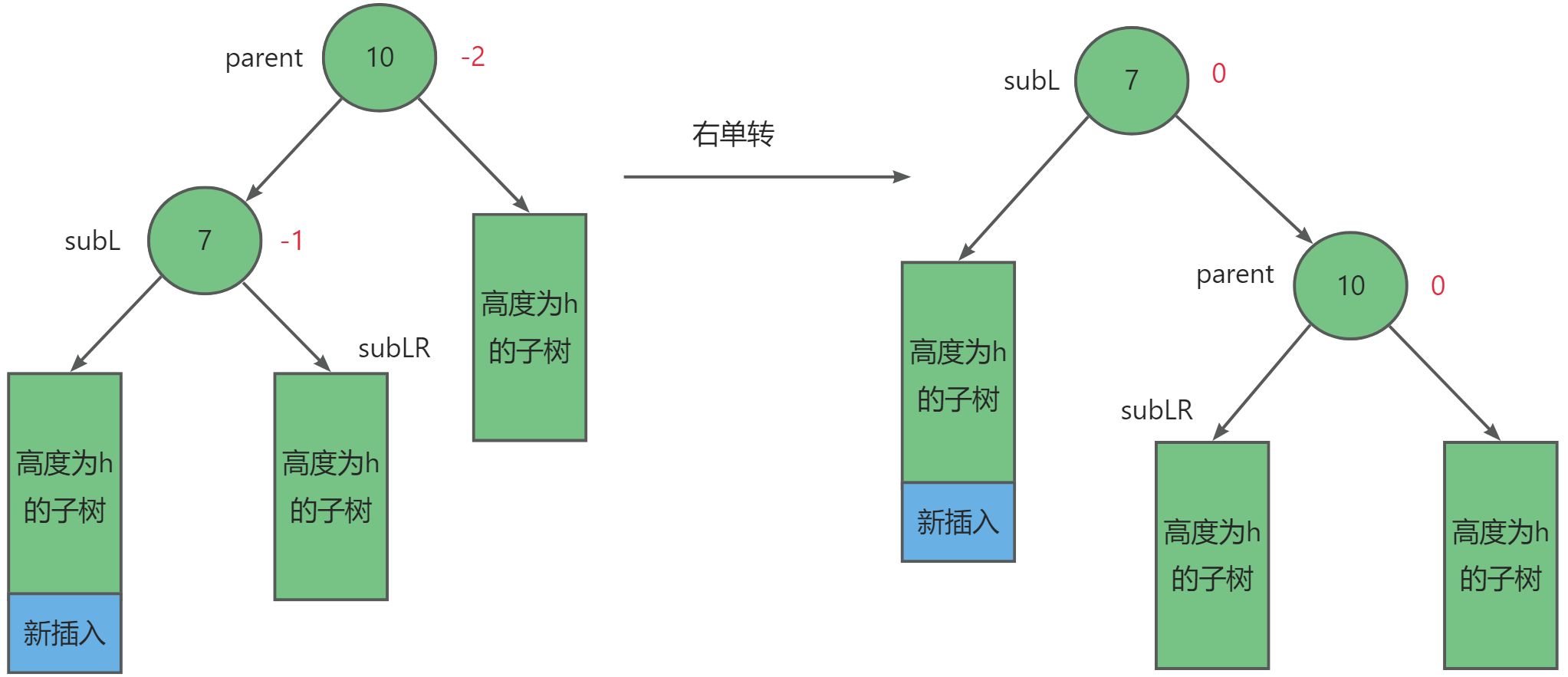
第二种往较高右子树的右侧插入,此时parent = 2,subL = 1,进行左单旋。
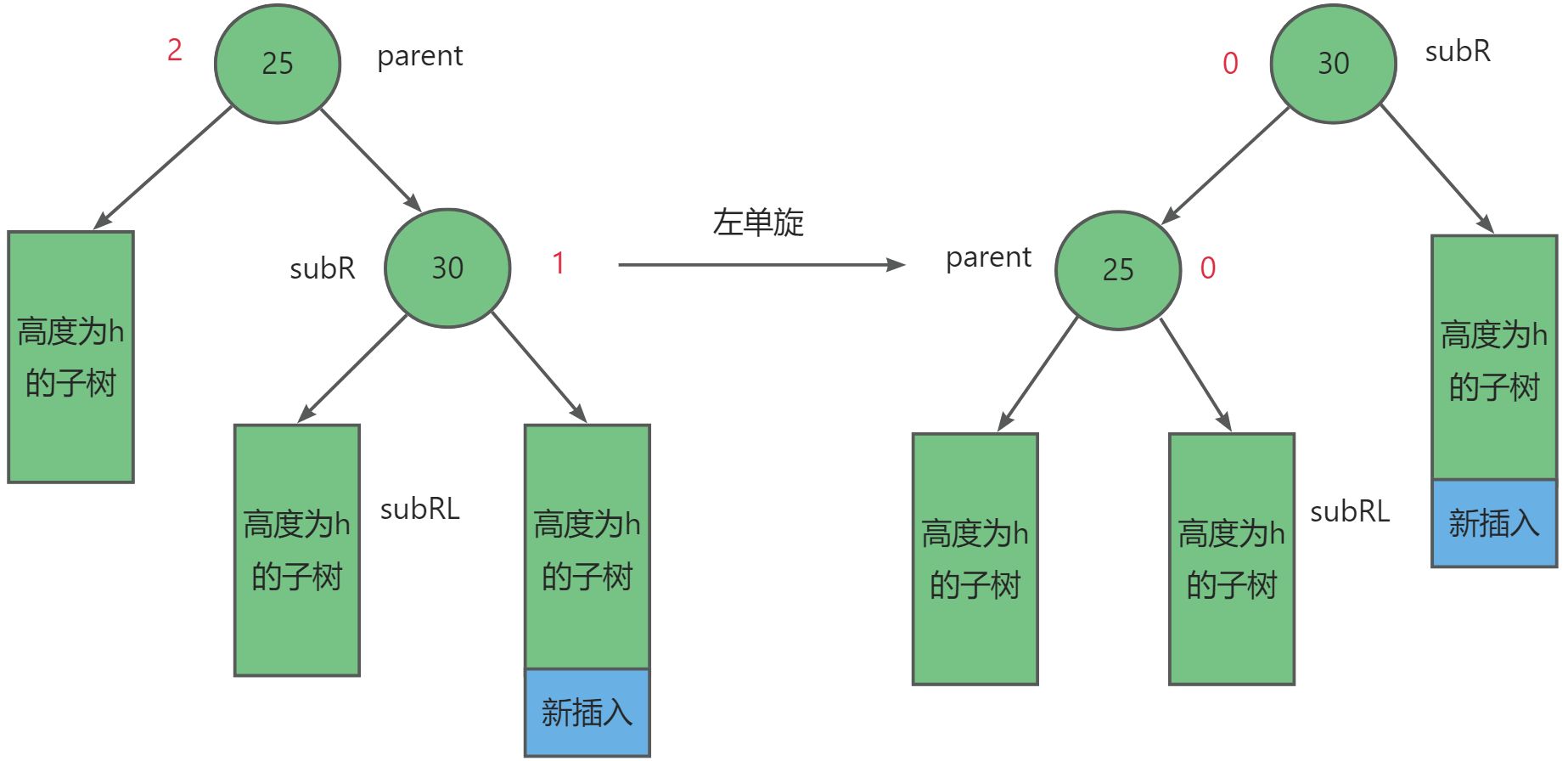
第三种往较高左子树的右侧插入,此时parent = -2,subL = 1,先左旋再右旋。
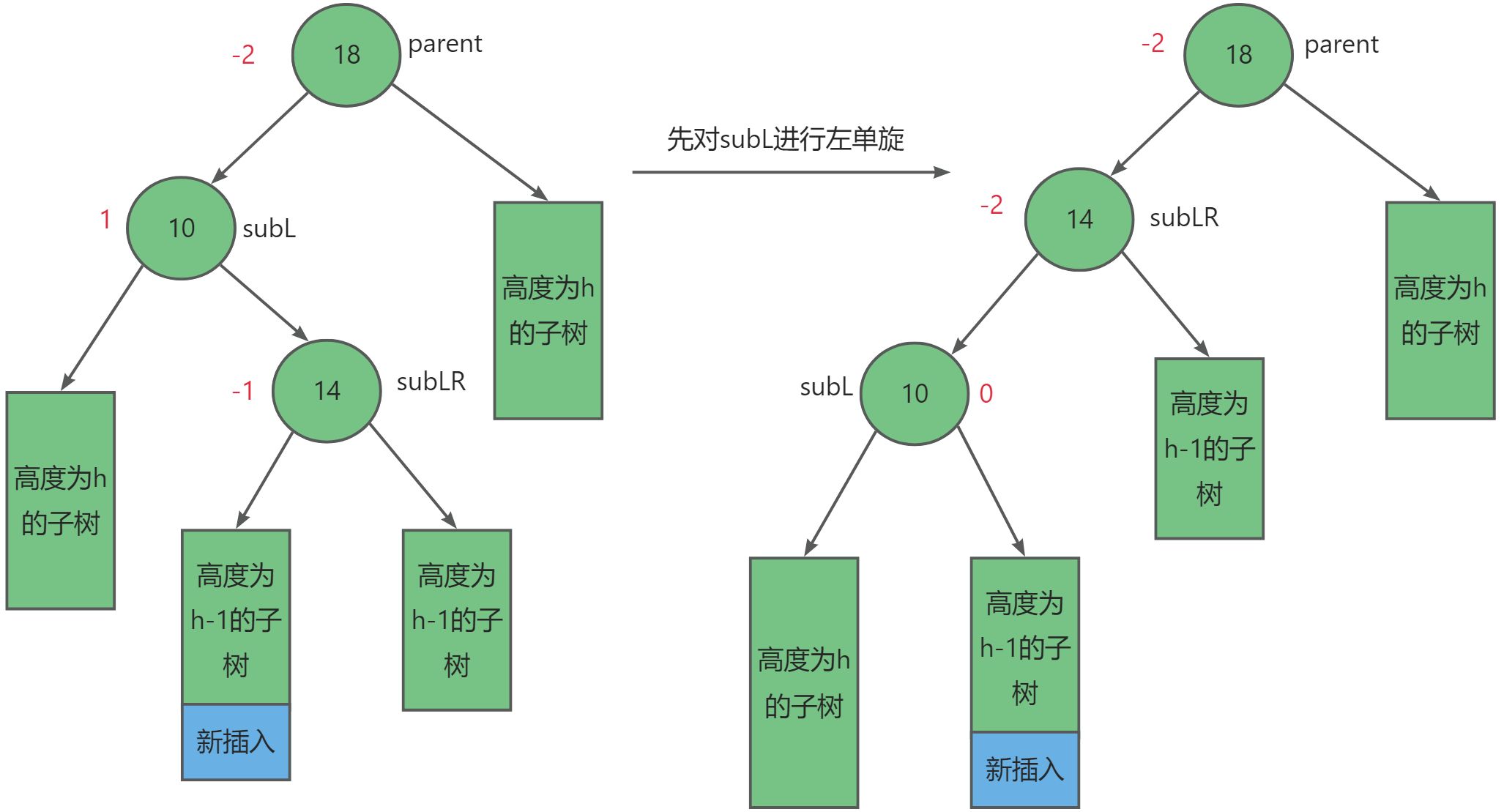
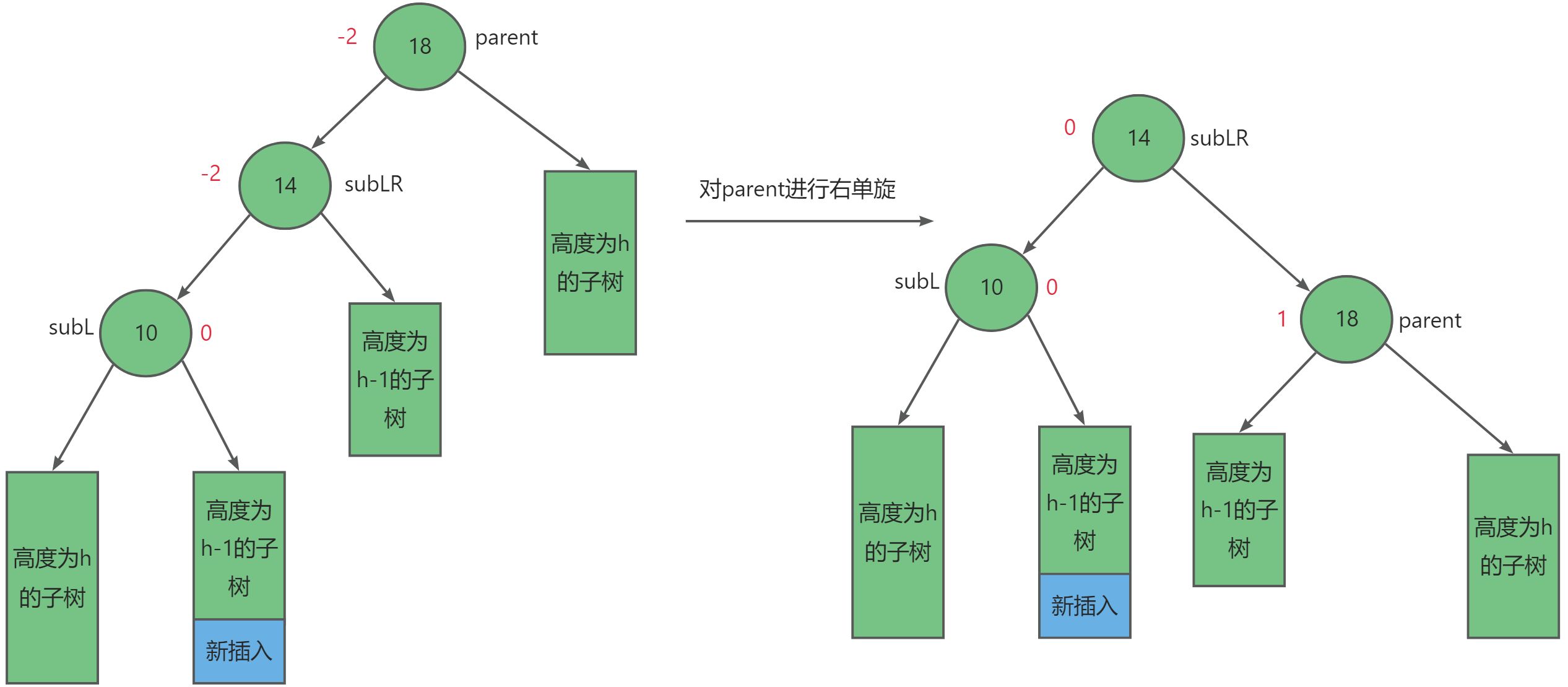
第四种往较高右子树的右侧插入,先右旋再左旋,此时parent = 2,subR = -1,先右旋再左旋。
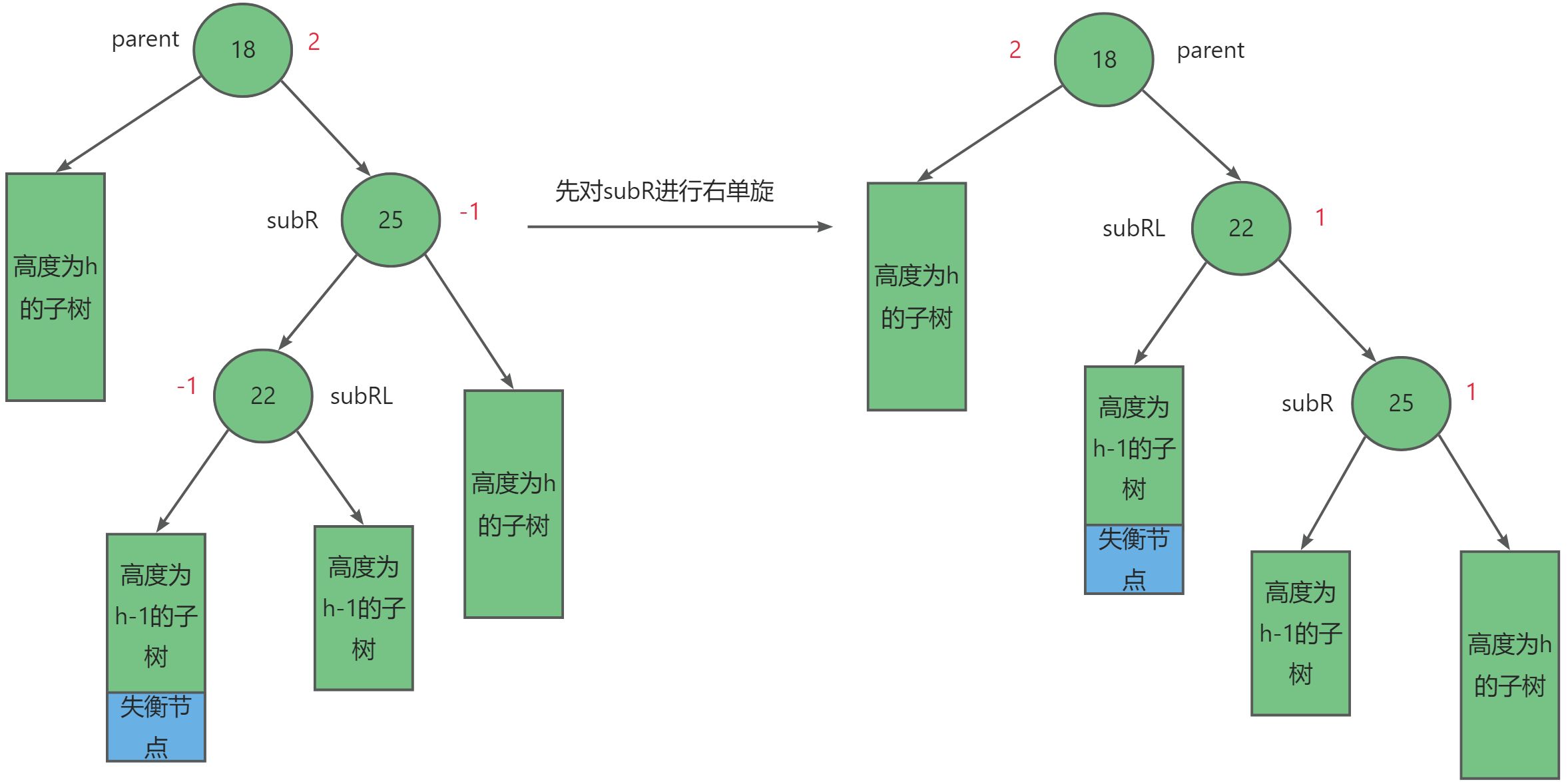
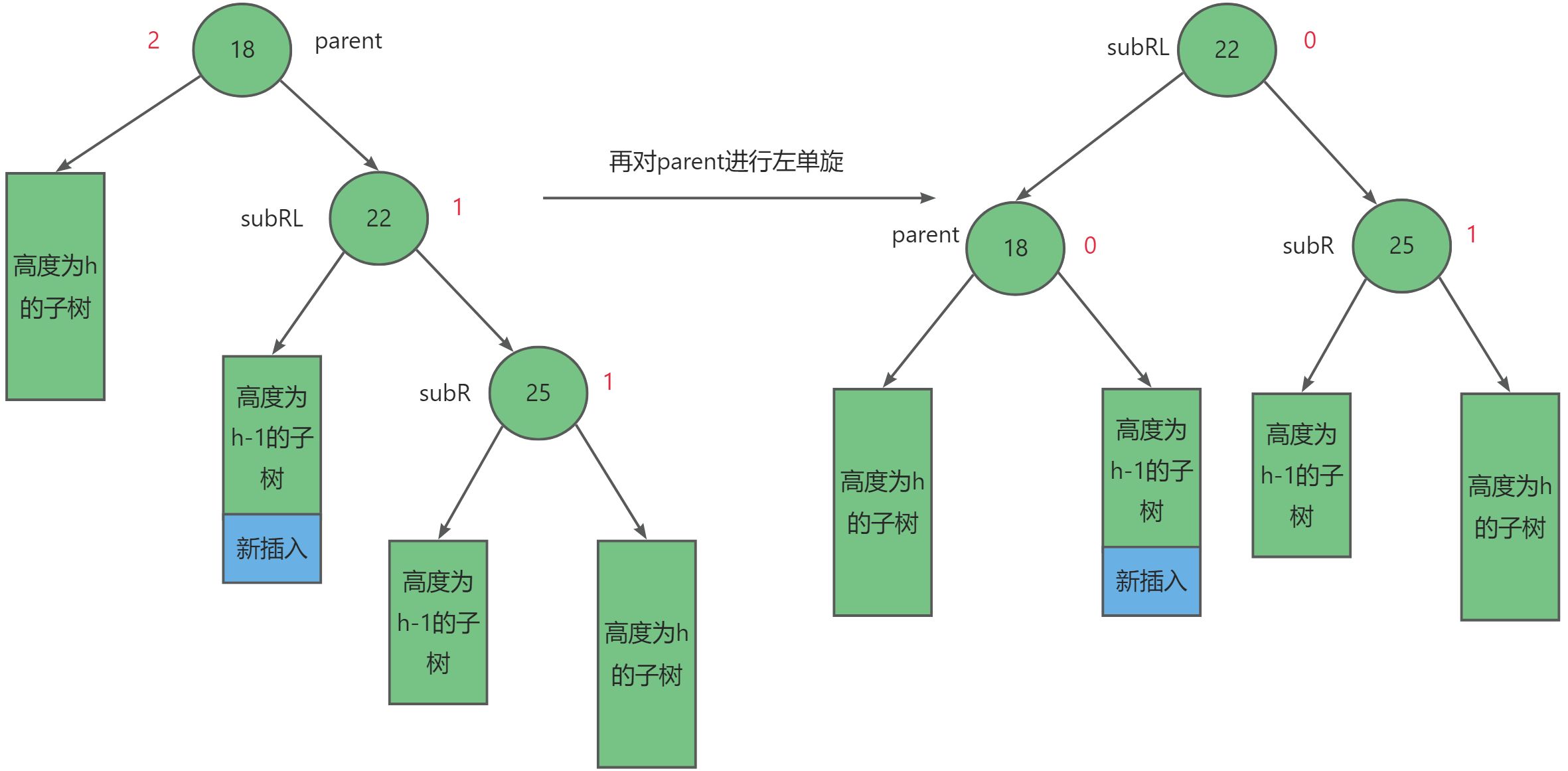
最后我们可以归纳总结出:
- 父节点平衡因子为 0,整体高度不变,不需要再向上调整平衡因子。
- 父节点平衡因子为1或-1,整体高度改变,需要再向上调整平衡因子。
- 父节点平衡因子为2或-2,平衡被破坏,需要进行旋转。设父节点为
parent,插入方向子节点为cur。
parent = -2且cur = -1进行右单旋。parent = 2且cur = 1进行左单旋。parent = -2且cur = 1进行先进行左单旋,再进行右单旋。parent = 2且cur = -1进行先进行右单旋,再进行左单旋。
bool insert(const pair<K, V>& kv){// 如果根节点为空,创建新节点作为根节点并设置平衡因子为 0,然后返回插入成功if (_root == nullptr){_root = new Node(kv);_root->_bf = 0;return true;}// 初始化父节点为空,当前节点为根节点Node* parent = nullptr;Node* cur = _root;// 查找插入位置while (cur){// 小于当前节点,往左子树if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}// 大于当前节点,往右子树else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}// 键已存在,返回插入失败else{return false;}}// 找到插入位置,创建新节点cur = new Node(kv);// 根据键值大小确定新节点在父节点的位置if (kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更新平衡因子while (parent){// 如果插入在左边,父节点的平衡因子减 1if (cur == parent->_left){parent->_bf--;}// 如果插入在右边,父节点的平衡因子加 1else{parent->_bf++;}// 如果父节点平衡因子为 0,整体高度不变,不需要再向上调整if (parent->_bf == 0){break;}// 平衡因子为 1 或 -1,需要继续向上调整else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}// 平衡因子为 -2 或 2,需要进行旋转操作以保持平衡else if (parent->_bf == -2 || parent->_bf == 2){// 右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}// 左单旋else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}// 左右双旋else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}// 右左双旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}// 插入之前 AVL 树就已经不平衡了,断言else{assert(false);}}return true;}
5.3. AVL树的查找
AVL树的查找逻辑就与二叉搜索树一样了,这里就不在赘述。
Node* Find(const K& val)
{Node* cur = _root;while (cur){if (cur->_kv.first > val){//左子树中查找cur = cur->_left;}else if (cur->_kv.first < val){//右子树中查找cur = cur->_right;}else{//找到了return cur;}}return nullptr;
}
5.4. AVL树的删除
AVL树的删除逻辑其实整体与二叉搜索树的删除逻辑类似,可以分为三种情况讨论:删除节点的左子树节点为空
,删除节点的右子树节点为空,删除节点的左右子树都不为空。其中删除节点的左右子树都不为空可以经过伪删除法,即寻找到左子树的最右节点即左子树的最大值,或者是右子树的最左节点即右子树的最小值。然后赋值,转换为在其左子树或者右子树删除节点。而我们的AVL树本质是为了保持平衡,所以尽量选择删除子树较高的一方。
因为删除节点的左右子树都不为空的情况一定会被转换另外两种情况,所以我们只需要讨论删除节点的左子树节点为空,删除节点的右子树节点为空这两种情况。
当然这里在上面基础上再重新分类可分为:
- 删除节点在父节点的左侧:
当节点数少于三个时,删除后父节点平衡因子为1或0时,正常删除。
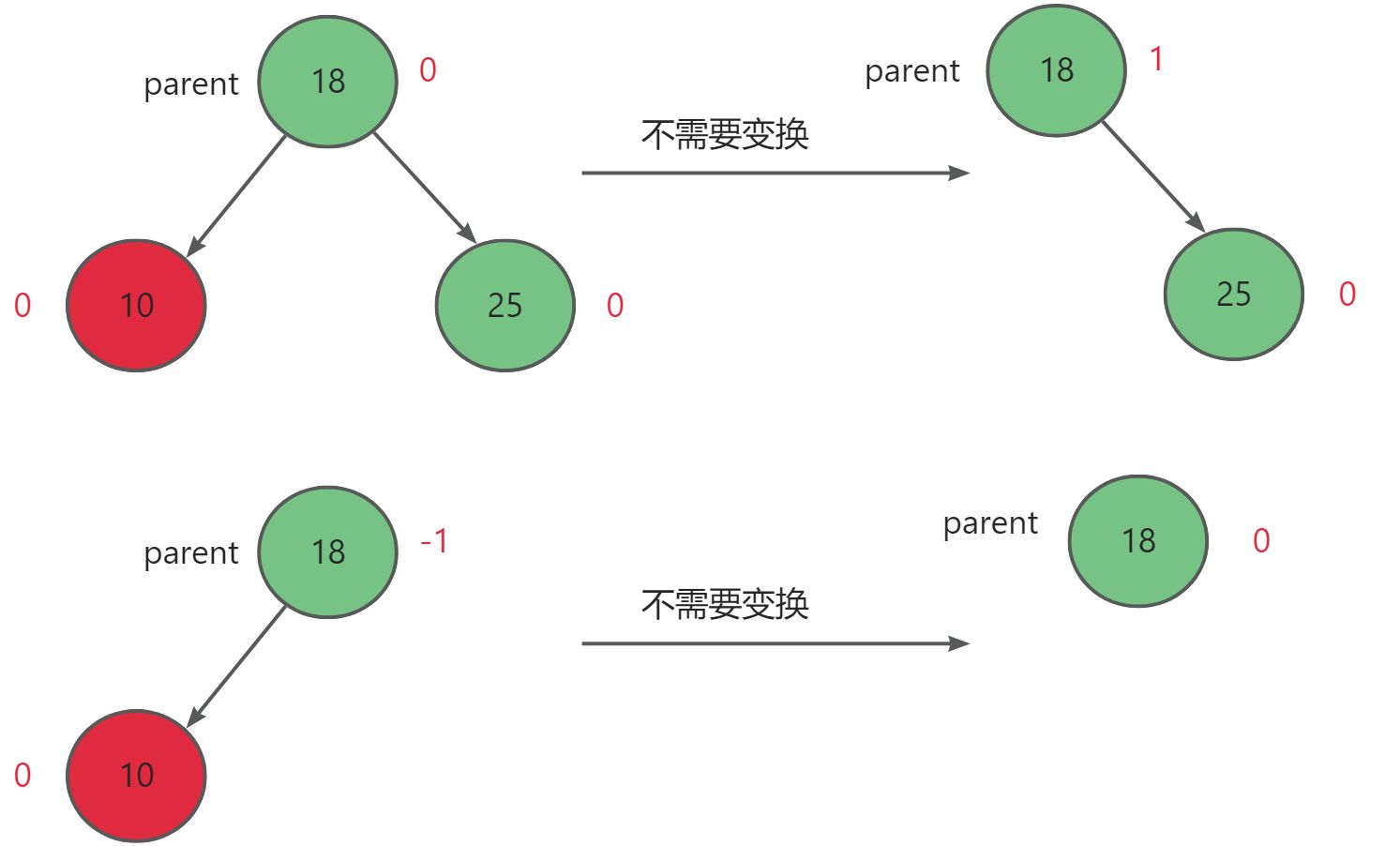
当父节点parent的右子树的左右子树高度相等,且删除后父节点平衡因子为2时,进行左单旋。
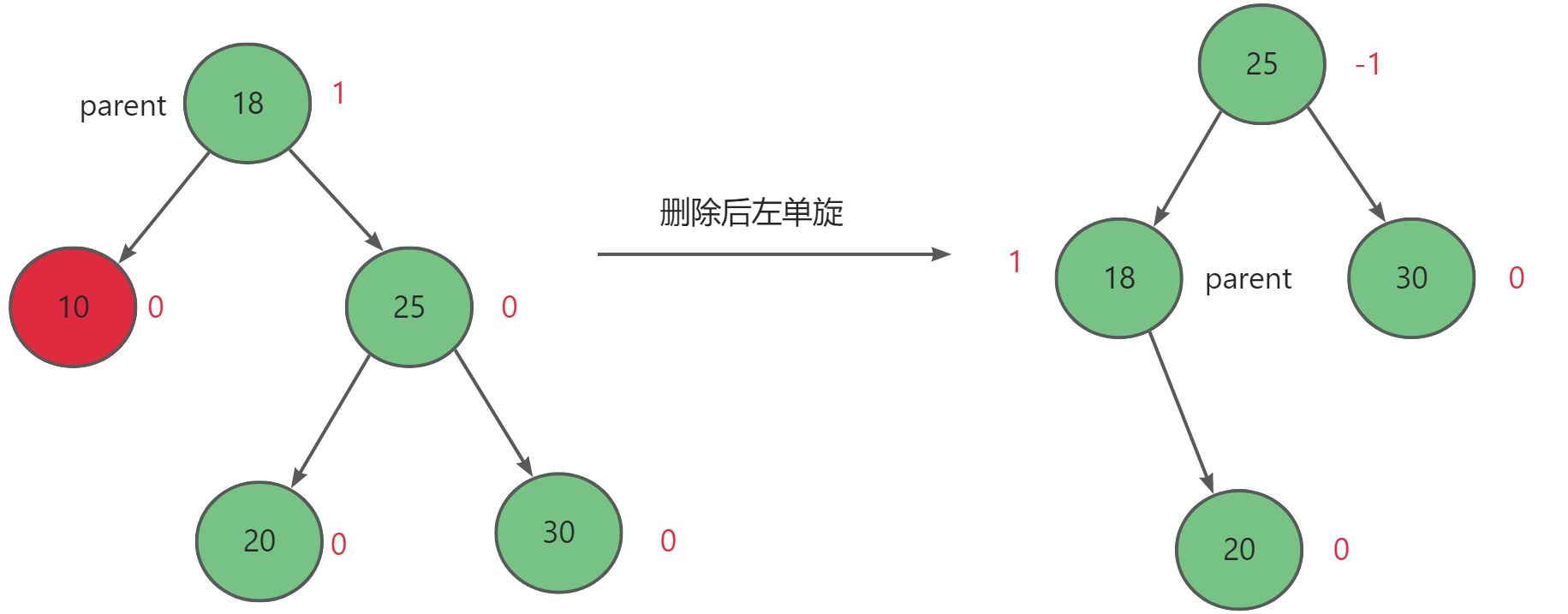
当父节点parent的右子树的右子树高度大于其左子树高度,且删除后父节点平衡因子为2时,进行左单旋。
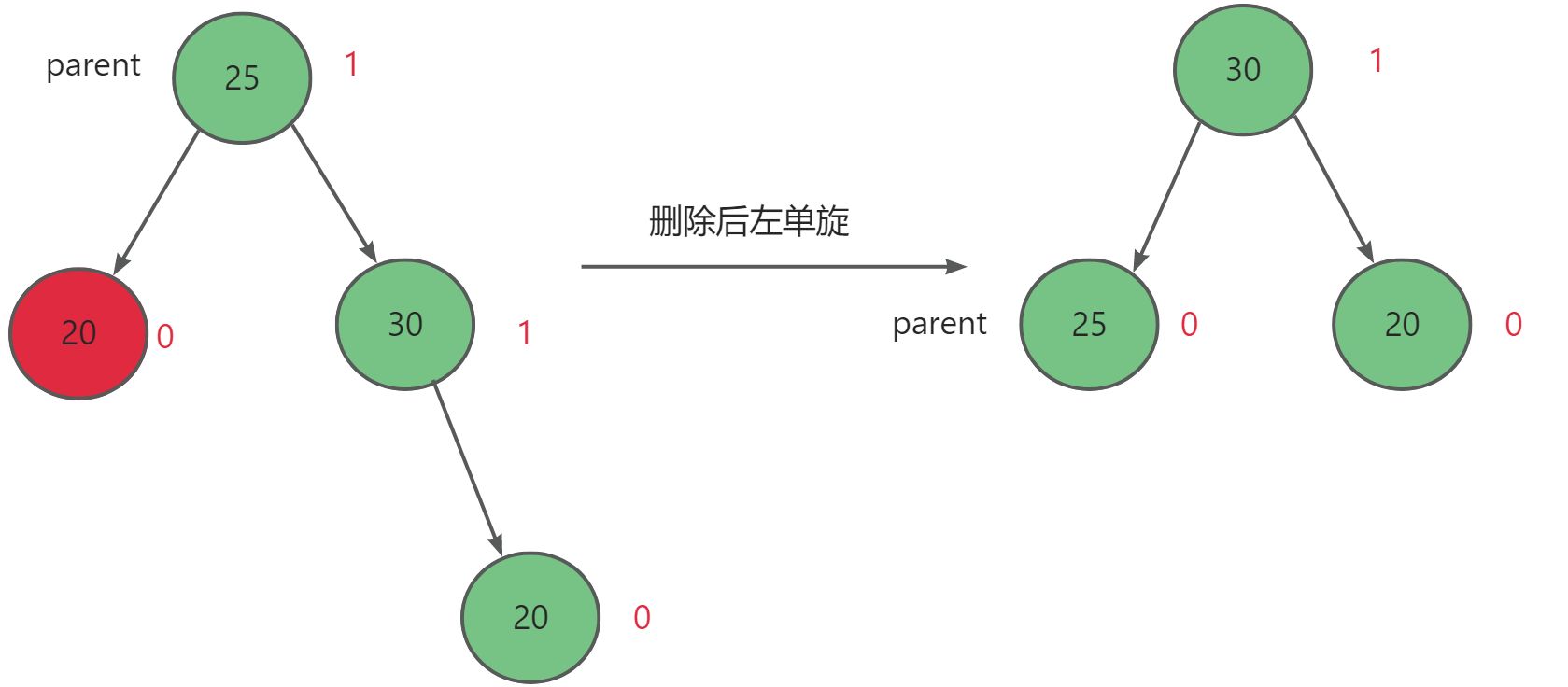
当父节点parent的右子树的右子树高度小于其左子树高度,且删除后父节点平衡因子为2时,先进行右单旋,再进行左单旋。
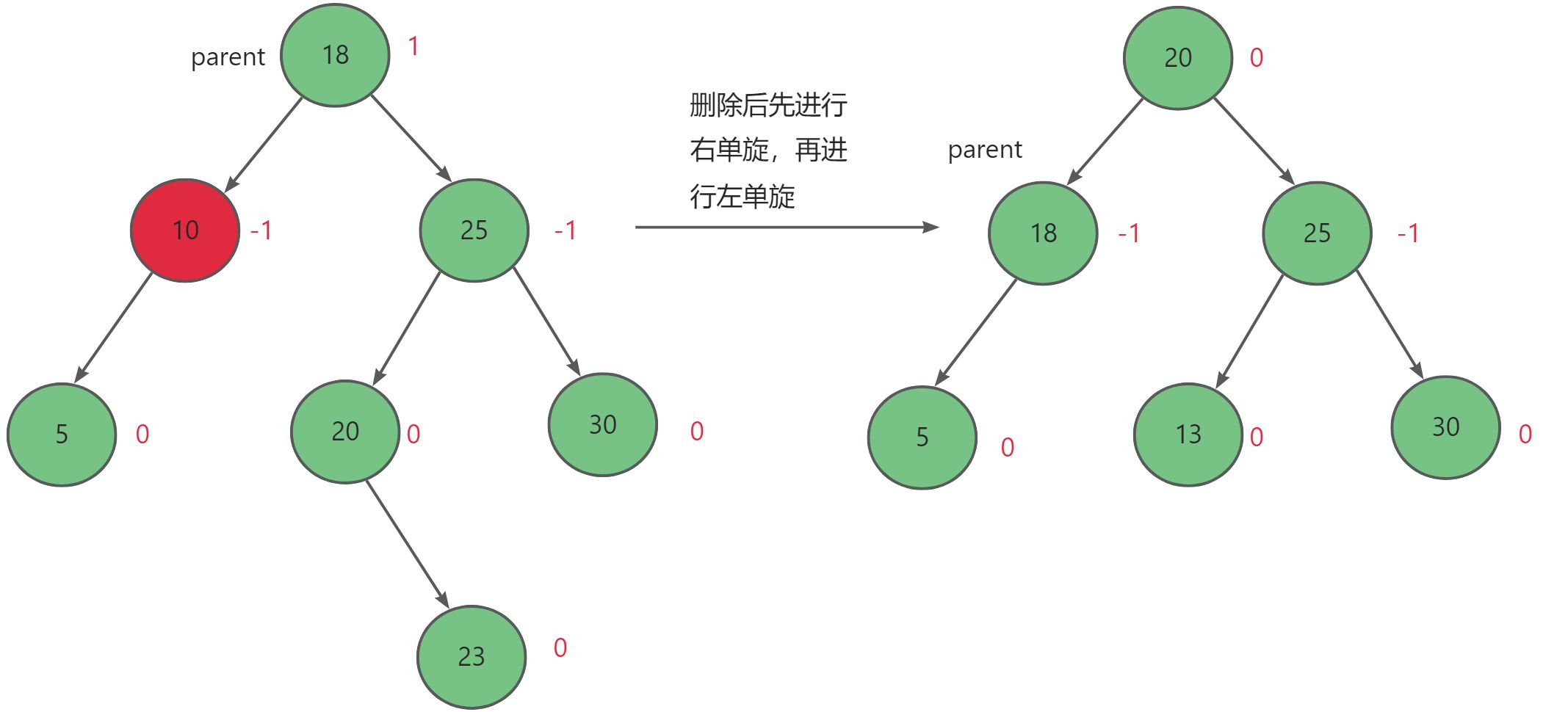
- 删除节点在父节点右侧:
当节点数少于三个时,删除后父节点平衡因子为-1或0时,正常删除。
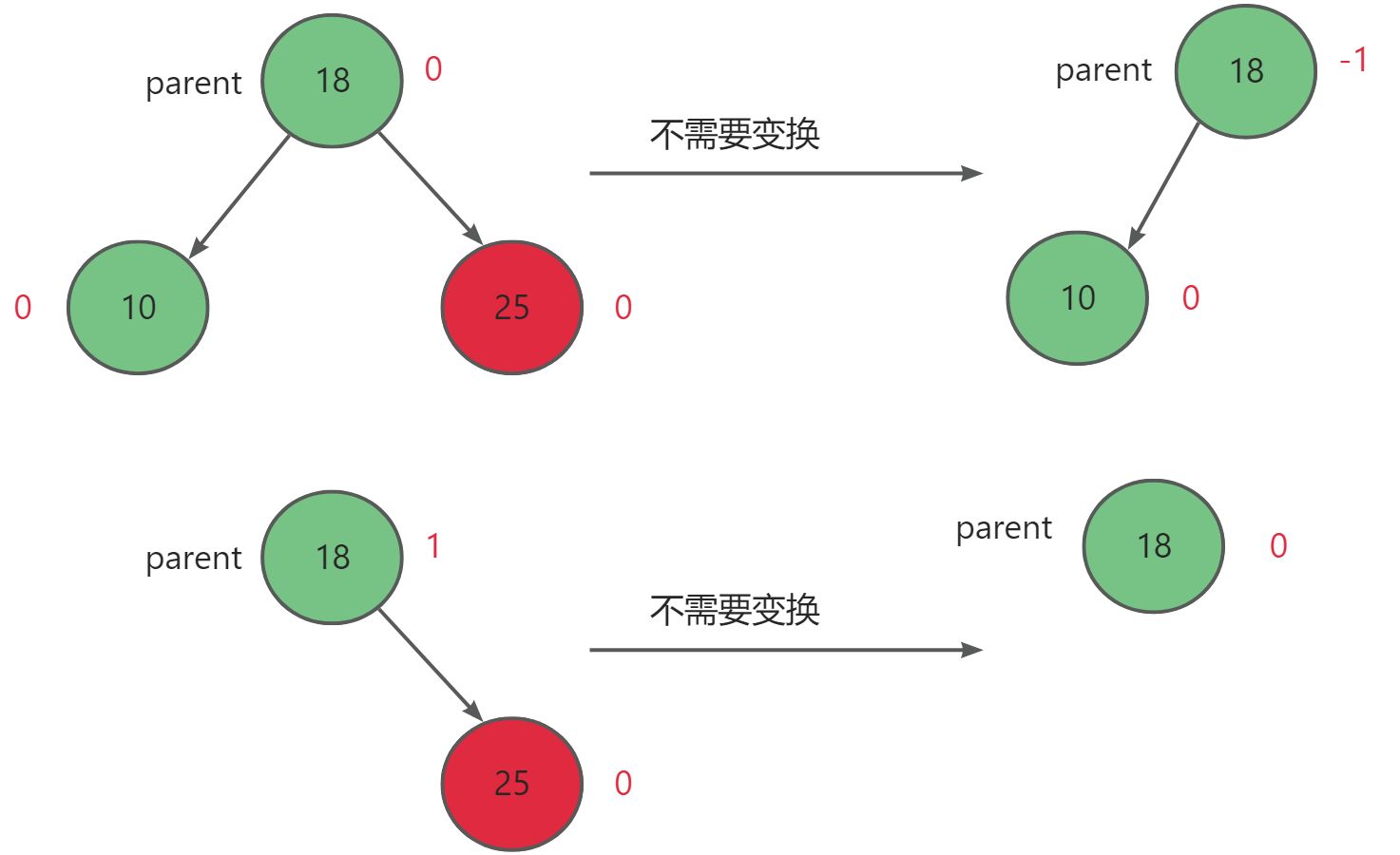
当父节点parent的左子树的左右子树高度相等,且删除后父节点平衡因子为-2时,进行右单旋。
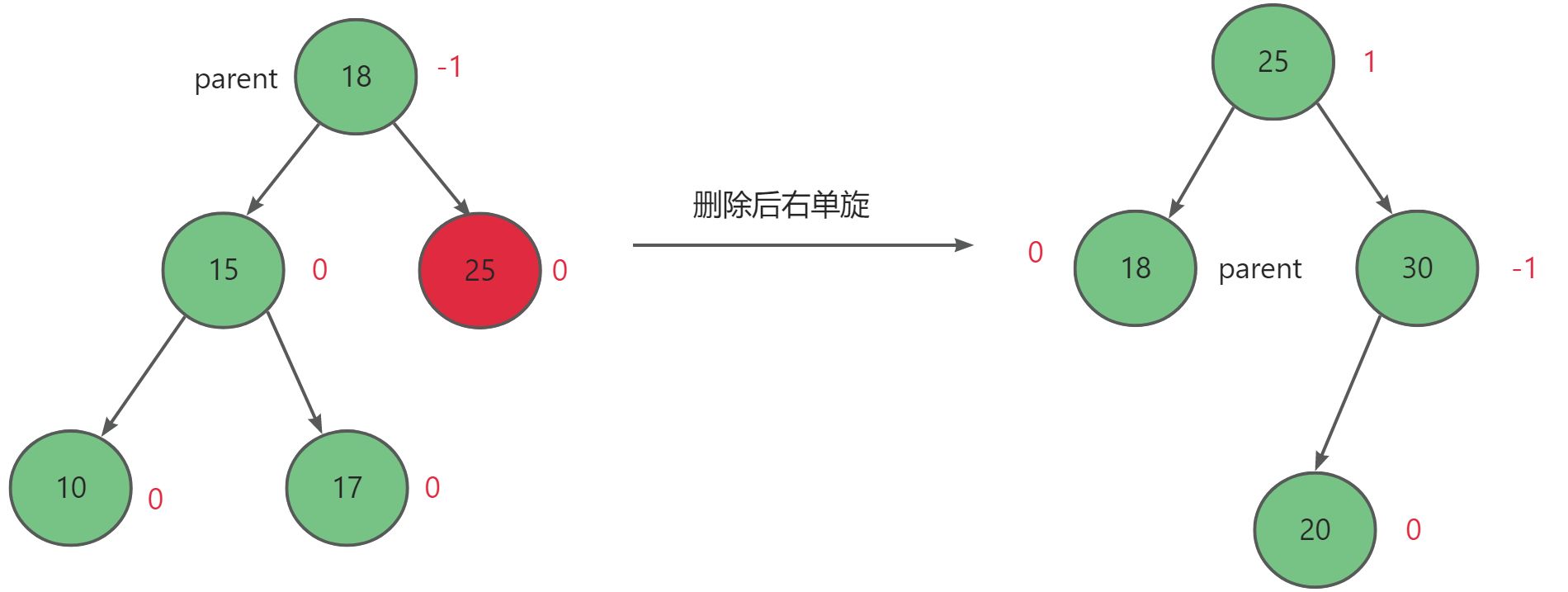
当父节点parent的左子树的左子树高度大于其右子树高度,且删除后父节点平衡因子为-2时,进行右单旋。
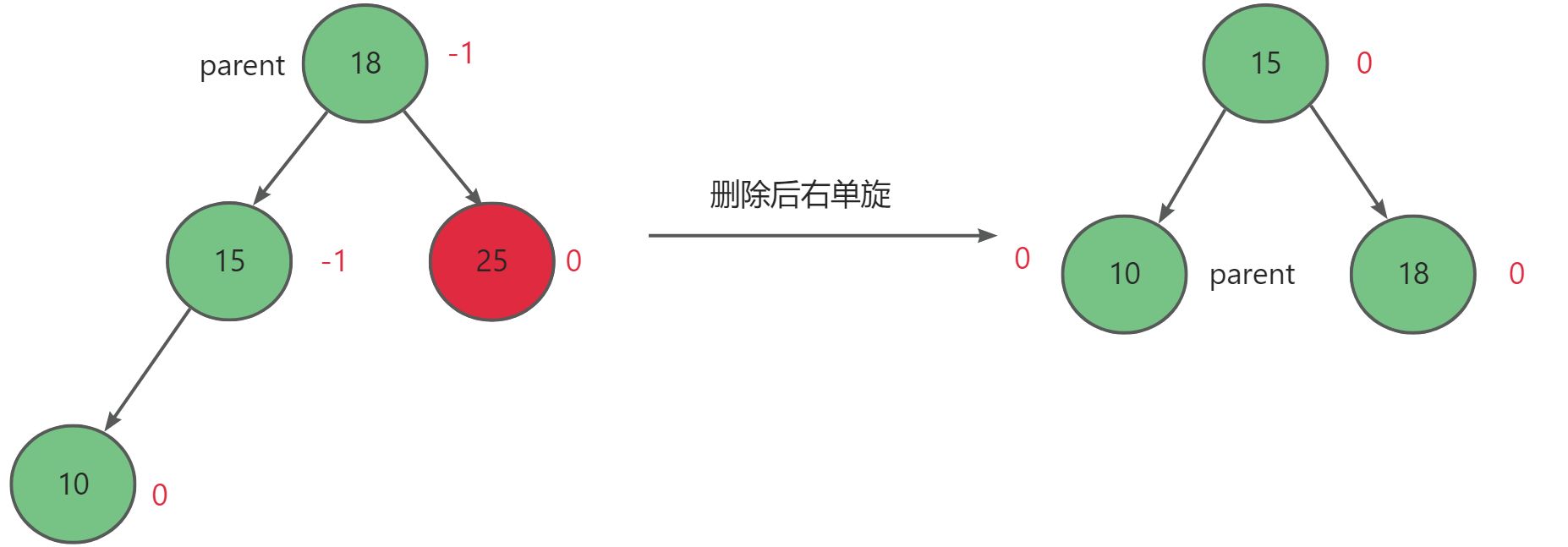
当父节点parent的左子树的左子树高度小于其右子树高度,且删除后父节点平衡因子为-2时,先进行左单旋,再进行右单旋。
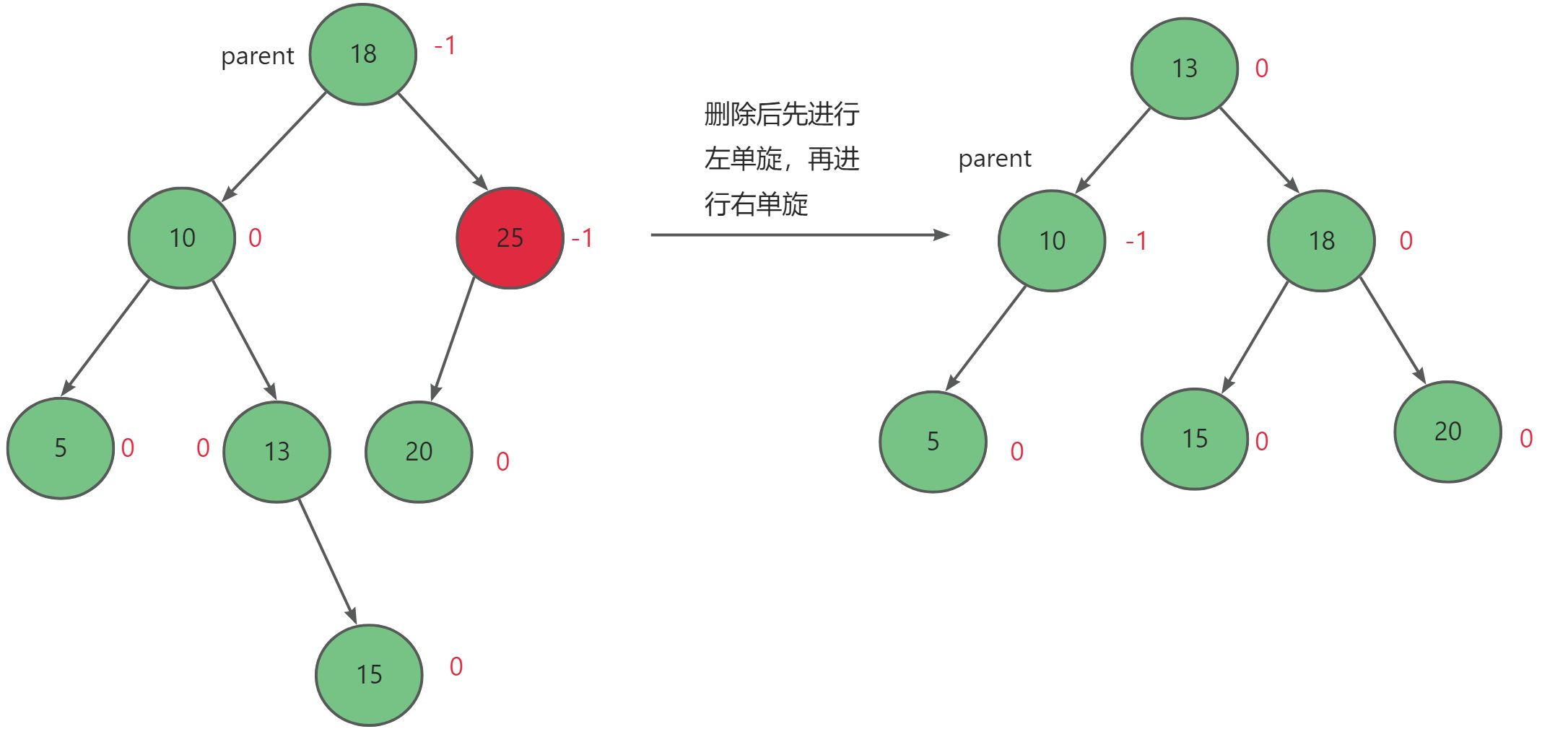
最后我们可以总结出以下结论:
- 当删除节点在父节点的左侧时
- 父节点的平衡因子为2时,如果根节点的右子树的右子树高度大于等于其左子树高度,进行左单旋,否则进行先右旋再左旋。
- 父节点的平衡因子不为2时,正常删除。
- 当删除节点在父节点的右侧时
- 父节点的平衡因子为-2时,如果根节点的左子树的左子树高度大于等于其右子树高度,进行右单旋,否则进行先左旋再右旋。
- 父节点的平衡因子不为-2时,正常删除。
//求高度
int Hegiht(Node* root)
{if (root == nullptr)return 0;int leftHegiht = Hegiht(root->_left);//先计算左子树高度int rightHegiht = Hegiht(root->_right);//再计算右子树高度return leftHegiht > rightHegiht ? leftHegiht + 1 : rightHegiht + 1;
}
void erase(const K& val)
{//递归删除_root = _erase(_root, val);
}
Node* _erase(Node* node, const K& val)
{// 如果当前节点为空,直接返回空指针if (node == nullptr){return nullptr;}// 如果当前节点的键值大于要删除的键值,在左子树中删除if (node->_kv.first > val){node->_left = _erase(node->_left, val);//更新节点的父节点if (node->_left)node->_left->_parent = node;// 调整节点的平衡因子node->_bf = Hegiht(node->_right) - Hegiht(node->_left);int bf = node->_bf;//情况一删除节点都在左边if (bf == 2){int rightHegiht = Hegiht(node->_right->_right);int leftHegiht = Hegiht(node->_right->_left);if (rightHegiht >= leftHegiht){RotateL(node);}else{RotateRL(node);}}}// 如果当前节点的键值小于要删除的键值,在右子树中删除else if (node->_kv.first < val){node->_right = _erase(node->_right, val);//更新节点的父节点if(node->_right)node->_right->_parent = node;// 调整节点平衡因子node->_bf = Hegiht(node->_right) - Hegiht(node->_left);int bf = node->_bf;//情况二删除节点都在右边if (bf == -2){int rightHegiht = Hegiht(node->_left->_right);int leftHegiht = Hegiht(node->_left->_left);if (leftHegiht >= rightHegiht){RotateR(node);}else{RotateLR(node);}}}// 找到要删除的节点else{// 如果节点有两个孩子if (node->_left != nullptr && node->_right != nullptr){// 如果左子树高度大于等于右子树高度if (Hegiht(node->_left) >= Hegiht(node->_right)){// 找到左子树中的最大节点Node* prev = node->_left;while (prev->_right)prev = prev->_right;int target = prev->_kv.first;// 将当前节点的值替换为左子树中的最大节点的值node->_kv = prev->_kv;// 在左子树中删除该最大节点node->_left = _erase(node->_left,target);}else{// 找到右子树中的最小节点Node* post = node->_right;while (post->_left)post = post->_left;// 将当前节点的值替换为右子树中的最小节点的值int target = post->_kv.first;node ->_kv = post->_kv ;// 在右子树中删除该最小节点node->_right = _erase(node->_right, target);}}// 如果节点最多有一个孩子else{// 如果有左孩子if (node->_left != nullptr){// 保存左孩子指针Node* left = node->_left;// 删除当前节点delete node;// 返回左孩子指针return left;}// 如果有右孩子else if (node->_right != nullptr){// 保存右孩子指针Node* right = node->_right;// 删除当前节点delete node;// 返回右孩子指针return right;}// 如果没有孩子else{// 返回空指针delete node;return nullptr;}}}// 返回调整后的节点指针return node;
}
6. 判断是否为AVL树
在判断一棵树是否为 AVL 树时,其核心在于检查每一个节点的左右子树高度差的绝对值是否小于 1 。由于需要对整棵树的所有子树进行这样的判断,所以采用递归的方法比较合适的。
具体实现时,定义一个函数来进行判断。然后,分别递归地获取左子树和右子树的高度。接着,进行条件判断。如果左子树或右子树中存在高度标记为 -1 的情况(意味着该子树不平衡),或者当前节点左右子树高度差的绝对值大于 1 ,那么就将当前子树的高度标记为 -1 并返回。如果当前节点的子树都是平衡的,那么就返回最高的高度。
最后,通过一个总函数来调用这个递归函数,并根据返回结果是否大于 0 来确定整棵树是否为 AVL 树。如果大于 0 ,则表示整棵树是AVL 树;否则,表示不是AVL树。
//判断是否平衡
bool isBalanced()
{return _isBalanced(_root) >= 0;
}
int _isBalanced(Node* root)
{if (root == nullptr){return 0;}//左平衡高度int left_isBalanced = _isBalanced(root->_left);//右平衡高度int right_isBalanced = _isBalanced(root->_right);//如果右平衡-左平衡则返回-1,并且防止两边同时返回-1相减等于0的情况,需要单独判断if (left_isBalanced == -1 || right_isBalanced == -1 || abs(right_isBalanced - left_isBalanced) > 1){return -1;}//返回最高高度return max(left_isBalanced, right_isBalanced) + 1;
}
7. 复杂度分析
下是对上述AVL 树代码中主要操作的时间复杂度和空间复杂度分析:
时间复杂度:
insert操作:平均和最坏情况下的时间复杂度均为 O ( log n ) O(\log n) O(logn)。在插入过程中,通过不断调整平衡因子和进行旋转操作来保持树的平衡,每次调整和旋转的操作时间都是常数级,而查找插入位置的过程类似于二叉搜索树,时间复杂度为
O ( log n ) O(\log n) O(logn)。Find操作:平均和最坏情况下的时间复杂度均为 O ( log n ) O(\log n) O(logn)。与二叉搜索树的查找过程类似,每次比较都将搜索范围缩小一半。erase操作:平均和最坏情况下的时间复杂度均为 O ( log n ) O(\log n) O(logn)。删除节点时需要查找节点位置,然后进行调整和可能的旋转操作,时间复杂度类似于插入操作。
空间复杂度:
insert操作:空间复杂度为 O ( 1 ) O(1) O(1)。在插入过程中,主要的额外空间消耗在于创建新节点以及一些临时变量来存储指针和平衡因子等信息,这些都是常数级的空间消耗。Find操作:空间复杂度为 O ( 1 ) O(1) O(1)。在查找过程中,仅使用了一些固定数量的指针和临时变量,没有额外的大规模空间分配。erase操作:空间复杂度为 O ( 1 ) O(1) O(1)。删除操作中,主要的空间消耗在于临时变量和指针的存储,没有动态分配大规模的额外空间。总的来说,上述各个操作的主要空间复杂度都为 O ( 1 ) O(1) O(1),整个 AVL 树的空间复杂度主要取决于树中节点的数量,即 O ( n ) O(n) O(n),其中 n n n 是节点的数量。
8. 源码
#pragma once
#include<utility>
#include<assert.h>
template<class K,class V>
struct AVLTreeNode
{AVLTreeNode(const pair<K, V>& val = pair<K, V>()):_kv(val),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}pair<K, V> _kv;//kv模型int _bf;//平衡因子AVLTreeNode* _left;//左子树AVLTreeNode* _right;//右子树AVLTreeNode* _parent;//指向父节点
};
template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://...具体功能AVLTree(){}AVLTree(const AVLTree& t){_root = copy(t._root);}AVLTree<K,V>& operator=(const AVLTree <K,V> t){//赋值重载this->swap(_root, t._root);return *this;}void RotateR(Node*&parent){// 获取父节点的左子节点Node* subL = parent->_left;// 获取父节点左子节点的右子节点Node* subLR = subL->_right;// 1.将subLR链接到parent的左边。parent->_left = subLR;// 如果父节点左子节点的右子节点存在,设置其父节点为当前父节点if (subLR){subLR->_parent = parent;}// 获取父节点的父节点Node* ppNode = parent->_parent;// 2.将parent链接到subL的右边。subL->_right = parent;//parent的父节点指向subLparent->_parent = subL;// 如果父节点存在父节点if (ppNode){// 如果父节点是其父亲节点的左子节点if (ppNode->_left == parent){// 将父节点的父亲节点的左子节点设置为当前父节点的左子节点ppNode->_left = subL;}// 如果父节点是其父亲节点的右子节点else{// 将父节点的父亲节点的右子节点设置为当前父节点的左子节点ppNode->_right = subL;}// 设置父节点左子节点的父节点为父节点的父节点subL->_parent = ppNode;}// 如果父节点为根节点else{// 将根节点设置为父节点的左子节点_root = subL;// 将父节点左子节点的父节点设置为空subL->_parent = nullptr;}//3.将parent与subL的平衡因子置为0。subL->_bf = parent->_bf = 0;//改变parent节点的指向,方便erase中的node返回parent = subL;}void RotateL(Node* &parent){// 获取父节点的右子节点Node* subR = parent->_right;// 获取父节点右子节点的左子节点Node* subRL = subR->_left;//1.将subRL链接到parent的右边。parent->_right = subRL;// 如果父节点右子节点的左子节点存在,设置其父节点为当前父节点if (subRL){subRL->_parent = parent;}// 获取父节点的父节点Node* ppNode = parent->_parent;//2.将parent链接到subR的左边。subR->_left = parent;// 设置父节点的父节点为右子节点parent->_parent = subR;// 如果父节点存在父节点if (ppNode){// 如果父节点是其父亲节点的左子节点if (ppNode->_left == parent){// 将父节点的父亲节点的左子节点设置为当前父节点的右子节点ppNode->_left = subR;}// 如果父节点是其父亲节点的右子节点else{// 将父节点的父亲节点的右子节点设置为当前父节点的右子节点ppNode->_right = subR;}// 设置父节点右子节点的父节点为父节点的父节点subR->_parent = ppNode;}// 如果父节点为根节点else{// 将根节点设置为父节点的右子节点_root = subR;// 将父节点右子节点的父节点设置为空subR->_parent = nullptr;}// 3.将parent与subR的平衡因子置为0。subR->_bf = parent->_bf = 0;//改变parent节点的指向,方便erase中的node返回parent = subR;}void RotateLR(Node*&parent){Node* subL = parent->_left;Node* subLR = subL->_right;//先左旋RotateL(parent->_left);//再右旋RotateR(parent);int bf = subLR->_bf;//1.情况1if (bf == 0){parent->_bf = subL->_bf = subLR->_bf = 0;}//2.情况2else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}//3.情况3else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{//走到这里说明AVL树有问题assert(false);}}void RotateRL(Node*&parent){Node* subR = parent->_right;Node* subRL = subR->_left;//先右单旋RotateR(parent->_right);//再左单旋RotateL(parent);int bf = subRL->_bf;//1.情况一if (bf == 0){parent->_bf = subRL->_bf = subR->_bf = 0;}//2.情况二else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}//3.情况三else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else{//走到这里说明AVL树出错assert(false);}}bool insert(const pair<K, V>& kv){// 如果根节点为空,创建新节点作为根节点并设置平衡因子为 0,然后返回插入成功if (_root == nullptr){_root = new Node(kv);_root->_bf = 0;return true;}// 初始化父节点为空,当前节点为根节点Node* parent = nullptr;Node* cur = _root;// 查找插入位置while (cur){// 小于当前节点,往左子树if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}// 大于当前节点,往右子树else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}// 键已存在,返回插入失败else{return false;}}// 找到插入位置,创建新节点cur = new Node(kv);// 根据键值大小确定新节点在父节点的位置if (kv.first > parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 更新平衡因子while (parent){// 如果插入在左边,父节点的平衡因子减 1if (cur == parent->_left){parent->_bf--;}// 如果插入在右边,父节点的平衡因子加 1else{parent->_bf++;}// 如果父节点平衡因子为 0,整体高度不变,不需要再向上调整if (parent->_bf == 0){break;}// 平衡因子为 1 或 -1,需要继续向上调整else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}// 平衡因子为 -2 或 2,需要进行旋转操作以保持平衡else if (parent->_bf == -2 || parent->_bf == 2){// 右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}// 左单旋else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}// 左右双旋else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}// 右左双旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}// 插入之前 AVL 树就已经不平衡了,断言else{assert(false);}}return true;}Node* Find(const K& val){Node* cur = _root;while (cur){if (cur->_kv.first > val){//左子树中查找cur = cur->_left;}else if (cur->_kv.first < val){//右子树中查找cur = cur->_right;}else{//找到了return cur;}}return nullptr;}//求高度int Hegiht(Node* root){if (root == nullptr)return 0;int leftHegiht = Hegiht(root->_left);//先计算左子树高度int rightHegiht = Hegiht(root->_right);//再计算右子树高度return leftHegiht > rightHegiht ? leftHegiht + 1 : rightHegiht + 1;}void erase(const K& val){//递归删除_root = _erase(_root, val);}//判断是否平衡bool isBalanced(){return _isBalanced(_root) >= 0;}~AVLTree(){Destroy(_root);}private:void Destroy(Node* root){if (root == nullptr){return;}//cout << root->_kv.first << " ";//递归销毁左子树Destroy(root->_left);//递归销毁右子树Destroy(root->_right);//销毁根节点delete root;//root = nullptr;}Node* _erase(Node* node, const K& val){// 如果当前节点为空,直接返回空指针if (node == nullptr){return nullptr;}// 如果当前节点的键值大于要删除的键值,在左子树中删除if (node->_kv.first > val){node->_left = _erase(node->_left, val);//更新节点的父节点if (node->_left)node->_left->_parent = node;// 调整节点的平衡因子node->_bf = Hegiht(node->_right) - Hegiht(node->_left);int bf = node->_bf;//情况一删除节点都在左边if (bf == 2){int rightHegiht = Hegiht(node->_right->_right);int leftHegiht = Hegiht(node->_right->_left);if (rightHegiht >= leftHegiht){RotateL(node);}else{RotateRL(node);}}}// 如果当前节点的键值小于要删除的键值,在右子树中删除else if (node->_kv.first < val){node->_right = _erase(node->_right, val);//更新节点的父节点if(node->_right)node->_right->_parent = node;// 调整节点平衡因子node->_bf = Hegiht(node->_right) - Hegiht(node->_left);int bf = node->_bf;//情况二删除节点都在右边if (bf == -2){int rightHegiht = Hegiht(node->_left->_right);int leftHegiht = Hegiht(node->_left->_left);if (leftHegiht >= rightHegiht){RotateR(node);}else{RotateLR(node);}}}// 找到要删除的节点else{// 如果节点有两个孩子if (node->_left != nullptr && node->_right != nullptr){// 如果左子树高度大于等于右子树高度if (Hegiht(node->_left) >= Hegiht(node->_right)){// 找到左子树中的最大节点Node* prev = node->_left;while (prev->_right)prev = prev->_right;int target = prev->_kv.first;// 将当前节点的值替换为左子树中的最大节点的值node->_kv = prev->_kv;// 在左子树中删除该最大节点node->_left = _erase(node->_left,target);}else{// 找到右子树中的最小节点Node* post = node->_right;while (post->_left)post = post->_left;// 将当前节点的值替换为右子树中的最小节点的值int target = post->_kv.first;node ->_kv = post->_kv ;// 在右子树中删除该最小节点node->_right = _erase(node->_right, target);}}// 如果节点最多有一个孩子else{// 如果有左孩子if (node->_left != nullptr){// 保存左孩子指针Node* left = node->_left;// 删除当前节点delete node;// 返回左孩子指针return left;}// 如果有右孩子else if (node->_right != nullptr){// 保存右孩子指针Node* right = node->_right;// 删除当前节点delete node;// 返回右孩子指针return right;}// 如果没有孩子else{// 返回空指针delete node;return nullptr;}}}// 返回调整后的节点指针return node;}int _isBalanced(Node* root){if (root == nullptr){return 0;}//左平衡高度int left_isBalanced = _isBalanced(root->_left);//右平衡高度int right_isBalanced = _isBalanced(root->_right);//如果右平衡-左平衡则返回-1,并且防止两边同时返回-1相减等于0的情况,需要单独判断if (left_isBalanced == -1 || right_isBalanced == -1 || abs(right_isBalanced - left_isBalanced) > 1){return -1;}//返回最高高度return max(left_isBalanced, right_isBalanced) + 1;}Node* copy(Node* root){// 如果传入的根节点为空,直接返回空指针,表示拷贝结束if (root == nullptr)return nullptr;// 为新树创建一个与原始根节点值相同的新节点Node* newnode = new Node(root->_kv);// 递归地拷贝原始根节点的左子树,并将结果赋给新节点的左指针newnode->_left = copy(root->_left);// 递归地拷贝原始根节点的右子树,并将结果赋给新节点的右指针newnode->_right = copy(root->_right);// 新节点的父节点默认为空newnode->_parent = nullptr;// 如果新节点的左子节点存在,设置其父节点为新节点if (newnode->_left){newnode->_left->_parent = newnode;}// 如果新节点的右子节点存在,设置其父节点为新节点if (newnode->_right){newnode->_right->_parent = newnode;}// 返回新树的根节点指针return newnode;}Node* _root = nullptr;//根节点
};}// 如果有右孩子else if (node->_right != nullptr){// 保存右孩子指针Node* right = node->_right;// 删除当前节点delete node;// 返回右孩子指针return right;}// 如果没有孩子else{// 返回空指针delete node;return nullptr;}}}// 返回调整后的节点指针return node;}int _isBalanced(Node* root){if (root == nullptr){return 0;}//左平衡高度int left_isBalanced = _isBalanced(root->_left);//右平衡高度int right_isBalanced = _isBalanced(root->_right);//如果右平衡-左平衡则返回-1,并且防止两边同时返回-1相减等于0的情况,需要单独判断if (left_isBalanced == -1 || right_isBalanced == -1 || abs(right_isBalanced - left_isBalanced) > 1){return -1;}//返回最高高度return max(left_isBalanced, right_isBalanced) + 1;}Node* copy(Node* root){// 如果传入的根节点为空,直接返回空指针,表示拷贝结束if (root == nullptr)return nullptr;// 为新树创建一个与原始根节点值相同的新节点Node* newnode = new Node(root->_kv);// 递归地拷贝原始根节点的左子树,并将结果赋给新节点的左指针newnode->_left = copy(root->_left);// 递归地拷贝原始根节点的右子树,并将结果赋给新节点的右指针newnode->_right = copy(root->_right);// 新节点的父节点默认为空newnode->_parent = nullptr;// 如果新节点的左子节点存在,设置其父节点为新节点if (newnode->_left){newnode->_left->_parent = newnode;}// 如果新节点的右子节点存在,设置其父节点为新节点if (newnode->_right){newnode->_right->_parent = newnode;}// 返回新树的根节点指针return newnode;}Node* _root = nullptr;//根节点
};
相关文章:

探索数据结构:AVL树的分析与实现
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty’s blog 1. AVL树的介绍 在前面我们学习二叉搜索树时知道,在数据有序…...

使用 C++ 实现简单的插件系统
使用 C 实现简单的插件系统 在现代软件开发中,插件系统是一种常见的架构模式,它允许开发者在不修改主程序的情况下,扩展应用程序的功能。通过插件,用户可以根据需要添加或移除功能模块,从而提高软件的灵活性和可维护性…...

使用Python创建省份城市地图选择器
在这篇博客中,我们将探讨如何使用Python创建一个简单而实用的省份城市地图选择器。这个项目不仅能帮助我们学习Python的基础知识,还能让我们了解如何处理JSON数据和集成网页浏览器到桌面应用程序中。 C:\pythoncode\new\geographicgooglemap.py 全部代码…...

【Java 数据结构】Stack和Queue介绍
Stack和Queue StackStack是什么Stack的使用构造方法常用方法 栈的模拟实现初始化和基本方法入栈出栈查看栈顶 栈的应用链栈的简单介绍 QueueQueue是什么Queue的使用队列的模拟实现初始化入队出队查看队头元素 循环队列循环队列的定义及其注意点循环队列的实现初始化和基本方法获…...
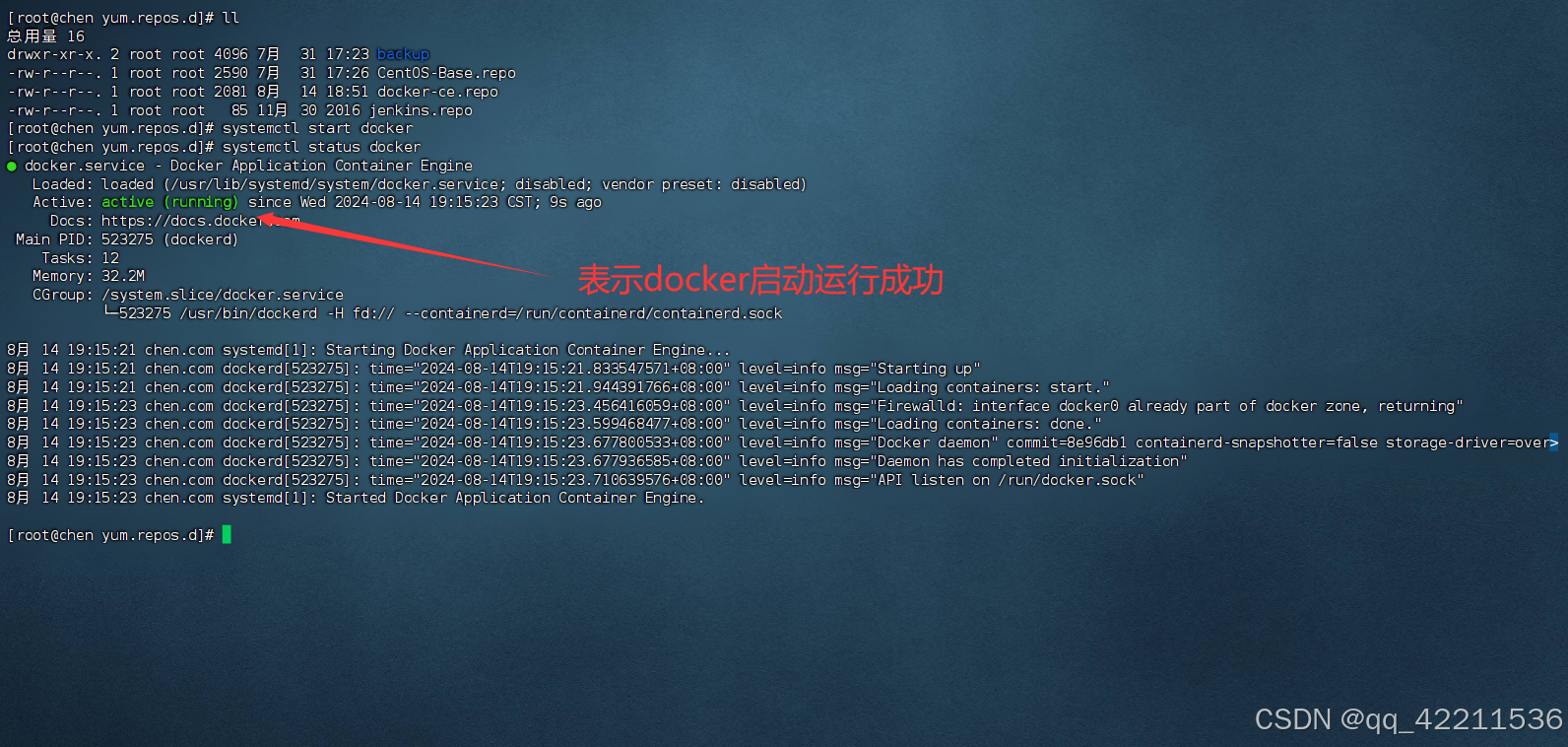
Docker基本语法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、更新yum镜像仓库(一)查看本地yum镜像源地址(二)设置docker的镜像仓库(1)安装必要工具…...

uniapp 对于scroll-view滑动和页面滑动的联动处理
需求 遇到一个需求 解决方案 这个时候可以做一个内页面滑动判断 <!-- scroll-y 做true或者false的判断是否滑动 --> <view class"u-menu-wrap" style"background-color: #fff;"><scroll-view :scroll-y"data.isGo" scroll-wit…...

opencv基础的图像操作
1.读取图像,显示图像,保存图像 #图像读取、显示与保存 import numpy as np import cv2 imgcv2.imread(./src/1.jpg) #读取 cv2.imshow("img",img) #显示 cv2.imwrite("./src/2.jpg",img) #保存 cv2.waitKey(0) #让程序进入主循环(让…...

Java | Leetcode Java题解之第337题打家劫舍III
题目: 题解: class Solution {public int rob(TreeNode root) {int[] rootStatus dfs(root);return Math.max(rootStatus[0], rootStatus[1]);}public int[] dfs(TreeNode node) {if (node null) {return new int[]{0, 0};}int[] l dfs(node.left);i…...

本地查看的Git远程仓库分支与远程仓库分支数量不一致
说明:一次,在IDEA中想切换到某分支,但是查看Remote没有找到要切换的分支,但是打开GitLab,查看远程仓库,是有这个分支的。 解决:1)在IDEA的Git中,点下面Fatch获取一下远程…...

opencv-python实战项目九:基于拉普拉斯金字塔的图像融合
文章目录 一,简介:二,拉普拉斯金字塔介绍:三,算法实现步骤3.1 构建融合拉普拉斯金字塔3.2 融合后的拉普拉斯金字塔复原: 四,整体代码实现:五,效果: 一&#x…...

浅谈JDK
JDK(Java Development Kit) JDK是Java开发工具包,是Java编程语言的核心软件开发工具。 JDK包含了一系列用于开发、编译和运行Java应用程序的工具和资源。其中包括: 1.Java编译器(javac):用于将Java源代码编译成字节…...

爬虫案例3——爬取彩票双色球数据
简介:个人学习分享,如有错误,欢迎批评指正 任务:从500彩票网中爬取双色球数据 目标网页地址:https://datachart.500.com/ssq/ 一、思路和过程 目标网页具体内容如下: 我们的任务是将上图中…...

C++ | Leetcode C++题解之第337题打家劫舍III
题目: 题解: struct SubtreeStatus {int selected;int notSelected; };class Solution { public:SubtreeStatus dfs(TreeNode* node) {if (!node) {return {0, 0};}auto l dfs(node->left);auto r dfs(node->right);int selected node->val…...

软件架构设计师-UML知识导图
软件架构设计师-UML知识导图,包含如下内容: 结构化设计,包含结构化设计的概念、结构化设计的主要内容、概要设计、详细设计及模块设计原则;UML是什么:介绍UML是什么;UML的结构:构造块、公共机制…...

在使用transformers和pytorch时出现的版本冲突的问题
在使用transformers和torch库的时候,出现了以下问题: 1、OSError: [WinError 126] 找不到指定的模块。 Error loading "D:\Program Files\anaconda3\envs\testenv\Lib\site-packages\torch\lib\fbgemm.dll" or one of its dependencies. 2、…...

uniapp粘贴板地址识别
1: 插件安装 主要是依靠 address-parse 这个插件: 官网 收货地址自动识别 支持pc、h5、微信小程序 - DCloud 插件市场 // 首先需要引入插件 npm install address-parse --save 2:html部分 <view class""><view class&quo…...

C语言 | Leetcode C语言题解之第335题路径交叉
题目: 题解: bool isSelfCrossing(int* distance, int distanceSize){if (distance NULL || distanceSize < 4) {return false;}for (int i 3; i < distanceSize; i) {if ((distance[i] > distance[i - 2]) && (distance[i - 1] &l…...

TypeScript学习第十三篇 - 泛型
在编译期间不确定变量的类型,在调用时,由开发者指定具体的类型。 1. 如何给arg参数和函数指定类型? function identity(arg){return arg; }identity(1) identity(jack) identity(true) identity([]) identity(null)定义的时候,无…...

工业智能网关在汽车制造企业的应用价值及功能-天拓四方
随着工业互联网的飞速发展,工业智能网关作为连接物理世界与数字世界的桥梁,正逐渐成为制造业数字化转型的核心组件。本文将以一家汽车制造企业的实际使用案例为蓝本,深入解析工业智能网关在实际应用中的价值、功能及其实操性。 一、背景与挑…...

LLM - 在服务器中使用 Ollama + OpenWebUI 部署最新大模型
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/140992533 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 Ollama 是一个开源的大型语言模型(LLM)服务工具,目的是简化本地运行…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
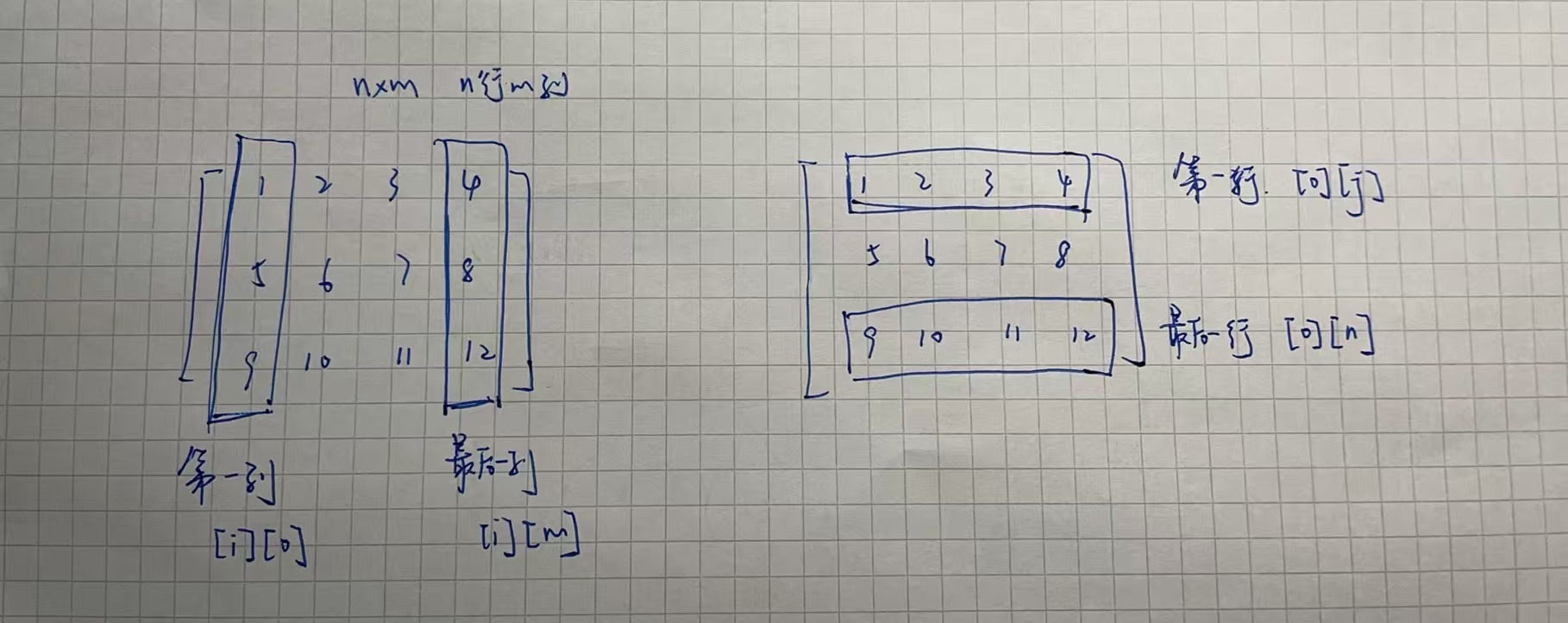
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

