「数组」归并排序 / if语句优化|小区间插入优化(C++)
概述
在上一篇文章中,我们介绍了快速排序以及随机快速排序:
「数组」快速排序 / 随机值优化|小区间插入优化(C++)
今天,我们来介绍归并排序。
相比于快速排序是冒泡排序融合了分治思想后形成的究极promax进化版,归并排序不来自任何一种使用分治的基础排序:它本人就是纯粹的分治。
思路
冯·诺依曼想过这么一个事:两个有序数组二路合并成一个有序数组的时间复杂度是线性的:
i 0 1 2 3 4
arr1[i] 1 5 6 8 9
arr2[i] 0 2 3 4 7ans[i] 1 2 3 4 5 6 7 8 9很明显, 你只需要双指针i和j分别指向两个数组,k指针指向答案数组,
每次都进行ans[k++]=min(arr1[i],arr2[j]),之后i++或j++(这要看min函数取到了谁)
就能在线性时间内得到合并好的数组。
那如果能把一个无序数组在中间一分为二成两个有序的子数组然后合并就好了,但是子数组怎么能有序呢?
那如果能把这两个子数组分成四个有序子数组然后合并就好了。
那如果能把这四个子数组分成八个有序子数组然后合并就好了。
.....................
那如果能把这一个数分成,诶,等等,一个数本来就有序啊。
那从这里再一层一层合并上去不就好了?冯·诺依曼恍然大悟。
算法过程
来把我们的思路实现一遍。
merge_sort()
我们给出函数merge_sort,它接收一个范围,它只干两件事:
①申请一个辅助数组。
②启动这个层层划分的过程。
让我们谈谈辅助数组:
在二路归并时,我们需要一个地方承载我们的结果。那不如就让原数组承载我们的结果,辅助数组[l,r)位置上拷贝一份原数组[l,r)位置上的值,两个指针i和j都指向辅助数组的对应位置,然后向原数组填入对应的结果。这样我们的排序结果就还放在原来的内存地址上。
void merge_sort(int arr[], int l, int r) {int* assist= new int[r-l];recursion(arr, l, r, assist);delete[] assist;
}recursion()
我们给出递归函数recursion,它只干两件事:
①一刀劈开接收到的数组,然后传给两个子recursion。
②在劈开的两个数组有序后启动二路合并。
*注意*:根据代码语言传统,l和r往往是一个左闭右开区间,即[l,r),表示范围取到l,但取不到r。两个子数组的范围分别是[l,m),[m,r)。
void recursion(int arr[], int l, int r, int assist[]) {if (r - l <= 1)return;int m = (l + r) / 2;recursion(arr, l, m, assist);recursion(arr, m, r, assist);merge(arr, l, m, r, assist);
}merge()
我们给出递归函数recursion,它只干两件事:
①把原数组对应位置的数据拷贝给辅助数组的对应位置。
②进行一个极其简单的二路合并。
*注意*:i或j触底后将另一个数组的剩余部分通通接入合并后数组的末尾。
void merge(int arr[], int l, int m, int r, int assist[]) {memcpy(&assist[l], &arr[l], sizeof(int) * (r - l));int i, j, k;for (i = l, j = m, k = l;; k++) {if (i == m || j == r)break;if (assist[i] <= assist[j])arr[k] = assist[i++];else arr[k] = assist[j++];}while (i != m)arr[k++] = assist[i++];while (j != r)arr[k++] = assist[j++];
}Code
void merge(int arr[], int l, int m, int r, int assist[]) {memcpy(&assist[l], &arr[l], sizeof(int) * (r - l));int i, j, k;for (i = l, j = m, k = l;; k++) {if (i == m || j == r)break;if (assist[i] <= assist[j])arr[k] = assist[i++];else arr[k] = assist[j++];}while (i != m)arr[k++] = assist[i++];while (j != r)arr[k++] = assist[j++];
}
void recursion(int arr[], int l, int r, int assist[]) {if (r - l <= 1)return;int m = (l + r) / 2;recursion(arr, l, m, assist);recursion(arr, m, r, assist);merge(arr, l, m, r, assist);
}
void merge_sort(int arr[], int l, int r) {int* assist= new int[r-l];recursion(arr, l, r, assist);delete[] assist;
}谈谈奇数
常有人对于归并排序对于奇数长度数组的可行性产生质疑。我们来思考一下这个问题。
先想想二路归并:
i 0 1 2 3 4
arr1[i] 1 5 6 8
arr2[i] 0 2 3 4 7ans[i] 1 2 3 4 5 6 7 8结合上面的merge()实现代码,你能发现:两个长度不同的子数组丝毫不影响二路归并的进行。
那么奇数数组导致的中间位置不均匀丝毫不会影响整个排序。
优化方案
1.if语句优化
在一些时候,二路合并根本没必要发生:第一个有序子数组的最后一个数比第二个有序子数组的第一个数小,那么他们天然就接在了一起。
void merge_if(int arr[], int l, int m, int r, int assist[]) {if (arr[m - 1] <= arr[m])return;memcpy(&assist[l], &arr[l], sizeof(int) * (r - l));int i, j, k;for (i = l, j = m, k = l;; k++) {if (i == m || j == r)break;if (assist[i] <= assist[j])arr[k] = assist[i++];else arr[k] = assist[j++];}while (i != m)arr[k++] = assist[i++];while (j != r)arr[k++] = assist[j++];
}2.小区间插入优化
最底层会产生大量recursion递归来对小区间二分,而他们分区的范围却极小,这是不必要的,而且相当被动。
插入排序在小区间的表现要好于快速分区,当分区小到某个程度时,我们直接转发给插入排序。
void recursion_with_insertion(int arr[], int l, int r, int assist[]) {if (r - l <= 20){insertion_sort(&arr[l], r - l); return;}int m = (l + r) / 2;recursion_with_insertion(arr, l, m, assist);recursion_with_insertion(arr, m, r, assist);merge_if(arr, l, m, r, assist);
}Code
void merge_if(int arr[], int l, int m, int r, int assist[]) {if (arr[m - 1] <= arr[m])return;memcpy(&assist[l], &arr[l], sizeof(int) * (r - l));int i, j, k;for (i = l, j = m, k = l;; k++) {if (i == m || j == r)break;if (assist[i] <= assist[j])arr[k] = assist[i++];else arr[k] = assist[j++];}while (i != m)arr[k++] = assist[i++];while (j != r)arr[k++] = assist[j++];
}
void recursion_with_insertion(int arr[], int l, int r, int assist[]) {if (r - l <= 20){insertion_sort(&arr[l], r - l); return;}int m = (l + r) / 2;recursion_with_insertion(arr, l, m, assist);recursion_with_insertion(arr, m, r, assist);merge_if(arr, l, m, r, assist);
}
void MGsort(int arr[], int l, int r) {int* assist = new int[r - l];recursion(arr, l, r, assist);delete[] assist;
}复杂度
时间复杂度:O(nlogn)
空间复杂度:O(n)
复杂度分析:
时间分析:
把一个长度为n的数组一直二分成长度为1的数组的次数是logn次,也就是有logn层
--------------------------------------
----------------- --------------------
--------- ------- ------ -------------
--- ----- --- -- -- --- --- ---------
- - - --- - - -- -- - - - - ---- ----
- - - - - - - - - - - - - - - - - - --
——————————————————n———————————————————
—m——m——m——m——m——m——m——m——m——m——m——m——m每一层都要对子数组两两二路合并,复杂度为O(m),m为子数组的长度 ,而每一层的全体m求和为n,故每一层的复杂度都为O(n),有logn层,故得到O(nlogn)。
空间分析:
使用了长度为n的辅助数组,故为O(n)。
*注意*:同一层的每次合并函数和递归函数结束后空间都会被释放,下次函数都会再次占据这块空间,空间复用使得每一层的复杂度都是O(1),函数的空间占用整体为O(logn) 。O(n+logn)=O(n)。
总结
分而治之,是为分治。
如果你的朋友问什么是分治,那么就给他讲讲归并排序。作为应用分治思想的算法,它真的纯粹到毫无保留。
相关文章:
)
「数组」归并排序 / if语句优化|小区间插入优化(C++)
概述 在上一篇文章中,我们介绍了快速排序以及随机快速排序: 「数组」快速排序 / 随机值优化|小区间插入优化(C) 今天,我们来介绍归并排序。 相比于快速排序是冒泡排序融合了分治思想后形成的究极promax进化版&…...
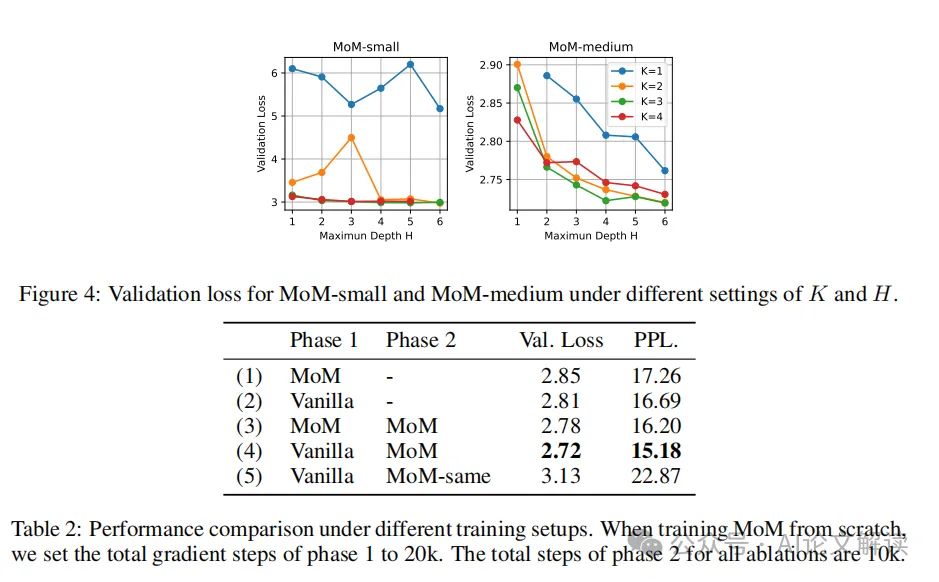
颠覆传统 北大新型MoM架构挑战Transformer模型,显著提升计算效率
挑战传统的Transformer模型设计 在深度学习和自然语言处理领域,Transformer模型已经成为一种标准的架构,广泛应用于各种任务中。传统的Transformer模型依赖于一个固定的、按深度排序的层次结构,每一层的输出都作为下一层的输入。这种设计虽然…...

接口优化笔记
索引 添加索引 where条件的关键自动或者order by后面的排序字段可以添加索引加速查询 索引只能通过删除新增进行修改,无法直接修改。 # 查看表的索引 show index from table_name; show create table table_name; # 添加索引 alter table table_name add index …...

pandas 科学计数法显示
我注意到pandas中有一个问题, 默认情况下,就是其中的数据的小数位不能超过6位,比如0.0000007就会被显示为0,这个结果如下 全部以科学技术显示 import pandas as pd import numpy as np# 设置显示格式为科学计数法 pd.options.d…...

PHP正则替换字符串中的图片地址
在PHP中,可以使用preg_replace()函数来实现正则表达式的替换功能。以下是一个简单的例子,演示如何替换字符串中的图片地址。 double $str 图片地址1:<img src"http://example.com/image1.jpg"> 图片地址2:<i…...

基于多商户AI智能名片商城小程序的粉丝忠诚度提升策略:深度融合足额法则与多维度激励体系
摘要:在数字化浪潮的推动下,多商户AI智能名片商城小程序以其独特的商业模式和技术优势,正逐步成为连接商家与消费者,特别是粉丝群体的重要平台。本文深入探讨了如何通过深度融合足额法则与多维度激励体系,有效提升多商…...

BigDecimal高精度运算
1. BigDecimal是什么类型,为什么可以转为double BigDecimal 是 Java 中用于表示任意精度的十进制数的类。它主要用于金融和商业计算,能够提供比 double 类型更高精度的运算,特别是在处理货币等需要精确计算的场景中。 1.1 BigDecimal 的基…...

C/C++实现蓝屏2.0
🚀欢迎互三👉:程序猿方梓燚 💎💎 🚀关注博主,后期持续更新系列文章 🚀如果有错误感谢请大家批评指出,及时修改 🚀感谢大家点赞👍收藏⭐评论✍ 前…...

Unity音频管理器插件AudioToolKit
Unity音频管理器插件AudioToolKit 介绍AudioToolKit介绍具体用法总结 介绍 最近在自己写音频管理器的时候在网上发现了一款比较好用并且功能很全的一个音频管理插件,叫做AudioToolKit的插件。 如果需要的可以直接从我资源中找AudioToolKit。 AudioToolKit介绍 A…...
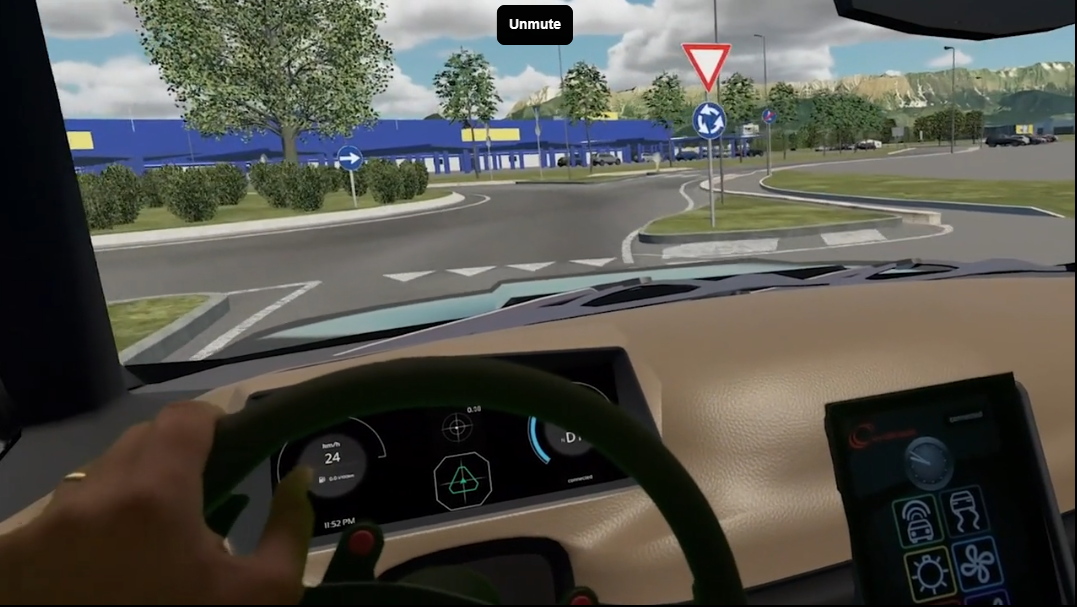
搜维尔科技:驾驶模拟器背后的技术: Varjo的虚拟/混合现实 (VR/XR)提供独特的优势,最终加快汽车开发创新的步伐
专业驾驶模拟器广泛应用于车辆开发,帮助汽车行业在开发过程的早期做出更好的设计决策。总体目标是为测试驾驶员提供最真实的驾驶体验,包括动态动作和声音,并测试控制算法或辅助系统等功能。环境越真实,驾驶员的体验就越接近最终车…...

OSL 冠名赞助Web3峰会 “FORESIGHT2024”圆满收官
OSL 望为香港数字资产市场发展建设添砖加瓦 (香港,2024 年 8 月 13 日)- 8 月 11 日至 12 日, 由 香港唯一专注数字资产的上市公司 OSL 集团(863.HK)冠名赞助,Foresight News、 Foresight Ventu…...

LeetCode 3148.矩阵中的最大得分:每个元素与其左或上元素之差的最大值(原地修改O(1)空间)
【LetMeFly】3148.矩阵中的最大得分:每个元素与其左或上元素之差的最大值(原地修改O(1)空间) 力扣题目链接:https://leetcode.cn/problems/maximum-difference-score-in-a-grid/ 给你一个由 正整数 组成、大小为 m x n 的矩阵 g…...

主流的开源大型语言模型
本期我们来聊聊目前主流的开源大型语言模型。这些模型就像是AI界的超级英雄,各具特色,为我们的研究和开发提供了强大的力量。🚀 GPT-Neo:这是EleutherAI的杰作,它模仿了OpenAI的GPT-3。GPT-Neo虽然规模小一些…...

【自动驾驶】话题通信
目录 构建发布者构建订阅者编写lanch文件自动启动节点测试运行ROS的目录结构 切换到工作空间的src目录下: 构建发布者 catkin_create_pkg publisher std_msgs rospy roscpp编写发布者程序: // 1.包含头文件 #include "ros/ros.h" #include &…...

【Linux】中的软件安装:深入探索RPM、SRPM与YUM
🐇明明跟你说过:个人主页 🏅个人专栏:《Linux :从菜鸟到飞鸟的逆袭》🏅 🔖行路有良友,便是天堂🔖 目录 一、引言 1、Linux的起源与发展 2、RPM、SRPM与YUM的简要介…...

uniapp自定义请求头信息header
添加请求头:uniapp自定义请求头信息header,如下:添加tenant-id参数 代码...
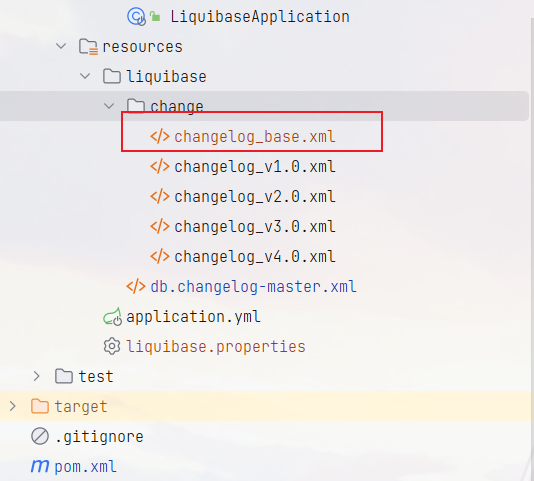
SpringBoot整合Liquibase
1、是什么? Liquibase官网 Liquibase是一个开源的数据库管理工具,可以帮助开发人员管理和跟踪数据库变更。它可以与各种关系型数据库和NoSQL数据库一起使用,并提供多种数据库任务自动化功能,例如数据库迁移、版本控制和监控。Li…...

虚幻5|给武器添加碰撞检测与伤害
本章内容衔接上两章,需要完成上两章才能用本章内容 虚幻5|角色武器装备的数据库学习(不只是用来装备武器,甚至是角色切换也很可能用到)-CSDN博客虚幻5|普通攻击,使用接口更方便-CSDN博客 如有疑问,可访问…...

RESTful API设计指南:构建高效、可扩展的Web服务
目录 引言 一.RESTful API概述 二.设计原则 2.1. 资源导向 2.2. 使用标准的HTTP方法 2.3. 无状态通信 2.4. 可缓存响应 2.5. 分层系统 2.6. 按需加载代码(可选) 2.7. HATEOAS 三.最佳实践 3.1. 明确资源和子资源 3.2. 使用合适的HTTP状态码 …...

黑马头条vue2.0项目实战(九)——编辑用户资料
目录 1. 创建组件并配置路由 2. 页面布局 3. 展示用户信息 4. 修改昵称 5. 修改性别 6. 修改生日 7. 修改头像 7.1 图片上传预览 7.2 使用纯客户端的方式处理用户头像上传预览 7.3 头像裁切 7.4 纯客户端的图片裁切上传流程 7.5 Cropper.js 图片裁剪器的基本使用 …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
