机器学习 第11章-特征选择与稀疏学习
机器学习 第11章-特征选择与稀疏学习
11.1 子集搜索与评价
我们将属性称为“特征”(feature),对当前学习任务有用的属性称为“相关特征”(relevant feature)、没什么用的属性称为“无关特征”(irrelevant feature)。从给定的特征集合中选择出相关特征子集的过程,称为“特征选择”(feature selection)。
特征选择是一个重要的“数据预处理”(data preprocessing)过程,在现实机器学习任务中,获得数据之后通常先进行特征选择,此后再训练学习器。
特征选择过程必须确保不丢失重要特征,否则后续学习过程会因为重要信息的缺失而无法获得好的性能。给定数据集,若学习任务不同,则相关特征很可能不同,因此,特征选择中所谓的“无关特征”是指与当前学习任务无关。有一类特征称为“冗余特征”(redundant feature),它们所包含的信息能从其他特征中推演出来。
冗余特征在很多时候不起作用,去除它们会减轻学习过程的负担。但有时冗余特征会降低学习任务的难度,例如若学习目标是估算立方体的体积,则“底面积”这个冗余特征的存在将使得体积的估算更容易;更确切地说,若某个冗余特征恰好对应了完成学习任务所需的“中间概念”,则该冗余特征是有益的。
对于子集搜索问题,有三种基于贪心的策略:
前向搜索:将每个特征当做一个候选子集,然后从当前所有的候选子集中选择出最佳的特征子集;接着在上一轮选出的特征子集中添加一个新的特征,同样地选出最佳特征子集;最后直至选不出比上一轮更好的特征子集。
后向搜索:类似于前向搜索,但是每次是去掉一个无关特征。
双向搜索:把前向和后向结合,每次增加相关特征,去除无关特征。
对于子集评价问题,给定数据集 D D D,假定 D D D中第 i i i类样本所占的比例为 p i ( i = 1 , 2 , . . . , ∣ Y ∣ ) p_i(i=1,2,...,|Y|) pi(i=1,2,...,∣Y∣)。为便于讨论,假定样本属性均为离散型。对属性子集 A A A,假定根据其取值将 D D D分成了 V V V个子集 { D 1 , D 2 , . . . , D V } \{D^1,D^2,...,D^V\} {D1,D2,...,DV},每个子集中的样本在 A A A上取值相同,于是我们可计算属性子集 A A A 的信息增益
G a i n ( A ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(A)=Ent(D)-∑^V_{v=1}{|D^v|\over |D|}Ent(D^v) Gain(A)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
其中信息熵定义为
E n t ( D ) = − ∑ i = 1 ∣ Y ∣ p k l o g 2 p k Ent(D)=-∑^{|Y|}_{i=1}p_klog_2p_k Ent(D)=−i=1∑∣Y∣pklog2pk
信息增益 G a i n ( A ) Gain(A) Gain(A)越大,意味着特征子集 A A A包含的有助于分类的信息越多。于是,对每个候选特征子集,我们可基于训练数据集 D D D来计算其信息增益,以此作为评价准则。
将特征子集搜索机制与子集评价机制相结合,即可得到特征选择方法。
常见的特征选择方法大致可分为三类:过滤式(6lter)、包裹式(wrapper)和嵌入式(embedding)。
11.2 过滤式选择
过滤式方法先对数据集进行特征选择,然后再训练学习器,特征选择过程与后续学习器无关。
Relief(Relevant Features)是一种著名的过滤式特征选择方法,该方法设计了一个“相关统计量”来度量特征的重要性。该统计量是一个向量,其每个分量分别对应于一个初始特征,而特征子集的重要性则是由子集中每个特征所对应的相关统计量分量之和来决定。
显然,Relief的关键是如何确定相关统计量。给定训练集 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … 。, ( x m , y m ) } \{(x_1,y_1),(x_2,y_2),…。,(x_m,y_m)\} {(x1,y1),(x2,y2),…。,(xm,ym)},对每个示例 x i x_i xi,Relief先在 x i x_i xi的同类样本中寻找其最近邻 x i , n h x_{i,nh} xi,nh,称为“猜中近邻”(near-hit),再从KaTeX parse error: Expected group after '_' at position 2: x_̲的异类样本中寻找其最近邻 x i , n m x_{i,nm} xi,nm,称为“猜错近邻”(near-miss),然后,相关统计量对应于属性j的分量为
δ j = ∑ i − d i f f ( x i j , x i , n h j ) 2 + d i f f ( x i j , x i , n m j ) 2 \delta ^j=\sum_{i}-diff(x_i^j,x_{i,nh}^j)^2+diff(x_i^j,x_{i,nm}^j)^2 δj=i∑−diff(xij,xi,nhj)2+diff(xij,xi,nmj)2
Relief是为二分类问题设计的,其扩展变体Relief-F能处理多分类问题。假定数据集 D D D中的样本来自 ∣ Y ∣ |Y| ∣Y∣个类别。对示例KaTeX parse error: Expected group after '_' at position 2: x_̲,若它属于第 k k k类 ( k ∈ { 1 , 2 , . . . , ∣ Y ∣ } (k∈\{1,2,...,|Y|\} (k∈{1,2,...,∣Y∣},则Relief-F先在第 k k k类的样本中寻找 x i x_i xi的最近邻示例 x i , n h x_{i,nh} xi,nh并将其作为猜中近邻,然后在第 k k k类之外的每个类中找到一个 x i x_i xi的最近邻示例作为猜错近邻,记为 x i , n m x_{i,nm} xi,nm ( l = 1 , 2 , . … , ∣ Y ∣ ; l ≠ k ) (l=1,2,.…,|Y|;l≠k) (l=1,2,.…,∣Y∣;l=k)。于是,相关统计量对应于属性 j j j的分量为
δ j = ∑ i − d i f f ( x i j , x i , n h j ) 2 + ∑ l ≠ k ( p l ∗ d i f f ( x i j , x i , n m j ) 2 ) \delta ^j=\sum_{i}-diff(x_i^j,x_{i,nh}^j)^2+\sum_{l\neq k}(p_l*diff(x_i^j,x_{i,nm}^j)^2) δj=i∑−diff(xij,xi,nhj)2+l=k∑(pl∗diff(xij,xi,nmj)2)
11.3 包裹式选择
与过滤式特征选择不考虑后续学习器不同,包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价准则。换言之,包裹式特征选择的目的就是为给定学习器选择最有利于其性能、“量身定做”的特征子集
一般而言,由于包裹式特征选择方法直接针对给定学习器进行优化,因此从最终学习器性能来看,包裹式特征选择比过滤式特征选择更好,但另一方面由于在特征选择过程中需多次训练学习器,因此包裹式特征选择的计算开销通常比过滤式特征选择大得多。
LVW是一种典型的包裹式特征选择方法。其在拉斯维加斯框架下使用随即策略来进行自己搜索,并以最终分类器的误差为特征子集的评价准则。其算法描述如下图所示:

需注意的是,由于 LVW 算法中特征子集搜索采用了随机策略,而每次特征子集评价都需训练学习器,计算开销很大,因此算法设置了停止条件控制参数T。然而,整个 LVW 算法是基于拉斯维加斯方法框架,若初始特征数很多(即4|很大)、T设置较大,则算法可能运行很长时间都达不到停止条件。换言之若有运行时间限制,则有可能给不出解。
11.4 嵌入式选择与 L 1 L_1 L1正则化
在过滤式和包裹式特征选择方法中,特征选择过程与学习器训练过程有明显的分别;与此不同,嵌入式特征选择是将特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择。
给定数据集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x m , y m ) D={(x_1,y_1),(x_2,y_2),⋯,(x_m,y_m)} D=(x1,y1),(x2,y2),⋯,(xm,ym),其中 x ∈ R d , y ∈ R x∈R^d,y∈R x∈Rd,y∈R, 我们考虑最简单的线性回归模型,以平方误差为损失函数,则优化目标为
m i n w ∑ i = 1 m ( y i − w T x i ) 2 min_w∑^m_{i=1}(yi−w^Txi)^2 minwi=1∑m(yi−wTxi)2
当样本特征很多,而样本数相对较少时,很容易陷入过拟合。为了缓解过拟合问题,可对引入正则化项。若使用 L 2 L_2 L2范数正则化,则有
m i n w ∑ i = 1 m ( y i − w T x i ) 2 + λ ∣ ∣ w ∣ ∣ 2 2 min_w∑^m_{i=1}(yi−w^Tx_i)^2+λ||w||^2_2 minwi=1∑m(yi−wTxi)2+λ∣∣w∣∣22
可以使用别的 L p L_p Lp范数来替代原本的 L 2 L_2 L2范数,如 L 1 L_1 L1范数。那么可以得到:
m i n w ∑ i = 1 m ( y i − w T x i ) 2 + λ ∥ w ∥ 1 min_w∑^m_{i=1}(yi−w^Tx_i)^2+λ∥w∥_1 minwi=1∑m(yi−wTxi)2+λ∥w∥1
该式称为LASSO。
11.5 稀疏表示与字典学习
不妨把数据集 D考虑成一个矩阵,其每行对应于一个样本,每列对应于一个特征。特征选择所考虑的问题是特征具有“稀疏性”,即矩阵中的许多列与当前学习任务无关,通过特征选择去除这些列,则学习器训练过程仅需在较小的矩阵上进行,学习任务的难度可能有所降低,涉及的计算和存储开销会减少学得模型的可解释性也会提高
现在我们来考虑另一种稀疏性:D所对应的矩阵中存在很多零元素,但这些零元素并不是以整列、整行形式存在的。
若给定一个稠密矩阵,我们能通过某种方法找到其合适的稀疏表示,可以使得学习任务更加简单高效,我们称之为稀疏编码或字典学习。
给定一个数据集,字典学习最简单的形式为:
m i n B , α i ∑ i = 1 m ∥ x i − B α i ∥ 2 2 + λ ∑ i = 1 m ∥ α i ∥ 1 min_{B,αi}∑^m_{i=1}∥x_i−Bα_i∥^2_2+λ∑^m_{i=1}∥α_i∥_1 minB,αii=1∑m∥xi−Bαi∥22+λi=1∑m∥αi∥1
11.6 压缩感知
在现实任务中,我们常希望根据部分信息来恢复全部信息。例如在数据通讯中要将模拟信号转换为数字信号,根据奈奎斯特(Nyquist)采样定理,令采样频率达到模拟信号最高频率的两倍,则采样后的数字信号就保留了模拟信号的全部信息;换言之,由此获得的数字信号能精确重构原模拟信号。然而,为了便于传输、存储,在实践中人们通常对采样的数字信号进行压缩,这有可能损失一些信息,而在信号传输过程中,由于信道出现丢包等问题,又可能损失部分信息。那么,接收方基于收到的信号,能否精确地重构出原信号呢?压缩感知(compressed sensing)为解决此类问题提供了新的思路。
与特征选择、稀疏表示不同,压缩感知关注的是如何利用信号本身所具有的稀疏性,从部分观测样本中恢复原信号。通常认为,压缩感知分为“感知测量”和“重构恢复”这两个阶段。“感知测量”关注如何对原始信号进行处理以获得稀疏样本表示,这方面的内容涉及傅里叶变换、小波变换以及 11.5节介绍的字典学习、稀疏编码等,不少技术在压缩感知提出之前就已在信号处理等领域有很多研究:“重构恢复”关注的是如何基于稀疏性从少量观测中恢复原信号,这是压缩感知的精髓,当我们谈到压缩感知时,通常是指该部分。
相关文章:

机器学习 第11章-特征选择与稀疏学习
机器学习 第11章-特征选择与稀疏学习 11.1 子集搜索与评价 我们将属性称为“特征”(feature),对当前学习任务有用的属性称为“相关特征”(relevant feature)、没什么用的属性称为“无关特征”(irrelevant feature)。从给定的特征集合中选择出相关特征子集的过程&a…...
Grok 2携AI图片生成重生
埃隆马斯克(Elon Musk)的人工智能初创公司xAI推出其最新的AI助手Grok 2的测试版,添加了类似于OpenAI的DALL-E和Google的Gemini的图像生成工具,但对可以生成的图像类型的限制显然较少。<这是其中的一个“亮点”,一些…...
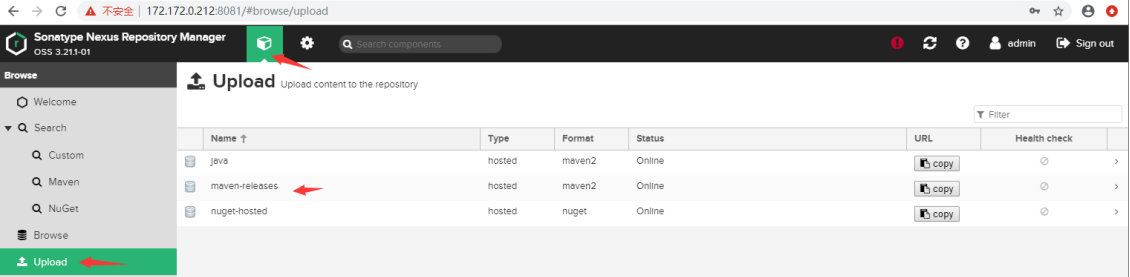
使用Nexus搭建Maven私服仓库
一、私服仓库简介 在Java的世界中,我们通常使用Maven的依赖体系来管理构件(artifact,又称为二方库或三方库)的依赖,Maven仓库用于存储这些构件。一般的远程仓库(比如Maven Central)只提供下载功…...

云计算day27
任务背景 公司的服务器越来越多, 维护⼀些简单的事情都会变得很繁琐。⽤ shell脚本来管理少量服务器效率还⾏, 服务器多了之后, shell脚本⽆ 法实现⾼效率运维。这种情况下,我们需要引⼊⾃动化运维⼯具, 对 多台服务器实现⾼效运维。 任务要求任务要求 通过管…...

关于HTTP HEAD介绍
一、HTTP HEAD介绍 HTTP HEAD 是一种 HTTP 请求方法,它用于请求服务器返回指定资源的元信息(metadata),而不包括响应体的内容。这种请求方式常用于客户端预先评估资源的大小、最后修改日期或其他头信息,而无需实际下载…...
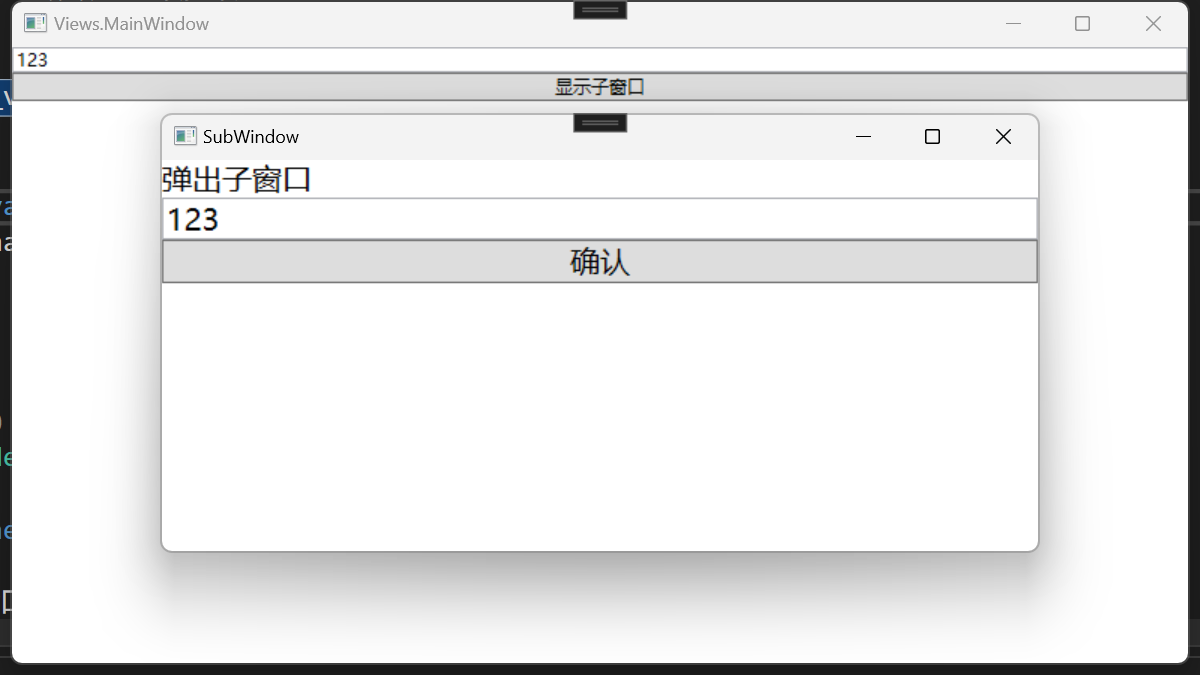
WPF Mvvm
了解MVVM 什么是MVVM:一种设计模式 设计模式(Design pattern)代表了最佳的实践,通常被有经验的面向对象的软件开发人员所采用。设计模式是软件开发人员在软件开发过程中面临的一般问题的解决方案。这些解决方案是众多软件开发人…...

pnpm【实用教程】2024最新版
pnpm 简介 pnpm 全称 performant npm,即高性能的 npm,由 npm/yarn 衍生而来,解决了 npm/yarn 内部潜在的 bug,极大的优化了性能,扩展了使用场景,被誉为 最先进的包管理工具 安装 pnpm npm i -g pnpm使用 pn…...

C#的前沿技术有哪些?
C#作为.NET平台的核心语言,其前沿技术主要围绕.NET生态系统的扩展和更新展开。了解C#的前沿技术对于开发者来说至关重要,因为它们代表了该语言和平台的最新发展方向和趋势。目前,C#的前沿技术主要集中在以下几个方面: 1. NET 6: …...
Vue2移动端(H5项目)项目基于vant封装图片上传组件(支持批量上传、单个上传、回显、删除、预览、最大上传数等功能)---解决批量上传问题
一、最终效果 二、参数配置 1、代码示例: <t-uploadfileList"fileList":showFileList"showFileList"showFile"showFile":showFileUrl"showFileUrl"/>2、配置参数(TUpload Attributes)继承va…...

ELK整合实战,filebeat和logstash采集SpringBoot项目日志发送至ES
文章目录 ELK整合实战使用FileBeats将日志发送到Logstash配置Logstash接收FileBeat收集的数据并打印Logstash输出数据到Elasticsearch利用Logstash过滤器解析日志Grok插件Grok语法用法 输出到Elasticsearch指定索引 前文:FileBeats详解 前文:logstash详解…...

网络编程:OSI协议,TCP/IP协议,IP地址,UDP编程
目录 国际网络通信协议标准: 1.OSI协议: 2.TCP/IP协议模型: 应用层 : 传输层: 网络层: IPV4协议 IP地址 IP地址的划分: 公有地址 私有地址 MA…...

QtExa001自动包装流水线的框架设计vs2019QT
QtExa001自动包装流水线的框架设计 工程代码: https://download.csdn.net/download/txwtech/89636815https://download.csdn.net/download/txwtech/89636815 主界面: 设置:进行参数配置,保存ini文件 调试:tcp/ip&…...

SpringBoot拦截器的使用介绍
SpringBoot拦截器的使用介绍 本篇文章主要讲的是 SpringBoot 拦截器的使用介绍。 1、定义拦截器 拦截器:所谓拦截器,就是能够在进行某个操作之前拦截请求,如果请求符合条件就允许在往下执行。 定义拦截器的几种方式。 1.1 实现HandleInt…...

Spring Boot应用中的资源分离与高效打包实践
在电商网站项目中,前端资源通常包括HTML、CSS、JavaScript、图片、字体等静态文件,以及Thymeleaf或Freemarker等模板引擎渲染的页面。将这些资源从Spring Boot主应用中分离出来,不仅有利于前后端团队的并行开发,还能提高应用的加载…...

分析 avformat_open_input 数据读取过程
------------------------------------------------------------ author: hjjdebug date: 2024年 08月 13日 星期二 17:31:43 CST descriptor: 分析 avformat_open_input 数据读取过程 ------------------------------------------------------------ avformat_open_input 中读…...
 VS Data Integration (通常被称为 Kettle))
Apache HOP (Hop Orchestration Platform) VS Data Integration (通常被称为 Kettle)
Apache HOP (Hop Orchestration Platform) 和 Data Integration (通常被称为 Kettle) 都是强大的 ETL (Extract, Transform, Load) 工具, 它们都由 Hitachi Vantara 开发和支持。尽管它们有着相似的目标,即帮助用户进行数据集成任务,但它们在…...

如何判断一个dll/exe是32位还是64位
通过记事本判断(可判断C或者C#) 64位、将dll用记事本打开,可以看到一堆乱码,但是找到乱码行的第一个PE,如果后面是d?则为64位 32位、将dll用记事本打开,可以看到一堆乱码,但是找到乱码行的第…...

加速网页加载,提升用户体验:HTML、JS 和 Vue 项目优化全攻略
在信息爆炸的时代,网页加载速度成为了用户体验的重中之重。试想一下,如果一个页面加载超过 3 秒,你还有耐心等待吗? 为了留住用户,提升转化率,网页优化势在必行! 本文将从 HTML、JavaScript 和…...

LVS服务器基础环境配置
环境配置 1 基础服务关闭 setenforce 0 # 临时关闭selinuxvi /etc/sysconfig/selinux # 永久关闭selinuxsystemctl disable --now firewalld # 关闭防火墙systemctl disable --now NetworkManager # 关闭网络管理器2 centos7软件仓库的配置 mount /dev/cdrom /media以防万一&…...

【Python OpenCV】使用OpenCV实现两张图片拼接
问题引入: 如何使用Python OpenCV实现两张图片的水平拼接和垂直拼接 代码实现: import cv2 import numpy as npdef image_hstack(image_path_1, image_path_2):"""两张图片左右拼接"""img1 cv2.imread(image_path_1)img…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
