JS(三)——更改html内数据
- 获取 DOM 元素,然后修改其属性或内容。使用
getElementById方法获取特定 ID 的元素:
<p id="myParagraph">这是初始的文本</p>const paragraph = document.getElementById('myParagraph');
paragraph.innerHTML = '这是修改后的文本';- 通过修改元素的属性,比如修改
img元素的src属性:
<img id="myImage" src="old.jpg" />const image = document.getElementById('myImage');
image.src = 'new.jpg';使用 getElementsByTagName 或 getElementsByClassName 方法获取一组元素进行修改
<p class="myClass">第一段</p>
<p class="myClass">第二段</p>const paragraphs = document.getElementsByClassName('myClass');
for (let i = 0; i < paragraphs.length; i++) {paragraphs[i].innerHTML = '修改后的段落';
}相关文章:
——更改html内数据)
JS(三)——更改html内数据
获取 DOM 元素,然后修改其属性或内容。使用 getElementById 方法获取特定 ID 的元素: <p id"myParagraph">这是初始的文本</p> const paragraph document.getElementById(myParagraph); paragraph.innerHTML 这是修改后的文本…...

CSS小玩意儿:文字适配背景
一,效果 二,代码 1,搭个框架 添加一张背景图片,在图片中显示一行文字。 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" conte…...
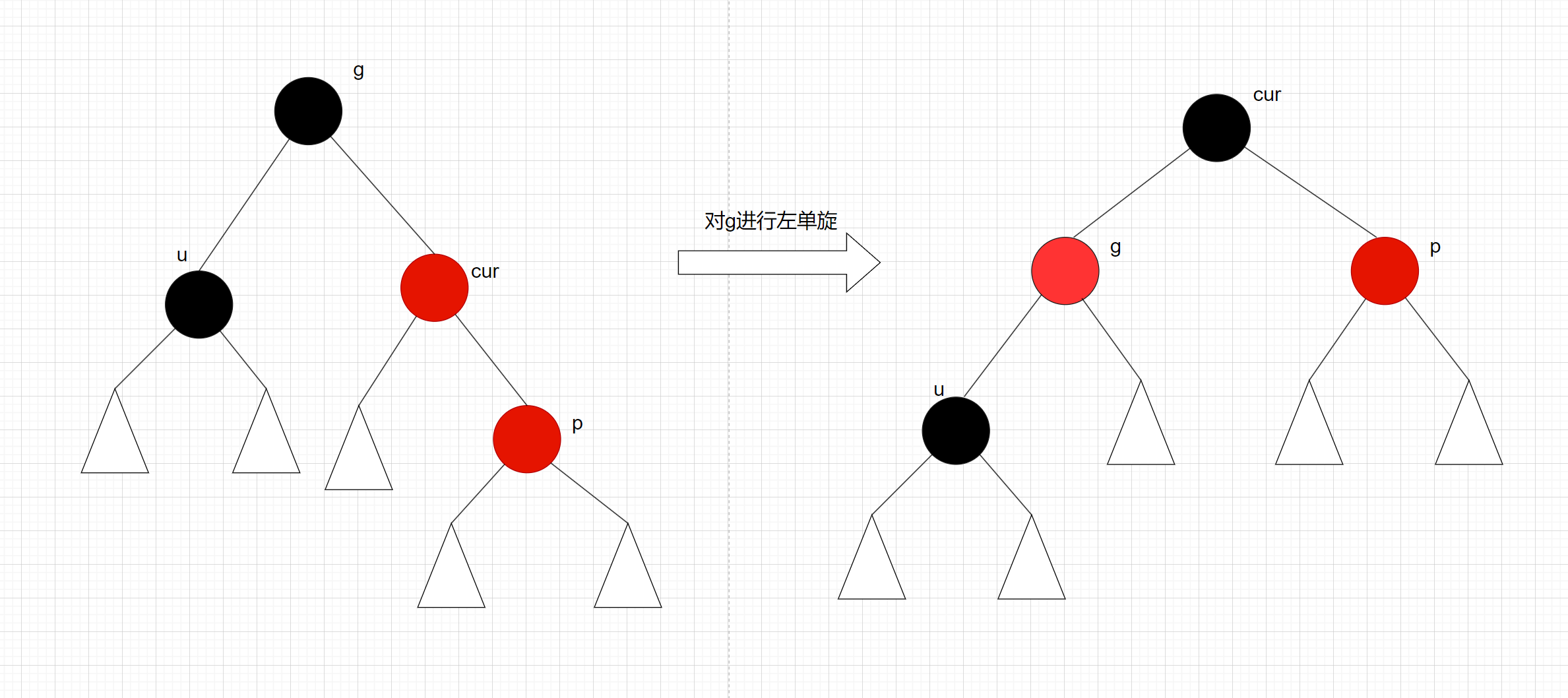
C++:平衡二叉搜索树之红黑树
一、红黑树的概念 红黑树, 和AVL都是二叉搜索树, 红黑树通过在每个节点上增加一个储存位表示节点的颜色, 可以是RED或者BLACK, 通过任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树能够确保没有一条路径会比…...

CentOS 7 系统优化
CentOS 7 系统优化 1、配置YUM源 阿里云的YUM源配置: CentOS 7使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repoCentOS 8使用以下命令: sudo wget -O /etc/yum.repos.d/CentOS…...

扫雷游戏——附源代码
扫雷游戏的源代码比较简单,不设计比较复杂的代码,主要是多个函数的组合,每个函数执行自己的功能,最终支持游戏的完成。 1.菜单 我们需要一个提醒信息来让用户进行选择。 void menu() {printf("***********************\n&…...
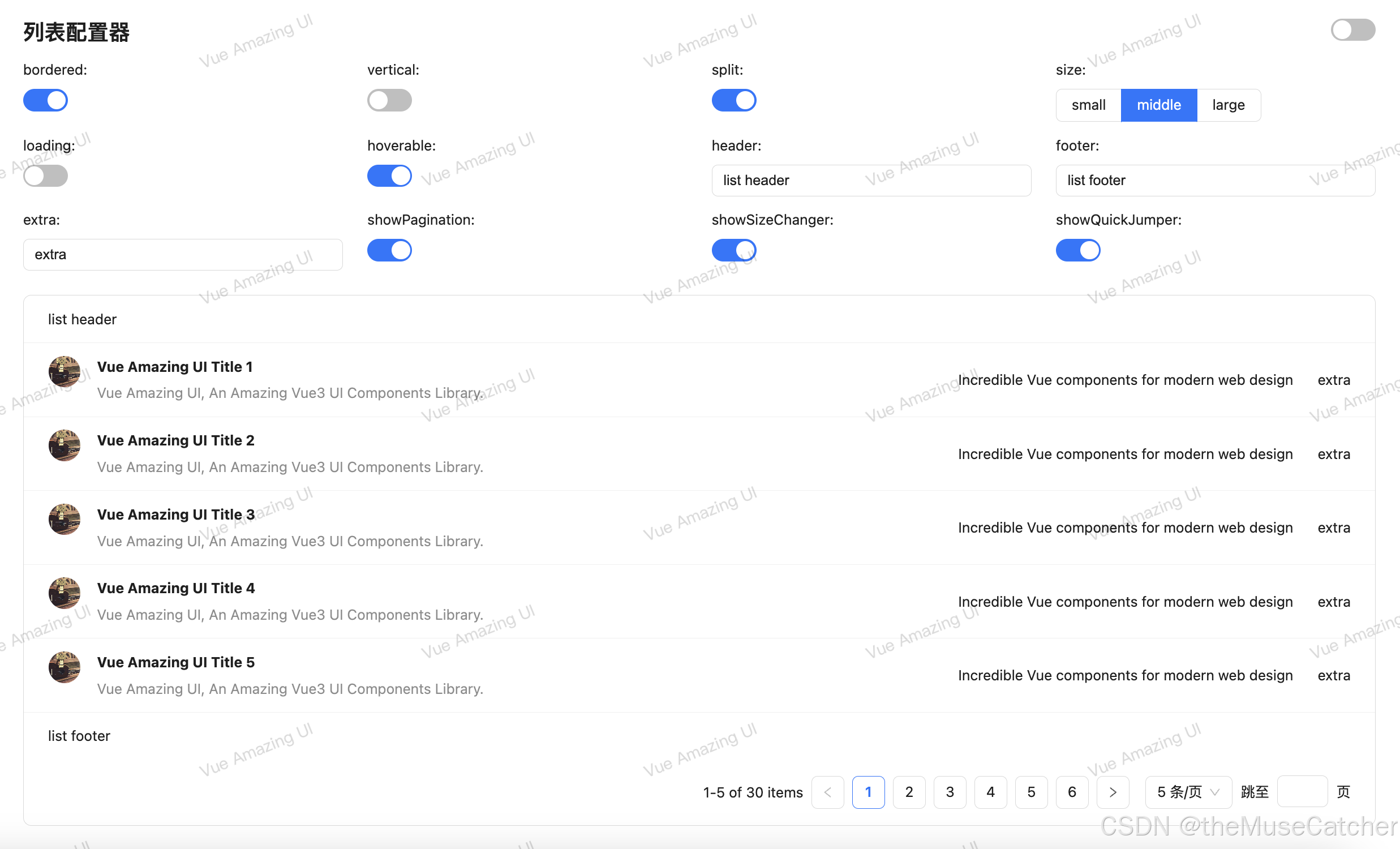
Vue3列表(List)
效果如下图:在线预览 APIs List 参数说明类型默认值bordered是否展示边框booleanfalsevertical是否使用竖直样式booleanfalsesplit是否展示分割线booleantruesize列表尺寸‘small’ | ‘middle’ | ‘large’‘middle’loading是否加载中booleanfalsehoverable是否…...

HarmonyOS NEXT - Navigation组件封装BaseNavigation
demo 地址: https://github.com/iotjin/JhHarmonyDemo 代码不定时更新,请前往github查看最新代码 在demo中这些组件和工具类都通过module实现了,具体可以参考HarmonyOS NEXT - 通过 module 模块化引用公共组件和utils 官方介绍 组件导航 (Navigation)(推…...
浅看MySQL数据库
有这么一句话:“一个不会数据库的程序员不是合格的程序员”。有点夸张,但是确是如此。透彻学习数据库是要学习好多知识,需要学的东西也是偏难的。我们今天来看数据库MySQL的一些简单基础东西,跟着小编一起来看一下吧。 什么是数据…...
)
Pytorch常用训练套路框架(CPU)
文章目录 1. 数据准备示例:加载 CIFAR-10 数据集 2. 模型定义示例:定义一个简单的卷积神经网络 3. 损失函数和优化器示例:定义损失函数和优化器 4. 训练循环示例:训练循环 5. 评估和测试示例:评估模型 6. 保存和加载模…...

C++ | Leetcode C++题解之第338题比特位计数
题目: 题解: class Solution { public:vector<int> countBits(int n) {vector<int> bits(n 1);for (int i 1; i < n; i) {bits[i] bits[i & (i - 1)] 1;}return bits;} };...
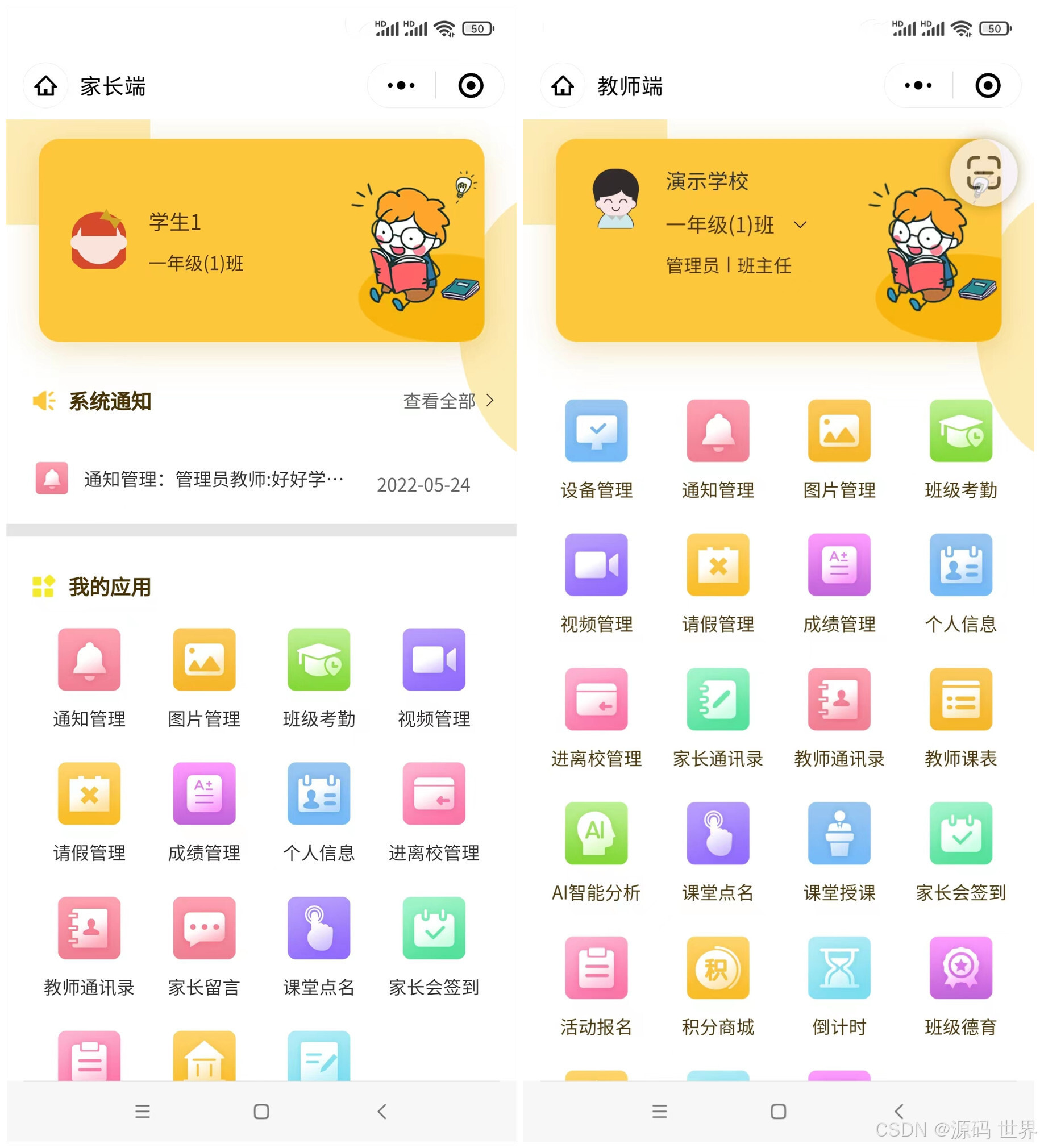
智慧校园云平台电子班牌系统源码,智慧教育一体化云解决方案
智慧校园云平台电子班牌系统,利用先进的云计算技术,将教育信息化资源和教学管理系统进行有效整合,实现生态基础数据共享、应用生态统一管理,为智慧教育建设的统一性,稳定性,可扩展性,互通性提供…...

数据库系统 第17节 数据仓库 案例赏析
下面我将通过几个具体的案例来说明数据仓库如何在不同的行业中发挥作用,并解决实际业务问题。 案例 1: 零售业 背景: 一家大型零售商希望改进其库存管理和市场营销策略,以提高销售额和顾客满意度。 解决方案: 数据仓库: 构建一个数据仓库࿰…...
硬件面试经典 100 题(71~90 题)
71、请问下图电路的作用是什么? 该电路实现 IIC 信号的电平转换(3.3V 和 5V 电平转换),并且是双向通信的。 上下两路是一样的,只分析 SDA 一路: 1) 从左到右通信(SDA2 为输入状态&…...

【git】代理相关
问题: 开启了翻墙代理工具,拉取代码时报错:fatal: 无法访问 xxxx : Failed to connect to github.com port 443: 连接超时 解决: 0,取消代理仍然无法拉取 1,查看控制面板-网络与Internet-代理ÿ…...
方式和闭包函数方式定义gin中间件)
golang gin框架中创建自定义中间件的2种方式总结 - func(*gin.Context)方式和闭包函数方式定义gin中间件
在gin框架中,我们可以通过2种方式创建自定义中间件: 1. 直接定义一个类型为 func(*gin.Context)的函数或者方法 这种方式是我们常用的方式,也就是定义一个参数为*gin.Context的函数或者方法。定义的方法就是创建一个 参数类型为 gin.Handler…...

Linux高级编程 8.13 文件IO
一、文件IO 操作系统为了方便用户使用系统功能而对外提供的一组系统函数。称之为 系统调用(unistd.h) 其中有个 文件IO,一般都是对设备文件操作,当然也可以对普通文件进行操作。 这是一个基于Linux内核的没有缓存的IO机制 文件IO特性&…...

【k8s】ubuntu18.04 containerd 手动从1.7.15 换为1.7.20
ubutnu18.04之前手动安装了1.7.15现在下载1.7.20containerd-1.7.20-linux-amd64.tar.gz root@k8s-worker-i58265u:/home/zhangbin# root@k8s-worker-i58265u:/home/zhangbin# https://github.com/containerd/containerd/releases/download/v1.7.20/containerd-1.7.20-linux-am…...

常用浮动方式
目录 一、标准流 二、float浮动 三、 flex浮动 3.1flex组成 3.2 主轴对齐方式 3.3侧轴对齐方式 3.4修改主轴方向 3.5弹性盒子换行 3.6行对齐方式 一、标准流 标签在网页中的默认排布规则 例如: 块元素独占一行、行内元素可以一行显示多个 二、float浮动 让块…...

设计模式反模式:UML常见误用案例分析
文章目录 设计模式反模式:UML常见误用案例分析1. 反模式概述2. 反模式的 UML 图示误用2.1 God Object 反模式2.2 Spaghetti Code 反模式2.3 Golden Hammer 反模式2.4 Poltergeist 反模式 3. 总结 设计模式反模式:UML常见误用案例分析 在软件工程领域&am…...

Python编码系列—Python SQL与NoSQL数据库交互:深入探索与实战应用
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
