【贪心算法】一文让你学会“贪心”(贪心算法详解及经典案例)
文章目录
- 前言
- 如何理解“贪心算法”?
- 贪心算法实战分析
- 1.分糖果
- 2.钱币找零
- 3.区间覆盖
- 内容小结
- 最后说一句

🐱🐉作者简介:大家好,我是黑洞晓威,一名大二学生,希望和大家一起进步。
👿本文收录于 算法,本专栏是针对大学生、初学算法的人准备,解析常见的数据结构与算法,同时备战蓝桥杯。
前言
贪心算法是一种非常常见的算法,它的简单和高效性使其在实际应用中被广泛使用。
贪心算法的核心思想是在每一步都采取当前状态下最优的选择,而不考虑未来可能产生的影响。虽然贪心算法不能保证总是得到最优解,但在很多情况下,它可以获得很好的结果。
本篇文章将介绍贪心算法的基本概念和一些经典应用,以及如何通过贪心算法来解决一些实际问题。希望通过本文的阅读,读者可以对贪心算法有更加深刻的理解,并能够在实际问题中应用贪心算法来得到更好的解决方案。
让我们暴打贪心算法吧!

如何理解“贪心算法”?
关于贪心算法,我们先看一个例子。
假设我们有一个可以容纳100kg物品的背包,可以装各种物品。我们有以下5种豆子,每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大,我们如何选择在背包中装哪些豆子?每种豆子又该装多少呢?

实际上,这个问题很简单,我估计你一下子就能想出来,没错,我们只要先算一算每个物品的单价,按照单价由高到低依次来装就好了。单价从高到低排列,依次是:黑豆、绿豆、红豆、青豆、黄豆,所以,我们可以往背包里装20kg黑豆、30kg绿豆、50kg红豆。
这个问题的解决思路显而易见,它本质上借助的就是贪心算法。结合这个例子,我总结一下贪心算法解决问题的步骤,我们一起来看看。
第一步,当我们看到这类问题的时候,首先要联想到贪心算法:针对一组数据,我们定义了限制值和期望值,希望从中选出几个数据,在满足限制值的情况下,期望值最大。
类比到刚刚的例子,限制值就是重量不能超过100kg,期望值就是物品的总价值。这组数据就是5种豆子。我们从中选出一部分,满足重量不超过100kg,并且总价值最大。
第二步,我们尝试看下这个问题是否可以用贪心算法解决:每次选择当前情况下,在对限制值同等贡献量的情况下,对期望值贡献最大的数据。
类比到刚刚的例子,我们每次都从剩下的豆子里面,选择单价最高的,也就是重量相同的情况下,对价值贡献最大的豆子。
第三步,我们举几个例子看下贪心算法产生的结果是否是最优的。大部分情况下,举几个例子验证一下就可以了。严格地证明贪心算法的正确性,是非常复杂的,需要涉及比较多的数学推理。而且,从实践的角度来说,大部分能用贪心算法解决的问题,贪心算法的正确性都是显而易见的,也不需要严格的数学推导证明。
实际上,用贪心算法解决问题的思路,并不总能给出最优解。
我来举一个例子。在一个有权图中,我们从顶点S开始,找一条到顶点T的最短路径(路径中边的权值和最小)。贪心算法的解决思路是,每次都选择一条跟当前顶点相连的权最小的边,直到找到顶点T。按照这种思路,我们求出的最短路径是S->A->E->T,路径长度是1+4+4=9。

但是,这种贪心的选择方式,最终求的路径并不是最短路径,因为路径S->B->D->T才是最短路径,因为这条路径的长度是2+2+2=6。为什么贪心算法在这个问题上不工作了呢?
在这个问题上,贪心算法不工作的主要原因是,前面的选择,会影响后面的选择。如果我们第一步从顶点S走到顶点A,那接下来面对的顶点和边,跟第一步从顶点S走到顶点B,是完全不同的。所以,即便我们第一步选择最优的走法(边最短),但有可能因为这一步选择,导致后面每一步的选择都很糟糕,最终也就无缘全局最优解了。
贪心算法实战分析
对于贪心算法,你是不是还有点懵?如果死抠理论的话,确实很难理解透彻。掌握贪心算法的关键是多练习。只要多练习几道题,自然就有感觉了。所以,我带着你分析几个具体的例子,帮助你深入理解贪心算法。
1.分糖果
我们有m个糖果和n个孩子。我们现在要把糖果分给这些孩子吃,但是糖果少,孩子多(m<n),所以糖果只能分配给一部分孩子。
每个糖果的大小不等,这m个糖果的大小分别是s1,s2,s3,……,sm。除此之外,每个孩子对糖果大小的需求也是不一样的,只有糖果的大小大于等于孩子的对糖果大小的需求的时候,孩子才得到满足。假设这n个孩子对糖果大小的需求分别是g1,g2,g3,……,gn。
我的问题是,如何分配糖果,能尽可能满足最多数量的孩子?
我们可以把这个问题抽象成,从n个孩子中,抽取一部分孩子分配糖果,让满足的孩子的个数(期望值)是最大的。这个问题的限制值就是糖果个数m。
我们现在来看看如何用贪心算法来解决。对于一个孩子来说,如果小的糖果可以满足,我们就没必要用更大的糖果,这样更大的就可以留给其他对糖果大小需求更大的孩子。另一方面,对糖果大小需求小的孩子更容易被满足,所以,我们可以从需求小的孩子开始分配糖果。因为满足一个需求大的孩子跟满足一个需求小的孩子,对我们期望值的贡献是一样的。
我们每次从剩下的孩子中,找出对糖果大小需求最小的,然后发给他剩下的糖果中能满足他的最小的糖果,这样得到的分配方案,也就是满足的孩子个数最多的方案。
2.钱币找零
这个问题在我们的日常生活中更加普遍。假设我们有1元、2元、5元、10元、20元、50元、100元这些面额的纸币,它们的张数分别是c1、c2、c5、c10、c20、c50、c100。我们现在要用这些钱来支付K元,最少要用多少张纸币呢?
在生活中,我们肯定是先用面值最大的来支付,如果不够,就继续用更小一点面值的,以此类推,最后剩下的用1元来补齐。
在贡献相同期望值(纸币数目)的情况下,我们希望多贡献点金额,这样就可以让纸币数更少,这就是一种贪心算法的解决思路。直觉告诉我们,这种处理方法就是最好的。实际上,要严谨地证明这种贪心算法的正确性,需要比较复杂的、有技巧的数学推导,我不建议你花太多时间在上面,不过如果感兴趣的话,可以自己去研究下。
3.区间覆盖
假设我们有n个区间,区间的起始端点和结束端点分别是[l1, r1],[l2, r2],[l3, r3],……,[ln, rn]。我们从这n个区间中选出一部分区间,这部分区间满足两两不相交(端点相交的情况不算相交),最多能选出多少个区间呢?

这个问题的处理思路稍微不是那么好懂,不过,我建议你最好能弄懂,因为这个处理思想在很多贪心算法问题中都有用到,比如任务调度、教师排课等等问题。
这个问题的解决思路是这样的:我们假设这n个区间中最左端点是lmin,最右端点是rmax。这个问题就相当于,我们选择几个不相交的区间,从左到右将[lmin, rmax]覆盖上。我们按照起始端点从小到大的顺序对这n个区间排序。
我们每次选择的时候,左端点跟前面的已经覆盖的区间不重合的,右端点又尽量小的,这样可以让剩下的未覆盖区间尽可能的大,就可以放置更多的区间。这实际上就是一种贪心的选择方法。

内容小结
今天我们学习了贪心算法。
实际上,贪心算法适用的场景比较有限。这种算法思想更多的是指导设计基础算法。比如最小生成树算法、单源最短路径算法,这些算法都用到了贪心算法。 从我个人的学习经验来讲,不要刻意去记忆贪心算法的原理,多练习才是最有效的学习方法。
贪心算法的最难的一块是如何将要解决的问题抽象成贪心算法模型,只要这一步搞定之后,贪心算法的编码一般都很简单。贪心算法解决问题的正确性虽然很多时候都看起来是显而易见的,但是要严谨地证明算法能够得到最优解,并不是件容易的事。所以,很多时候,我们只需要多举几个例子,看一下贪心算法的解决方案是否真的能得到最优解就可以了。
最后说一句
感谢大家的阅读,文章通过网络资源与自己的学习过程整理出来,希望能帮助到大家。
才疏学浅,难免会有纰漏,如果你发现了错误的地方,可以提出来,我会对其加以修改。

相关文章:

【贪心算法】一文让你学会“贪心”(贪心算法详解及经典案例)
文章目录前言如何理解“贪心算法”?贪心算法实战分析1.分糖果2.钱币找零3.区间覆盖内容小结最后说一句🐱🐉作者简介:大家好,我是黑洞晓威,一名大二学生,希望和大家一起进步。 👿本…...
【字体图标iconfont】字体图标部署流程+项目源码分析
今日,心情甚是烦闷,原由… 公司项目需要将字体图标做一些细微的调整,我一人分析了许久,看不大懂源码的逻辑,产生了自我怀疑。深吸一口气,重新鼓起勇气,调整心境,一下子豁然开朗&…...

2023最全的Web自动化测试介绍(建议收藏)
做测试的同学们都了解,做Web自动化,我们主要用Selenium或者是QTP。 有的人可能就会说,我没这个Java基础,没有Selenium基础,能行吗?测试虽然属于计算机行业,但其实并不需要太深入的编程知识&…...
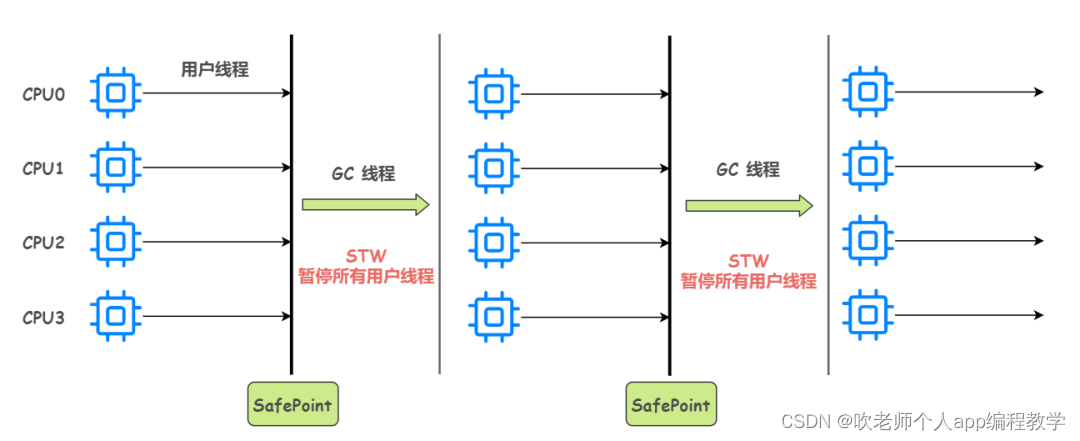
jvm_根节点枚举安全点安全区域
1、可达性分析可以分成两个阶段 根节点枚举 从根节点开始遍历对象图 前文我们在介绍垃圾收集算法的时候,简单提到过:标记-整理算法(Mark-Compact)中的移动存活对象操作是一种极为负重的操作,必须全程暂停用户应用程序才能进行,像这…...

fabric(token-erc-20链码部署)
确保自己已经安装了fabric。没有安装的可以参考我之前的教程fabric中bootstrap.sh到底帮助我们干了什么?(手动执行相关操作安装fabric2.4)_./bootstrap.sh_小小小小关同学的博客-CSDN博客小伙伴们在跟着官方示例来安装fabric的时候都是相当烦…...
C语言基础——流程控制语句
文章目录一、流程控制语句 -- 控制程序的运行过程 9条(一)、条件选择流程控制语句:if语句if……else……语句if……else if……语句switch语句(二)、循环流程控制语句:for语句while语句do while……语句co…...

WinForm | C# 界面弹出消息通知栏 (仿Win10系统通知栏)
ApeForms 弹出消息通知栏功能 文章目录ApeForms 弹出消息通知栏功能前言全局API通知栏起始方向通知排列方向通知栏之间的间隔距离无鼠标悬停时的不透明度消息通知窗体的默认大小示例代码文本消息提示栏文本消息提示栏(带选项)图文消息提示栏图文消息提示…...

刷题之最长公共/上升子序列问题
目录 一、最长公共子序列问题(LCS) 1、题目 2、题目解读 编辑 3、代码 四、多写一题 五、应用 二、最长上升子序列问题(LIS) 1、题目 2、题目解读 3、代码 四、多写一道 Ⅰ、题目解读 Ⅱ、代码 一、最长公共子序列问题&…...

【数据结构】千字深入浅出讲解栈(附原码 | 超详解)
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石. 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:C语言实现数据结构 💬总结:希望你看完…...

自动驾驶V2X
1 SoC MDM9250 2 设备网络节点 mhi_swip0 rmnet_mhi0 3 网络协议栈log打印控制 include/linux/netdevice.h ethtool -s eth0 msglvl [level] ethtool -s eth0 msglvl 0x6001 4 URLs MHI initial design review https://lore.kernel.org/lkml/001601d52148$bd852840$388f78c0$c…...

零基础自学网络安全/渗透测试有哪些常见误区?
一、网络安全学习的误区 1.不要试图以编程为基础去学习网络安全 不要以编程为基础再开始学习网络安全,一般来说,学习编程不但学习周期长,且过渡到网络安全用到编程的用到的编程的关键点不多。一般人如果想要把编程学好再开始学习网络安全往…...
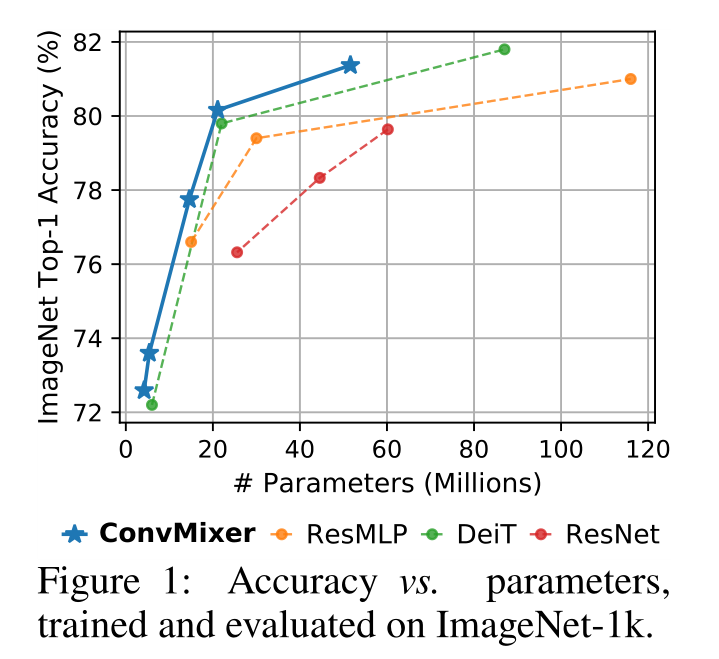
ConvMixer:Patches Are All You Need
Patches Are All You Need 发表时间:[Submitted on 24 Jan 2022]; 发表期刊/会议:Computer Vision and Pattern Recognition; 论文地址:https://arxiv.org/abs/2201.09792; 代码地址:https:…...

day10—编程题
文章目录1.第一题1.1题目1.2思路1.3解题2.第二题2.1题目2.2涉及的相关知识2.3思路2.4解题1.第一题 1.1题目 描述: 给定一个二维数组board,代表棋盘,其中元素为1的代表是当前玩家的棋子,0表示没有棋子,-1代表是对方玩…...
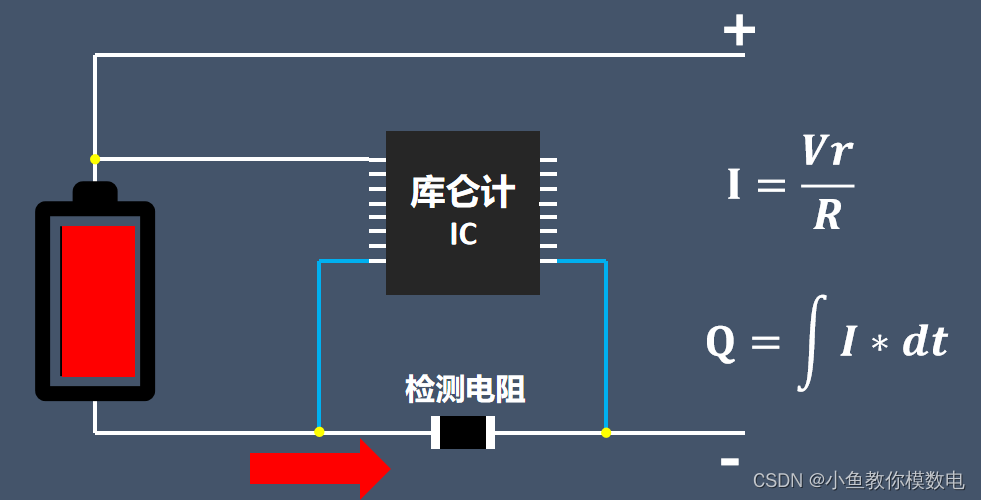
如何测量锂电池的电量
锂电池在放电时我们有时需要知道电池的实时电量,如电池电量低了我们就需要及时给锂电池充电,避免电池过度放电。我手里的这个就是个单节锂电池电量显示模块,只需要将这个模块接到锂电池的正负极即可显示电量。这个模块的电量分为四档…...

菜鸟刷题Day6
⭐作者:别动我的饭 ⭐专栏:菜鸟刷题 ⭐标语:悟已往之不谏,知来者之可追 一.链表内指定区间反转:链表内指定区间反转_牛客题霸_牛客网 (nowcoder.com) 描述 将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转…...

DecimalFormat格式化显示数字
DecimalFormat 是 NumberFormat 的一个具体子类,用于格式化十进制数字,可以实现以最快的速度将数字格式化为你需要的样子。 DecimalFormat 类主要靠 # 和 0 两种占位符号来指定数字长度。0 表示如果位数不足则以 0 填充, # 表示只要有可能就…...

cpu中缓存简介
一级缓存是什么: 一级缓存都内置在CPU内部并与CPU同速运行,可以有效的提高CPU的运行效率。一级缓存越大,CPU的运行效率越高,但受到CPU内部结构的限制,一级缓存的容量都很小。 CPU缓存(Cache Memory…...
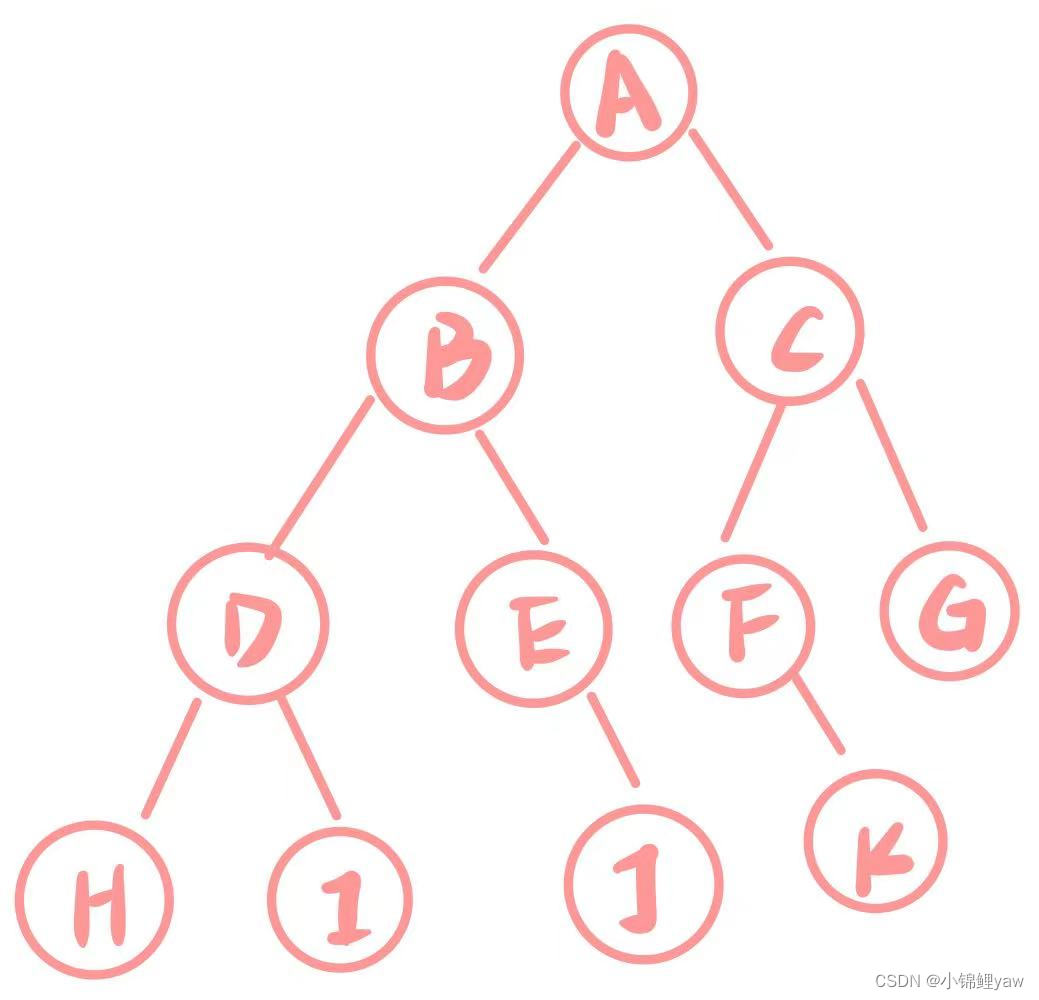
【数据结构】二叉树的遍历以及基本操作
目录 1.树形结构 1.概念 2.二叉树 2.1概念 2.2 两种特殊的二叉树 2.3二叉树的存储 2.4二叉树的基本操作 1.手动快速创建一棵简单的二叉树 2.二叉树的遍历 (递归) 3.二叉树的层序遍历 4.获取树中节点的个数 5.获取叶子节点的个数 6.获取第K层节点的个数 7.获取二叉…...
若依框架 --- ruoyi 表格的设置
表格 字典值转换 (1) 方式1:使用字典枚举的方式 var isDownload [[${dict.getType(YES_OR_NO)}]];{field : isDownload,title : 是否允许下载,formatter: function(value, row, index) {return $.table.selectDictLabel(isDownload, value);} }, (2) 方式2&…...

“两会”网络安全相关建议提案回顾
作为新一年的政治、经济、社会等发展的“风向标”,今年“两会”在3月13日顺利闭幕。在今年“两会”期间,多位人大代表也纷纷围绕网络安全、数据安全的未来发展做了提案和建议。 01 “两会”网络安全相关建议和提案回顾 建议统筹智能网联汽车数据收集与共…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
