【数据结构】二叉树的遍历以及基本操作

目录

1.树形结构

1.概念

2.二叉树

2.1概念

2.2 两种特殊的二叉树

2.3二叉树的存储

2.4二叉树的基本操作

1.手动快速创建一棵简单的二叉树

2.二叉树的遍历 (递归)

3.二叉树的层序遍历

4.获取树中节点的个数

5.获取叶子节点的个数

6.获取第K层节点的个数

7.获取二叉树的高度

8.检测值为value的元素是否存在

9.判断一棵树是不是完全二叉树

---

        

1.树形结构

1.概念

        树是一种非线性的数据结构

        有一个特殊的结点，称为根结点，根结点没有前驱结点

        每棵子树的根结点有且只有一个前驱，可以有0个或多个后继

        树是递归定义的

注意：树形结构中，子树之间不能有交集，否则就不是树形结构

结点的度：当前节点子树的个数；

树的度：最大的结点的度；

叶子结点或终端结点：度为0的结点称为叶结点

父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；

子结点：一个结点含有的子树的根结点称为该结点的子结点；

根结点：没有前驱的结点

结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推

树的高度或深度：树中结点的最大层次；

2.二叉树

2.1概念

1. 二叉树不存在度大于2的结点

2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

2.2 两种特殊的二叉树

1. 满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵 二叉树的层数为K，且结点总数是 2^k - 1，则它就是满二叉树。

2. 完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n 个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树

2.3二叉树的存储

二叉树的存储结构分为：顺序存储和类似于链表的链式存储。

二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式，具体如下

// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}

2.4二叉树的基本操作

1.手动快速创建一棵简单的二叉树

 

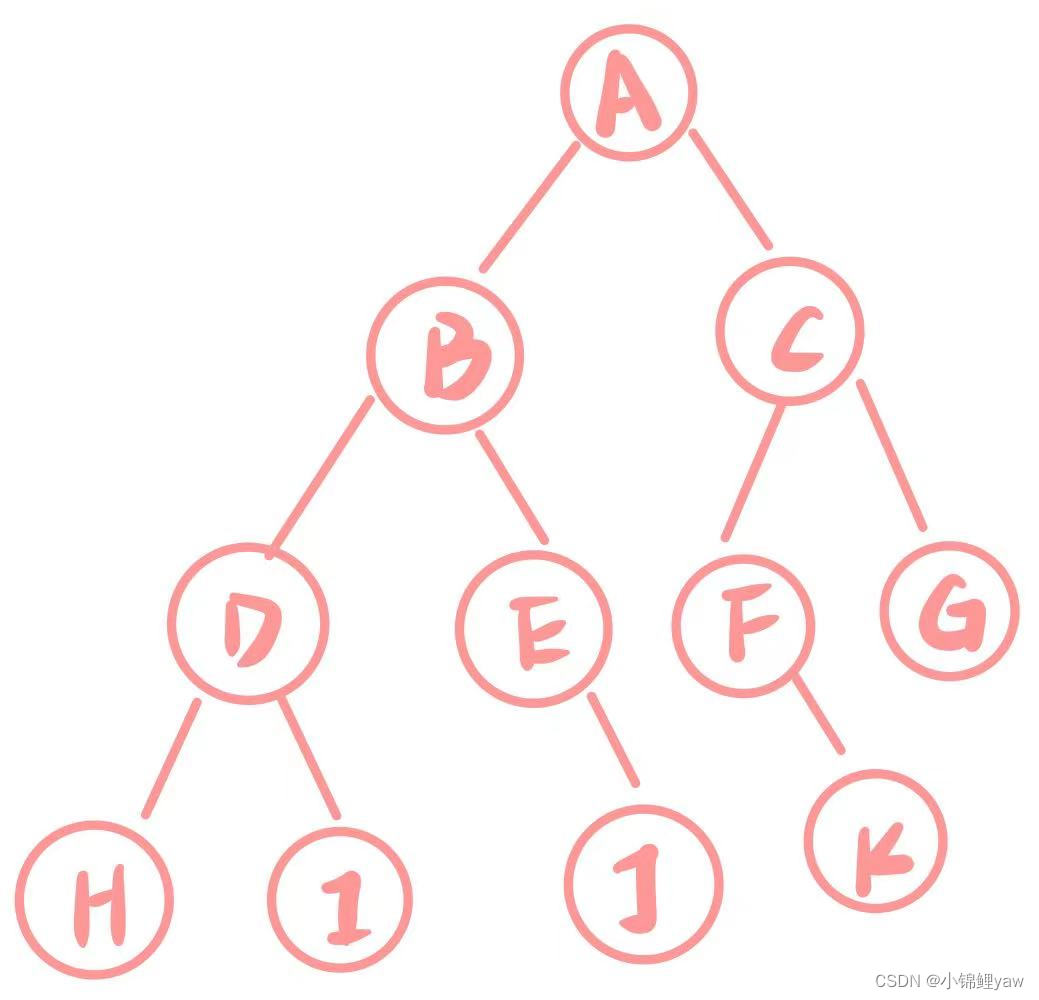
public Node TreeBuild(){Node node1 = new Node('A');Node node2 = new Node('B');Node node3 = new Node('C');Node node4 = new Node('D');Node node5 = new Node('E');Node node6 = new Node('F');Node node7 = new Node('G');Node node8 = new Node('H');Node node9 = new Node('I');Node node10 = new Node('J');Node node11 = new Node('K');node1.left = node2;node1.right = node3;node2.left = node4;node2.right = node5;node3.left = node6;node3.right = node7;node4.left = node8;node4.right = node9;node5.right = node10;node6.right = node11;return node1;}

2.二叉树的遍历 (递归)

·   //前序遍历public void preOrder(Node root){if(root == null){return ;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}//中序遍历public void inOrder(Node root){if(root == null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}//后序遍历public void postOrder(Node root){if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}

3.二叉树的层序遍历

    //层序遍历public List<List<Character>> levelOrder(Node root){//创建一个二维数组保存每一层的元素List<List<Character>> list = new ArrayList<>();if(root == null){return list;}//临时队列Deque<Node> deque = new LinkedList<>();//头节点放入队列deque.offer(root);//队列非空进循环while(!deque.isEmpty()){int size = deque.size();List<Character> curList = new ArrayList<>();for (int i = 0; i < size; i++){Node x = deque.pop();//左子树不为空，左子树入队列if(x.left != null){deque.offer(x.left);}//右子树不为空，右子树入队列if(x.right != null){deque.offer(x.right);}//出栈的元素值存放在临时数组里curList.add(x.val);}//出循环将临时数组加入二维数组list.add(curList);}return list;}

4.获取树中节点的个数

    public int size(Node root){if(root == null){return 0;}return 1 + size(root.left) + size(root.right);}

5.获取叶子节点的个数

    // 获取叶子节点的个数int getLeafNodeCount(Node root){if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}

6.获取第K层节点的个数

    // 获取第K层节点的个数int getKLevelNodeCount(Node root,int k){if(root == null || k <= 0){return 0;}if(k == 1){return 1;}return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);}

7.获取二叉树的高度

    // 获取二叉树的高度int getHeight(Node root){if(root == null){return 0;}return 1 + Math.max(getHeight(root.left),getHeight(root.right));}

8.检测值为value的元素是否存在

    // 检测值为value的元素是否存在public boolean find(Node root, int val){if(root == null){return false;}if(root.val == val){return true;}return find(root.left,val) || find(root.right,val);}

9.判断一棵树是不是完全二叉树

    // 判断一棵树是不是完全二叉树boolean isCompleteTree(Node root){if(root == null){return true;}//队列为空出循环，两个阶段//1.所有都是度为2的节点//2.碰到第一个度为1的节点，右节点直接false,左节点进入第二阶段//碰到第一个度为0的节点，进入第二阶段//3。第二阶段，都是叶子节点，如果有不是叶子节点，直接falseDeque<Node> deque = new LinkedList<>();deque.offer(root);boolean flag = true;while(!deque.isEmpty()){if(flag){Node x = deque.poll();if(x.left != null && x.right != null){deque.offer(x.left);deque.offer(x.right);}else if(x.right != null){return false;}else if(x.left != null){deque.offer(x.left);flag = false;}else {flag = false;}}else {Node x = deque.poll();if(x.left != null || x.right != null){return false;}}}return true;}