XCPC第十三站,贪心问题

一.区间选点

我们采取这样的策略来选点:step(1)将区间按照右端点的大小从小到大排序;step(2)从前往后依次枚举每个区间,如果当前区间中已经包含点,直接pass,否则选当前区间的右端点。因为右端点是最容易被下一个区间包含进去的,所以我们每次选择的都是当前情况下的局部最优解,这种策略就叫作贪心。
设最优解的点数是ans,按照算法找到的点数是cnt,下面我们证明ans == cnt。首先证明ans<=cnt。根据算法思路,这样选择以后每个区间都包含了点(否则会选右端点),因此算法得到一个可行解。又ans是所有可行解的最小值,因此ans<=cnt。再证明ans>=cnt。如果要执行选一个新的点的操作,那么后一个区间和前一个区间一定无交集。这样一来,我们就至少得到了cnt个互不相交的区间,每个这样的区间我们都选了它的右端点。要覆盖这些区间至少需要cnt个点,因此ans>=cnt。终上,ans == cnt。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int res;
struct range
{int l,r;bool operator< (const range W)const{return r<W.r;}
}range[N];
int main()
{int n;cin>>n;//要从0开始读入而不能从1开始读入,因为排序的是编号从0到(n-1)的数据,如果读到n的话会导致最后一个数据没有排序。//从小到大枚举每个区间for(int i = 0;i<n;i++){int a,b;cin>>a>>b;range[i] = {a,b};}sort(range,range+n);//ed表示枚举的上一个区间的右端点。初始时赋值为负无穷,这是因为第一次总是要加点的。int ed = -2e9;//要从0开始不能从1开始,理由同上for(int i = 0;i<n;i++){//上一个区间的右端点小于当前区间的左端点,说明两个区间没有交集,那么就要选一个新的点if(ed<range[i].l){res++;//更新右端点的值ed = range[i].r;}}cout<<res<<endl;
}
二.最大不相交区间数量

本题代码与上一题完全相同。下面我们来说明为什么按照上题策略选出的点数即为最大不相交区间数量。设ans为最大不相交区间数量,cnt为按照算法找出的区间数量。根据上题,根据算法选出的区间没有交集,因此是一个可行解。而ans是可行解的最大值,因此ans>=cnt。再证明ans<=cnt。采用反证法。假设ans>cnt,说明我们可以找到ans个互不相交的区间,要用点把这些区间覆盖至少需要ans>cnt个点。但是根据第一题,cnt个点已经可以把所有选出的区间覆盖,矛盾。终上,ans ==cnt。
三.区间分组

对于本题,我们的策略如下:step(1)将所有区间按照左端点从小到大排序;step(2)从前往后枚举所有区间,枚举当前已有的所有组,判断能否将该区间放进已有的某个组中(即判断某个是否有某个组的区间的右端点最大值小于当前区间的左端点,若<,可以放机;否则无法放进)。若可以放进某个组,就放进去并更新该组右端点的最大值;若不存在这样的组,就开一个新组把这个区间放进去。
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 100010;
struct range
{int l,r;//重载小于号bool operator<(const range W) const{return l<W.l;}
}range[N];
int main()
{int n;cin>>n;for(int i = 0;i<n;i++){int a,b;cin>>a>>b;range[i] = {a,b};}//将区间按照左端点从小到大排序sort(range,range+n);//堆里存储的是各个组的最大右端点priority_queue<int,vector<int>,greater<int> >heap;//从前往后扫描区间for(int i = 0;i<n;i++){//如果堆是空的或者堆的最小值(即所有最大右端点的最小值)仍然大于等于当前区间的左端点,说明不存在某个组,其内的区间与当前区间均无交集,这时候就要开一个新的组。if(heap.empty()||heap.top()>=range[i].l) heap.push(range[i].r);//否则这样的区间存在,放进这个组即可。为了平衡组数,要把堆顶弹出(否则算heap元素个数的时候会多算一个),并且让当前区间的右端点入堆,参与最小最右端点的“选拔”else if(heap.top()<range[i].l){//此时可以放进某个组,为了更新最右端点的最小值我们要把rangeheap.pop();heap.push(range[i].r);}}cout<<heap.size()<<endl;return 0;
}
下面我们证明根据这种策略得到的组数就是答案。记正确答案为ans,根据算法选出的答案是cnt,那么由于算法可以选出一种可行方案,ans<=cnt。而怎么证明ans>=cnt呢?我们考察最后一次开新组的时刻。

在该时刻,前cnt-1组的max_r都要比当前区间的l大(也就是要开新组的情形)。但是由于我们是按照左端点从小到大排序的,而该区间在最后才被放进去,因此它的l要大于前面所有max_r的区间的l,故它的l就是前面这些max_r属于的区间的一个交点。加上该区间本身,一共有cnt个区间,它们存在交集,因此必须把它们分开,因此ans>=cnt。终上,ans == cnt。
四.区间覆盖
我们采取这样的策略:step(1)将所有区间按照左端点从小到大排序;step(2)从前往后枚举每个区间,每次选择有可能覆盖左端点(start)的区间中右端点最靠右的区间(贪心的),再讲start更新成右端点的最大值。为什么按照这种策略得到的区间数目就是要求的答案呢?假设最佳方案选出的区间数是ans,算法选出的区间数是cnt。我们选择答案的区间组和算法的区间组的第一个不同的区间(假设是第二个),那么由于算法选择的是可能覆盖左端点的右端点最靠右的区间,因此有r1<=r2.又要不留缝隙,所以l1<=r1。所以l1<=r1<=r2。因此我们可以把上面的区间换成下面的区间。对其它不同的区间做类似操作,便可知道cnt == ans。

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int s,t,n,res;
struct range
{int l,r;//重载小于号bool operator < (const range W)const{return l<W.l;}
}range[N];
int main()
{cin>>s>>t>>n;for(int i = 0;i<n;i++){int a,b;cin>>a>>b;range[i].l = a;range[i].r = b;}//将区间按照左端点从小到大排序sort(range,range+n);bool flag = false;//双指针算法,依次处理每个区间for (int i = 0; i < n; i ++ ){//选择可能覆盖左端点的区间中右端点最靠右的区间int j = i, r = -2e9;while (j < n && range[j].l <= s){r = max(r, range[j].r);j ++ ;}
//如果所有可能覆盖左端点的区间中右端点最靠右的区间的右端点都够不到给定区间的左端点,说明无法覆盖if (r < s){res = -1;break;}
//否则能成功覆盖,所需的区间数加一res ++ ;//如果r>=t说明给定的区间已经被完全覆盖,不再需要执行循环,退出即可if (r >= t){flag = true;break;}
//更新s和i的值,进行下一轮s = r;i = j - 1; }if (!flag) res = -1;printf("%d\n", res);return 0;
}
五.排队打水
 假设第i个打水的人用时为ti,那么总的等待时间就应该是t1*(n-1)+t2*(n-2)+……+tn-1这里我们直接给出一种贪心的策略:按照用时的多少从小到大排队。下面我们证明这种方法的等待时间是最少的。下面假设t1<t2<……tn。假若最优解不是按照时间长短来依次打水,那么一定存在相邻的两个人(记为j和tj+1)满足tj>tj+1。现在我们将这两个人打水的顺序调换,不影响其他人的等待时间,但是我们减少了tj*(n-j)+tj+1*(n-j-1)-tj+1*(n-j)-tj*(n-j-1) = (tj - tj+1)>0,时间减少,这与当前解已是最优解矛盾!
假设第i个打水的人用时为ti,那么总的等待时间就应该是t1*(n-1)+t2*(n-2)+……+tn-1这里我们直接给出一种贪心的策略:按照用时的多少从小到大排队。下面我们证明这种方法的等待时间是最少的。下面假设t1<t2<……tn。假若最优解不是按照时间长短来依次打水,那么一定存在相邻的两个人(记为j和tj+1)满足tj>tj+1。现在我们将这两个人打水的顺序调换,不影响其他人的等待时间,但是我们减少了tj*(n-j)+tj+1*(n-j-1)-tj+1*(n-j)-tj*(n-j-1) = (tj - tj+1)>0,时间减少,这与当前解已是最优解矛盾!
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
//结果可能很大
long long res;
int t[N];int main()
{int n;cin>>n;//因为排序从t这个指针开始,所以我们读入时要从下标0开始读入for(int i = 0;i<n;i++) cin>>t[i];sort(t,t+n);//因为下标从0开始了,所以乘的数要相应地变成(n-i-1)for(int i = 0;i<n;i++) res+=(n-i-1)*t[i];cout<<res;return 0;
}
六.货仓选址

我们首先将坐标按照从小到大的顺序排好。假设选址的位置为x,商店的位置分别为x1,x2,x3,……,xn。那么距离之和f(x)= |x-x1|+|x-x2|+……+|x-xn|。我们将它们两两合成一组,那么就是f(x) = |x-x1|+|x-xn|+|x-x2|+|x-xn-1|+……。根据绝对值不等式,f(x)>=|xn-x1|+|xn-1 - x2|+……而等号恰好可以同时取得(即x在中位数的地方)。如图——

#include <algorithm>
#include<iostream>
using namespace std;const int N = 100005;int n, res;
int a[N];int main()
{cin>>n;for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);sort(a, a + n);for (int i = 0; i < n; i ++ ) res += abs(a[i] - a[n >> 1]);printf("%d\n", res);return 0;
}
七.耍杂技的牛

下面风格给出一种贪心策略:
#include<iostream>
#include<limits.h>
#include<algorithm>
using namespace std;
const int K = 50010;
int sum;
int res = INT_MIN;
typedef pair<int,int> PII;
PII cows[K];
int main()
{int N;cin>>N;for(int i = 0;i<N;i++){int w,s;cin>>w>>s;cows[i] = {w+s,w};}sort(cows,cows+N);for(int i = 0;i<N;i++){int w = cows[i].second,s = cows[i].first - w;res = max(res,sum - s);sum+=w;}cout<<res;return 0;
}
相关文章:

XCPC第十三站,贪心问题
一.区间选点 我们采取这样的策略来选点:step(1)将区间按照右端点的大小从小到大排序;step(2)从前往后依次枚举每个区间,如果当前区间中已经包含点,直接pass,否则选当前区…...
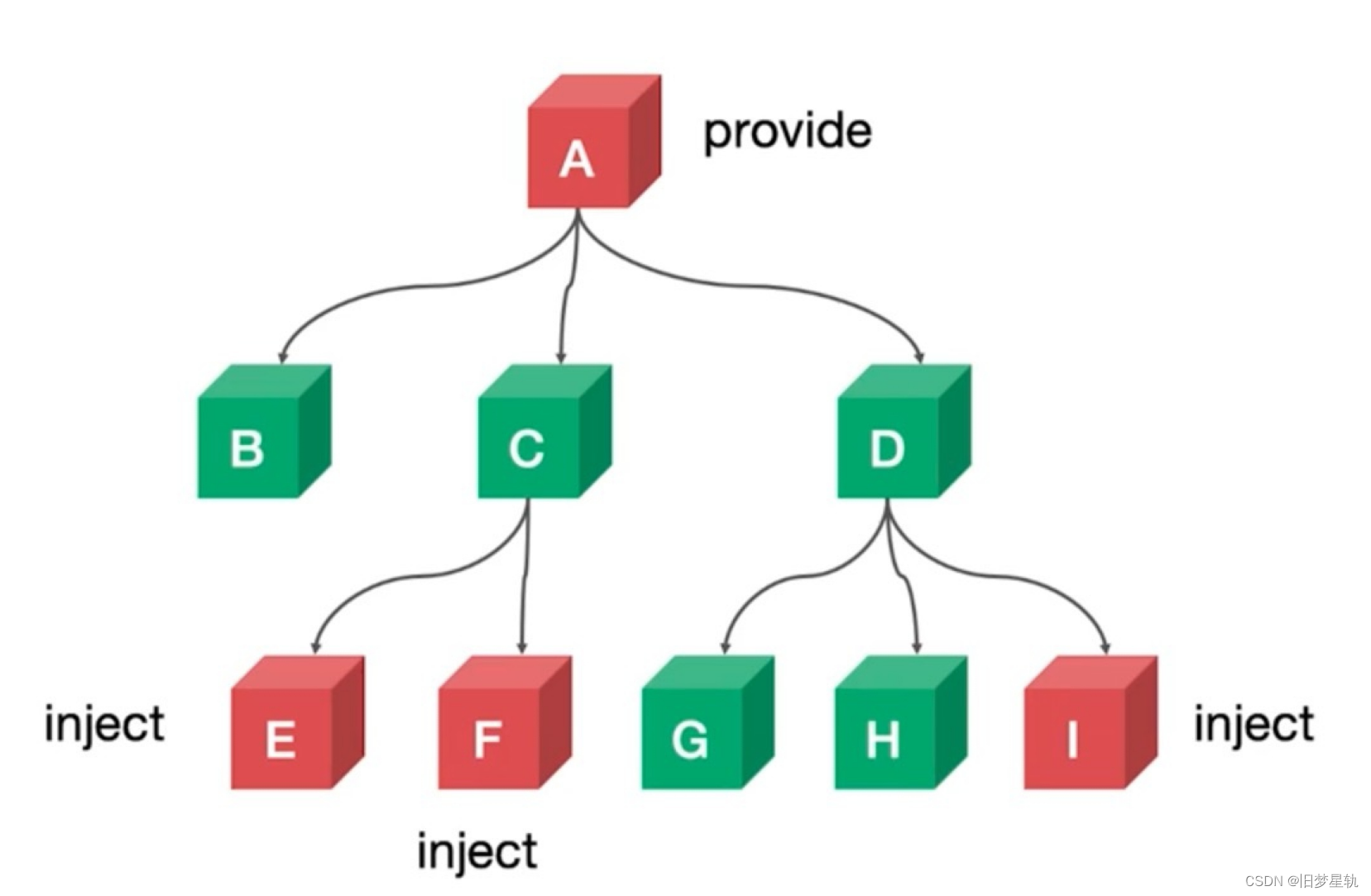
一文让你吃透 Vue3中的组件间通讯 【一篇通】
文章目录前情回顾前言1. 父组件 > 子组件通讯传递2. 子组件 > 父组件通讯传递3. 爷孙组件,后代组件通讯数据总结前情回顾 在本专栏前一章节中,我为大家带来了 Vue3 新特性变化上手指南 的归纳梳理,主要介绍了 Vue3 的 Proxy 响应式原理…...

EVE遭遇大规模DDOS攻击,玩家和官方都傻眼了
如果你恰好是一名《星战前夜》(EVE)的国际服玩家(虽然这个几率很小),又恰好因为疫情一直待在家里,那你就真是倒霉透顶了。因为从1月底开始,EVE的服务器就一直受到大规模的DDOS攻击,而…...
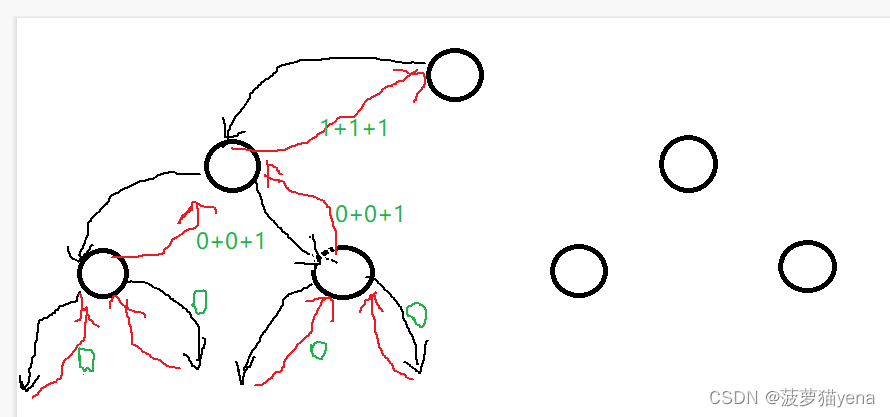
【数据结构】二叉树及相关习题详解
新年新气象! 祝大家兔年 财源滚滚! 万事胜意! 文章目录前言1. 树的一些基础概念1.1 树的一些基本概念1.2 树的一些重要概念2. 二叉树的一些基本概念2.1 二叉树的结构2.2 两种特殊的二叉树3. 二叉树的性质4. 二叉树的存储5. 二叉树的基本操作5.1 构造一棵二叉树5.2 二叉树的遍历…...
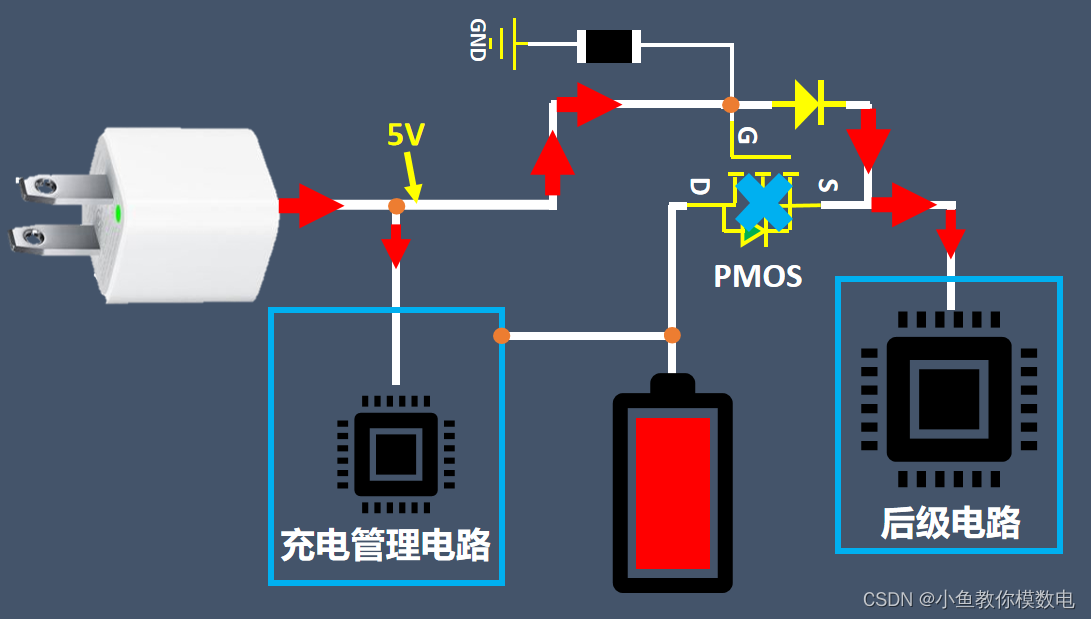
锂电池充电的同时也能放电吗?
大家应该都有这样经历,我们的手机在充电的同时也能边使用,有的同学就会说了,这是因为手机电池在充电的同时也在放电。如果这样想我们可能就把锂电池类比了一个蓄水池,以为它在进水的同时也能出水,其实这个比喻是错误的…...

通信工程考研英语复试专有名词翻译
中文英文频分多址Frequency Division Multiple Access码分多址Code Division Multiple Access时分多址Time Division Multiple Access移动通信mobile communication人工智能artificial intelligence水声通信Middle-Range Uwa Communication正交频分复用Orthogonal frequency di…...

注意力机制(四):多头注意力
专栏:神经网络复现目录 注意力机制 注意力机制(Attention Mechanism)是一种人工智能技术,它可以让神经网络在处理序列数据时,专注于关键信息的部分,同时忽略不重要的部分。在自然语言处理、计算机视觉、语…...

【2023Unity游戏开发教程】零基础带你从小白到超神19——射线检测
文章目录 射线检测从某点发射一条射线从摄像机发射一条射线射线检测 游戏中的红外线,默认肉眼是看不到的,从某个初始点开始,沿着特定的方向发射一条不可见且无限长的射线,通过此射线检测是否有任何模型添加了Collider碰撞器组件。一旦检测到碰撞,停止射线继续发射。 碰撞检…...
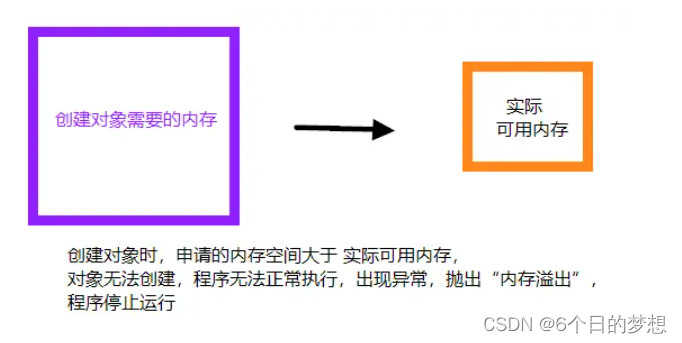
内存泄漏和内存溢出的区别
参考答案 内存溢出(out of memory):指程序在申请内存时,没有足够的内存空间供其使用,出现 out of memory。内存泄露(memory leak):指程序在申请内存后,无法释放已申请的内存空间,内存泄露堆积会导致内存被…...

文本三剑客之sed编辑器
文本三剑客:都是按行读取后处理。 grep 过滤行内容。awk 过滤字段。sed 过滤行内容;修改行内容。sed编辑器 sed是一种流编辑器,流编辑器会在编辑器处理数据之前基于预先提供的一组规则来编辑数据流。 sed编辑器可以根据命令来处理数据流中…...
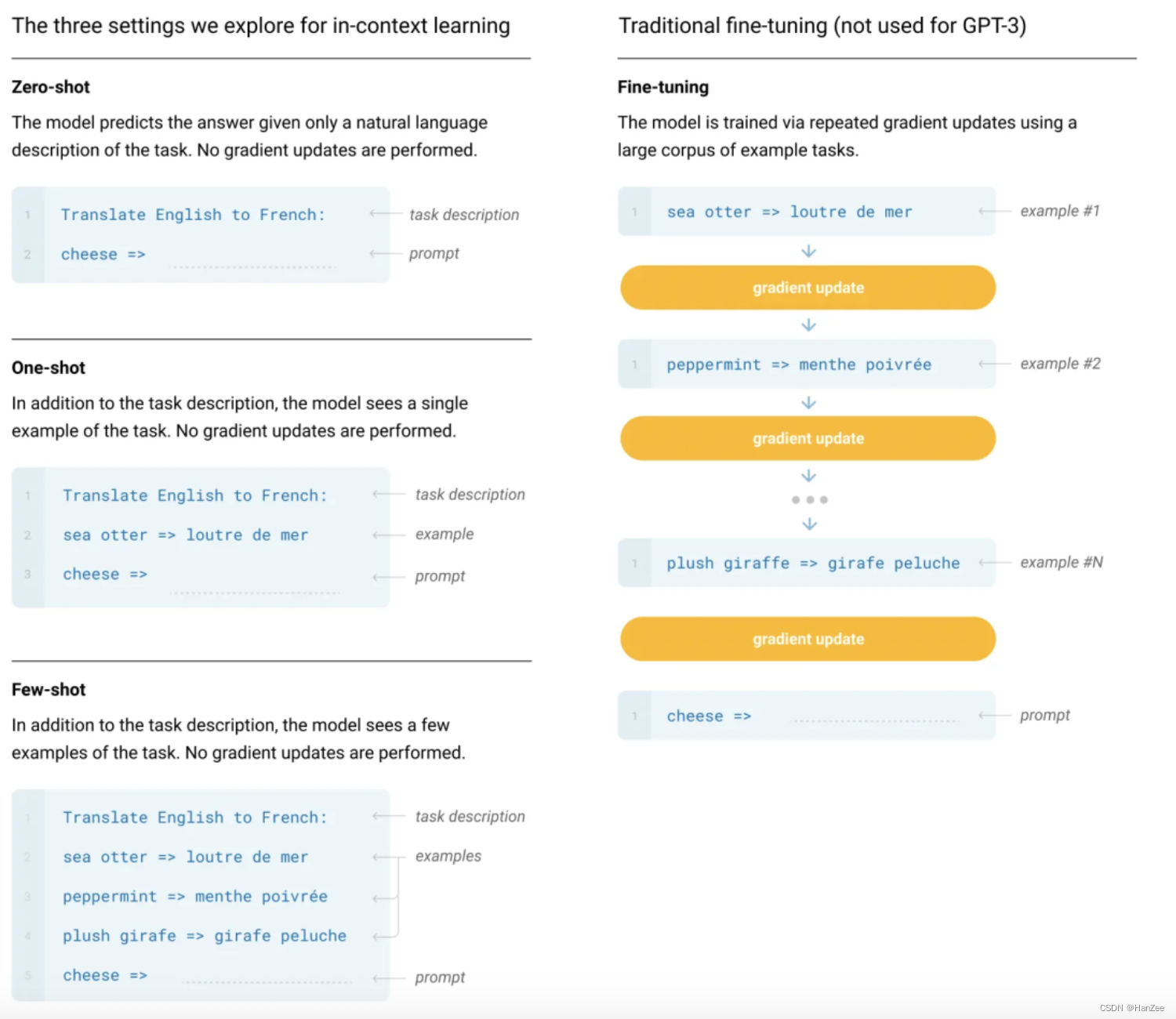
深度学习:GPT1、GPT2、GPT-3
深度学习:GPT1、GPT2、GPT3的原理与模型代码解读GPT-1IntroductionFramework自监督学习微调ExperimentGPT-2IntroductionApproachConclusionGPT-3GPT-1 Introduction GPT-1(Generative Pre-training Transformer-1)是由OpenAI于2018年发布的…...

使用Docker 一键部署SpringBoot和SpringCloud项目
使用Docker 一键部署SpringBoot和SpringCloud项目 1. 准备工作2. 创建Dockerfile3. 创建Docker Compose文件4. 构建和运行Docker镜像5. 验证部署6. 总结Docker是一个非常流行的容器化技术,可以方便地将应用程序和服务打包成容器并运行在不同的环境中。在本篇博客中,我将向您展…...

【数据结构】用栈实现队列
💯💯💯 本篇总结利用栈如何实现队列的相关操作,不难观察,栈和队列是可以相互转化的,需要好好总结它们的特性,构造出一个恰当的结构来实现即可,所以本篇难点不在代码思维,…...
[Netty源码] 服务端启动过程 (二)
文章目录1.ServerBootstrap2.服务端启动过程3.具体步骤分析3.1 创建服务端Channel3.2 初始化服务端Channel3.3 注册selector3.4 端口绑定1.ServerBootstrap ServerBootstrap引导服务端启动流程: //主EventLoopGroup NioEventLoopGroup master new NioEventLoopGroup(); //从E…...

Week 14
代码源每日一题Div2 106. 订单编号 原题链接:订单编号 思路:这题本来没啥思路,直到获得了某位佬的提示才会做( 我们可以用set来维护一些区间,这些区间为 pair 类型,表示没有使用过的编号,每次…...

【微信小程序】-- 使用 Git 管理项目(五十)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

leetcode每日一题:134. 加油站
系列:贪心算法 语言:java 题目来源:Leetcode134. 加油站 题目 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[…...

开放式基金实时排行 API 数据接口
开放式基金实时排行 API 数据接口 多维度参数返回,实时数据,类型参数筛选。 1. 产品功能 返回实时开放式基金排行数据可定义查询基金类型参数;多个基金属性值返回多维指标,一次查询毫秒级返回;数据持续更新与维护&am…...

Android开发中synchronized的实现原理
synchronized的三种使用方式 **1.修饰实例方法,**作用于当前实例加锁,进入同步代码前要获得当前实例的锁。 没有问题的写法: public class AccountingSync implements Runnable{//共享资源(临界资源)static int i0;/*** synchronized 修饰实例方法*/p…...
)
【华为OD机试 2023最新 】 统一限载货物数最小值(C++)
题目描述 火车站附近的货物中转站负责将到站货物运往仓库,小明在中转站负责调度2K辆中转车(K辆干货中转车,K辆湿货中转车)。 货物由不同供货商从各地发来,各地的货物是依次进站,然后小明按照卸货顺序依次装货到中转车,一个供货商的货只能装到一辆车上,不能拆装,但是…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
