第十四届蓝桥杯三月真题刷题训练——第 22 天
目录
第 1 题:受伤的皇后_dfs
题目描述
输入描述
输出描述
输入输出样例
运行限制
代码:
思路:
第 2 题:完全平方数
问题描述
输入格式
输出格式
样例输入 1
样例输出 1
样例输入 2
样例输出 2
评测用例规模与约定
运行限制
代码:
思路:
第 3 题:123_前缀和_二分_long
题目描述
输入描述
输出描述
输入输出样例
评测用例规模与约定
运行限制
代码:
思路:
第 4 题:求阶乘_二分_long
问题描述
输入格式
输出格式
样例输入
样例输出
评测用例规模与约定
运行限制
代码:
思路:
第 1 题:受伤的皇后_dfs
题目描述
有一个 n×n 的国际象棋棋盘(n 行 n 列的方格图),请在棋盘中摆放 n 个受伤的国际象棋皇后,要求:
- 任何两个皇后不在同一行。
- 任何两个皇后不在同一列。
- 如果两个皇后在同一条 45 度角的斜线上,这两个皇后之间行号的差值至少为 3 。
请问一共有多少种摆放方案。
输入描述
输入的第一行包含一个整数 n。
其中,1≤n≤10。
输出描述
输出一个整数,表示答案。
输入输出样例
示例 1
输入
4输出
2运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
代码:
package 第十四届蓝桥杯三月真题刷题训练.day22;import java.util.Scanner;/*** @author yx* @date 2023-03-25 14:52*/
public class 受伤的皇后_dfs {static int[][]map;static int ans=0;static int n;static int[] column;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n=scanner.nextInt();map=new int[n][n];column=new int[n];dfs(0);System.out.println(ans);}static void dfs(int i){if(i==n){//出口ans++;}//编列第i行的每一列for (int j = 0; j < n; j++) {if(check(i,j)){//第i行的皇后在第j列column[i]=j;//继续下一行遍历dfs(i+1);}}}//检查r行,l列是否可以放皇后static boolean check(int r,int l){for (int i = 0; i < r ; i++) {//在同一列,在斜对角(注意:因为i!=r所以不用判断在同一行)if(l==column[i]||(Math.abs(r-i)==Math.abs(l-column[i])&&(r-i)<3)){return false;}}return true;}
}
思路:
(1)核心思想是dfs深度搜索
(2)注意dfs必须要有一个出口
if(i==n){//出口ans++;}(3)检查r行l列是否可以放
//检查r行,l列是否可以放皇后static boolean check(int r,int l){for (int i = 0; i < r ; i++) {//在同一列,在斜对角(注意:因为i!=r所以不用判断在同一行)if(l==column[i]||(Math.abs(r-i)==Math.abs(l-column[i])&&(r-i)<3)){return false;}}return true;}(4)因为我们是遍历每一行,所以行是已知的,定义一个数组存储每一行的列值
column=new int[n];
第 2 题:完全平方数
问题描述
一个整数 a 是一个完全平方数, 是指它是某一个整数的平方, 即存在一个 整数 b, 使得 a=b2。
给定一个正整数 n, 请找到最小的正整数 x, 使得它们的乘积是一个完全平 方数。
输入格式
输入一行包含一个正整数 n 。
输出格式
输出找到的最小的正整数 x 。
样例输入 1
12
样例输出 1
3
样例输入 2
15
样例输出 2
15
评测用例规模与约定
对于 30 的评测用例, 1≤n≤1000, 答案不超过 1000 。
对于 60 的评测用例, 1≤n≤10^8, 答案不超过 10^8 。
对于所有评测用例, 1≤n≤10^12, 答案不超过 10^12 。
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
代码:
package 第十四届蓝桥杯三月真题刷题训练.day22;import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Scanner;/*** @author yx* @date 2023-03-25 12:35*/
public class 完全平方数 {static PrintWriter out =new PrintWriter(System.out);static BufferedReader ins=new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer in=new StreamTokenizer(ins);/*** 输入* in.nextToken()* int a= (int)in.nval;** 输出* out.print();* out.flush();** 读文件:* BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream("C:\\Users\\yx\\Desktop\\primes.txt")));* String s = br.readLine();s读取每一行数据* if (s == null)break;读取文件终止的语句**/public static void main(String[] args) {Scanner scanner = new Scanner(System.in);long n=scanner.nextLong();/*1、找一个x使得x*n为一个平方数2、注意数据类型要用long3、如何找出这个最小数x呢,如果n是由a*a*b*b.....*y(y为不能开方的数)组成的话4、那我们是不是把x赋值为y,就可以保证n是完全平方数了,其中a、b都是小于等于sqrt(n)的*/for (long i = 2; i*i <= n ; i++) {//如果这个n由(i*i)^k组成,就一直除到它没有i的平方为止while (n%(i*i)==0)n/=(i*i);}System.out.println(n);}
}
思路:
(1)找一个x使得x*n为一个平方数
(2)注意数据范围要用long
(3)如何找出这个最小数x呢,如果n是由a*a*b*b.....*y(y为不能开方的数)组成的话
(4)那我们是不是最后只需要把y赋值给x,就可以保证x*n是完全平方数了
注意:
while (n%(i*i)==0)n/=(i*i);
第 3 题:123_前缀和_二分_long
题目描述
小蓝发现了一个有趣的数列,这个数列的前几项如下:
1,1,2,1,2,3,1,2,3,4,⋯
小蓝发现,这个数列前 1 项是整数 1,接下来 2 项是整数 1 至 2,接下来 3 项是整数 1 至 3,接下来 4 项是整数 1 至 4,依次类推。
小蓝想知道,这个数列中,连续一段的和是多少。
输入描述
输入的第一行包含一个整数 T,表示询问的个数。
接下来 T 行,每行包含一组询问,其中第 i 行包含两个整数 li 和 ri ,表示询问数列中第 li 个数到第 ri 个数的和。
输出描述
输出 T 行,每行包含一个整数表示对应询问的答案。
输入输出样例
示例
输入
3 1 1 1 3 5 8输出
1 4 8评测用例规模与约定
对于 10% 的评测用例,1≤T≤30,1≤li≤ri≤100。
对于 20% 的评测用例,1≤T≤100,1≤li≤ri≤1000。
对于 40% 的评测用例,1≤T≤1000,1≤li≤ri≤10^6。
对于 70% 的评测用例,1≤T≤10000,1≤li≤ri≤10^9。
对于 80% 的评测用例,1≤T≤1000,1≤li≤ri≤10^12。
对于 90% 的评测用例,1≤T≤10000,1≤li≤ri≤10^12。
对于所有评测用例,1≤T≤100000,1≤li≤ri≤10^12。
运行限制
- 最大运行时间:5s
- 最大运行内存: 256M
代码:
package 第十四届蓝桥杯三月真题刷题训练.day22;import java.io.*;/*** @author yx* @date 2023-03-25 13:56*/
public class 一23_二分 {static PrintWriter out = new PrintWriter(System.out);static BufferedReader ins = new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer in = new StreamTokenizer(ins);static long[] S = new long[1500000];//大区间static long[] a = new long[1500000];//小区间/*** 输入* in.nextToken()* int a= (int)in.nval;* <p>* 输出* out.print();* out.flush();* <p>* 读文件:* BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream("C:\\Users\\yx\\Desktop\\primes.txt")));* String s = br.readLine();s读取每一行数据* if (s == null)break;读取文件终止的语句**/public static void main(String[] args) throws IOException {for (int i = 1; i < 1500000; i++) {a[i] = a[i - 1] + i;//对小区间前缀和S[i] = S[i - 1] + a[i];//对大区间前缀和}//注意数据类型longin.nextToken();int n = (int) in.nval;while (n != 0) {n--;String[] sp = ins.readLine().split(" ");long l = Long.parseLong(sp[0]);long r = Long.parseLong(sp[1]);String ans = (Sum(r) - Sum(l - 1)) + "";System.out.println(ans);}}//求整体前缀和static long Sum(long m) {if (m == 0) return 0;//1、用等差数列求和公式是O(n^1/2)的复杂度
// int i = 1;
// //找i的区间位置
// while (true){
// if(((long)i*(long)(i+1)/2)>=m){
// break;
// }
// i++;
// }//2、二分优化long l=1;long r=1500000;long ans=1;while (l <= r) {//二分long mid = (l + r) / 2;if (a[(int) mid]<m) {ans = mid;l = mid + 1;} else {r = mid - 1;}}
// System.out.print(ans);
// ans--;return S[(int) ans ] + a[(int) (m - a[(int) ans ])];}
}
思路:
(1)这道题目和核心思想是前缀和
(2)直接求所有数据的前缀和的话我们不好求,一个是数据下标会爆炸(下标不可能是10^12)
(3)我用把它进行划分多个大区间:1为第一个大区间;1 2为第二个大区间;1 2 3为第三个大区间;1 2 3 4为第四个大区间......
(4)我们用S把每一个大区间的和进行存储
(5)再定义一个小区间a,a可以用来定位也可以用来迭代数据
- 定位:输入一个m,我们通过与a[i]的比较能快速找到第m个数位于第i个大区间
- 迭代数据:用于S数组初始化迭代数据;用于输出第i个大区间的第j位(j=m-a[i])前缀和
(6)因为每个大区间个数呈等差数列增长,我们通过(n)*(n+1)/2这个公式来定位m的位置,复杂度为O(
),最后能通过8个点,超时2个点
//1、用等差数列求和公式是O(n^1/2)的复杂度 // int i = 1; // //找i的区间位置 // while (true){ // if(((long)i*(long)(i+1)/2)>=m){ // break; // } // i++; // }(7)用二分进行优化复杂度O(logN)
//2、二分优化long l=1;long r=1500000;long ans=1;while (l <= r) {//二分long mid = (l + r) / 2;if (a[(int) mid]<m) {ans = mid;l = mid + 1;} else {r = mid - 1;}} // System.out.print(ans); // ans--;return S[(int) ans ] + a[(int) (m - a[(int) ans ])];
第 4 题:求阶乘_二分_long
问题描述
满足 N ! 的末尾恰好有 K 个 0 的最小的 N 是多少?
如果这样的 N 不存在输出 −1 。
输入格式
一个整数 K 。
输出格式
一个整数代表答案。
样例输入
2样例输出
10评测用例规模与约定
对于 30% 的数据, 1≤K≤10^6
对于 100% 的数据, 1≤K≤10^18
运行限制
- 最大运行时间:3s
- 最大运行内存: 512M
代码:
package 第十四届蓝桥杯三月真题刷题训练.day22;import java.util.Scanner;/*** @author yx* @date 2023-03-25 13:02*/
public class 求阶乘_二分 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);//注意数据范围用longlong K = scanner.nextLong();
// long r = 1000000000000000000L;long r = 9000000000000000000L;long l = 1;long ans=0;while (l <= r) {long mid = (l + r) / 2;if (Find_5(mid)<K) {
// System.out.println(Find_5(mid));ans = mid;l = mid + 1;} else {r = mid - 1;}}if(Find_5(ans+1)==K) {System.out.print(ans + 1);}else {System.out.println(-1);}}//末尾1个0对应一个因子5和一个因子2.因为2的个数是远远大于5的个数的所以只需要找5有多少即可static long Find_5(long n) {long ans = 0;//为什么要循环除5呢?/*我们举一个例子: n=100时(1) n/5=20;表示在1~n有20个区间大小为5的区间(5只能分解一个5)(2) (n/5)/5=4;表示在1~n有4个区间大小为25的区间(25可以分解两个5)(3)((n/5)/5)/5=0;表示1~n有0个区间大小为125的区间(125可以分解3个5)*/while (n / 5 != 0) {n /= 5;ans += n;}return ans;}
}

思路:
(1)数据范围long
(2)末尾1个0对应一个因子5和一个因子2,又由于2的个数是远远大于5的个数的所以只需要找5有多少即可
static long Find_5(long n)(3)在Find_5这个函数里为什么要循环除5呢?
我们举一个例子: n=100时 (1) n/5=20;表示在1~n有20个区间大小为5的区间(5只能分解一个5) (2) (n/5)/5=4;表示在1~n有4个区间大小为25的区间(25可以分解两个5) (3)((n/5)/5)/5=0;表示1~n有0个区间大小为125的区间(125可以分解3个5)(4)最后用二分来找n(二分模板)
while (l <= r) {long mid = (l + r) / 2;if (Find_5(mid)<K) { // System.out.println(Find_5(mid));ans = mid;l = mid + 1;} else {r = mid - 1;}}(5)注意这道题目中二分的r的初始值,如果用Long.MaxValue是只能过9个点的,因为Long.MaxValue的取值是2^63-1,而long的范围2^64-1,所以初始值r应该是2^64-1才可以
// long r = 1000000000000000000L; // long r=Long.MAX_VALUE;long r = 9000000000000000000L;
相关文章:

第十四届蓝桥杯三月真题刷题训练——第 22 天
目录 第 1 题:受伤的皇后_dfs 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思路: 第 2 题:完全平方数 问题描述 输入格式 输出格式 样例输入 1 样例输出 1 样例输入 2 样例输出 2 评测用例规模与约…...
机器学习:朴素贝叶斯模型算法原理(含实战案例)
机器学习:朴素贝叶斯模型算法原理 作者:i阿极 作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏&…...

Linux 多线程:理解线程
目录一、理解线程的思想二、Linux中的线程与进程1.Linux中的进程2.Linux中的线程三、线程的工作方式四、线程的独有数据与共享数据1.独有数据2.共享数据一、理解线程的思想 线程就是把一个进程分成多个执行部分,一个部分就是一个线程,比如可以让一个线程…...
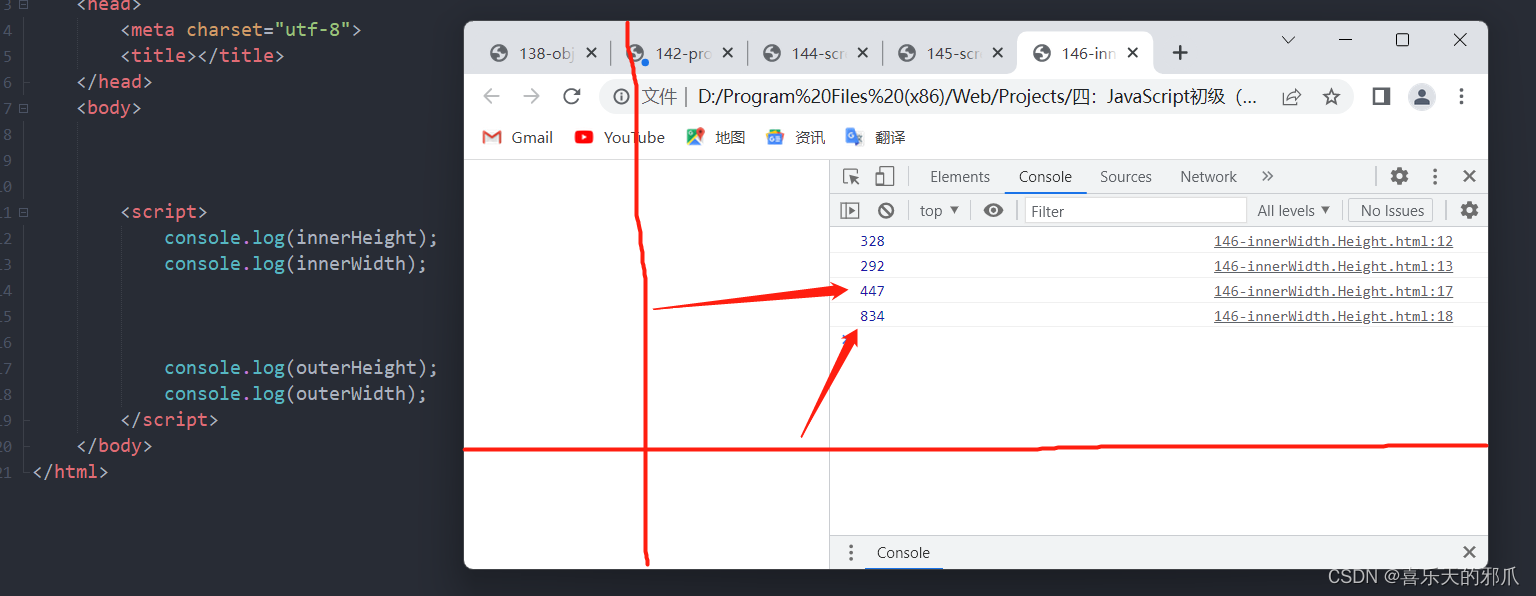
Web前端学习:章四 -- JavaScript初级(四)-- BOM
138:Object数据格式简介 1、object对象 JS中独有 的一种数据格式 名字可以随便取,值一般就那几种数据格式 139:BOM - JS跳转页面 BOM Browser Object Model:浏览器对象模型 使用JavaScript控制浏览器交互 控制浏览器里面的内…...

Lesson9.网络基础1
网络协议初识 所谓的协议就是人们为了通信的一种约定 操作系统要进行协议管理,必然会先描述,再组织协议本质就是软件,软件是可以"分层"协议在设计的时候,就是被层状的划分的, 为什么要划分成为层状结构 场景复杂功能解耦(便于人们进行各种维护)OSI七层模型 局域网中…...
这几个SQL语法的坑,你踩过吗
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...

算法基础——复杂度
前言 算法是解决问题的一系列操作的集合。著名的计算机科学家Niklaus Wirth曾提出:算法数据结构程序,由此可见算法在编程中的重要地位。本篇主要讨论算法性能好坏的标准之一——复杂度。 1 复杂度概述 1.1 什么是复杂度 本文所讨论的复杂度是指通过事先…...

基类与派生类对象的关系 派生类的构造函数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
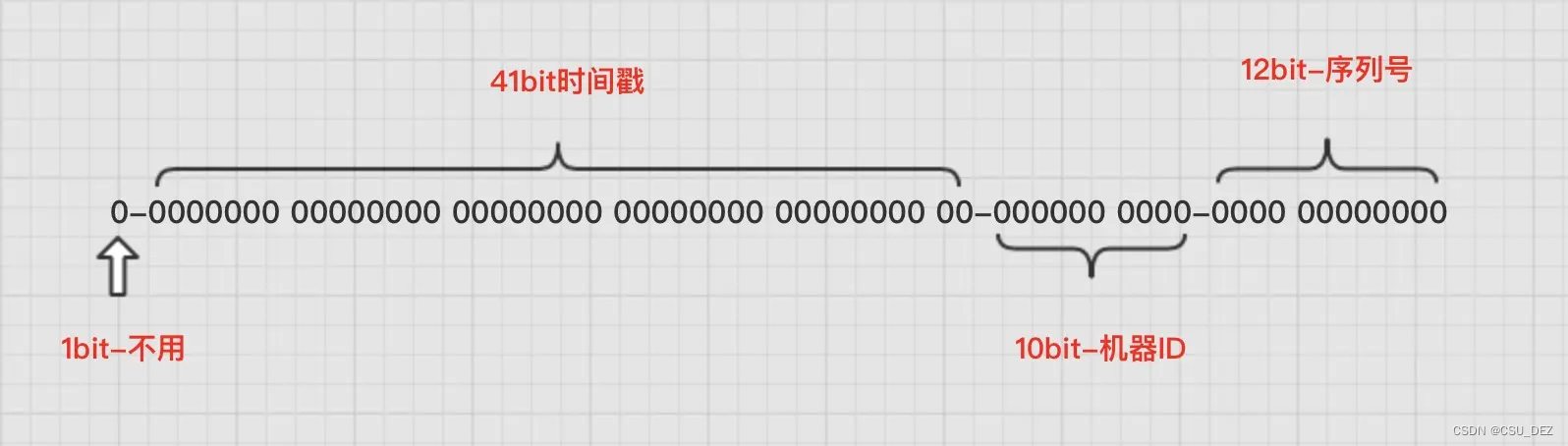
【算法】生成分布式 ID 的雪花算法
ID 是数据的唯一、不变且不重复的标识,在查询数据库的数据时必须通过 ID 查询,在分布式环境下生成全局唯一的 ID 是一个重要问题。 雪花算法(snowflake)是一种生成分布式环境下全局唯一 ID 的算法,该算法由 Twitter 发…...
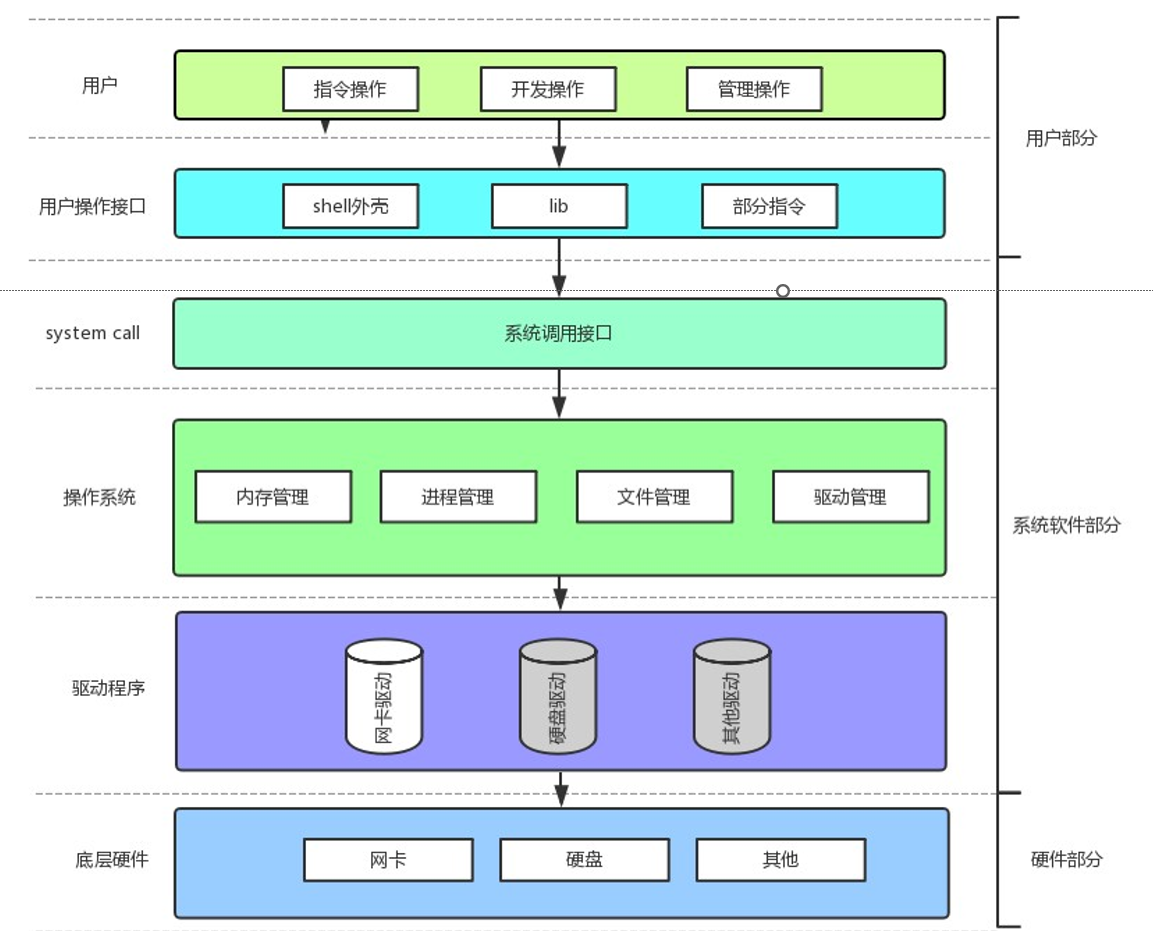
Linux系统编程 - 基础IO(IO操作)
目录 预备知识 复习C文件IO相关操作 printf相关函数 fprintf snprintf 读取文件 系统文件IO操作 open函数 umask()函数 open函数返回值 预备知识 1.你真的理解文件原理和操作了吗?不是语言问题,是系统问题2.是不是只有C/C有文件操作呢&#x…...

基于 Avue 的 CRUD 表格组件封装
在 components 文件夹中,创建一个新的 .vue 文件,例如:AvueCrudTable.vue。 透传父组件传递的属性和事件 : 1、利用v-bind=“ a t t r s " 支持所有 a v u e 的使用方法并在其基础上进行封装 2 、使用 v − o n = " attrs"支持所有 avue 的使用方法并在其基…...
基于框架编写驱动代码)
树莓派学习笔记(十三)基于框架编写驱动代码
文章目录一、代码分析:二、源码一、代码分析: 在内核中由于代码文件多,避免函数名重复,使用static将函数的作用域限制在该文件内 内核的打印函数printk和printf类似 file_operations结构体使用符号“ . ”指定参数,省…...
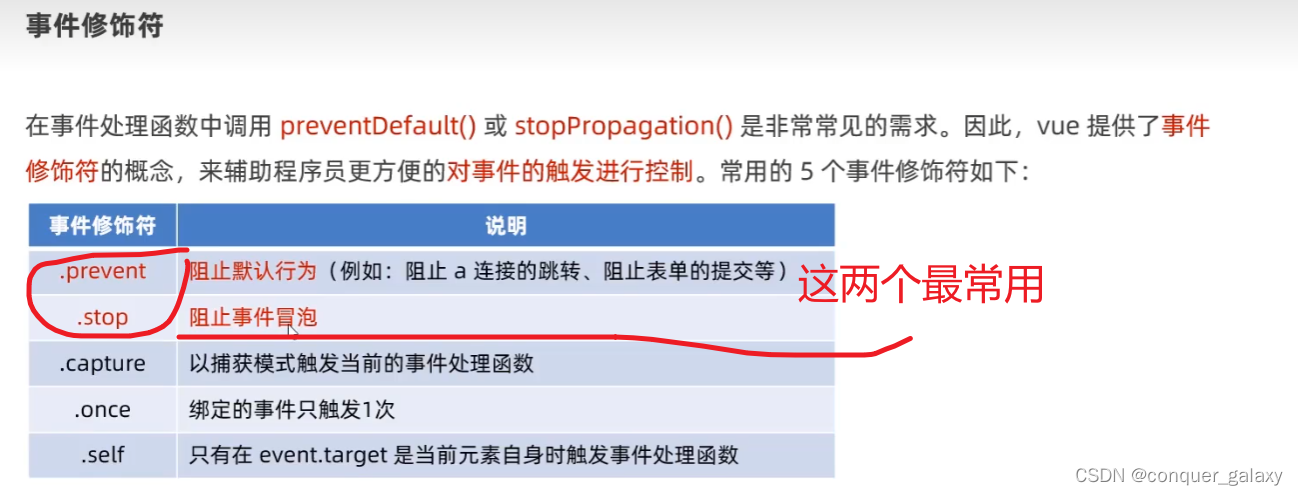
vue事件修饰符之.prevent
.prevent 事件修饰符只是阻止默认事件,不会自动触发任何事件处理函数。因此,在使用 .prevent 事件修饰符时,需要自己编写相应的事件处理函数来处理事件。 例如,在上面的例子中,我们通过在表单上绑定 submit.prevent&q…...

【SpringCloud AlibabaSentinel实现熔断与限流】
本笔记内容为尚硅谷SpringCloud AlibabaSentinel部分 目录 一、Sentinel 1、官网 2、Sentinel是什么 3、下载 4、特性 5、使用 二、安装Sentinel控制台 1、sentinel组件由2部分构成 2、安装步骤 1.下载 2.运行命令 3.访问sentinel管理界面 三、初始化演示工程 …...

类与对象-封装
一、封装的意义封装是C面向对象三大特性之一语法: class name { 访问权限:属性行为 };注意:类中的属性和行为 统称为成员属性 又称 成员属性 / 成员变量行为 又称 成员函数 / 成员方法封装将属性和行为作为一个整体,表现生活中的事物例①&…...

【回忆杀】2012年拥有第一台电脑【致逝去的青春】
高中说起 在2012年的时候吧,高考过后,那个时候一门心思的想当一名体育老师【现在居然还有这个想法,哈哈】,最后没有考上自己希望的大学我记得好像是2012年7月的时候就去重庆投靠朋友,他教我做模具,2012年做…...

PointNeXt: Revisiting PointNet++ with Improved Training and Scaling Strategies
Abstract PointNet 是点云理解领域最有影响力的神经网络架构之一。虽然近期出现了 PointMLP 和 Point Transformer 等新型网络,它们的精度已经大大超过了 PointNet,但我们发现大部分性能提升是由于改进的训练策略,例如数据增强和优化技术以及…...
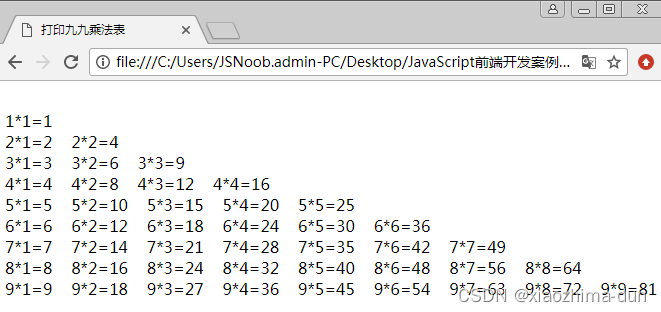
打印九九乘法表-课后程序(JavaScript前端开发案例教程-黑马程序员编著-第2章-课后作业)
【案例2-9】打印九九乘法表 一、案例描述 考核知识点 for双重循环 练习目标 掌握for循环应用。实现九九乘法表。 需求分析 九九乘法表相信大家一点也不陌生,之前见到的乘法表是印刷在课程本之上的。而在本案例中我们将用JavaScript代码来实现九九乘法表。 案例分…...
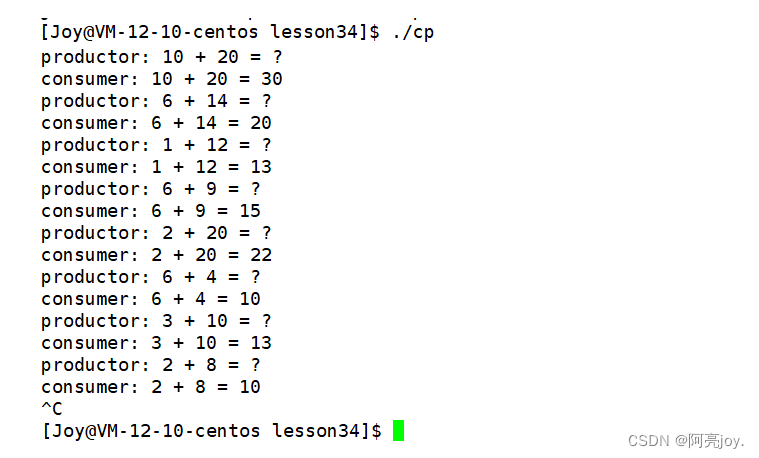
【Linux】基于阻塞队列的生产者消费者模型
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉为何要使用…...
)
【华为OD机试 2023最新 】 真正的密码(C++)
文章目录 题目描述输入描述输出描述用例题目解析C++题目描述 在一行中输入一个字符串数组,如果其中一个字符串的所有以索引0开头的子串在数组中都有,那么这个字符串就是潜在密码, 在所有潜在密码中最长的是真正的密码,如果有多个长度相同的真正的密码,那么取字典序最大的…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...

构建Docker镜像的Dockerfile文件详解
文章目录 前言Dockerfile 案例docker build1. 基本构建2. 指定 Dockerfile 路径3. 设置构建时变量4. 不使用缓存5. 删除中间容器6. 拉取最新基础镜像7. 静默输出完整示例 docker runDockerFile 入门syntax指定构造器FROM基础镜像RUN命令注释COPY复制ENV设置环境变量EXPOSE暴露端…...

