【数据结构】堆
文章目录
- 前言
- 堆的概念及结构
- 堆初始化
- 堆的判空
- 堆的销毁
- 插入数据
- 删除数据
- 堆的数据个数
- 获取堆顶数据
- 用数组创建堆
- 对数组堆排序
- 有关topk问题
- 整体代码展示
- 写在最后
前言
🚩前面了解了树(-> 传送门 <-)的概念后,本章带大家来实现一个跟树有关的数据结构——堆(本章有对堆排序和
topk问题的讲解)。
🚩普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把 堆 (一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
如下图:
🚩所以,我们在实现 堆 的时候可以将它看作为一棵二叉树来思考,这是它的 逻辑结构 。但其 物理结构 是一个实实在在的 顺序数组 (在内存当中存储的形式)。
🚩那么接下来就开始实现一个属于自己的堆吧!
堆的概念及结构
-
本章是以大堆为例,只要会了大堆,小堆也是不在话下。
-
堆是把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且它的任意元素 Ki(i = 0, 1, 2, 3, …, n - 1) 都满足 Ki <= K(i * 2 + 1) 且 Ki <= (i * 2 + 2) ( 或者 Ki >= K(i * 2 + 1) 且 Ki >= K(i * 2 + 2) ),这样的堆我们称之为 小堆( 或者 大堆 )。我们还可以将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
-
有了对堆的概念和性质的理解,相信大家对堆的元素是如何在数组中存储的(物理结构)明白了许多,就是依照上面大堆小堆的概念来维持存储关系的。
图示:
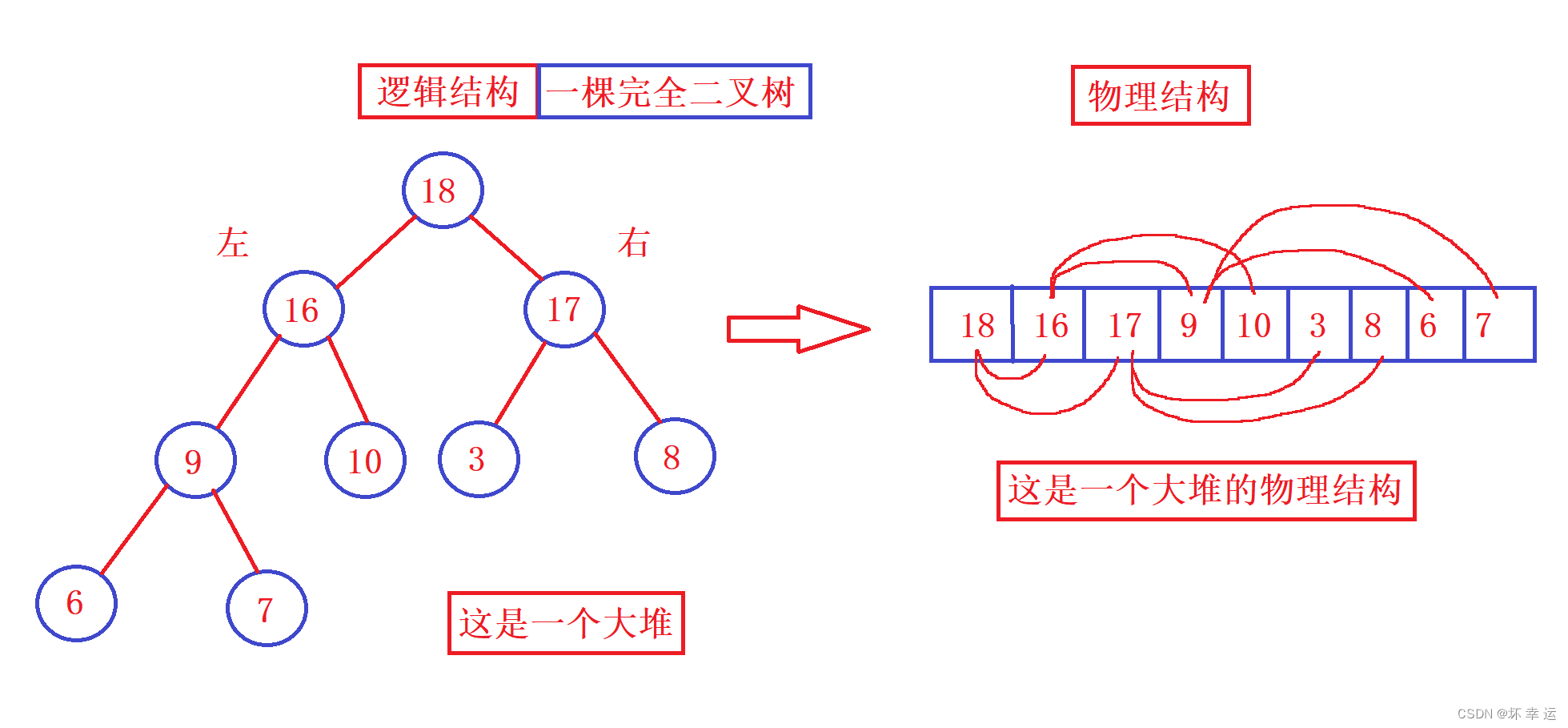
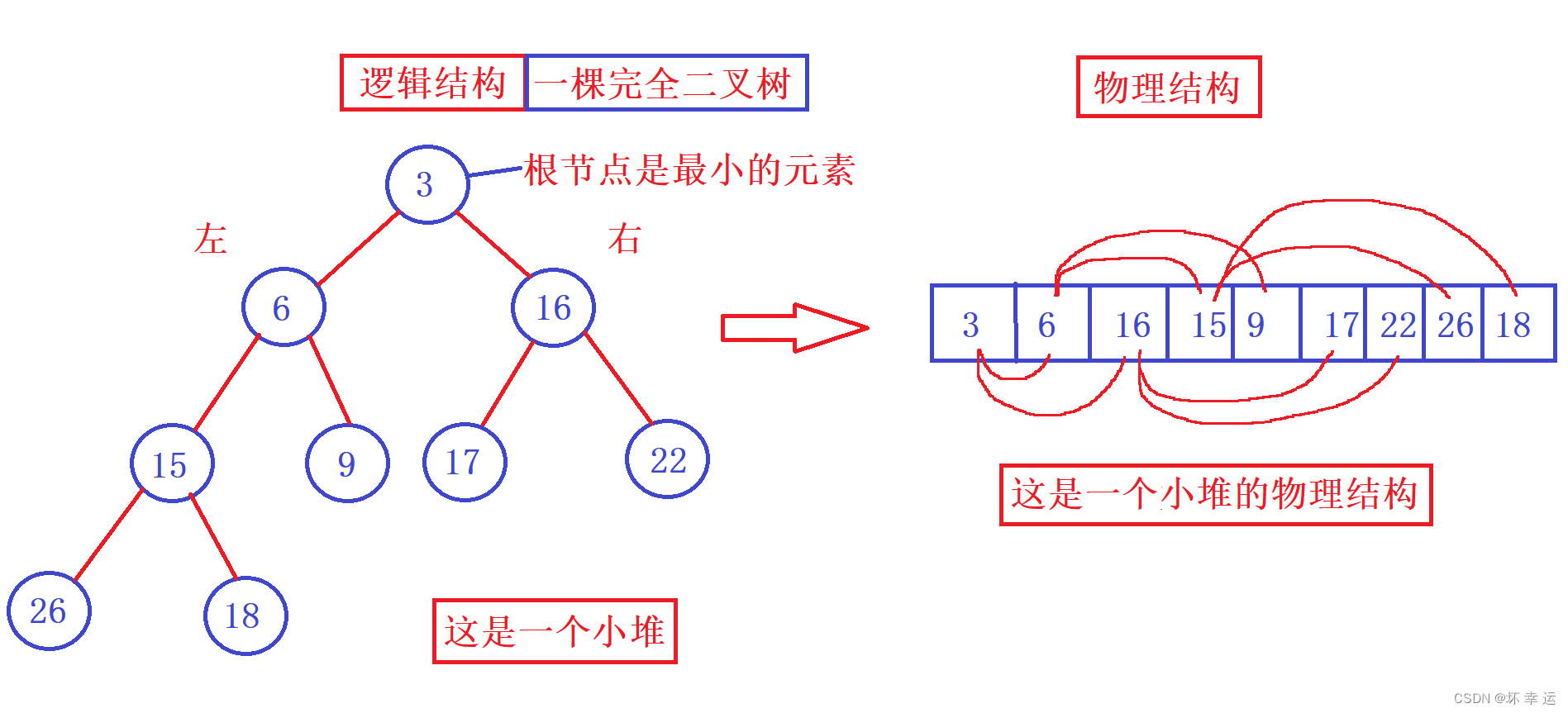
- 观察上图可知,第一张图是一个大堆的逻辑结构和物理结构,其每个结点的左右子结点都比这个结点要小或者等于;第二张图是一个小堆的逻辑结构和物理结构,其每个结点的左右子结点都比这个结点要大或者等于。所以,一个堆,他只能是小堆或者大堆,不具有这两个堆的性质的,都不属于堆,下面我们来判断一下那些是堆那些不是堆:
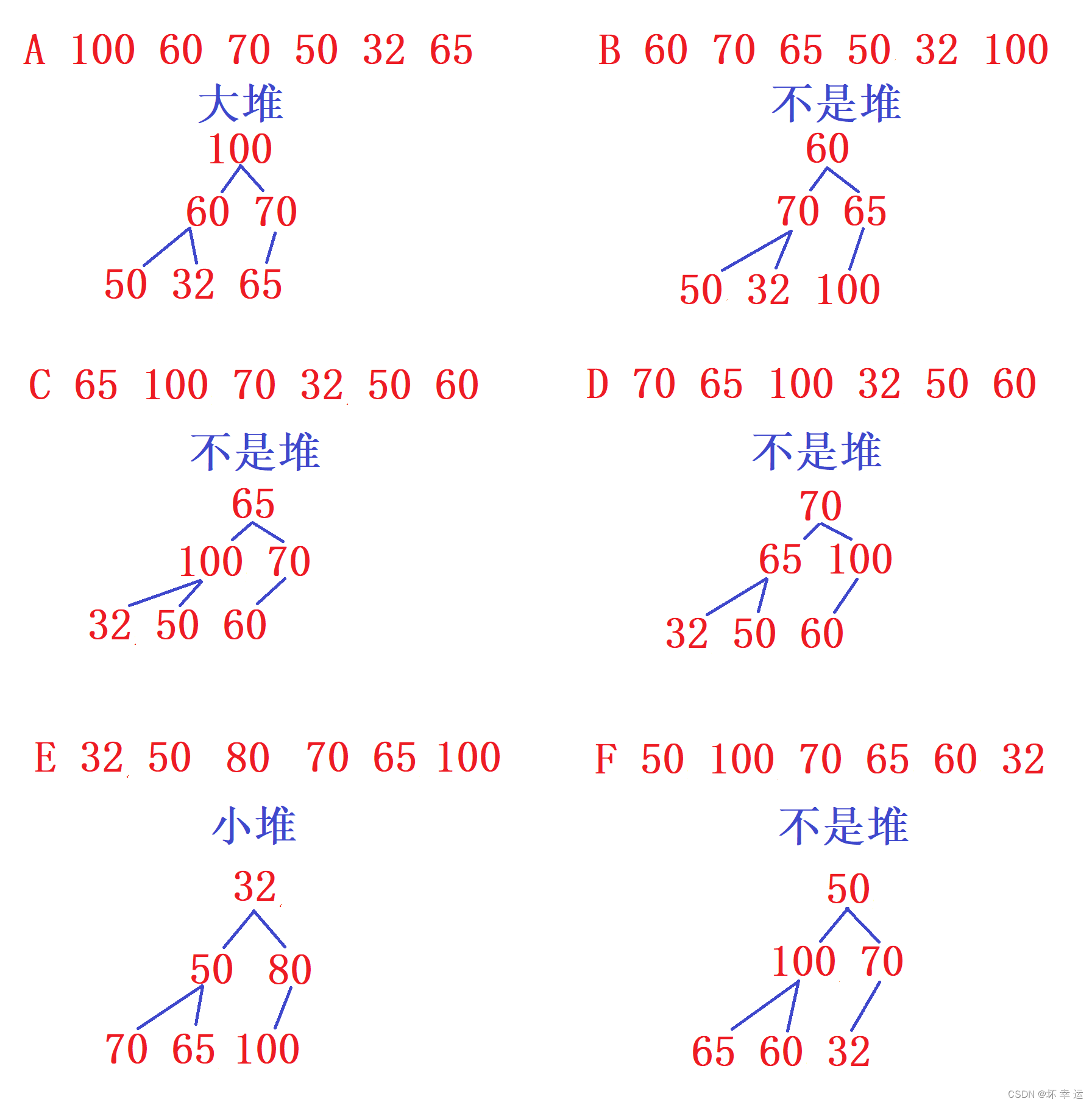
A. 100,60,70,50,32,65 // 这是一个大堆
B. 60,70,65,50,32,100 // 这不是堆
C. 65,100,70,32,50,60 // 这不是堆
D. 70,65,100,32,50,60 // 这不是堆
E. 32,50,80,70,65,100 // 这是一个小堆
F. 50,100,70,65,60,32 // 这不是堆
其实如果想要更好的判断,只需要将其逻辑结构画出来,就一目了然了。

了解了堆的概念和结构后,接下来就是实现啦!!!
堆初始化
- 首先我们需要三个文件:
heap.h,heap.c,test.c。heap.h用来存放所需头文件,堆的结构体和相关函数声明。heap.c用来实现相关函数接口,test.c用来测试。
下面是所需头文件:
#include <stdio.h>
// assert断言所需
#include <assert.h>
// 动态内存开辟函数所需
#include <stdlib.h>
// bool类型所需
#include <stdbool.h>
// 拷贝函数所需
#include <string.h>
- 我们知道,堆的底层存储结构是一个顺序的数组,因此这里需要跟前面我们实现的顺序表一样用动态内存空间。使用动态空间,就需要一个变量来统计容量,当然,为了后面一些函数功能的需求,还需要一个变量来统计堆的数据个数。因此,一个堆的结构定义如下:
// 堆的元素的数据类型
typedef int HPDataType;
typedef struct Heap
{// 指向存储数据的连续的空间(数组)HPDataType* a;// 统计当前堆中数据的个数int size;// 统计当前空间的容量int capacity;
}Heap;
- 一个堆所需的函数接口声明如下:
// 以大堆为例
// 堆初始化
void HeapInit(Heap* php);
// 数组创建堆
void HeapCreateArray(Heap* php, HPDataType* a, int n);// 插入数据
void HeapPush(Heap* php, HPDataType x);
// 删除数据
void HeapPop(Heap* php);// 获取堆顶数据
HPDataType HeapTop(Heap* php);// 获取堆数据个数
int HeapSize(Heap* php);// 堆判空
bool HeapEmpty(Heap* php);// 堆的销毁
void HeapDestroy(Heap* php);// 交换
void swap(HPDataType* a, HPDataType* b);
// 向上调整
void adjustup(HPDataType* a, int child);
// 向下调整
void adjustdown(HPDataType* a, int size, int parent);// 堆排序
void HeapSort(HPDataType* a, int n);
// topk问题
void PrintTopK(HPDataType* a, int n, int k);
- 有了以上的铺垫,堆的初始化就是将堆的结构里的指针置为空,统计数据个数和统计空间容量的变量置为
0即可。(当然也可以初始化的时候就开个初始空间)
相关函数接口功能的实现:
// 堆初始化
void HeapInit(Heap* php)
{// 防止传递一个NULL上来,传NULL的话php就是NULL,后面的操作就不能进行了assert(php);php->a = NULL;php->capacity = php->size = 0;
}
堆的判空
- 有了统计堆的数据个数的变量
size,判空就简单多了。只需要判断一下size是否为0即可,如果size为0,说明为空,返回true,如果size不为0,说明堆中有数据,返回false。
相关函数接口功能的实现:
// 堆判空
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}
堆的销毁
- 堆的销毁也很简单,将堆空间释放即可。当然
size跟统计容量的capacity也置为0。
相关函数接口功能的实现:
// 堆的销毁
void HeapDestroy(Heap* php)
{assert(php);free(php->a);php->capacity = php->size = 0;
}
插入数据
-
首先,插入数据要看看容量够不够,如果不够,就需要扩容。
-
插入数据就是在数组的最后一个位置插入,由于
size是数据的个数也就是数组的长度,所以size就是指向堆的最后一个数据的下一个位置,因此我们只需要在size位置插入即可。当然,插入过后,多了一个数据,因此size要自加1。 -
当我们插入数据之后,现在堆的结构很可能就不是一个堆(以大堆为例)了,因此,这里需要对插入进来的那个数据执行一个向上调整的算法,图示:

- 对于向上调整算法,我们需要找到这个结点(假设下标为
child)的父亲结点(假设下标为parent),具体操作为:parent = (child - 1) / 2 ,找到父结点后,就与他进行比较,由于我们以大堆为例,所以如果child位置上的数据大于parent位置上的数据,就需要将这两个数据交换一下,然后循环往复,继续寻找父结点进行比较,直到到达应该处在的位置为止(直到是个堆为止)。
相关函数接口功能的实现:
// 插入数据
void HeapPush(Heap* php, HPDataType x)
{assert(php);// 如果容量满了就扩容if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}// 在size位置插入数据,然后size自加1php->a[php->size++] = x;// 对插入的那个数据执行向上调整算法,重整堆// php->size - 1是插入的那个数据的下标adjustup(php->a, php->size - 1);
}
向上调整算法:
// 向上调整
void adjustup(HPDataType* a, int child)
{// 找父结点int parent = (child - 1) / 2;while (child > 0){// 如果child位置的数据大小大于parent位置的数据大小就交换if (a[child] > a[parent]){// 交换swap(&a[child], &a[parent]);// 交换过后,child依旧指向开始指向的那个数据child = parent;// 继续找父结点parent = (child - 1) / 2;}else break; // 如果小于等于了,说明此时的堆是个真正的堆了,直接跳出循环}
}
这里有个swap函数,其实现为:
// 交换
// 注意是传递地址交换,因为形参的改变不改变实参
void swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}
删除数据
-
删除数据其实是删除堆顶的数据,由于堆是由一个数组来存放数据的,那么我们该如何删除堆顶(数组的第一个元素数据)的数据呢?
-
这里我们将堆顶数据和数组的最后一个数据交换一下,然后
size减一,就实现了删除。 -
当然,删除过后,此时的堆已经不再是堆了,所以我们需要对新的堆顶数据执行一下向下调整算法,图示:

-
对于向下调整算法,我们先要找到该结点(假设下标为
parent)的孩子结点,而孩子结点又分为左孩子结点(下标为parent * 2 + 1)和右孩子结点(下标为parent * 2 + 2),所以我们需要找出两个孩子结点当中较大的那个,如果该节点的数据比较大的那个孩子结点的数据要小,那就进行交换,然后循环往复继续向下寻找孩子结点重整堆。 -
整个操作,我们可以先比较两个孩子的大小找出大的那个,然后在与大的这个孩子结点进行比较,如果父结点比他小(以大堆为例),说明这个孩子结点该上位了。然后继续向下执行这个操作。
相关函数接口功能的实现:
// 删除数据,删除堆顶的数据
void HeapPop(Heap* php)
{// 判断php的合法性并且要保证堆不为空,空就不能删了assert(php && !HeapEmpty(php));// 将堆的第一个数据与堆的最后一个数据交换swap(&php->a[0], &php->a[php->size - 1]);// size减一表示删除最后一个数据php->size--;// 对新的堆顶执行向下调整算法adjustdown(php->a, php->size, 0);
}
向下调整算法:
// 向下调整
void adjustdown(HPDataType* a, int size, int parent)
{// 先假设大的那个孩子结点为左孩子结点int child = parent * 2 + 1;while (child < size) // 如果child小于此时数组的长度就继续{// 第一个判断是防止没有右孩子结点的情况// 第二个判断是如果右孩子存在并且右孩子结点的数据大于左孩子结点的数据,就child加一指向右孩子结点if (child + 1 < size && a[child + 1] > a[child]) child++;// 如果父节点数据小于child结点数据,就交换重整堆if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else break; // 如果父节点数据大于child结点数据,说明堆已经调整完毕,直接跳出循环不在调整}
}
堆的数据个数
- 由于我们定义了一个变量来统计堆的数据个数,所以在这里只需要返回那个变量的值即可。
相关函数接口功能的实现:
// 获取堆数据个数
int HeapSize(Heap* php)
{assert(php);return php->size;
}
获取堆顶数据
-
获取堆顶数据就是数组的第一个元素。
-
如果此时堆为空,就不能获取了。
相关函数接口功能的实现:
// 获取堆顶数据
HPDataType HeapTop(Heap* php)
{assert(php && !HeapEmpty(php));return php->a[0];
}
用数组创建堆
-
用数组创建堆就是将一个数组里面的所有元素拷贝到堆的数组里,然后进行建堆。
-
我们首先开辟一个堆空间(就是一段连续的数组),长度与给的数组的长度相同,然后将给的数组里的元素拷贝过来,最后将堆里面的数据进行建堆。
-
如何建堆?我们从最后一个结点的父节点开始,依次执行向下调整算法,直到根节点执行完全后,便建成了堆。当然我们也可以从第二个结点开始,依次执行向上调整算法,直到最后一个结点执行完后便建成了堆,不过这样的时间复杂度为
O(n * logn),而前面的向下调整算法的方式的时间复杂度为O(n),所以这里我们采用向下调整算法的方式来建堆。至于这两个调整算法的时间复杂度是如何计算出来的,这里就不做讨论,它的本质其实是有关数列求和的计算。
向下调整算法方式建堆图示:


- 有了上面的思路,接下来就是代码实现了。
相关函数接口功能的实现:
// 数组创建堆
void HeapCreateArray(Heap* php, HPDataType* a, int n)
{// php不能为NULL,a不能为NULLassert(php && a);// 开辟可存放n个数据的堆空间php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){perror("malloc fail");exit(-1);}// 拷贝数据memcpy(php->a, a, sizeof(HPDataType) * n);php->size = php->capacity = n;// 从最后一个结点的父节点开始依次执行向下调整算法,直到根结点执行完后结束// 这里i为什么初始化 (n - 2) / 2 呢? 其实就是最后一个结点的父节点的下标// 前面说了,寻找父节点的下标是 (child - 1) / 2// 这里是寻找最后一个结点的父结点,而最后一个结点的下标是 (n - 1)(n是数组长度)// 所以它的父节点就是 (n - 1 - 1) / 2 , 也就是(n - 2) / 2for (int i = (n - 2) / 2; i >= 0; i--) adjustdown(php->a, n, i);
}
对数组堆排序
-
有了建堆的认识,堆排序也不难,只不过需要注意几个细节。
-
对数组排序,首先就是要对这个数组建堆,如果是要将数组升序,就建为大堆,如果是要将数组降序,就建为小堆,为什么呢?这里以升序为例进行讲解,弄懂了升序,降序也只是大于小于号的问题了。
-
当数组建成大堆形式后(同样的,使用向下调整算法建堆),堆顶元素是最大的,此时我们可以将堆顶元素与最后一个元素进行交换,这样最大的元素就到了数组的末尾了。然后我们对这个处在数组最后一个位置的最大元素视而不见,将交换过去的堆顶元素执行向下调整算法,这时,第二大的元素就到了堆顶,然后此时的堆顶元素继续与最后一个元素进行交换 (注意第一个交换过去的最大的元素已经不在范围内了,也就是说每将一个当前最大的数交换过去后,可视作
size减一一次) ,然后再将交换过去的堆顶元素执行向下调整算法…这样循环往复,最终该数组就变成了升序。
相关函数接口功能的实现:
// 堆排序
void HeapSort(HPDataType* a, int n)
{assert(a);// 向下调整, 这里是建大堆for (int i = (n - 2) / 2; i >= 0; i--) adjustdown(a, n, i);// 排序(建的大堆就是升序)int k = n - 1;while (k > 0){swap(&a[0], &a[k]);adjustdown(a, k, 0);k--;}
}
有关topk问题
-
如何在百万个成绩数据里面找出前十个最好的?这就是典型的
topk问题。可以看到,它需要处理的数据非常多(当然也有的很少,不过面试一般就是问多的情况,让你找出前k个最那啥的),因此这里需要用到堆来解决。 -
为什么堆可以解决呢?堆的堆顶要么是整个堆里最大的元素,要么是整个堆里最小的元素。根据这一性质,假如求很多数据中前
k个最小的数据,我们可以先开辟一个堆空间,该堆空间可以存放k个数据,然后我们将很多数据中的前k个数据拷贝进堆里,并将其建成大堆,此时堆的堆顶元素就是堆里所有元素最大的那一个,接着,我们从很多数据的第k个数开始,遍历这些数据,如果该数据小于此时堆顶的数据,就将堆顶数据更新为这个小的数据,然后对其执行向下调整算法,执行完过后,堆顶还是堆中最大的那个元素,就这样判断并操作,直到遍历结束,堆中就是那前k个最小的数啦。最后将这些数打印即可。(找前k个最小的数就是建大堆,反之,建小堆,这里就不作讨论了) -
原理(以求前
k个最小的数为例):每次比堆顶小的元素入堆并调整后,之前堆中最大的元素被抛弃,新的最大的元素上位了,这样循环往复下去,每次操作除大的进小的,当然最后堆中就是前k个最小的数啦。
相关函数接口功能的实现:
// topk问题
void PrintTopK(HPDataType* a, int n, int k)
{assert(a);// 开辟能够存放k个数据的堆空间HPDataType* topk = (HPDataType*)malloc(sizeof(HPDataType) * k);if (topk == NULL){perror("malloc fail");exit(-1);}// 拷贝前k个数据进堆memcpy(topk, a, sizeof(HPDataType) * k);// 找前k个最小的,建大堆for (int i = (k - 2) / 2; i >= 0; i--) adjustdown(topk, k, i);// 对topk堆进行 除大的进小的 操作for (int i = k; i < n; i++){if (a[i] < topk[0]){topk[0] = a[i];// 每次进来一个较小的元素都要执行一遍向下调整算法来调整堆adjustdown(topk, k, 0);}}// 打印 topkfor (int i = 0; i < k; i++) printf("%d ", topk[i]);// 最后使用完堆后记得释放free(topk);
}
整体代码展示
heap.h
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;// 以大堆为例
// 堆初始化
void HeapInit(Heap* php);
// 数组创建堆
void HeapCreateArray(Heap* php, HPDataType* a, int n);// 插入数据
void HeapPush(Heap* php, HPDataType x);
// 删除数据
void HeapPop(Heap* php);// 获取堆顶数据
HPDataType HeapTop(Heap* php);// 获取堆数据个数
int HeapSize(Heap* php);// 堆判空
bool HeapEmpty(Heap* php);// 堆的销毁
void HeapDestroy(Heap* php);// 交换
void swap(HPDataType* a, HPDataType* b);
// 向上调整
void adjustup(HPDataType* a, int child);
// 向下调整
void adjustdown(HPDataType* a, int size, int parent);// 堆排序
void HeapSort(HPDataType* a, int n);
// topk问题
void PrintTopK(HPDataType* a, int n, int k);
heap.c
#include "heap.h"// 堆初始化
void HeapInit(Heap* php)
{assert(php);php->a = NULL;php->capacity = php->size = 0;
}
// 数组创建堆
void HeapCreateArray(Heap* php, HPDataType* a, int n)
{assert(php && a);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){perror("malloc fail");exit(-1);}memcpy(php->a, a, sizeof(HPDataType) * n);php->size = php->capacity = n;for (int i = (n - 2) / 2; i >= 0; i--) adjustdown(php->a, n, i);
}// 插入数据
void HeapPush(Heap* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size++] = x;adjustup(php->a, php->size - 1);
}
// 删除数据,删除堆顶的数据
void HeapPop(Heap* php)
{assert(php && !HeapEmpty(php));swap(&php->a[0], &php->a[php->size - 1]);php->size--;adjustdown(php->a, php->size, 0);
}// 获取堆顶数据
HPDataType HeapTop(Heap* php)
{assert(php && !HeapEmpty(php));return php->a[0];
}// 获取堆数据个数
int HeapSize(Heap* php)
{assert(php);return php->size;
}// 堆判空
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}// 堆的销毁
void HeapDestroy(Heap* php)
{assert(php);free(php->a);php->capacity = php->size = 0;
}// 交换
void swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}
// 向上调整
void adjustup(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else break;}
}
// 向下调整
void adjustdown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child + 1] > a[child]) child++;if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else break;}
}// 堆排序
void HeapSort(HPDataType* a, int n)
{assert(a);// 向下调整, 这里是建大堆for (int i = (n - 2) / 2; i >= 0; i--) adjustdown(a, n, i);// 排序(建的大堆就是升序)int k = n - 1;while (k > 0){swap(&a[0], &a[k]);adjustdown(a, k, 0);k--;}
}// topk问题
void PrintTopK(HPDataType* a, int n, int k)
{assert(a);HPDataType* topk = (HPDataType*)malloc(sizeof(HPDataType) * k);if (topk == NULL){perror("malloc fail");exit(-1);}memcpy(topk, a, sizeof(HPDataType) * k);// 找前k个最小的,建大堆for (int i = (k - 2) / 2; i >= 0; i--) adjustdown(topk, k, i);for (int i = k; i < n; i++){if (a[i] < topk[0]){topk[0] = a[i];adjustdown(topk, k, 0);}}for (int i = 0; i < k; i++) printf("%d ", topk[i]);free(topk);
}
test.c
#include "heap.h"void test1()
{Heap hp;HeapInit(&hp);HeapPush(&hp, 22);HeapPush(&hp, 122);HeapPush(&hp, 16);HeapPush(&hp, 45);HeapPush(&hp, 56);HeapPush(&hp, 18);HeapPush(&hp, 134);HeapPush(&hp, 99);HeapDestroy(&hp);
}void test2()
{Heap hp;HeapInit(&hp);int arr[] = { 34,113,78,44,98,99,35,26,18,68 };int n = sizeof(arr) / sizeof(arr[0]);HeapCreateArray(&hp, arr, n);while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");HeapDestroy(&hp);
}void test3()
{int arr[] = { 34,113,78,44,98,99,35,26,18,68 };int n = sizeof(arr) / sizeof(arr[0]);HeapSort(arr, n);for (int i = 0; i < n; i++) printf("%d ", arr[i]);printf("\n");
}void testTopK()
{int arr[] = { 34,113,78,44,98,99,35,26,18,68 };int n = sizeof(arr) / sizeof(arr[0]);PrintTopK(arr, n, 5);
}int main()
{//test1();test2();test3();testTopK();return 0;
}
写在最后
💝
❤️🔥后续将会持续输出有关数据结构与算法的文章,你们的支持就是我写作的最大动力!
感谢阅读本小白的博客,错误的地方请严厉指出噢~
相关文章:

【数据结构】堆
文章目录前言堆的概念及结构堆初始化堆的判空堆的销毁插入数据删除数据堆的数据个数获取堆顶数据用数组创建堆对数组堆排序有关topk问题整体代码展示写在最后前言 🚩前面了解了树(-> 传送门 <-)的概念后,本章带大家来实现一…...
电脑硬盘文件数据误删除/格式化为什么可以恢复? 怎么恢复?谈谈文件删除与恢复背后的原理
Hello 大家好, 我是元存储~ 主页:元存储的博客_CSDN博客 1. 硬盘数据丢失场景 我们在每天办公还是记录数据的时候,文件存储大多数都是通过硬盘进行存储的,因此,使用多了,各种问题就会出现,比如…...
Gateway服务网关
Spring Cloud Gateway为微服务架构提供一种简单有效的统一的 API 路由管理方式。Gateway网关是所有微服务的统一入口。网关的核心功能特性:请求路由和负载均衡:一切请求都必须先经过gateway,但网关不处理业务,而是根据某种规则&am…...
K8S + GitLab + Jenkins自动化发布项目实践(一)
K8S GitLab Jenkins自动化发布项目实践(一)发布流程设计安装Docker服务部署Harbor作为镜像仓库部署GitLab作为代码仓库常用Git命令发布流程设计 #mermaid-svg-pe9VmFytb9GmqMvG {font-family:"trebuchet ms",verdana,arial,sans-serif;font-…...

【数据结构篇C++实现】- 堆
文章目录🚀一、堆的原理精讲⛳(一)堆的概念⛳(二)看图识最大堆⛳(三)详解堆是用数组表示的树🚀二、堆的向下调整算法🚀三、堆的向上调整算法🚀四、将任意一棵…...

C++笔试题
作用域运算符(::)的作用:1.存在具有相同名称的局部变量时,访问全局变量。2.在类之外定义类相关函数。3.访问类的静态变量。4.在多重继承的情况下,如果两个基类中存在相同的变量名,可以使用作用域运算符来进行区分。5.限定成员函数…...

【Python】基本语法
数据类型 通过 print(type(x)) 可以输出 x 的数据类型,type() 函数可以获取数据类型 整数 a 10 print(type(a)) 浮点数 a 0.5 print(type(a)) 字符串 a hello print(type(a)) 获取字符串长度 a hello print(len(a))字符串拼接 a hello b world prin…...
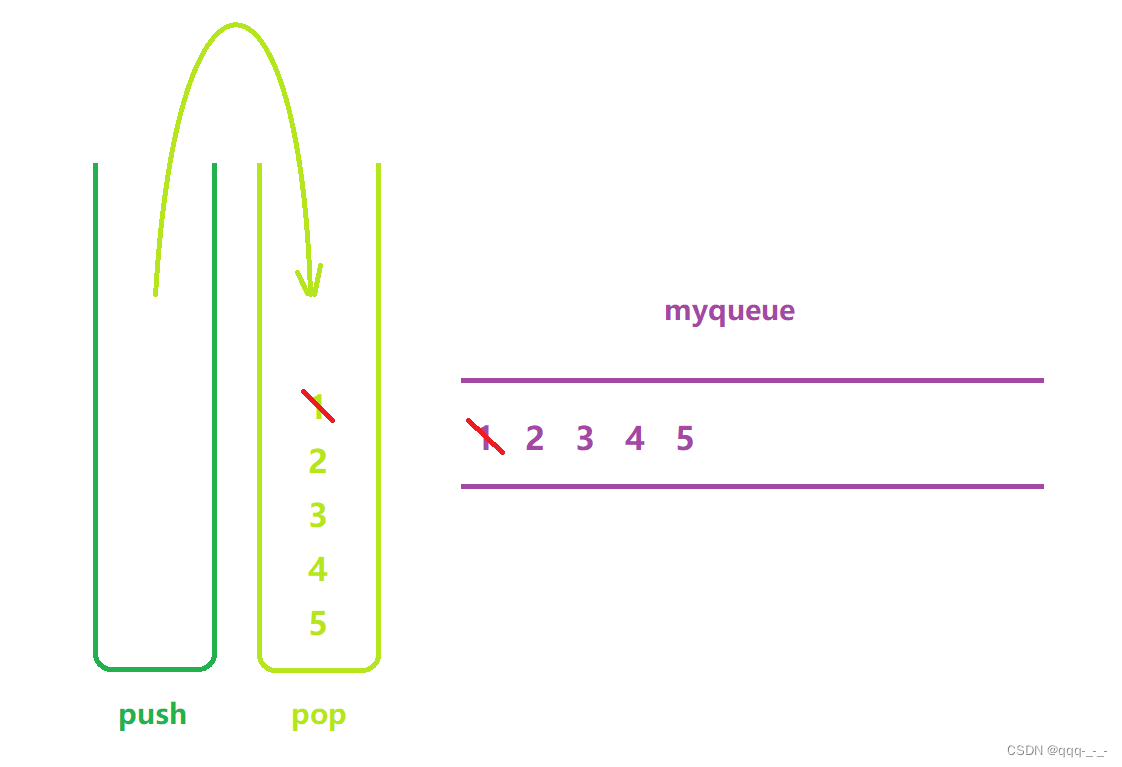
用栈实现队列(图示超详解哦)
全文目录引言用栈实现队列题目介绍思路简述实现栈的部分队列的部分创建队列判断队列是否为空在队列尾入在队列头出访问队头元素释放队列总结引言 在上一篇文章中,我们了解了用两个队列实现栈。在这篇问章中将继续介绍用两个栈实现队列的OJ练习: 用栈实现…...

Spring - Spring 注解相关面试题总结
文章目录01. Spring 配置方式有几种?02. Spring 如何实现基于xml的配置方式?03. Spring 如何实现基于注解的配置?04. Spring 如何基于注解配置bean的作用范围?05. Spring Component, Controller, Repository, Service 注解有何区别…...
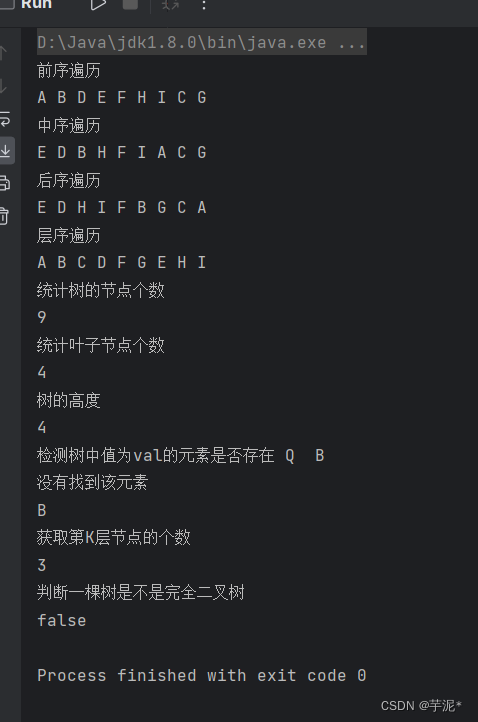
【数据结构】实现二叉树的基本操作
目录 1. 二叉树的基本操作 2. 具体实现 2.1 创建BinaryTree类以及简单创建一棵树 2.2 前序遍历 2.3 中序遍历 2.4 后序遍历 2.5 层序遍历 2.6 获取树中节点的个数 2.7 获取叶子节点的个数 2.8 获取第K层节点的个数 2.9 获取二叉树的高度 2.10 检测值为val的元素是否…...
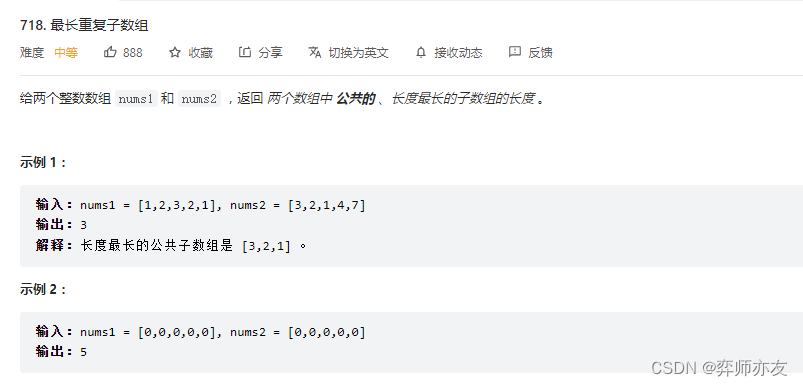
代码随想录算法训练营第五十二天| ● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列 看完题后的思路 dp[i] [0,i]子数组中,以nums[i]结尾的子序列的长度 dp[i]dp[j]1 j从i-1向0遍历,在所有nums[j]<nums[i]中dp[j]最大 初始化 dp[0]1 代码 class Solution {public int lengthOfLIS(int[] nums) {if (nums.length0){return 0;}int[] dpne…...

手机验证发送及其验证(基于springboot+redis)保姆级
在Java开发中,发送手机验证码时需要考虑以下几个问题: 验证码的有效期:验证码应该有一定的有效期,一般设置为几分钟或者十几分钟。过期的验证码应该被认为是无效的,不能用于验证用户身份。手机号码格式的校验…...

【JavaScript 逆向】数美滑块逆向分析
声明本文章中所有内容仅供学习交流,相关链接做了脱敏处理,若有侵权,请联系我立即删除!案例目标验证码:aHR0cHM6Ly93d3cuaXNodW1laS5jb20vbmV3L3Byb2R1Y3QvdHcvY29kZQ以上均做了脱敏处理,Base64 编码及解码方…...

多任务之线程
文章目录一、多任务是什么?二、多任务-线程四、通过继承Tread类完成创建线程五、资源竞争六、同步与互斥锁七、对峙与避免死锁一、多任务是什么? 多个函数同时执行一件事情就是多任务,没有多任务的时候任务执行都是按照顺序的,而…...
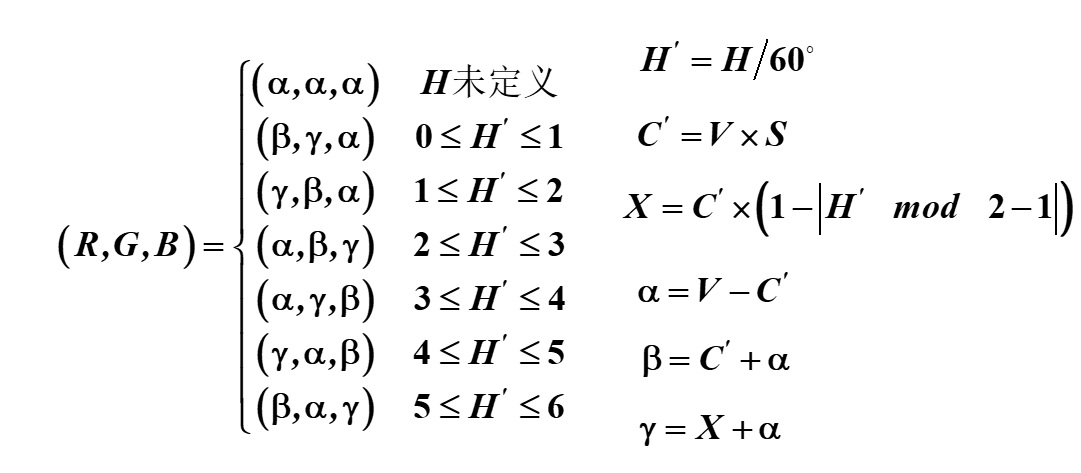
(数字图像处理MATLAB+Python)第二章数字图像处理基础-第二节:色度学基础与颜色模型
文章目录一:颜色匹配二:CIE 1931-RGB系统三:CIE 1931标准色度系统四:CIE 1976Lab均匀颜色空间五:孟塞尔表色系统(1)孟塞尔明度(Value,记为V)(2)孟塞尔彩度(Ch…...
)
【华为OD机试 2023最新 】 网上商城优惠活动(C++)
文章目录 题目描述输入描述输出描述备注用例题目解析C++题目描述 某网上商场举办优惠活动,发布了满减、打折、无门槛3种优惠券,分别为: 每满100元优惠10元,无使用数限制,如100199元可以使用1张减10元,200299可使用2张减20元,以此类推;92折券,1次限使用1张,如100元,…...

记一次CentOS 8 部署packstack部署OpenStack失败案例,请直接看最后
首先你需要一台安装好CentOS8 的虚拟机,相关参数如图。两块网卡,网卡1 NAT IP 192.168.100.100 GW192.168.100.2 网卡2 可不做配置。能ping通百度。创建完成虚拟机记得打好快照。 开机编辑基本配置环境变量 [rootlocalhost ~]# nmcli connection show NA…...

【2023春招】美团技术岗笔试10min+AK
随手投递了前端&移动端,笔试2道算法+选择+行测题(为什么笔试会有行测题?) 目录 T1-火车栈结构 题意 输入描述 输出描述 样例 AC_Code T2-春游...

Echarts实现图表自适应屏幕分辨率
一:简介 之前做项目的时候要实现echarts图表随浏览器窗口大小变化而改变,echarts本身提供了一个resize()方法,然后我们需要用一个函数实现浏览器窗口监听,最初我选用的是window.onresize方法,当页面只有一个图表时可以…...

【2023年第十一届泰迪杯数据挖掘挑战赛】B题:产品订单的数据分析与需求预测 建模及python代码详解 问题一
相关链接 【2023年第十一届泰迪杯数据挖掘挑战赛】B题:产品订单的数据分析与需求预测 建模及python代码详解 问题一 【2023年第十一届泰迪杯数据挖掘挑战赛】B题:产品订单的数据分析与需求预测 建模及python代码详解 问题二 1 题目 一.问题…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...