蓝桥杯冲刺 - week2
文章目录
- 💬前言
- 🌲day1
- 最大和 (DP+质因数分解)
- 901. 滑雪 - 记忆化搜索
- 🌲day2
- 1227. 分巧克力 - 二分
- 🌲day3
- 1221. 四平方和 - 空间换时间
- 1230. K倍区间
- 🌲day4
- 1076. 迷宫问题 - 路径
- 2017-迷宫-填空
- 🌲day5
- 848. 有向图的拓扑序列
- 🌲day6
- 进制转换+扫描线算法(二维区间合并面积和)
- 🌲day7
- 蓝桥杯C/C++B组历届真题-精选填空专项
💬前言
🚩重难点突破,重在场景应用,以真题带练,涉及算法标签[⚽️DP,⚽️二分,⚽️图论,⚽️前缀和,⚽️进制转换,⚽️扫描线]
在理解DFS,DP的基础上进一步巩固知识点,结合题目变化运用,加深记忆和理解
⏳最后三个星期大家一起冲刺,祝大家rp++🏅
如果对您有帮助的话还请动动小手 点赞👍,收藏⭐️,关注❤️
🌲day1
最大和 (DP+质因数分解)
问题描述
小蓝在玩一个寻宝游戏, 游戏在一条笔直的道路上进行, 道路被分成了 n 个方格, 依次编号 1 至 n, 每个方格上都有一个宝物, 宝物的分值是一个整数 (包括正数、负数和零), 当进入一个方格时即获得方格中宝物的分值。小蓝可 以获得的总分值是他从方格中获得的分值之和。
小蓝开始时站在方格 1 上并获得了方格 1 上宝物的分值, 他要经过若干步 到达方格n。
当小蓝站在方格 p 上时, 他可以选择跳到 p+1 到 p+D(n-p) 这些方格 中的一个, 其中 D(1)=1, D(x)(x>1)D(1)=1定义为 x 的最小质因数。
给定每个方格中宝物的分值, 请问小蓝能获得的最大总分值是多少。
输入格式
输入的第一行包含一个正整数 n。
第二行包含 n 个整数, 依次表示每个方格中宝物的分值。
输出格式
输出一行包含一个整数, 表示答案。
样例输入
51 -2 -1 3 5
样例输出
8
样例输出
最优的跳跃方案为: 1→3→4→5。1 \rightarrow 3 \rightarrow 4 \rightarrow 5 。1→3→4→5。
评测用例规模与约定
对于 40 %40 的评测用例, 1≤n≤100。1 \leq n \leq 100 。1≤n≤100。
对于 80 %80 的评测用例, 1≤n≤1000。1 \leq n \leq 1000 。1≤n≤1000。
对于所有评测用例, 1≤n≤100001 \leq n \leq 100001≤n≤10000, 每个宝物的分值为绝对值不超过 10510^5105
的整数。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;int n;
long long dp[10005];
long long w[10005];bool is_prime(int x)
{if(x < 2) return false;for (int i = 2; i < x / i; ++ i )if (x % i == 0)return false;return true;
}int get(int x) //x的最小质因数
{for(int i = 2; i <= x / i; i++)if(x % i == 0 && is_prime(i)) return i;if(x > 1) return x;
}int main()
{cin >> n;for (int i = 1; i <= n; i++)//输入结点权值{scanf("%lld", &w[i]); dp[i] = INT_MIN;}dp[1] = w[1]; for (int i = 1; i <= n; i++) //选择任意起点{int len = i + get(n - i);for (int j = i + 1; j <= len; j++) //[p+1, p + (n-p的最小质因数)]遍历所有下一步跳跃转移 - dp[]_max_value{dp[j] = max(dp[j], dp[i] + w[j]);}}cout << dp[n];return 0;
}
901. 滑雪 - 记忆化搜索
给定一个 R 行 C 列的矩阵,表示一个矩形网格滑雪场。
矩阵中第 i 行第 j 列的点表示滑雪场的第 i 行第 j 列区域的高度。
一个人从滑雪场中的某个区域内出发,每次可以向上下左右任意一个方向滑动一个单位距离。
当然,一个人能够滑动到某相邻区域的前提是该区域的高度低于自己目前所在区域的高度。
下面给出一个矩阵作为例子:
1 2 3 4 516 17 18 19 615 24 25 20 714 23 22 21 813 12 11 10 9
在给定矩阵中,一条可行的滑行轨迹为 24−17−2−1。
在给定矩阵中,最长的滑行轨迹为 25−24−23−…−3−2−1,沿途共经过 25 个区域。
现在给定你一个二维矩阵表示滑雪场各区域的高度,请你找出在该滑雪场中能够完成的最长滑雪轨迹,并输出其长度(可经过最大区域数)。
输入格式
第一行包含两个整数 R 和 C。
接下来 R 行,每行包含 C 个整数,表示完整的二维矩阵。
输出格式
输出一个整数,表示可完成的最长滑雪长度。
数据范围
1≤R,C≤300,
0≤矩阵中整数≤10000
输入样例:
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
输出样例:
25
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 310;int n, m;
int g[N][N];
int f[N][N];int dx[] = {-1, 0 , 1, 0}, dy[] = {0, 1, 0, -1};int dp(int x, int y)
{int &v = f[x][y];if(v != -1) return v;v = 1;for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a >= 1 && a <= n && b >= 1 && b <= m && g[a][b] < g[x][y])v = max(v, dp(a, b) + 1); }return v;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) for (int j = 1; j <= m; j ++ )scanf("%d", &g[i][j]);memset(f, -1, sizeof f);int res = 0;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)res = max(res, dp(i, j));printf("%d\n", res);return 0;
}
🌲day2
1227. 分巧克力 - 二分
儿童节那天有 K 位小朋友到小明家做客。
小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。
切出的巧克力需要满足:
形状是正方形,边长是整数大小相同
例如一块 6×5 的巧克力可以切出 6 块 2×2 的巧克力或者 2 块 3×3 的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少么?
输入格式
第一行包含两个整数 N 和 K
以下 N 行每行包含两个整数 Hi 和 Wi。
输入保证每位小朋友至少能获得一块 1×1
的巧克力。
输出格式
输出切出的正方形巧克力最大可能的边长。
数据范围
1≤N,K≤10510^5105
,
1≤Hi,Wi≤10510^5105
输入样例:
2 10
6 5
5 6
输出样例:
2
首先判断单调性【随着选取切除的边长越大切出的块数越少:单调递减==>可以二分】
边长x, 切出的块数res(需满足res >= k) 边长为x最多切的块数为: ⌊wx⌋∗⌊hx⌋\lfloor \frac{w}{x} \rfloor * \lfloor \frac{h}{x} \rfloor⌊xw⌋∗⌊xh⌋ (向下取整)
#include <bits/stdc++.h>using namespace std;const int N = 100010;int n, k;
int h[N], w[N];bool check(int mid) //判断边长mid能否切k块
{int res = 0;//边长为mid时能切的块数resfor (int i = 0; i < n; i ++ )//共n块巧克力来切{res += (h[i] / mid) * (w[i] / mid);// (向下取整) (长 / 划分的边长mid) * (宽 / 划分的边长mid) [小学划分easy]if (res >= k) return true;//能切k块}return false;
}int main()
{scanf("%d%d", &n, &k);for (int i = 0; i < n; i ++ ) scanf("%d%d", &h[i], &w[i]);int l = 1, r = 1e5;//边长至少1 * 1 ,左边界L从1开始, 且右边界R不超过W或H (长宽) while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;//边长为mid能切k块,往更大的尝试,找最大else r = mid - 1;//mid不满足,则在试试[1,mid - 1] 找满足的}printf("%d\n", r);return 0;
}
🌲day3
1221. 四平方和 - 空间换时间
四平方和定理,又称为拉格朗日定理:
每个正整数都可以表示为至多 4 个正整数的平方和。
如果把 0 包括进去,就正好可以表示为 4 个数的平方和。
比如:
5=02+02+12+225=0^2+0^2+1^2+2^25=02+02+12+22
7=12+12+12+227=1^2+1^2+1^2+2^27=12+12+12+22
对于一个给定的正整数,可能存在多种平方和的表示法。
要求你对 4 个数排序:
0≤a≤b≤c≤d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法。
输入格式
输入一个正整数 N。
输出格式
输出4个非负整数,按从小到大排序,中间用空格分开。
数据范围
0<N<5×1060<N<5\times10^60<N<5×106
输入样例:
5
输出样例:
0 0 1 2
算法思想:
先枚举c2+d2c^2 + d^2c2+d2的所有值存入数组, 令sum = n - c2+d2c^2 + d^2c2+d2, 枚举a2+b2a^2 + b^2a2+b2过程中判断是否出现在标记数组中
【是否C[sum](或D[sum])被标记】, 输出ans{a, b, C[sum], D[sum]};
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 5e6 + 10;int n;int C[N], D[N]; //存c与d的平方和为下标sum, c = C[sum],d = D[sum] int main()
{cin >> n;memset(C, -1, sizeof C); //初始标记for (int c = 0; c * c <= n; c ++ ) // 存一对for (int d = c; c * c + d * d <= n; d ++ ){int sum = c * c + d * d;if (C[sum] == -1) //存第一次出现的-满足最小C[sum] = c, D[sum] = d; //hash表<sum,对应组成c> , <sum,对应组成d>}for (int a = 0; a * a <= n; a ++ )for (int b = a; a * a + b * b <= n; b ++ ){int sum = n - a * a - b * b; //剩余差值if (C[sum] != -1){ //查找存放值中是否存在剩余差值printf("%d %d %d %d\n", a, b, C[sum], D[sum]);return 0;}}return 0;
}
#include<bits/stdc++.h>using namespace std;const int N=2500010;int n;int main()
{cin >> n;for(int a = 0; a * a <= n; a++){for(int b = a; a * a + b * b <= n; b++){for(int c = b; c * c + b * b + a * a <= n; c++){int t = n - a * a - b * b - c * c;int d = sqrt(t);if(d * d == t){printf("%d %d %d %d", a, b, c, d);return 0;}}}}
}
1230. K倍区间
给定一个长度为 N 的数列,A1,A2,…AN,如果其中一段连续的子序列 Ai,Ai+1,…Aj 之和是 K 的倍数,我们就称这个区间 [i,j] 是 K 倍区间。
你能求出数列中总共有多少个 K 倍区间吗?
输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行包含一个整数 Ai。
输出格式
输出一个整数,代表 K 倍区间的数目。
数据范围
1≤N,K≤100000,
1≤Ai≤100000
输入样例:
5 2
1
2
3
4
5
输出样例:
6
前缀和优化 + 区间差值==k倍数(常用等效法) + 余数组合:
题意:以i为右端点的区间, (s[i] - s[i - 1] ~ s[i] - s[0] ) 有多少个区间值 % k == 0
k倍区间转化成s[i] - s[j] % k == 0 <==> s[j] % k == s[i] % k 余数是否相等【相等说明这一段的数的和是k的倍数】
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;const int N = 100010;int n, k;//从n个数中找区间为k的倍数
LL s[N], cnt[N];//cnt[x]:动态统计余数为x的数量int main()
{scanf("%d%d", &n, &k);for (int i = 1; i <= n; i ++ )//构造前缀和{scanf("%lld", &s[i]);s[i] += s[i - 1];}LL res = 0;cnt[0] = 1;//一个都不选,则余数为0,初始有1个 for (int i = 1; i <= n; i ++ ){ res += cnt[s[i] % k]; //当前余数 与之前[0,i-1]段中相同余数的可组合构成一段k倍数的区间cnt[s[i] % k] ++ ;//当前余数的数量 ++}printf("%lld\n", res);return 0;
}
先全部统计 - 相同余数的做左右端点可组合成k倍区间:组合数Cn2C_n^2Cn2
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long LL;const int N = 1e5 + 10;LL s[N], cnt[N];int n, k;int main()
{scanf("%d%d", &n, &k);for (int i = 1; i <= n; i ++ )//构造前缀和{scanf("%lld", &s[i]);s[i] += s[i - 1];}cnt[0] = 1; //若不令cnt[0]=1, 则统计完res += cnt[0] :余数0可以仅选一个点构成s[i] - s[1]段k倍区间for (int i = 1; i <= n; i ++ ) cnt[s[i] % k] ++; //统计余数LL res = 0;for (int i = 0; i < k; i ++ ) //枚举余数res += (LL) cnt[i] * (cnt[i] - 1) / 2; //组合数printf("%lld\n", res);return 0;
}
🌲day4
1076. 迷宫问题 - 路径
2017-迷宫-填空
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
下图给出了一个迷宫的平面图,其中标记为 11 的为障碍,标记为 00 的为可以通行的地方。
010000
000100
001001
110000
迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这 个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按 DRRURRDDDR 的顺序通过迷宫, 一共 1010 步。其中 D、U、L、RD、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫(3030 行 5050 列),请找出一种通过迷宫的方式,其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中 D<L<R<UD<L<R<U。
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 55;int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};int n = 30, m = 50;
char g[N][N];
int dist[N][N];
PII pre[N][N];
char c[N][N]; //存字符char get(int k) //转换成方向字符
{if (k == 0)return 'D';if (k == 1)return 'L';if (k == 2)return 'R';return 'U';
}void bfs()
{queue<PII> q;q.push({0, 0});g[0][0] = '1';while (q.size()){auto t = q.front();q.pop();for (int i = 0; i < 4; ++ i ){int tx = t.x + dx[i], ty = t.y + dy[i];if (tx < 0 || ty < 0 || tx >= n || ty >= m || g[tx][ty] == '1') continue;dist[tx][ty] = dist[t.x][t.y] + 1;g[tx][ty] = '1';pre[tx][ty] = t; //存从[t.x][t.y]走到的下一步{a, b}的路径q.push({tx, ty});c[tx][ty] = get(i); //}}
}int main()
{for (int i = 0; i < n; ++ i )cin >> g[i];bfs();PII t = {n - 1, m - 1};string res;while (t.x != 0 || t.y != 0) //逆回到起点{res += c[t.x][t.y]; //从终点->起点t = pre[t.x][t.y];}reverse(res.begin(), res.end()); //起点->终点cout << res << endl;return 0;
}
答案
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
🌲day5
848. 有向图的拓扑序列
给定一个 n 个点 m 条边的有向图,点的编号是 1 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 x 和 y,表示存在一条从点 x 到点 y 的有向边 (x,y)。
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1。
数据范围
1≤n,m≤10510^5105
输入样例:
3 3
1 2
2 3
1 3
输出样例:
1 2 3
图中点之间的最短距离 - BFS
邻接表知识总结
具体含义理解
h[a] : 存点a邻接边(可能多个idx,头结点存放最后一次添加到a的边 )
e[idx] : 存第idx条边的终点(从h[a]遍历取的边即为 a -> e[idx] )
ne[idx]: 此边的起点h[] (头插法中第idx条边: ne[idx] -> e[idx]);
idx : 边的编号
w[idx]: 存第idx条边的边权
add(a, b, c) : 头插法第idx条边a->b边权为c
#include<cstdio>
#include<cstring>using namespace std;const int N = 1e5 + 10;int n, m;
int h[N], e[N], ne[N], idx; //【注意邻接表初始化h[]头结点数组 = -1 : 表示null】
int q[N], d[N];void add(int a, int b) //a -> b【h[a]头插入点b】
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int bfs()
{int hh = 0, tt = -1;q[++ tt] = 1; //从第1个结点出发[第一个结点入队]memset(d, -1, sizeof d);d[1] = 0;while(hh <= tt) {auto t = q[hh ++]; //取队头 + 出队for(int i = h[t]; i != -1; i = ne[i]) //h[t]开头的链表遍历 { int j = e[i]; //【判断当前点下标i对应边的另一端点是否走过:能否从i = idx走到另一端点(下标e[i])】if(d[j] == -1) //未访问过 (不能用~d[j] 【如d[j] = 1,但是取反!= 0:即访问过也会遍历-SF段错误】){d[j] = d[t] + 1;//统计步数q[++ tt] = j; //入队}}}return d[n]; //返回到第n个节点的步数
}int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof h); //注意初始化头结点 = -1 :表示nullfor(int i = 0; i < m; i++){int a, b;scanf("%d%d", &a, &b);add(a, b);}printf("%d\n", bfs());return 0;
}
🌲day6
进制转换+扫描线算法(二维区间合并面积和)
🌲day7
蓝桥杯C/C++B组历届真题-精选填空专项
相关文章:

蓝桥杯冲刺 - week2
文章目录💬前言🌲day1最大和 (DP质因数分解)901. 滑雪 - 记忆化搜索🌲day21227. 分巧克力 - 二分🌲day31221. 四平方和 - 空间换时间1230. K倍区间🌲day41076. 迷宫问题 - 路径2017-迷宫-填空🌲day5848. 有…...
第十四届蓝桥杯三月真题刷题训练——第 20 天
目录 第 1 题:纸张尺寸 问题描述 输入格式 输出格式 样例输入1 样例输出1 样例输入 2 样例输出 2 运行限制 代码: 解析: 第 2 题:最大数字 第 3 题:全排列的价值_递推公式 问题描述 输入格式 输出格式…...
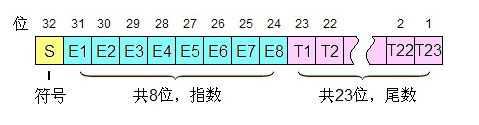
【C++】科普:C++中的浮点数怎么在计算机中表示?
这里我们以8.25这个数为例说明计算机时如何存取float类型的数据的: float a 8.25;引言 1. 所占位数 首先,明确一个概念,float类型的数据在常规计算机中通常占4个字节,也就是32位。其内存分布如图: 位字段说明所占位…...

Linux 多线程:多线程和多进程的对比
目录一、多进程优缺点二、多线程优缺点三、使用多执行流的场景在多任务处理中,我们既可以使用多进程,也可以使用多线程。但多进程和多线程并不是随意选择的,因为它们应对的场景不同,优缺点也不同。 一、多进程优缺点 多进程就是在…...
IO流你了解多少
IO流你了解多少 🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目前在某公…...

【C++】C++ 11 新特性之auto关键字
文章目录类型别名的思考auto简介auto关键字的特性类型别名的思考 随着程序越来越复杂,程序中用到的类型也越来越复杂,经常体现在: 类型难于拼写含义不明确导致容易出错 #include <string> #include <map> int main() {std::ma…...

nodejs的后端框架egg,thinkjs,nestjs,nuxtjs,nextjs对比
1. Egg.js:优点:Egg.js是一个基于Koa的Node.js企业级应用开发框架,它提供了完整的开发规范和一套稳定性和安全性较高的架构体系,能够帮助开发者快速构建高可用、高性能的应用程序。同时,Egg.js还提供了很多自定义插件和…...

SpringBoot @SpringBootTest 无法启动服务
这几天在看Hikari、Druid连接池。按照网上代码写Junit测试类。当时代码如下: package com.ceaning.crudp.utils;import org.junit.Test; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.boot.test.context.SpringBootTest; impo…...
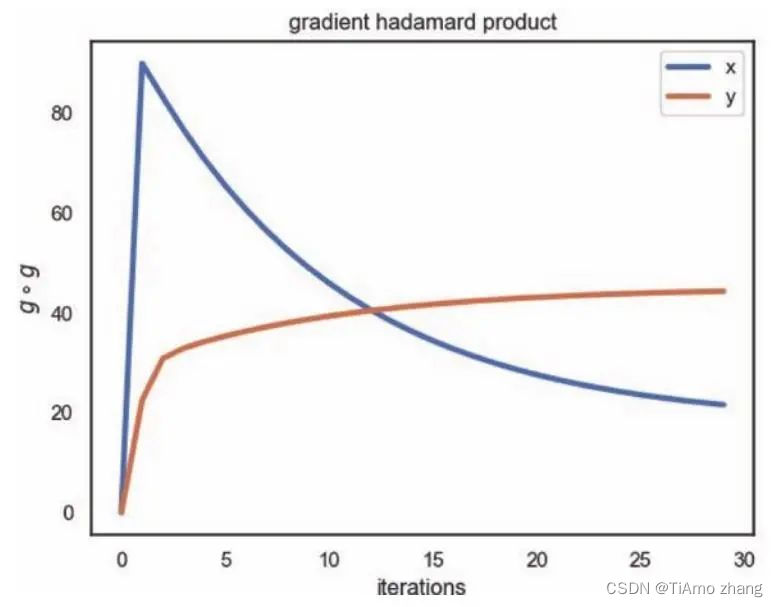
PyTorch深度学习实战 | 神经网络的优化难题
即使我们可以利用反向传播来进行优化,但是训练过程中仍然会出现一系列的问题,比如鞍点、病态条件、梯度消失和梯度爆炸,对此我们首先提出了小批量随机梯度下降,并且基于批量随机梯度下降的不稳定的特点,继续对其做出方…...
如何缩小pdf文件的大小便于上传?在线压缩pdf工具推荐
平时在工作、学习时我们经常都需要用到pdf文件,那么当遇上需要将pdf压缩大小的时候,该使用哪种pdf压缩(https://www.yasuotu.com/pdfyasuo)方式呢?今天分享一个在线压缩pdf的方法,需要的小伙伴一起来了解…...
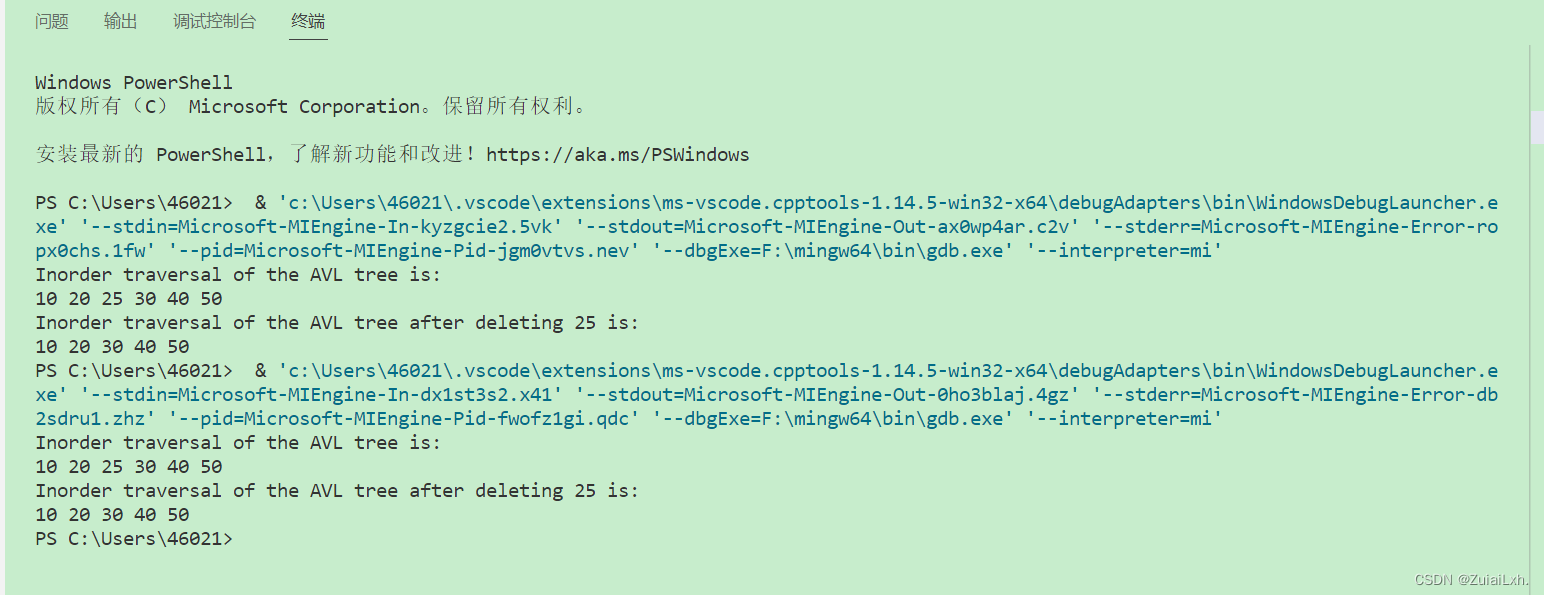
使用C++编写一个AVL的增删改查代码并附上代码解释
//qq460219753提供其他代码帮助 #include <iostream> using namespace std;struct Node {int data;Node *left;Node *right;int height; };// 获取结点高度 int height(Node *node) {if (node nullptr){return 0;}return node->height; }// 获取两个数中较大的一个 i…...

React/ReactNative 状态管理: redux-toolkit 如何使用
有同学反馈开发 ReactNative 应用时状态管理不是很明白,接下来几篇文章我们来对比下 React 及 ReactNative 状态管理常用的几种框架的使用和优缺点。 上一篇文章介绍了 redux 的使用,这篇文章我们来看下 redux 的升级版:redux-toolkit。 下…...

14基于双层优化的电动汽车优化调度研究
说明书 MATLAB代码:基于双层优化的电动汽车优化调度研究 关键词:双层优化 选址定容 输配协同 时空优化 参考文档:《考虑大规模电动汽车接入电网的双层优化调度策略_胡文平》中文版 《A bi-layer optimization based temporal and sp…...

古茗科技面试:为什么 ElasticSearch 更适合复杂条件搜索?
文章目录 ElasticSearch 简介倒排索引联合索引查询跳表合并策略Bitset 合并策略MySQL 最多使用一个条件涉及的索引来过滤,然后剩余的条件只能在遍历行过程中进行内存过滤。 上述这种处理复杂条件查询的方式因为只能通过一个索引进行过滤,所以需要进行大量的 I/O 操作来读取行…...
【数据结构】哈希表
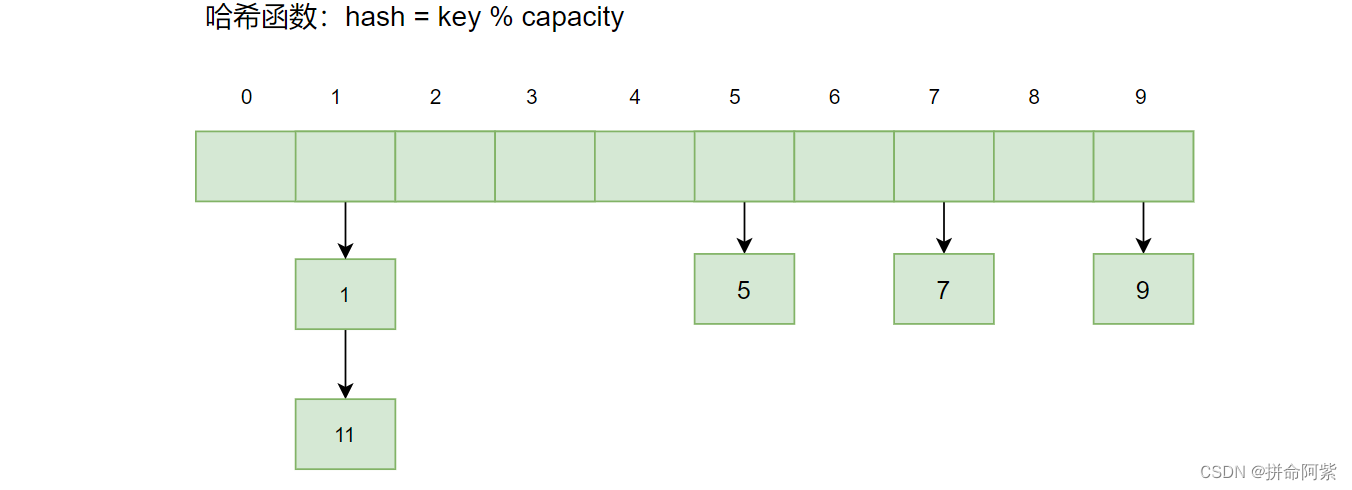
目录 1、哈希表 1.1 哈希表的简介 1.2 降低哈希冲突率 1.3 解决哈希冲突 1.3.1 闭散列 1.3.2 开散列(哈希桶) 1、哈希表 1.1 哈希表的简介 假设我们目前有一组数据,我们要从这组数据中找到指定的 key 值,那么咱们目…...

物联网常用协议MQTT协议相关介绍
概述 MQTT(Message Queuing Telemetry Transport)是一种轻量级的消息传输协议,旨在在网络带宽有限的情况下,为物联网设备之间的通信提供可靠的、低延迟的消息传递服务。MQTT协议具有订阅/发布模式,支持多种传输协议&a…...

【C语言进阶】13. 假期测评②
day10 1. int类型字节数 求函数返回值,传入 -1 ,则在64位机器上函数返回( ) int count 0; int x -1; while (x) {count;x x >> 1; } printf("%d", count);A: 1 B: 2 C: 32 D: 死循环,没结果 【答案解析】C xx&(x-1)这…...

【国产FPGA】国产FPGA搭建图像处理平台
最近收到了高云寄过来的FPGA板卡,下图:来源:https://wiki.sipeed.com/hardware/zh/tang/tang-primer-20k/primer-20k.htmlFPGA主要参数:FPGA型号参数GW2A-LV18PG256C8/I7逻辑单元(LUT4) 20736寄存器(FF) 15552分布式静态随机存储器S-SRAM(bit…...
你的应用太慢了,给我司带来了巨额损失,该怎么办
记得很久之前看过谷歌官方有这么样的声明:如果一个页面的加载时间从 1 秒增加到3 秒,那么用户跳出的概率将增加 32%。 但是早在 2012 年,亚马逊就计算出了,页面加载速度一旦下降一秒钟,每年就会损失 16 亿美元的销售额…...

第十四届蓝桥杯三月真题刷题训练——第 22 天
目录 第 1 题:受伤的皇后_dfs 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 思路: 第 2 题:完全平方数 问题描述 输入格式 输出格式 样例输入 1 样例输出 1 样例输入 2 样例输出 2 评测用例规模与约…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
