算法全面剖析
算法
查找算法:
顺序查找:
基本思想:
顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败(-1)
时间复杂度:
查找成功时的平均查找长度为:(假设每个数据元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;当查找不成功时,需要n+1次比较,时间复杂度为O(n);
所以,顺序查找的时间复杂度为O(n)。
基本程序:
int SequenceSearch(int a[], int value, int n){
for(int i=0; i<n; i++){if(a[i] == value){return i;}
}
return -1;
}
二分查找:
前提条件:
元素必须是有序的,如果是无序的则要先进行排序操作
基本思想:
二分查找也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点
时间复杂度:
最坏情况下,关键词比较次数为log2(n+1),且期望时间复杂度为O(log2n);
基本程序:
int BinarySearch1(int a[], int value, int n){int low, high, mid;low = 0;high = n-1;while(low<=high){mid = (low+high)/2;if(a[mid]==value){return mid;}else if(a[mid]>value){high = mid-1;}else if(a[mid]<value){low = mid+1;}}return -1;
}
注:折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议用 ——《大话数据结构》
排序算法:
比较排序:
冒泡排序:
简介:
冒泡排序(英语:Bubble Sort)又称为泡式排序,是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端
时间/空间复杂度:
时间复杂度最坏情况下为O(n2),最坏情况下为O(n),平均下来约为O(n2)
空间复杂度为O(1);
稳定性:
因排序后相同数字的顺序不变,所以为稳定
代码:
基础法:
void bubblesort(int a[],int n){for (int i = n - 1; i > 0; i--) {for (int j = 0; j < i; j++) {if (a[j] > a[j + 1])swap (a[j], a[j + 1]);}}
}
提速法:
void bubble_sort(int a[],int n){bool flag=true;while (flag){flag=false;for (int i=1;i<n;i++){//检查一遍if (a[i]>a[i-1]){//如果当前数大于前一个falg=true;swap(a[i],a[i-1]);//调换位置}else {//如果不是,就将falg设为false,然后就会跳出循环falg=false;}}}
}
选择排序:
简介:
选择排序( Selection sort)是一种简单直观的排序算法。一般是初学者接触的第一个排序算法,简称为选排。它的工作原理是每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完
时间/空间复杂度:
时间复杂度在最好的情况下为O(n2),在最坏得到情况下也是O(n2),所以平均时间复杂度也是O(n^2)
空间复杂度为O(1)
稳定性:
因为排序完成后,两个相同数字的数的顺序变了,所以为不稳定
代码:
void selection_sort(int a[],int n){int k;for (int i=0;i<n;i++){k=i;for (int j=i;j<n;j++){if (a[j]<a[k]){//在未排序区域找最小值k=j;//并将k设为当前的编号}}swap(a[i],a[k]);}
}
插入排序:
简介:
直接插入排序是将无序序列中的数据插入到有序的序列中,在遍历无序序列时,首先拿无序序列中的首元素去与有序序列中的每一个元素比较并插入到合适的位置,一直到无序序列中的所有元素插完为止,即每一步将一个待排序的数据插入到前面已经排好序的有序序列中,直到插完所有元素为止
时间/空间复杂度:
在最好的情况下,时间复杂度为O(n),最坏情况下为O(n2),所以平均时间复杂度为O(n2)
空间复杂度为O(1)
稳定性:
因为排序后相同的数字的位置不变,所以为稳定
代码:
void insertsort(int a[],int n){for (int i=1;i<n;i++){int key=a[i];int j=i-1;while (j>=0&&a[j]>key){//寻找位置,并挪移a[j+1]=a[j];j--;}a[j+1]=key;//储存}
}
非比较排序:
计数排序:
简介:
对于每一个输入元素 x,确定小于 x 的元素个数,利用这一信息,就可以直接把 x 放到它在输出数组中的位置上了。例如,如果有 17 个元素小于 x, 则 x就应该在第 18 个输出位置上。当有几个元素相同时,这一方案要略做修改,因为不能把他们放在同一个输出位置上
时间/空间复杂度:
时间复杂度在最好情况和最坏情况下都为O(n+k),所以平均时间复杂度也为O(n+k)
空间复杂度为o(k)
稳定性:
因为排序完成后相同数字的位置不变,所以为稳定
代码:
void counting_sort(int a[],n){int b[100000],cnt[100000];//b为顺序for (int i = 0; i < n; i++) {b[a[i]]++;//存储每一个数比他小的数的个数}for (int i=1;i<=n;i++){b[i]+=b[i-1];}//计算前缀和for (int i=n-1;i>=0;i--){cnt[b[a[i]]--]=a[i];//放入对应的位置}
}
贪心算法:
本质:
利用贪心算法对问题求解时,考虑的并不是对于整体最好的策略,而是总是做出当前看来最好的选择,即贪心算法所作出的选择仅仅是在某种情况下的局部最优解
思路:
1.建立数学模型来解决问题
2.把求解的问题分解成多个子问题(类似于递归)
3.对每个子问题进行求解局部最优解
4.将数据归纳,合并成原来问题的一个解
实现框架:
while/* 或 for */(/*所写内容:向给定的总目标前进一步*/){//利用可行的策略,求解出一个可行的元素,并保存}
//由所有可行的元素合成一个可行的解
注意事项:
贪心算法并不能一定得到最优解,它只是局部的最优解,所以使用贪心算法有一个大前提,就是局部的最优策略可以产生全局的最优解,除此之外,任何情况都不能完全的使用贪心算法,但有些时候可以利用贪心算法的部分思想
例题分析:
简单贪心算法:
小明去购物,想要买的食品如下,当前小明能拎回的重量不超过15斤,那么小明能拎回的食品的数量最多为?
| 食物 | 牛奶 | 面包 | 方便面 | 苹果 | 饼干 | 榴莲 | 西瓜 |
|---|---|---|---|---|---|---|---|
| 重量/斤 | 4.5 | 1 | 2 | 3.3 | 2.8 | 6.2 | 8.4 |
分析思路:
想要得到最多的食品,那么利用贪心算法的策略就应该是每次都选择当前最轻的,这样最后拿到的总数才最多
实现过程:
首先对当前食品按照重量从小到大的顺序进行排序,排序结果如下
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 食物 | 面包 | 方便面 | 饼干 | 苹果 | 牛奶 | 榴莲 | 西瓜 |
| 重量/斤 | 1 | 2 | 2.8 | 3.3 | 4.5 | 6.2 | 8.4 |
然后按照贪心策略进行选择,过程如下
i=0,放入后当前重量为1,不超过15,可以,现在的总数量加1
i=1,放入后当前重量为3,不超过15,可以,现在的总数量加1
i=2,放入后当前重量为5.8,不超过15,可以,现在的总数量加1
i=3,放入后当前重量为9.1,不超过15,可以,现在的总数量加1
i=4,放入后当前重量为13.6,不超过15,可以,现在的总数量加1
i=5,放入后当前重量为19.8,超过15,不可以,现在的总数量不变
i=6,放入后当前重量为22,超过15,不可以,现在的总数量不变
综上可以得知,最多可以带回去的数量为5
样例代码:
double w;//能拎动的的食品的总重量
int n,sum=0,tmp=0;//n为想买的总数量,sum为能拎回去的总数量,tmp为当前准备拎回去的食品的重量
double wg[10];//想买的每件食品的重量
sort(wg,wg+n);//按照从小到大的顺序进行排序
for (int i=0;i<n;i++){//贪心算法tmp+=wg[i];if (tmp<=tw){//如果当前重量小于或等于能拎动的总数量sum++;//就将能拎回去的总数量加1}else{break;//否则就跳出循环}
}
复杂贪心算法:
如果这时小明想要让拎回去的价值最高,那么这个价格又是多少呢?(其他条件与上题一样)
| 食物 | 牛奶 | 面包 | 方便面 | 苹果 | 饼干 | 榴莲 | 西瓜 |
|---|---|---|---|---|---|---|---|
| 价格/元 | 18 | 3 | 7.8 | 15.8 | 8 | 99.2 | 20.2 |
| 重量/斤 | 4.5 | 1 | 2 | 3.3 | 2.8 | 6.2 | 8.4 |
分析思路:
根据贪心算法,现在每一次所选择的食品的价格必须是最高的,但是价格高的食物也有可能很重,所以这时我们就要考虑一个新的东西——性价比(或单价),即价格/重量,那么由此就可以按照性价比从大到小进行排序,然后按照贪心算法进行选择每一次性价比最高的食品,并进行比较,看看重量增加后是否还能拎回去
实验过程:
首先按照性价比由大到小进行排序,结果如下
| 食物 | 榴莲 | 苹果 | 牛奶 | 方便面 | 饼干 | 面包 | 西瓜 |
|---|---|---|---|---|---|---|---|
| 价格/元 | 99.2 | 15.8 | 18 | 7.8 | 8 | 3 | 20.2 |
| 重量/斤 | 6.2 | 3.3 | 4.5 | 2 | 2.5 | 1 | 8.4 |
| 性价比 | 16 | 4.8 | 4 | 3.9 | 3.2 | 3 | 2.4 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
然后按照贪心策略进行选择,过程如下
i=0,放入后重量为6.2,不超过15,可以,此时总价值为99.2
i=1,放入后重量为9.5,不超过15,可以,此时总价值为115
i=2,放入后重量为14,不超过15,可以,此时总价值为133
i=3,放入后重量为16,超过15,不可以,此时总价值为133
i=4,放入后重量为16.5,超过15,不可以,此时总价值为133
i=5,放入后重量为15,不超过15,可以,此时总价值为136
i=6,放入后重量为23.4,超过15,不可以,此时总价值为136
综上可知,小明能够带回去的食品的最大价值为136元
样例代码:
struct food{double w,p,j;//w为重量,p为价格,j为性价比
}wg[10];
double k,tmp;//k能拎动的的食品的总重量,tmp为当前准备拎回去的食品的重量
int n,sum;//n为想买的总数量,sum为能拎回去的总资产
sort (wg,wg+n,cmp);//按照性价比从大到小进行排序
for (int i=0;i<n;i++){//贪心算法tmp+=w[i].w;if (tmp<=k){//如果可以拎动sum+=w[i].p;//就将总资产加上当前这个食品的价格}else {tmp-=w[i].w;//否则就从准备拎回去的食品的重量里删除当前食品的重量}
}
洛谷例题:【深基12.例1】部分背包问题
题目描述
阿里巴巴走进了装满宝藏的藏宝洞。藏宝洞里面有 N(N<= 100)堆金币,第 i 堆金币的总重量和总价值分别是 mi,vi(1<=mi,vi<= 100)。阿里巴巴有一个承重量为 T(T <= 1000)的背包,但并不一定有办法将全部的金币都装进去。他想装走尽可能多价值的金币。所有金币都可以随意分割,分割完的金币重量价值比(也就是单位价格)不变。请问阿里巴巴最多可以拿走多少价值的金币?
输入格式
第一行两个整数 N,T。
接下来 N行,每行两个整数 mi,vi。
输出格式
一个实数表示答案,输出两位小数
样例输入 #1
4 50
10 60
20 100
30 120
15 45
样例输出 #1
240.00
分析思路:
因为金币可以分割,所以可以用性价比来排序(从大到小),从而获得结果
样例代码:
#include <bits/stdc++.h>
using namespace std;double value;
struct gold{double m,v,o;
}a[120];bool cmp(gold a1,gold a2){return a1.o>a2.o;
}int main() {int n,t;cin>>n>>t;for (int i=0;i<n;i++){cin>>a[i].m>>a[i].v;a[i].o=a[i].v/a[i].m;}sort(a,a+n,cmp);for (int i=0;i<n;i++){if (a[i].m<=t){t-=a[i].m;value+=a[i].v;}else if (t>0&&t<a[i].m){value+=t*a[i].o;break;}}printf("%.2lf",value);return 0;
}分治算法:
本质:
分治算法如同字面上说的一样,就是把一个大问题分解成多个小问题,再把每个小问题再分解成更小的问题,直到每一个问题都能够简单的求解为止,向上归纳,就可以得出原问题的答案为所有小问题的解的合并
思路:
(1)建立二叉树模型
(2)将求解的问题分解成多个子问题,然后继续分解,直到能简单求解为止
(3)从最后一层开始向上递推,直到求出原问题的解
实现框架:
int que(int q){//建立函数if (){//如果条件成立,即可以简单求解return ;//就返回求解答案}return ;//如果不可以就继续分解
}
注意事项:
如果遇到数据集较小的题目,建议不要使用分治算法,这样不仅浪费时间,还会浪费空间,很容易错失良机
例题分析:
已知有n个数(10000>=a[i])放在数组a中,请用分治算法求解这n个数中的最大值
分析思路:
想要解决这个问题,第一步就是要“分”,顾名思义就是按照二分法将原问题分解成简单的子问题,第二步就是“治”了,即从最下一层开始,向上反推,逐步和解,最终得出答案
实现过程:
分:
将{43556,23452,33259,24955,112142,234074,36467}
分成{43556,23452,33259,24955}与{112142,234074,36467}
继续分为{43556,23452}与{33259,24955}与{112142,234074}与{36467}
现在已经可以比较了,所以进行“治”
治:
{43556,23452}中得出大者为43556,{33259,24955}中得出大者为33259,{112142,234074}中得出大者为234074,{36467}中得出大者为36467
归纳上去,可得到{43556,33259}与{234074,36467}
继续比较可从{43556,33259}中得出大者为43556,{234074,36467}中得出大者为234074
再次归纳可得到{43556,234074}
再次比较可从{43556,234074}得出最大者为234074
至此算法结束,可得到最大者为234074
样例代码:
int max(inr a[],int i,int j){//i为左边界,j为右边界int num1=0;num2=0;//为下处比较使用if (i==j)return a[i];//如果左右边界相等,即此时只有一个数据,就直接返回这个数据else if (i==j-1){//如果左边界等于右边界-1,即此时有两个数据,就返回大的那个数据if (a[i]>=a[j)return a[i];else return a[j];}else {//如果不是,就按照二分法再次进行分段int mid=(i+j)/2;//取中点//利用递归进行寻找num1=max(a,i,mid);num2=max(a,mid,j);if (num1>=num2)return num1;//比较大小,返回大值else return num2;}
}
回溯算法:
本质:
即在搜索的尝试过程中,当发已经满足不了求解条件是,利用**“回溯”返回**到上一步,重新选择路线
思路:
(1)正常进行寻找和判断
(2)将一条路探索完
(3)返回到上一次选择方向的地点
实现框架:
模式一:
int search(int k){for (int i=0;i<n/*n为算法总数*/;i++){if(/*满足条件*/){//保存结果}if(/*到达目标*/){//输出结果}else {search(k+1);}//恢复到保存结果之前的状态,即回溯一步}
}
模式二:
int search(int k){if (/*到达目标*/){//输出结果}else {for (int i=0;i<n/*n为算法总数*/;i++){if ((/*满足条件*/){//保存结果search(k+1);//恢复到保存结果之前的状态,即回溯一步}}}
}
注意事项:
回溯算法利用的是深度优先搜索的思想,这种算法会很容易超时,容易崩端,所以在使用的时候一定要留足时间
例题分析:
已知一个迷宫以及迷宫的入口和出口,现从迷宫的入口进入,看看是否存在一条路通往出口,如果存在,输出“YES”,如果不存在,就输出“NO”
迷宫造型如下(灰色代表墙壁)

分析思路:
我们利用“搜索与回溯”的方法进行寻找,即从入口开始,顺着某一方向进行探索,如果能走通,就继续往下走,如果不行就原路返回,换一个方向继续探索,直到所有的路都探索完位置,如果全部都探索完了仍然没有路可以通往出口,就说明没有通往出口的道路
实验过程:

上图解释:
从入口开始探索,先向右探索,探索两个后碰壁(a),调整方向(b)、(c)、(d),最后发现无路可走,回溯到上一步。
方向调为向下,到下一格,向右探索(e),碰壁,向下探索一步,在此基础上向右探索,成功,继续直到碰壁(g),调整方向,向下,到达出口,成功,探索结束,输出YES
样例代码:
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
//初始化前,下,后,上
int x,y,x1,y1,nx,ny,n;
bool visited[100][100],flag=false;
int dfs(int x,int y){if (x==x1&&y==y1){//到达cout<<"YES"<<endl;flag=true;return 1;}for (int i=0;i<4;i++){//搜索四个方向nx=x+dx[i];ny=y+dy[i];if (nx<0||nx>=n||ny<0||ny>n){//判断是否越界continue;}if (visited[nx][ny]==false){visited[nx][ny]=true;//标记为走过dfe(nx,ny);//然后在此基础上继续往下探索visited[nx][ny]=false;//回溯,即标记为未走过}}return 0;
}
相关文章:

算法全面剖析
算法 查找算法: 顺序查找: 基本思想: 顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功&am…...

tp5php7.4配置sqlserver问题汇总
先修改database.php文件 查看php版本选择sqlserver扩展 通过百度网盘分享的文件:sqlserver 链接:https://pan.baidu.com/s/1zrIV8VWQZM9miLpyH01Aww?pwdxdgx 提取码:xdgx 通过我的分享链接复制自己需要的dll到php的ext下 在php.ini里添加扩…...

C语言随笔:字面量
字面量(Literal)是指程序源代码中直接写出的固定值。字面量用于表示数据常量,它们在程序编译时被直接解析并用于程序运行。 常见的字面量类型 整数字面量(Integer Literals) 描述:表示整数值。示例&#x…...

chainlit的基本概念聊天对话中的元素
文本消息是聊天机器人的组成部分,但我们通常希望向用户发送的不仅仅是文本,还包括图像、视频等。 这就是元素出现的地方。每个元素都是一段内容,可以附加到Message或Step 并显示在用户界面上。 chainlit支持的元素如下: 文本元…...
)
【LeetCode:3】无重复字符串的最长子串(Java)
题目链接 3. 无重复字符串的最长子串 题目描述 给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。 示例 2: 输入: s “bbb…...

C#对字典使用Linq查询
Dictionary<int, int> dic new Dictionary<int, int>();dic.Add(1, 2);dic.Add(2, 3);dic.Add(3, 4);dic.Add(4, 5);dic.Add(5, 6);//筛选键var keys dic.Where(item > item.Key > 2).Select(item > item.Key);foreach (var item in keys){Console.Writ…...

【Vue】Vue基础
系列文章目录 第二章 Vue基础(1) 文章目录 系列文章目录第一节:Vue介绍一、Vue介绍二、Vue项目创建三、项目结构介绍 第二节:组合式API一、基本介绍二、setup介绍三、setup上指定组件名称 第三节:响应式变量一、使用r…...

贪心 + 分层图bfs,newcoder 76652/B
目录 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 二、解题报告 1、思路分析 2、复杂度 3、代码详解 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 https://ac.nowcoder.com/acm/contest/76652/B 二、解题报告 1、思路分析…...

如何在Linux上部署Java Web应用程序
在Linux上部署Java Web应用程序是一个常见的任务,本文将介绍一种常用的方法,分为以下几个步骤: 准备服务器 首先,你需要准备一台运行Linux操作系统的服务器。你可以选择使用各种不同的Linux发行版,如Ubuntu、CentOS等…...
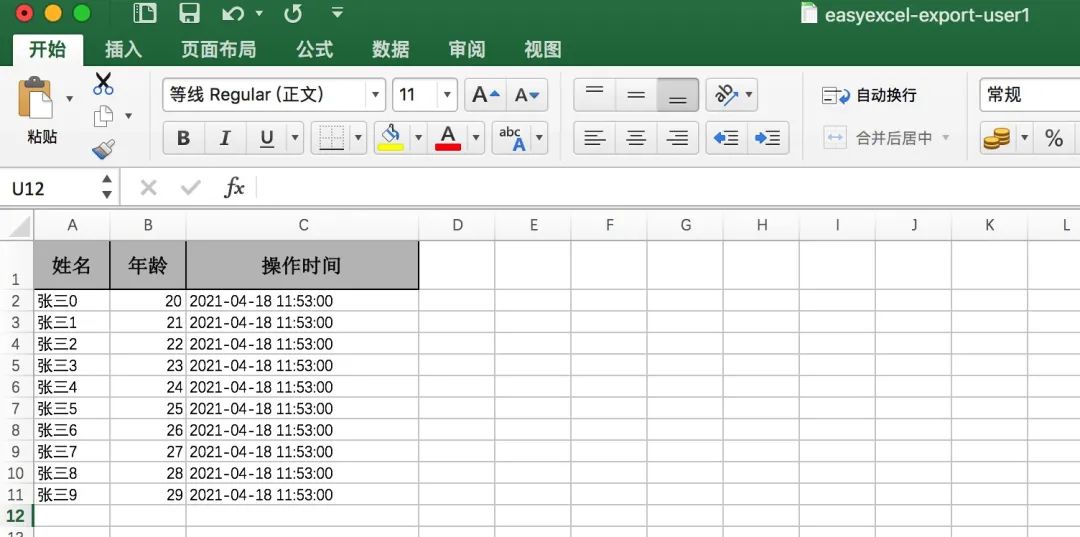
SpringBoot 整合 Excel 轻松实现数据自由导入导出
01、背景介绍 在实际的业务系统开发过程中,操作 Excel 实现数据的导入导出基本上是个非常常见的需求。 之前,我们有介绍一款非常好用的工具:EasyPoi,有读者提出在数据量大的情况下,EasyPoi 会占用内存大,…...
- 混合精度训练)
PyTorch 基础学习(13)- 混合精度训练
系列文章: 《PyTorch 基础学习》文章索引 基本概念 混合精度训练是深度学习中一种优化技术,旨在通过结合高精度(torch.float32)和低精度(如 torch.float16 或 torch.bfloat16)数据类型的优势,…...

Mycat分片-垂直拆分
目录 场景 配置 测试 全局表配置 续接上篇:MySQ分库分表与MyCat安装配置-CSDN博客 续接下篇:Mycat分片-水平拆分-CSDN博客 场景 在业务系统中, 涉及以下表结构 ,但是由于用户与订单每天都会产生大量的数据, 单台服务器的数据 存储及处理能力是有限…...

一元四次方程求解-【附MATLAB代码】
目录 前言 求解方法 编辑 MATLAB验证 附:一元四次方程的故事 前言 最近在研究机器人的干涉(碰撞)检测,遇到了一个问题,就是在求椭圆到原点的最短距离时,构建的方程是一个一元四次方程。无论是高中的…...

【极限性能,尽在掌控】ROG NUC:游戏与创作的微型巨擘
初见ROG NUC,你或许会为它的小巧体型惊讶。然而,这看似不起眼的机身内,蕴藏着游戏、创意的强大能量。 掌中风暴,性能无界 ROG NUC搭载英特尔高性能处理器,配合高速NVMe SSD固态硬盘以及可选的高端独立显卡(…...

Ecosmos开启公测,将深度赋能CIOE中国光博会元宇宙参会新体验
如今,生成式AI技术的发展,极大地降低了3D数字资产的制作成本,元宇宙作为一种可以无缝将物理和数字资产进行融合的技术,在推动电子产业数字化进程、助力产业高质量发展的方面展现出了巨大的潜力。 当前,发展新质生产力是…...
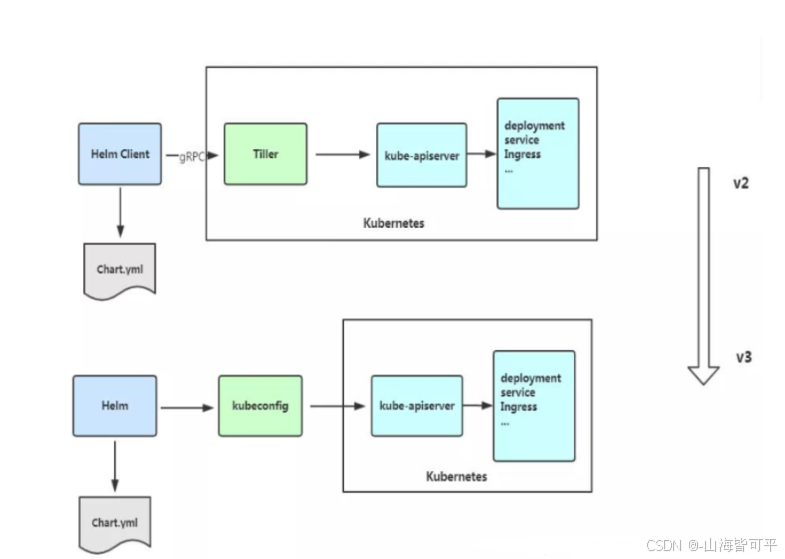
【Kubernetes】k8s集群之包管理器Helm
目录 一.Helm概述 1.Helm的简介 2.Helm的三个重要概念 3.Helm2与Helm3的的区别 二.Helm 部署 1.安装 helm 2.使用 helm 安装 Chart 3.Helm 自定义模板 4.Helm 仓库 每个成功的软件平台都有一个优秀的打包系统,比如Debian、Ubuntu 的 apt,RedH…...
)
嵌入式linux系统镜像制作day3(构建镜像)
点击上方"蓝字"关注我们 01、上节回顾 嵌入式linux系统镜像制作day1嵌入式linux系统镜像制作day2提前下载好准备工具,不然失败了大眼瞪小眼。 02、构建 Poky 的 Sato 镜像1 环境: ubuntu18.04poky版本:Dizzy 工具git 在开始之前,针对不同的发行版,需要先执行…...

【生日视频制作】教师节中秋节国庆节车模特美女举牌AE模板修改文字软件生成器教程特效素材【AE模板】
教师节中秋节国庆节车模特美女举牌生日视频制作教程AE模板改文字软件生成器素材 怎么如何做的【生日视频制作】教师节中秋节国庆节车模特美女举牌AE模板修改文字软件生成器教程特效素材【AE模板】 生日视频制作步骤: 安装AE软件下载AE模板把AE模板导入AE软件修改图…...
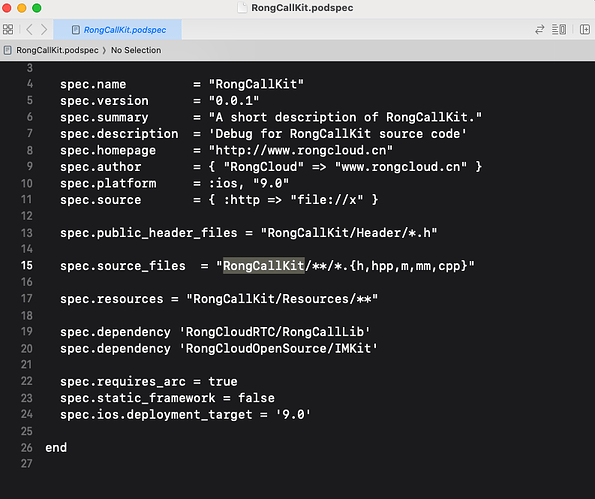
RongCallKit iOS 端本地私有 pod 方案
RongCallKit iOS 端本地私有 pod 方案 需求背景 适用于源码集成 CallKit 时,使用 pod 管理 RTC framework 以及源码。集成 CallKit 时,需要定制化修改 CallKit 的样式以及部分 UI 功能。适用于 CallKit 源码 Debug 调试便于定位相关问题。 解决方案 从…...

C++11:可变参数模板
目录 一、概述 二、场景 1.深拷贝的类 2.浅拷贝的类 C使用指南 一、概述 // Args是一个模板参数包,args是一个函数形参参数包 // 声明一个参数包Args...args,这个参数包中可以包含0到任意个模板参数。 template <class ...Args> void ShowList(…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
