【机器学习】逻辑回归原理(极大似然估计,逻辑函数Sigmod函数模型详解!!!)

目录
🍔 逻辑回归应用场景
🍔 极大似然估计
2.1 为什么要有极大似然估计?
2.2 极大似然估计步骤
2.3 极大似然估计的例子
🍔 Sigmod函数模型
3.1 逻辑斯特函数的由来
3.2 Sigmod函数绘图
3.3 进一步探究-加入线性回归
3.4 结果解释
3.5 对数似然损失函数
🍔 逻辑回归应用场景
在KNN算法中直接可以得出预测结果,但是如果想输出预测结果,还要输出预测结果的概率,这时候就需要使用逻辑回归解决问题。
比如,预测性别的时候,预测为男性,同时预测概率为90%,这样可以通过概率更加具有说服力。
🍭 应用场景
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归。由于算法的简单和高效,在实际中应用非常广泛。
广告点击率
是否为垃圾邮件
是否患病
金融诈骗
虚假账号
看到上面的例子,我们可以发现其中的特点,那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器。
🍔 极大似然估计
2.1 为什么要有极大似然估计?
例子:我与一位猎人一起外出打猎,一只野兔从前方穿过,只听到一声枪响,野兔应声倒下。问是谁倒下的呢?
答:极有可能是猎人。
显然候选人就两个,我和猎人。若选择我,则事件发生的发生概率为0.01%,因为我不会打猎;若选择猎人,则事件发生的概率为99%,而事件已经发生,因此选择猎人更为合适。
🐼 极大似然估计的思想:
设总体中含有待估参数w,可以取很多值。已经知道了样本观测值(例子中的兔子被猎人打死了),从w的一切可能值中(引例中是我和猎人)选出一个使该观察值出现的概率为最大的值,作为w参数的估计值,这就是极大似然估计。(顾名思义:就是看上去那个是最大可能的意思)
2.2 极大似然估计步骤
🐻 求极大似然函数估计值的一般步骤:
(1) 写出似然函数;
(2) 对似然函数取对数,并整理;
(3) 求导数 ;
(4) 解似然方程
极大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。极大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
当然极大似然估计只是一种粗略的数学期望,要知道它的误差大小还要做区间估计。
🍔 Sigmod函数模型
3.1 逻辑斯特函数的由来
🐼 Sigmod函数,也称之为逻辑斯特函数
假设一事件发生的概率为P,则不发生的概率为1-P,我们把发生概率/不发生概率称之为发生的概率比,数学公式表示为:
更进一步我们定义logit函数,它是概率比的对数函数(log-odds)
Logit函数耳朵输入值范围介于[0,1]之间,它能将输入转换到整个实数范围内。
对logit函数求反函数,我们将logit的反函数叫做logistic函数:
该函数的图像如下图:
对图像的理解:sidmod函数以实数值作为输入并将其反射到[0,1]区间,拐点在y=0.5地方。
3.2 Sigmod函数绘图
🍭 需求:绘制[-7,7]的sigmod函数图像
import matplotlib.pyplot as plt
import numpy as npdef sigmod(z):return 1.0/(1.0+np.exp(-z))z=np.arange(-7,7,0.1)
phi_z=sigmod(z)plt.plot(z,phi_z)
plt.axvline(0.0,color='k')
plt.axhspan(0.0,1.0,facecolor='1.0',alpha=1.0,ls='dotted')
plt.yticks([0.0,0.5,1.0])
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.show()函数图像如图所示💯 :
逻辑回归的分类结果是通过属于某个类别的概率值来判断
预测概率大于 50% 则分为类1类别(正例), 反之为0类别(反例)
3.4 结果解释
输出结果解释(重要):假设有两个类别A,B,并且假设我们的概率值为属于A(1)这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果0.55,那么这个概率值超过0.5,意味着我们训练或者预测的结果就是A(1)类别。那么反之,如果得出结果为0.3那么,训练或者预测结果就为B(0)类别。
关于逻辑回归的阈值是可以进行改变的,比如上面举例中,如果你把阈值设置为0.6,那么输出的结果0.55,就属于B类。
在学习逻辑回归之前,我们用均方误差来衡量线性回归的损失。
🐼 在逻辑回归中,当预测结果不对的时候,我们该怎么衡量其损失呢?
我们来看下图(下图中,设置阈值为0.6),

那么如何去衡量逻辑回归的预测结果与真实结果的差异?
首先我们进行逻辑斯特回归函数的表示学习。
3.5 对数似然损失函数
假设:有 0、1 两个类别,某个样本被分为 1 类的概率为: p, 则分为 0 类的概率为 1-p,则每一个样本分类正确的概率为:
上述公式可转换为:
假设,我们现在有样本:[(x1, y1), (x2, y2) … (xn, yn)],那么,全部预测正确的概率表示为:
通过极大化事件概率,从而估计出模型参数。
接下来,将上式其转换为对数加法的形式:
上述公式为最大化问题。
增加一个负号,将其变为最小化问题,公式再次转换如下:
此时,得到逻辑回归的对数似然损失函数.
如上述案例,我们就带入上面那个例子来计算一遍,就能理解意义了。

我们已经知道,-log(P), P值越大,结果越小,所以我们可以对着这个损失的式子去分析。
相关文章:

【机器学习】逻辑回归原理(极大似然估计,逻辑函数Sigmod函数模型详解!!!)
目录 🍔 逻辑回归应用场景 🍔 极大似然估计 2.1 为什么要有极大似然估计? 2.2 极大似然估计步骤 2.3 极大似然估计的例子 🍔 Sigmod函数模型 3.1 逻辑斯特函数的由来 3.2 Sigmod函数绘图 3.3 进一步探究-加入线性回归 3…...
网络热门编程项目导学:黑马点评
本文作者:程序员鱼皮 免费编程学习 - 编程导航网:https://www.code-nav.cn 大家好,我是鱼皮。 之前已经给大家分享了三个全栈项目,比如瑞吉外卖什么的,这几个项目都是侧重于带大家学习框架的运用、以及一些简单的业务…...

如何在本地和远程删除 Git 分支?
如何在本地和远程删除 Git 分支? 欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 欢迎来到我的主页,我是博主英杰,211科班出身,就职于医疗科技公司,热衷分享知识,武汉城市开发者社区主理人 擅长.n…...

08 STM32 DMA
DMA 协助CPU,完成数据转运工作。 两个程序: DMA数据转运,DMAAD多通道 DMA数据转运,将使用DMA,进行存储器到存储器的数据转运,也就是把一个数组里面的数据,复制到另一个数组里。 定义一个数组D…...
)
LLM之基于llama-index部署本地embedding与GLM-4模型并初步搭建RAG(其他大模型也可,附上ollma方式运行)
前言 日常没空,留着以后写 llama-index简介 官网:https://docs.llamaindex.ai/en/stable/ 简介也没空,以后再写 注:先说明,随着官方的变动,代码也可能变动,大家运行不起来,可以进…...

Python 异步爬虫:高效数据抓取的现代武器
标题:“Python 异步爬虫:高效数据抓取的现代武器” 在当今信息爆炸的时代,网络爬虫已成为数据采集的重要工具。然而,传统的同步爬虫在处理大规模数据时往往效率低下。本文将深入探讨如何使用 Python 实现异步爬虫,以提…...
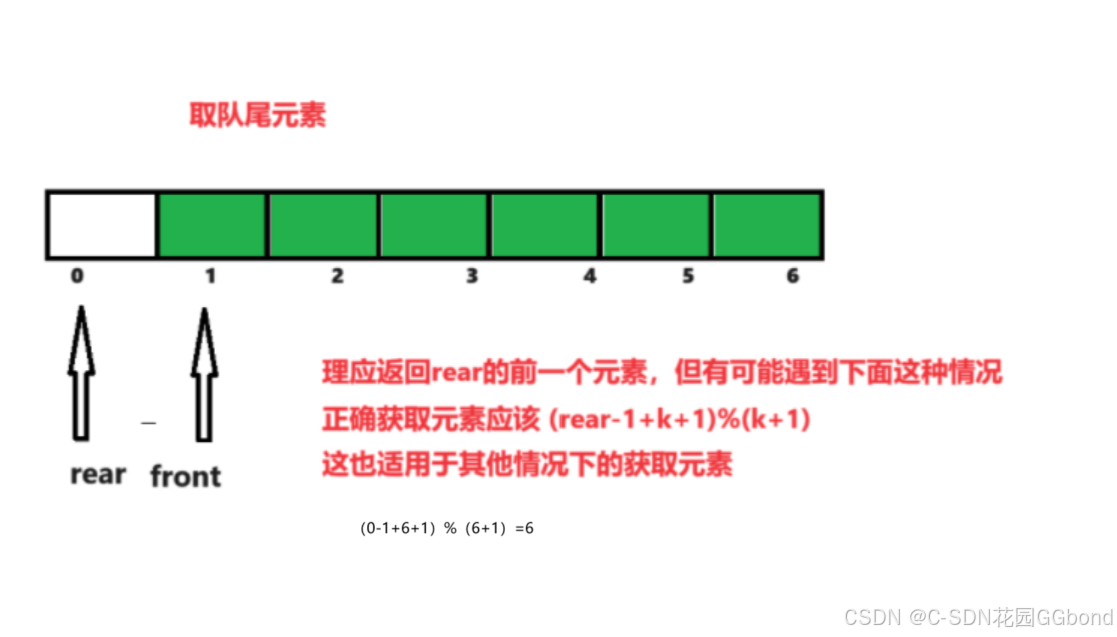
【数据结构算法经典题目刨析(c语言)】使用数组实现循环队列(图文详解)
💓 博客主页:C-SDN花园GGbond ⏩ 文章专栏:数据结构经典题目刨析(c语言) 目录 一.题目描述 二.解题思路 1.循环队列的结构定义 2.队列初始化 3.判空 4.判满 5.入队列 6.出队列 7.取队首元素 8.取队尾元素 三.完整代码实…...

PTA L1-005 考试座位号
L1-005 考试座位号(15分) 每个 PAT 考生在参加考试时都会被分配两个座位号,一个是试机座位,一个是考试座位。正常情况下,考生在入场时先得到试机座位号码,入座进入试机状态后,系统会显示该考生…...
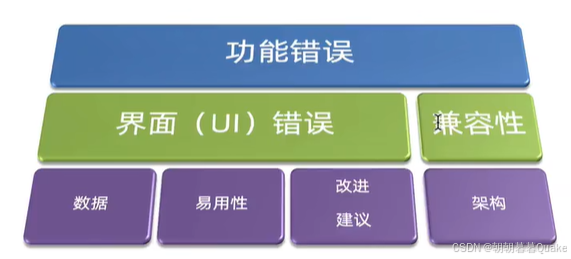
软件测试3333
禅道? 学习正则表达式 目标: 能说出软件测试缺陷判定标准 能说出项目中缺陷的管理系统 能使用Excel对于缺陷进行管理 能使用工具管理缺陷 一、用例执行 说明:用例执行不通过,执行结果与用例的期望结果不一致(含义&…...
))
JJJ:结构体定义中常加的后缀:attribute ((packed))
__attribute__ ((packed)): 的作用就是告诉编译器取消结构体在编译过程中的优化对齐,按照实际占用字节数进行对齐,是GCC特有的语法。这个功能是跟操作系统没关系,跟编译器有关 在GCC下:struct my{ char ch; int a;} sizeof(int)4…...

【HTML】DOCTYPE作用
<!DOCTYPE html> DOCTYPE是document type(文档类型)的缩写。是HTML5中一种标准通用标记语言的文档类型声明,告诉浏览器文档的类型,便于解析文档。不同渲染模式会影响浏览器对CSS代码甚至JS脚本的解析。它必须声明在第一行。…...
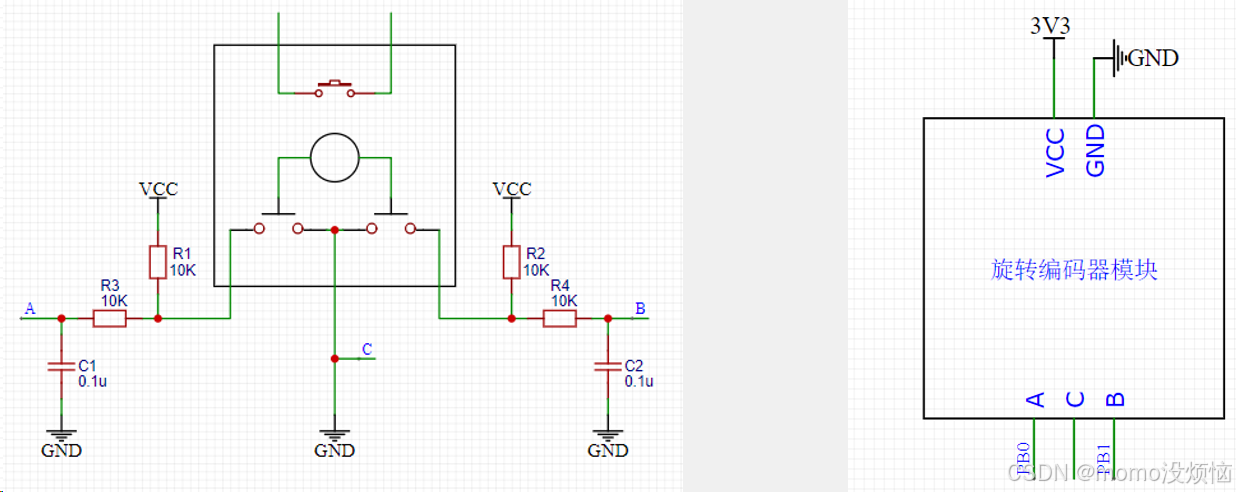
STM32学习记录-04-EXTI外部中断
1 中断系统 (1)中断:在主程序运行过程中,出现了特定的中断触发条件(中断源),使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继续…...
Android Studio 动态表格显示效果
最终效果 一、先定义明细的样式 table_row.xml <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_h…...

Python 全栈系列264 使用kafka进行并发处理
说明 暂时考虑的场景是单条数据处理特别复杂和耗时的场景。 场景如下: 要对一篇文档进行实体处理,然后再对实体进行匹配。在这个过程当中,涉及到了好几部分服务: 1 实体识别服务2 数据库查询服务3 es查询服务 整个处理包成了服…...

【安全靶场】-DC-7
❤️博客主页: iknow181 🔥系列专栏: 网络安全、 Python、JavaSE、JavaWeb、CCNP 🎉欢迎大家点赞👍收藏⭐评论✍ 一、收集信息 1.查看主机是否存活 nmap -T4 -sP 192.168.216.149 2.主动扫描 看开放了哪些端口和功能 n…...

0065__windows开发要看的经典书籍
windows开发要看的经典书籍_window编程书籍推荐-CSDN博客...

第133天:内网安全-横向移动域控提权NetLogonADCSPACKDC永恒之蓝
案例一:横向移动-系统漏洞-CVE-2017-0146 这个漏洞就是大家熟悉的ms17-010,这里主要学习cs发送到msf,并且msf正向连接后续 原因是cs只能支持漏洞检测,而msf上有很多exp可以利用 注意msf不能使用4.5版本的有bug 这里还是反弹权…...

【IoTDB 线上小课 06】列式写入=时序数据写入性能“利器”?
【IoTDB 视频小课】更新来啦!今天已经是第六期了~ 关于 IoTDB,关于物联网,关于时序数据库,关于开源... 一个问题重点,3-5 分钟,我们讲给你听: 列式写入到底是? 上一期我们详细了解了…...

【机器学习】小样本学习的实战技巧:如何在数据稀缺中取得突破
我的主页:2的n次方_ 在机器学习领域,充足的标注数据通常是构建高性能模型的基础。然而,在许多实际应用中,数据稀缺的问题普遍存在,如医疗影像分析、药物研发、少见语言处理等领域。小样本学习(Few-Shot Le…...

2024.08.14 校招 实习 内推 面经
地/球🌍 : neituijunsir 交* 流*裙 ,内推/实习/校招汇总表格 1、校招 | 理想汽车2025“理想”技术沙龙开启报名 校招 | 理想汽车2025“理想”技术沙龙开启报名 2、校招 | 紫光国芯2025校园招聘正式启动 校招 | 紫光国芯2025校园招聘正式…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...









