【3.1】贪心算法-解分发饼干
一、题目
二、解题思路
贪心算法,亦称贪婪算法,是一种在解决问题时始终选择当前状态下最优解的策略。换言之,该算法并不追求全局最优,而是基于局部最优解的累积效果。
在《算法导论》一书中,对贪心算法有如下阐述:贪心算法在每一步都做出当时认为最佳的选择,即始终采取局部最优的决策,期望这些局部最优选择能够导向全局最优解。
针对本题,贪心算法尤为适用。题目要求尽可能多地满足孩子们的需求,由于饼干不可分割,因此我们可以采取一种策略,即让胃口较大的孩子食用较大的饼干,而胃口较小的孩子则食用较小的饼干。具体操作时,可以从胃口最小的孩子开始,尝试用最小的饼干来满足其需求,若无法满足,则逐步尝试更大的饼干,直至找到合适的饼干或遍历完所有饼干。
#include <iostream>
#include <vector>
#include <algorithm>int findContentChildren(std::vector<int>& g, std::vector<int>& s) {// 先对胃口值和饼干尺寸进行排序std::sort(g.begin(), g.end());std::sort(s.begin(), s.end());int count = 0;for (int j = 0; count < g.size() && j < s.size(); j++) {// 如果当前饼干能满足当前孩子的胃口值,count就加1,否则就继续查找更大的饼干if (g[count] <= s[j])count++;}return count;
}int main() {std::vector<int> g = {1, 2, 3}; // 孩子的胃口值std::vector<int> s = {1, 1}; // 饼干的尺寸int result = findContentChildren(g, s);std::cout << "满足的孩子数量: " << result << std::endl;return 0;
}三、代码实现
#include <iostream>
#include <vector>
#include <algorithm>int findContentChildren(std::vector<int>& g, std::vector<int>& s) {// 先对胃口值和饼干尺寸进行排序std::sort(g.begin(), g.end());std::sort(s.begin(), s.end());int count = 0;int i = s.size() - 1;for (int j = g.size() - 1; i >= 0 && j >= 0; j--) {// 如果当前饼干能满足当前孩子的胃口值,count就加1,否则就继续查找胃口更小的孩子if (g[j] <= s[i]) {count++;i--;}}return count;
}int main() {std::vector<int> g = {1, 2, 3}; // 孩子的胃口值std::vector<int> s = {1, 1}; // 饼干的尺寸int result = findContentChildren(g, s);std::cout << "满足的孩子数量: " << result << std::endl;return 0;
}相关文章:

【3.1】贪心算法-解分发饼干
一、题目 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是, 每个孩子最多只能给一块饼干 。 对每个孩子i,都有一个 胃口值 g[i] ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干j,都有一个…...
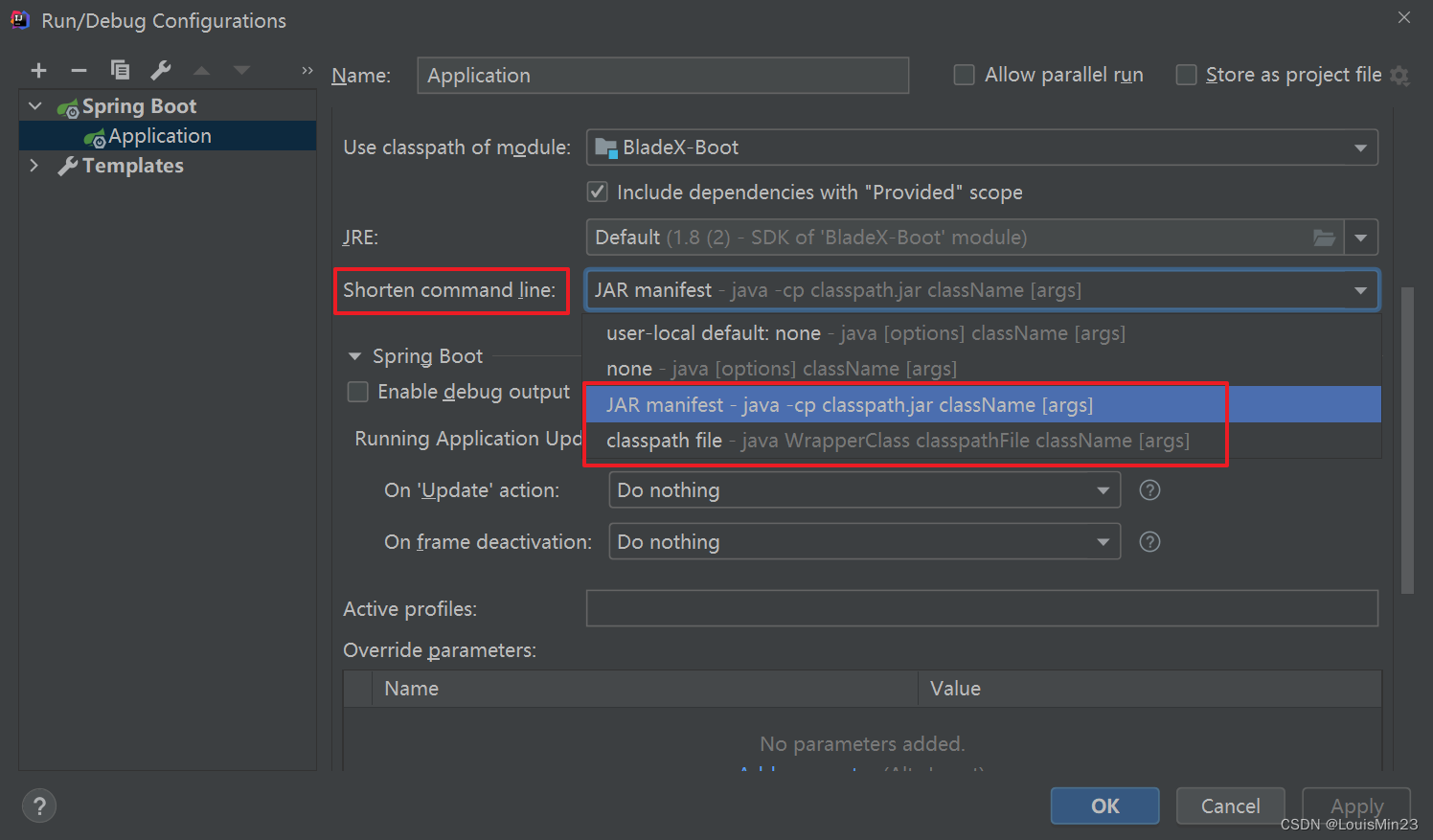
解决 Error running ‘Application‘: Command line is too long.
一、项目场景: 运行刚拉取下来的项目代码,出现下面问题描述的错误提示。 二、问题描述 Error running Application: Command line is too long. Shorten command line for Application or also for Spring Boot default configuration? 翻译翻译&…...

衡量与归因将是Netflix程序化广告业务的首要任务
作者:刀客doc 8月20日,Netflix宣布今年上半年,品牌的招商收入同比增长了150%,广告主来自旅游、汽车、零售商、快餐和大众快消等行业。这一消息提振了资本市场对Netflix广告业务的信心,8月20日收盘创下每股 698.54 美元…...

关于如何在已有qt项目中添加该项目的单元测试工程
关于如何在已有qt项目中添加该项目的单元测试工程 新建一个子目录工程,把已有项目作为子工程添加进去,然后新建单元测试工程也作为子工程添加进去。单元测试项目要独立于实际项目工程,确保去掉测试项目后,实际项目仍可以正常运行…...

深度剖析数字媒体产业链的无限潜力与创新生态
在当今信息爆炸的时代,数字媒体产业链正以势不可挡的姿态展现出其令人瞩目的无限潜力与创新生态。 数字媒体的发展潜力简直无可限量。从在线视频的爆发式增长,到虚拟现实和增强现实技术带来的沉浸式体验,再到社交媒体平台上丰富多彩的内容创…...

集团数字化转型方案(十二)
集团数字化转型方案致力于通过构建一个集成化的数字平台,全面应用大数据分析、人工智能、云计算和物联网等前沿技术,推动业务流程、管理模式和决策机制的全面升级。该方案将从业务流程的数字化改造开始,优化资源配置,提升运营效率…...

Andrid异步更新UI:Handler(二)深入了解:Message你真的会创建?它是如何子线程和主线程通知?
目录 为什么会有HandlerHandler的原理,以及对象讲解主线程的loop在哪里,为什么主线程loop没有阻塞呢?Looper如何保证唯一Handler为什么会引发内存泄漏呢?Message应该如何创建它? 一、为什么会有Handler 线程分为主线…...

2025计算机毕设50条小众好做的Java题目【计算机毕设选题推荐】
随着2025年的到来,计算机专业的学生们又迎来了毕业设计的关键时刻。对于大多数学生来说,选择一个合适的毕业设计题目往往是一项艰巨的任务。本文旨在为那些正在为毕业设计题目烦恼的同学们提供一些灵感和建议,特别是针对使用Java技术栈的同学…...

day06_算法训练
一. Stream流 1.1 Stream流概述 概念: jdk1.8以后提供的新的API, 主要用于批量操作数据(集合的另外一种操作方式),代码非常简洁 流式处理思想: 2.2 Stream对象获取 1.单列集合的Stream流对象获取 2.双列集合的Stream流对象获取 3.数组的Stream流对象获取 4.散装数据的St…...

@SpringBootTest单元测试中报错:无法自动装配,找不到 ‘XXX‘ 类型的 Bean
一开始照着网上教程讲Springboot原理中的代码来copy写的↓ import com.google.gson.Gson; import com.itheima.pojo.Result; import org.junit.jupiter.api.Test; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.boot.test.cont…...
简介、安装、配置、使用)
nodemon学习(一)简介、安装、配置、使用
nodemon用来监视node.js应用程序中的任何更改并自动重启服务,非常适合用在开发环境中。以前,我们开发一个node后端服务时,每次更改文件,均需重启一下,服务才能生效。这使我们的开发效率降低了很多。nodemon的出现,可以…...

【Qt从摄像头视频中获取数据】
有时候需要在视频上画图,所以需要能获取到每一帧视频数据。 以前从视频文件或视频流中得到帧,一般都是使用qt ffmpeg或qt vlc。 qt对显示处理视频大体有以下方法: QMediaPlayer QVideoWidget 这种方法只适合简单的显示视频功能ÿ…...
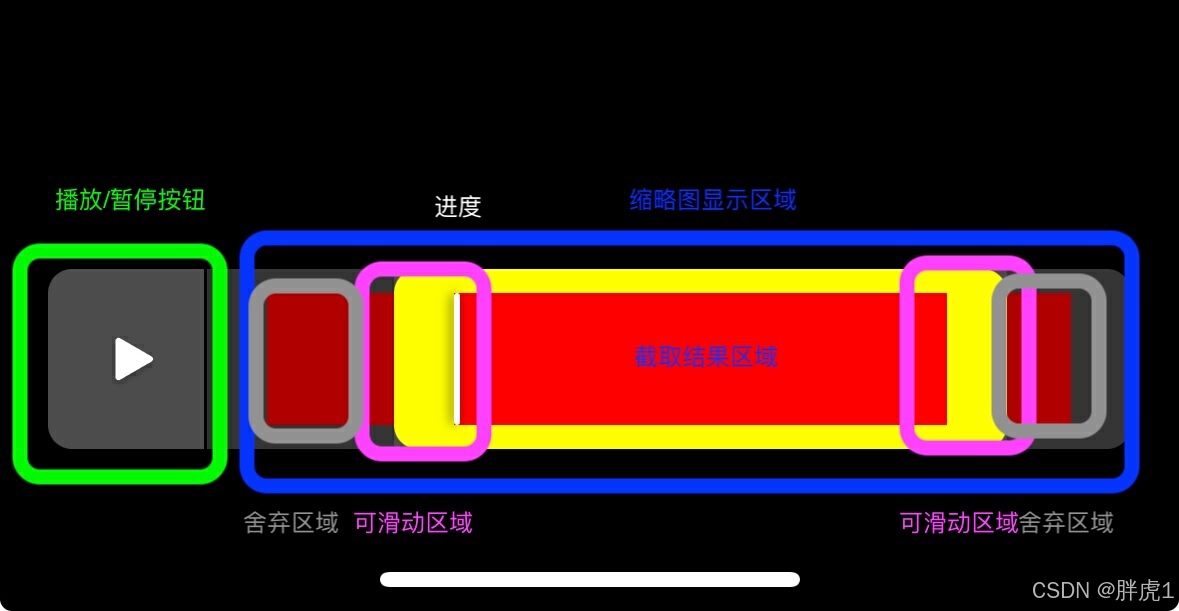
视频截取中的UI小组件
引言 视频截取在社交类 APP 中十分常见。有了上传视频的功能,就不可避免地需要提供截取和编辑的选项。如果我们过度依赖第三方库,项目的代码可能会变得异常臃肿,因为这些库往往包含许多我们用不到的功能,而且它们的 UI 样式和功能…...

java设计模式--结构型模式
结构性模式:适配器模式、桥接模式、装饰模式、组合模式、外观模式、享元模式、代理模式 适配器模式 适配器模式(Adapter Pattern) 充当两个不兼容接口之间的桥梁,属于结构型设计模式。目的是将一个类的接口转换为另一个接口&am…...

消息中间件:Kafka消息丢失与堆积问题分析与解决方案
消息中间件:Kafka消息丢失与堆积问题分析与解决方案 Kafka作为分布式消息系统,广泛应用于实时数据流处理、大数据分析等领域。然而,在实际应用中,Kafka可能会面临消息丢失和消息堆积的问题,这些问题如果得不到有效处理…...

mac终端代理配置指南
终端代理配置指南 在 macOS 中,你可以通过几种不同的方法来配置终端代理。这里介绍两种常见的设置方式:使用 alias 和 shell 函数。 方法 1:使用 Alias 配置代理 打开终端配置文件 默认情况下,macOS 终端使用的是 zsh。如果你的系…...

mbedTLS生成客户端,服务端密钥及CA证书
1. mbedTLS源码:https://github.com/Mbed-TLS/mbedtls.git 2. 生成步骤: 2.1 编译上述源码 2.2 生成CA私钥和自签名证书: 进入编译的build目录,比如:/mbedtls-development/build# 2.2.1生成CA私钥 执行下面的命令&…...

如何有效应对突发技术故障:以网易云音乐为例
引言 在互联网行业,任何一个在线服务都可能遭遇突发的技术故障。这些故障不仅影响用户体验,还可能对公司的品牌形象造成损害。因此,如何快速响应并高效解决这些问题成为了每一个开发团队的重要课题。本文将以网易云音乐在2024年8月19日下午遭…...

上传文件到github仓库
REF: https://blog.csdn.net/litianxiang_kaola/article/details/74075151 已有repository,往仓库里更新内容 点击gitlab里的clone 在git bash中使用git clone,这个时候会将网上的仓库下载到本地,你可以把想要更新的内容直接拖到仓库里 …...

clip-path实现图片边角的裁剪
img {clip-path: polygon(0 7px,7px 0,calc(100% - 20px) 0,100% 20px,100% 100%,16px 100%,0 calc(100% - 16px));}每一个逗号隔开的就是路径坐标 左上角的两个点 0 7px ,7px 0 右上角 calc(100% - 20px) 0,100% 20px 相当于通过这些点练成的线的圈起来的部分就是剩…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
