【超好懂的比赛题解】暨南大学2023东软教育杯ACM校赛个人题解
title : 暨南大学2023东软教育杯ACM校赛 题解
tags : ACM,练习记录
date : 2023-3-26
author : Linno

文章目录
- 暨南大学2023东软教育杯ACM校赛 题解
- A-小王的魔法
- B-苏神的遗憾
- C-神父的碟
- D-基站建设
- E-小王的数字
- F-Uziの真身
- G-电子围棋
- H-二分大法
- I-丁真的小马朋友们
- J-单车运营
- K-超导铁轨
- L-承太郎的"替身数"
暨南大学2023东软教育杯ACM校赛 题解
题目链接:https://ac.nowcoder.com/acm/contest/47948
出题数量:12/12 ,AK了
出题顺序:A->B->C->D->F->G->J->E->I->H->L->K
简评:首先感谢出题组手下留情,再来点中等水平思维题估计就能搞死我了。因为题出的都比较板所以顺理成章地AK了,打搅了大家的做题兴致非常抱歉!这一场如果板子带够了并且刷题量达到一定水平,打得都不会差的。如果觉得自己打得不好,那希望这篇题解能给你带来帮助(不懂也可以继续问),喜欢ACM的话就请继续加油吧!
A-小王的魔法
选某一个数,它的因数都会被选中,因此选它本身肯定是最优的,那么我们直观觉得从大到小枚举的时候把因数都打上标签,然后没打标签的数统计到答案里面就必然是正确的。但可惜n有1e18这样做肯定超时,因此我们继续考虑更直观的结论:
- 当i<=⌊n2⌋i<=\lfloor\frac{n}{2}\rfloori<=⌊2n⌋时,显然有iii的所有因数都包含在2∗i2*i2∗i的所有因数中,因此不必考虑
- 对于i∈[n2,n]i\in [\frac{n}{2},n]i∈[2n,n],没有倍数能够将其包含,所以是最优的,因此答案就是⌈n2⌉\lceil\frac{n}{2}\rceil⌈2n⌉。
void solve(){int n;cin>>n;cout<<(n+1)/2<<"\n";
}
B-苏神的遗憾
注意读题,苏神是可以第一的,但是成绩不能并列。因此一般情况下苏神的成绩是第二名成绩-1秒,但是如果那是第一名的成绩,就要跑得比这个更快一秒才行了。
void solve(){cin>>n;for(int i=1;i<=n;++i) cin>>a[i];stable_sort(a+1,a+1+n);if(a[1]+1==a[2]) ans=a[1]-1;else ans=a[2]-1;cout<<ans<<"\n";
}
C-神父的碟
前置知识:中国剩余定理
原题意也就是让我们解同余方程组:
{x≡b1moda1x≡b2moda2...x≡bnmodan\begin{cases} x\equiv b_1 \mod a_1 \\ x\equiv b_2 \mod a_2 \\ ...\\ x\equiv b_n \mod a_n \\ \end{cases} ⎩⎨⎧x≡b1moda1x≡b2moda2...x≡bnmodan
由于aaa两两互质,令x=(N/ai)∗yx=(N/a_i)*yx=(N/ai)∗y,方程组等同于解同余方程(N/ai)y≡1modai(N/a_i)y\equiv 1 \mod a_i(N/ai)y≡1modai,得到特解yiy_iyi,则方程组的解为:x0=b1x1+b2x2+...+brxrmodNx_0=b_1x_1+b_2x_2+...+b_rx_r \mod Nx0=b1x1+b2x2+...+brxrmodN,在模N意义下唯一。
注意到准备的箱子数aia_iai肯定是不同的质数,也就是说不需要用到扩展CRT,直接套板子即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20;
int n,a[N],b[N],m[N],t[N],M=1;inline int exgcd(int a,int b,int &x,int &y){if(!b){x=1;y=0;return a;}int d=exgcd(b,a%b,y,x);y-=a/b*x;return d;
}inline int inv(int a,int b){int d,x,y;d=exgcd(a,b,x,y);return (x<0)?(x+b):x;
}void solve(){cin>>n;for(int i=1;i<=n;++i){cin>>a[i]>>b[i];M*=a[i]; }int ans=0;for(int i=1;i<=n;++i){m[i]=M/a[i];t[i]=inv(m[i],a[i]);ans+=b[i]*m[i]%M*t[i]%M;ans%=M; }cout<<ans<<"\n";
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T=1;while(T--){solve(); }return 0;
}
D-基站建设
题目给定x,bx,bx,b,我们可以转化为每个节点的做右端点[l,r][l,r][l,r],并且按照rrr从小到大排序,每次贪心地选最右点建基站并跳过已被覆盖掉的节点,即可保证最优。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+7;struct E{int l,r;bool operator <(const E &B)const{return r<B.r;}
}s[N];void solve(){int n;cin>>n;for(int i=1,x,b;i<=n;++i){cin>>x>>b;s[i].l=x-b;s[i].r=x+b;}stable_sort(s+1,s+1+n);int lst=-0x3f3f3f3f,ans=0;for(int i=1;i<=n;++i){if(lst<s[i].l){lst=s[i].r;++ans;}}cout<<ans<<"\n";
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T=1;while(T--){solve(); }return 0;
}
E-小王的数字
前置知识:数位DP
数位DP板题,形式一般都如下:给定L,R,问[L,R]范围内有多少XXX的数,数据范围可出到1e18给定L,R,问[L,R]范围内有多少XXX的数,数据范围可出到1e18给定L,R,问[L,R]范围内有多少XXX的数,数据范围可出到1e18。
流程大概就是按位拆分给的数,然后再按位记忆化搜索统计答案。代码细节各位自己看吧,dfs(stp,zero,lim,mx,now)表示搜到第stp位数,最多连续mx位6,当前连续了now位6时的状态,zero是前置0标签,lim是最高位标签。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=66;int len=0,num[N],vis[N][N][N];int dfs(int stp,bool zero,bool lim,int mx,int now){if(!stp) return (mx>=3);if(!zero&&!lim&&vis[stp][mx][now]) return vis[stp][mx][now];int j=lim?num[stp]:9,ans=0;for(int i=0;i<=j;++i){int tmp=(i==6)?now+1:0;ans+=dfs(stp-1,zero&(i==0),lim&(i==num[stp]),max(mx,tmp),tmp);}if(!zero&&!lim) vis[stp][mx][now]=ans;return ans;
}int solve(int x){len=0;memset(vis,0,sizeof(vis));while(x){num[++len]=x%10;x/=10;}return dfs(len,1,1,0,0);
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int L,R;cin>>L>>R;cout<<solve(R)-solve(L-1)<<"\n";return 0;
}
/*
1 1000000000000000000
*/
F-Uziの真身
看大家的代码写的都好短,我开数组记了前缀和和后缀和。然后枚举‘z’的位置,每个位置对答案的贡献就是前面‘j’的数量乘上后面‘h’的数量,记得取模。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=998244353;
const int N=2e6+7;
int len;
string str;int numj[N],numh[N];void solve(){cin>>len;cin>>str;int ans=0;numj[0]=(str[0]=='j');numh[len]=0;for(int i=1;i<len;++i){numj[i]=numj[i-1]+(str[i]=='j');}for(int i=len-1;i>=0;--i){numh[i]=numh[i+1]+(str[i]=='h');}
// for(int i=0;i<len;++i) cout<<numj[i]<<" "<<numh[i]<<" !!\n";for(int i=1;i<len;++i){if(str[i]=='z') ans+=numj[i-1]*numh[i+1]%mod,ans%=mod;
// cout<<i<<" "<<ans<<" !!\n"; }cout<<ans<<"\n";
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T=1;while(T--){solve(); }return 0;
}/*
14
mjbajzhmuaxing
9
jzhjzhjzh
*/
G-电子围棋
爆搜就行了,首先把最外面一圈全变成1,然后剩下里面的就直接全变成6,最后统计答案即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=55;int n,vis[N][N],mp[N][N];
int xx[]={0,0,-1,1},yy[]={-1,1,0,0};bool check(int x,int y){return (x>=1&&x<=n&&y>=1&&y<=n&&!vis[x][y]&&mp[x][y]==0);}inline void dfs(int x,int y,int id){mp[x][y]=id;vis[x][y]=1;for(int d=0;d<4;++d){int nx=x+xx[d],ny=y+yy[d];if(check(nx,ny)) dfs(nx,ny,id);}
}void solve(){cin>>n;for(int i=1;i<=n;++i){for(int j=1;j<=n;++j) cin>>mp[i][j];}for(int i=1;i<=n;++i){if(!vis[i][1]&&mp[i][1]==0) dfs(i,1,1);if(!vis[i][n]&&mp[i][n]==0) dfs(i,n,1);if(!vis[n][i]&&mp[n][i]==0) dfs(n,i,1); if(!vis[1][i]&&mp[1][i]==0) dfs(1,i,1);}for(int i=1;i<=n;++i){for(int j=1;j<=n;++j){if(!vis[i][j]&&mp[i][j]==0) dfs(i,j,6);}}int ans=0;for(int i=1;i<=n;++i){for(int j=1;j<=n;++j){if(mp[i][j]==6) ++ans; }}cout<<ans<<"\n";
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T=1;while(T--){solve(); }return 0;
}
H-二分大法
没想到这题居然是暴力……大家可以忽略我的做法去看别人的。题目如果不保证所有i累加小于1e7的话,可以考虑建平衡树,我用的是FHQ Treap。这种数据结构可以很方便地进行序列的拆分和合并操作。然后对于拆分之后的两颗平衡树每个节点都有加法标签和乘法标签,仿照线段树的pushdown操作进行先乘后加的处理即可。可能场内没有想我一样写平衡树的同学吧……pushdown真的很坑,让我wa了两发。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+7;
const int mod=1000000007;inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') f=f*-1;ch=getchar();}while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();return x*f;
}int n,q,a[N];
int ch[N][2],val[N],pri[N],sz[N],tg1[N],tg2[N],cnt,rt;void update(int x){sz[x]=1+sz[ch[x][0]]+sz[ch[x][1]];
}
#define mid ((l+r)>>1)
#define ls (ch[x][0])
#define rs (ch[x][1])
void pushdown(int x){if(x&&tg2[x]!=1){if(ls){val[ls]=val[ls]*tg2[x]%mod;tg1[ls]=tg1[ls]*tg2[x]%mod;tg2[ls]=tg2[ls]*tg2[x]%mod; }if(rs){val[rs]=val[rs]*tg2[x]%mod;tg1[rs]=tg1[rs]*tg2[x]%mod;tg2[rs]=tg2[rs]*tg2[x]%mod; }tg2[x]=1;}if(x&&tg1[x]){if(ls) val[ls]=(val[ls]+tg1[x])%mod,tg1[ls]=(tg1[ls]+tg1[x])%mod;if(rs) val[rs]=(val[rs]+tg1[x])%mod,tg1[rs]=(tg1[rs]+tg1[x])%mod;tg1[x]=0;}
}int new_node(int v){sz[++cnt]=1;tg1[cnt]=0;tg2[cnt]=1;val[cnt]=v;pri[cnt]=rand();return cnt;
}int merge(int x,int y){if(!x||!y) return x+y;pushdown(x);pushdown(y);if(pri[x]<pri[y]){ch[x][1]=merge(ch[x][1],y);update(x);return x;}else{ch[y][0]=merge(x,ch[y][0]);update(y);return y;}
}void split(int now,int k,int &x,int &y){if(!now) x=y=0;else{pushdown(now);if(k<=sz[ch[now][0]]) y=now,split(ch[now][0],k,x,ch[now][0]);else x=now,split(ch[now][1],k-sz[ch[now][0]]-1,ch[now][1],y);update(now);}
}int build(int l,int r){if(l>r) return 0;int now=new_node(a[mid]);
// cout<<l<<" "<<r<<" "<<a[mid]<<" !!\n"; ch[now][0]=build(l,mid-1);ch[now][1]=build(mid+1,r);update(now);return now;
}void dfs(int x){if(!x) return;pushdown(x);dfs(ls);printf("%lld ",val[x]%mod);dfs(rs);
}signed main(){ srand(time(0));n=read();for(int i=1;i<=n;++i) a[i]=read()%mod;rt=build(1,n);q=read();for(int i=1,x,op,y,a,b;i<=q;++i){x=read();op=read();y=read();split(rt,x,a,b);if(op==1) val[a]=(val[a]+y)%mod,tg1[a]=(tg1[a]+y)%mod;else val[a]=val[a]*y%mod,tg2[a]=tg2[a]*y%mod;rt=merge(b,a);}dfs(rt);puts("");
}/*
7
1 2 3 4 5 6 7
3
3 1 7
2 1 1
1 2 24
2 5 4 3
04
2 5 4 3
3
1 2 2
3 1 3
1 2 5
——8 7 6 203
0 5 4
3
2 2 5
2 2 3
3 1 7 */
I-丁真的小马朋友们
前置知识:线段树
首先要想到一个很直观的结论就是:我们每次都只选择长度为2的区间可以保证答案是最大的。因此我们只需要维护相邻两项的乘积即可。题目转化为了区间查询最大值和单点修改,学过数据结构的同学可以快速通过。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+7;#define ls (p<<1)
#define rs (p<<1|1)
#define mid ((l+r)>>1)
int n,k,a[N],b[N],mx[N<<2];void build(int p,int l,int r){if(l==r){mx[p]=b[l];return;}build(ls,l,mid);build(rs,mid+1,r);mx[p]=max(mx[ls],mx[rs]);
}void update(int p,int l,int r,int ql,int qr,int k){if(ql<=l&&r<=qr){mx[p]=k;return;}if(ql<=mid) update(ls,l,mid,ql,qr,k);if(qr>mid) update(rs,mid+1,r,ql,qr,k);mx[p]=max(mx[ls],mx[rs]);
}int query(int p,int l,int r,int ql,int qr){if(ql<=l&&r<=qr) return mx[p];int res=0;if(ql<=mid) res=query(ls,l,mid,ql,qr);if(qr>mid) res=max(res,query(rs,mid+1,r,ql,qr));return res;
}void solve(){cin>>n;for(int i=1;i<=n;++i) cin>>a[i];for(int i=1;i<n;++i) b[i]=a[i]*a[i+1];b[n]=b[n-1];build(1,1,n);cin>>k;for(int i=1,op,l,r;i<=k;++i){cin>>op>>l>>r;if(op==1){b[l]=b[l]/a[l]*r;if(l>1) b[l-1]=b[l-1]/a[l]*r; if(l==n) b[n-1]=b[n]; else if(l==n-1) b[n]=b[n-1];a[l]=r;update(1,1,n,n-1,n-1,b[n-1]); update(1,1,n,n,n,b[n]);update(1,1,n,l,l,b[l]);if(l>1) update(1,1,n,l-1,l-1,b[l-1]);}else{cout<<query(1,1,n,l,r-1)<<"\n";}}
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T=1;while(T--){solve(); }return 0;
}
/*
5
1 2 3 4 5
4
2 1 2
2 1 3
2 4 5
2 3 55
1 2 5 3 4
4
2 1 2
2 1 3
2 4 5
2 3 56
2 8 9 1 11 3
6
2 1 5
2 1 3
1 1 10
2 1 2
2 2 3
2 1 36
2 8 9 1 11 3
7
2 1 5
2 1 3
1 6 10
2 1 6
2 5 6
2 4 5
2 4 6
*/
J-单车运营
前置知识:图论基础知识,最小费用最大流
最大流是在一个有向图中从S到T,中间有许多节点,每条边权限制了流量,问单位时间能流过的最大流量是多少的模型。而最小费用最大流流是在这基础上给出每条边每流过一单位水流的费用,问在最大流量的基础上最小费用的模型。显然题目可以套入这个模型,从源点S到每个地点之间的最大流量便是单车最开始的摆放量aia_iai,不造成费用;每两个地点之间的流量无限,即可以不限量的搬运,但是需要造成的费用便是两地的距离disijdis_{ij}disij;每个地点到汇点的流量便是最终要摆放的车辆bib_ibi,也不造成费用。这样,在满足摆放好车辆的前提下(最大流),所需要的努力最少(最小费用)。模型是怎么做到这一点的?去学前置知识。
#include<bits/stdc++.h>
#define int long long
#define inf 0x7f7f7f7f
using namespace std;
const int N=305,M=2e5+7; inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') f=f*-1;ch=getchar();}while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();return x*f;
}inline void write(int x){if(x>9) write(x/10);putchar(x%10+'0');
}int v[M],nxt[M],f[M],cnt=1;
int flow[N],w[M],head[N];inline void addedge(int x,int y,int z,int k){++cnt;v[cnt]=y;w[cnt]=z;f[cnt]=k;nxt[cnt]=head[x];head[x]=cnt;++cnt;v[cnt]=x;w[cnt]=0;f[cnt]=-k;nxt[cnt]=head[y];head[y]=cnt;
}int n,m,S,T;
int dis[N],mcost,mflow;
int inq[N],pre[N];
int mp[N][N],tot=0,q[M*10];inline bool spfa(){for(int i=S;i<=T;++i) dis[i]=inf,inq[i]=0;int L=1,R=1;q[L]=S;inq[S]=1;dis[S]=0;flow[S]=inf;while(L<=R){int fro=q[L];++L;inq[fro]=0;for(int i=head[fro];i;i=nxt[i]){if(w[i]&&dis[v[i]]>dis[fro]+f[i]){dis[v[i]]=dis[fro]+f[i];flow[v[i]]=min(flow[fro],w[i]);pre[v[i]]=i;if(!inq[v[i]]){q[++R]=v[i];inq[v[i]]=1;}}} }return dis[T]!=inf;
}inline void update(){int x=T;while(x!=S){int i=pre[x];w[i]-=flow[T];w[i^1]+=flow[T];x=v[i^1];}mflow+=flow[T];mcost+=flow[T]*dis[T];
}void EK(){while(spfa()) update();
}void solve(){n=read();S=0;T=n+1; for(int i=1;i<=n;++i) addedge(S,i,read(),0);for(int i=1;i<=n;++i) addedge(i,T,read(),0);for(int i=1;i<=n;++i){for(int j=1;j<=n;++j){mp[i][j]=read();addedge(i,j,inf,mp[i][j]);}}EK();write(mcost);
}signed main(){int T=1;while(T--){solve(); }return 0;
}
K-超导铁轨
前置知识:SAM(后缀自动机)
因为被选中的位置不可用,所对于两个字符串S,T来说都可以分段处理。也就是说S的每一段与T的每一段两两匹配,求最长公共子串的最大长度。显然两两匹配会超时,我们不妨对S的每一段字符串建广义SAM,然后枚举T的每一段在SAM上跑最长匹配长度。别问我SAM是怎么做到的(其实就是在DAG上一个一个字符去匹配,如果匹配失败就像KMP一样跳转到Fail的位置),去学前置知识。听说大佬用后缀数组被卡了,可惜。
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+7;int a[N],b[N],lst,tot=1,rt=1,num,ans=0;
int fa[N],len[N],ch[N][30],sz[N][12];
char s[N];
vector<int>G[N];
vector<string>s1,s2;
string str1,str2;void insert(int c,int id){ int p=lst,np=lst=++tot;len[np]=len[p]+1,sz[np][id]++;while(p&&!ch[p][c]) ch[p][c]=np,p=fa[p];if(!p) fa[np]=rt;else{int q=ch[p][c];if(len[q]==len[p]+1) fa[np]=q;else{int nq=++tot;memcpy(ch[nq],ch[q],sizeof(ch[q]));len[nq]=len[p]+1,fa[nq]=fa[q],fa[q]=fa[np]=nq;while(ch[p][c]==q) ch[p][c]=nq,p=fa[p];}}
}void dfs(int x){int len=G[x].size();for(int i=0;i<len;++i){int y=G[x][i];dfs(y);for(int id=1;id<=num;++id) sz[x][id]+=sz[y][id];}
}bool check(int p){ if(!p) return false;for(int i=1;i<=num;++i){if(sz[p][i]) return true;}return false;
}void work(string s){int p=rt,l=0;for(int i=0;i<s.length();++i){int c=s[i]-'a';if(check(ch[p][c])) l++,p=ch[p][c];else{while(p&&!check(ch[p][c])) p=fa[p];if(p) l=len[p]+1,p=ch[p][c];else l=0,p=rt;}ans=max(ans,l);}
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>str1>>str2;int l1=str1.length(),l2=str2.length(),n,m;memset(a,-1,sizeof(a)); memset(b,-1,sizeof(b));cin>>n;for(int i=1;i<=n;++i) cin>>a[i];cin>>m;for(int i=1;i<=m;++i) cin>>b[i];stable_sort(a+1,a+1+n);stable_sort(b+1,b+1+m);
// string tmp="";for(int i=0,j=1;i<l1;++i){if(i==a[j]){if(tmp!="") s1.emplace_back(tmp);++j;tmp="";}else tmp.push_back(str1[i]);}if(tmp!="") s1.emplace_back(tmp);tmp="";for(int i=0,j=1;i<l2;++i){if(i==b[j]){if(tmp!="") s2.emplace_back(tmp);++j;tmp="";}else tmp.push_back(str2[i]);}if(tmp!="") s2.emplace_back(tmp);
// for(auto s:s1){lst=rt;num++;// cout<<s<<" !!\n";for(int i=0;i<s.length();++i) insert(s[i]-'a',num);}for(int i=2;i<=tot;++i) G[fa[i]].emplace_back(i);dfs(rt);for(auto s:s2){ work(s);// cout<<s<<" "<<ans<<" !!\n";}cout<<ans<<"\n";return 0;
} /*
aabaabaab
aa
3
3 6 9
0abcdabcdbacbd
bcd
1
4
1
1*/
L-承太郎的"替身数"
前置知识:数论分块,迪利克雷卷积,莫比乌斯反演
下面是推导过程,如果有不懂的私信我或者去看前置知识。
题意转化为求∑i=1S1∑j=1S2lcm(i,j)\sum_{i=1}^{S1}\sum_{j=1}^{S2}lcm(i,j)∑i=1S1∑j=1S2lcm(i,j),最小公倍数lcm(i,j)=i∗jgcd(i,j)lcm(i,j)=\frac{i*j}{gcd(i,j)}lcm(i,j)=gcd(i,j)i∗j
原式等于∑i=1n∑j=1mi⋅jgcd(i,j)=∑d=1nd⋅∑i=1⌊nd⌋∑j=1⌊md⌋[gcd(i,j)=1]i⋅j=∑d=1n∑d∣in∑d∣jmμ(d)⋅i⋅j令g(n,m)=∑i=1n∑j=1mi⋅j=n⋅(n+1)2×m⋅(m+1)2sum(n,m)=∑d=1nμ(d)⋅d2⋅g(⌊nd⌋,⌊md⌋)原式=∑d=1nd⋅sum(⌊nd⌋,⌊md⌋),可用数论分块和线性筛解决。原式等于 \sum_{i=1}^n\sum_{j=1}^m\frac{i\cdot j}{\gcd(i,j)} \\ = \sum_{d=1}^n d\cdot\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}[\gcd(i,j)=1]\ i\cdot j \\ = \sum_{d=1}^n\sum_{d\mid i}^n\sum_{d\mid j}^m\mu(d)\cdot i\cdot j\\ 令 g(n,m)=\sum_{i=1}^n\sum_{j=1}^m i\cdot j=\frac{n\cdot(n+1)}{2}\times\frac{m\cdot(m+1)}{2} \\ \operatorname{sum}(n,m)=\sum_{d=1}^n\mu(d)\cdot d^2\cdot g(\lfloor\frac{n}{d}\rfloor,\lfloor\frac{m}{d}\rfloor) \\ 原式=\sum_{d=1}^n d\cdot\operatorname{sum}(\lfloor\frac{n}{d}\rfloor,\lfloor\frac{m}{d}\rfloor) ,可用数论分块和线性筛解决。 原式等于i=1∑nj=1∑mgcd(i,j)i⋅j=d=1∑nd⋅i=1∑⌊dn⌋j=1∑⌊dm⌋[gcd(i,j)=1] i⋅j=d=1∑nd∣i∑nd∣j∑mμ(d)⋅i⋅j令g(n,m)=i=1∑nj=1∑mi⋅j=2n⋅(n+1)×2m⋅(m+1)sum(n,m)=d=1∑nμ(d)⋅d2⋅g(⌊dn⌋,⌊dm⌋)原式=d=1∑nd⋅sum(⌊dn⌋,⌊dm⌋),可用数论分块和线性筛解决。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+7;
const int N=1e7+7;int np[N],pri[N],mu[N],sum[N],cnt=0;
void init(){mu[1]=np[1]=1;for(int i=2;i<N;++i){if(!np[i]) pri[++cnt]=i,mu[i]=-1;for(int j=1;j<=cnt&&pri[j]*i<N;++j){np[pri[j]*i]=1;if(i%pri[j]) mu[i*pri[j]]=-mu[i];else break;}}for(int i=1;i<N;++i) sum[i]=(sum[i-1]+i*i%mod*(mu[i]+mod)%mod)%mod;
} int Sum(int x,int y){return (x*(x+1)/2%mod)*(y*(y+1)/2%mod)%mod;
}int func(int x,int y){int res=0;for(int l=1,r;l<=min(x,y);l=r+1){r=min(x/(x/l),y/(y/l));res=(res+(sum[r]-sum[l-1]+mod)*Sum(x/l,y/l)%mod)%mod;}return res;
}int Solve(int x,int y){int res=0;for(int l=1,r;l<=min(x,y);l=r+1){r=min(x/(x/l),y/(y/l));res=(res+(r-l+1)*(l+r)/2%mod*func(x/l,y/l)%mod)%mod;}return res;
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);init();int t,n,m;cin>>t;while(t--){cin>>n>>m;cout<<Solve(n,m)<<"\n"; }return 0;
}
/*
2
4 5
4 5
*/
相关文章:

【超好懂的比赛题解】暨南大学2023东软教育杯ACM校赛个人题解
title : 暨南大学2023东软教育杯ACM校赛 题解 tags : ACM,练习记录 date : 2023-3-26 author : Linno 文章目录暨南大学2023东软教育杯ACM校赛 题解A-小王的魔法B-苏神的遗憾C-神父的碟D-基站建设E-小王的数字F-Uziの真身G-电子围棋H-二分大法I-丁真的小马朋友们J-单车运营K-超…...

go-zero学习及使用中遇到的问题
go-zero学习及使用中遇到的问题1 go-zero入门--单体服务demo1.1 单体服务【官方示例】1.1.1 创建greet服务1.1.2 目录结构1.1.3 编写逻辑1.1.4 启动并访问服务1.2 修改GET入参1.2.1 去除options限制的入参值1.2.2 重启并访问服务1.3 添加post请求【新增方法】1.3.1 修改 greet/…...
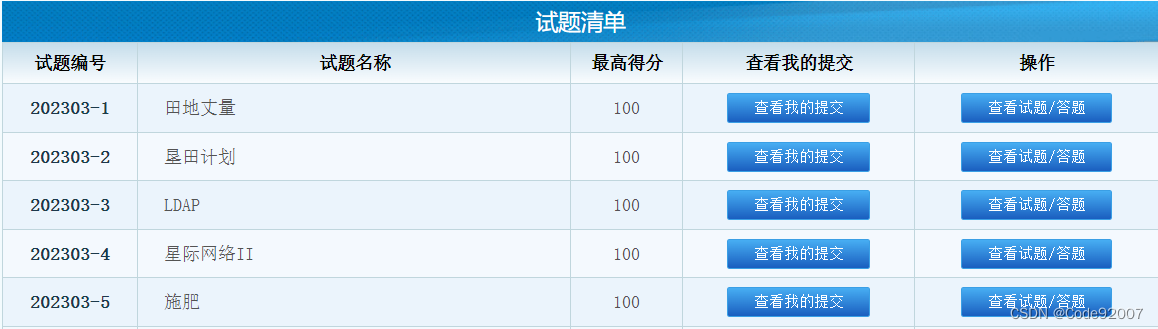
CCF-CSP认证 202303 500分题解
202303-1 田地丈量(矩阵面积交) 矩阵面积交x轴线段交长度*y轴线段交长度 线段交长度,相交的时候是min右端点-max左端点,不相交的时候是0 #include<bits/stdc.h> using namespace std; int n,a,b,ans,x,y,x2,y2; int f(in…...

板内盘中孔设计狂飙,细密间距线路中招
一博高速先生成员:王辉东大风起兮云飞扬,投板兮人心舒畅。赵理工打了哈欠,伸了个懒腰,看了看窗外,对林如烟说道:“春天虽美,但是容易让人沉醉。如烟,快女神节了,要不今晚…...
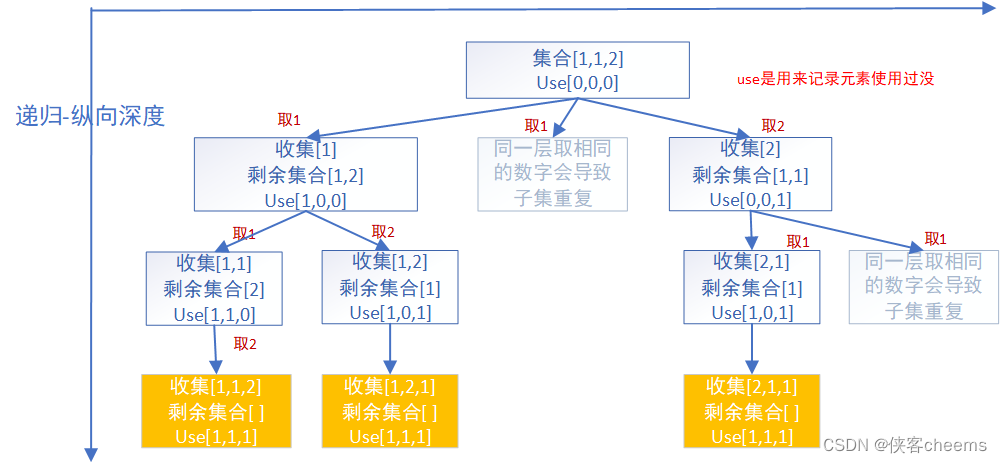
面试热点题:回溯算法 递增子序列与全排列 II
前言: 如果你一点也不了解什么叫做回溯算法,那么推荐你看看这一篇回溯入门,让你快速了解回溯算法的基本原理及框架 递增子序列 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两…...

怎么找回回收站删除的文件
我们都知道,电脑文件都是放在桌面上的,单独存放或者一起存放在文件夹里。但总会有已用完或者是没用的文件,这让我们不得不对其进行清理。而清空回收站也是不可避免的。如果出现了清空文件中还有我们需要的文件,怎么找回回收站删除…...

dp-打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非…...

C++预处理连接
目录定义常量字符串前缀定义枚举类型Boost C库中常常使用预处理连接来定义宏和模板类Google开源的C单元测试框架gtest,使用预处理连接技术创建测试用例和测试方法C预处理连接(Preprocessor Concatenation)是一种宏定义技巧,用于将…...

3、DRF实战总结:基于类的视图APIView, GenericAPIView和GenericViewSet视图集(附源码)
前面介绍了什么是符合RESTful规范的API接口,以及使用了基于函数的视图(FBV)编写了对文章进行增删查改的API。在本篇文章将使用基于类的视图(Class-based View, CBV)重写之前的接口。 参考: 1、Django开发总结:Django MVT与MVC设计模式&…...

AutoSAR PduR -AutoSAR PDU常用的使用方式【发送,接收,网关】
总目录链接==>> AutoSAR入门和实战系列总目录 @学前问答: AutoSAR PDU在哪里全局定义的? AutoSAR PDU涉及到哪些模块? AutoSAR PDU网关怎么使用? 文章目录 1 AutoSAR PDU发送2 AutoSAR PDU接收3 AutoSAR PDU网关转发4 答疑解析AutoSAR PDU 怎么样通过PduR 实现与其…...

瑟瑟发抖吧~OpenAI刚刚推出王炸——引入ChatGPT插件,开启AI新生态
5分钟学会使用ChatGPT 插件(ChatGPT plugins)——ChatGPT生态建设的开端ChatGPT插件是什么OpenAI最新官方blog资料表示,已经在ChatGPT中实现了对插件的初步支持。插件是专门为以安全为核心原则的语言模型设计的工具,可帮助ChatGPT…...

脉诊(切脉、诊脉、按脉、持脉)之法——入门篇
认识脉诊何谓脉诊?脉诊的渊源脉诊重要吗?脉诊确有其事,还是故弄玄虚?中医科学吗?如何脉诊?寸口脉诊法何谓脉诊? 所谓脉诊,就是通过把脉来诊断身体健康状况的一种必要手段。 …...

【十二天学java】day09常用api介绍
1.API 1.1API概述 什么是API API (Application Programming Interface) :应用程序编程接口 java中的API 指的就是 JDK 中提供的各种功能的 Java类,这些类将底层的实现封装了起来,我们不需要关心这些类是如何实现的,只需要学习这…...
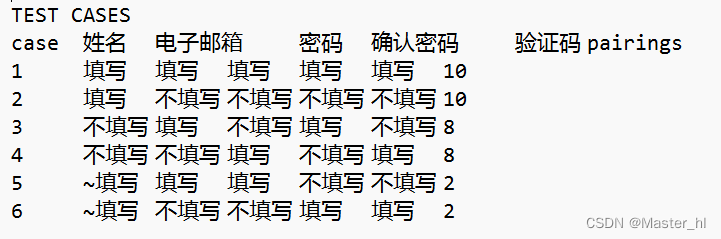
软件测试 - 测试用例常见面试题
1.测试用例的要素测试用例是为了实施测试而向被测试的系统提供的一组集合, 这组集合包含 : 测试环境, 操作步骤, 测试数据, 预期结果等要素.例如 : 在 B 站输入框输入一个空格, 检查结果测试用例标题 : 输入框输入空格测试环境 : Windows 系统, 谷歌浏览器-版本 111.0.5563.65&…...

几种常见的API接口分页方案
文章目录1 概述2 分页方案2.1 基于偏移量2.2 基于游标3 重复数据处理3.1 基于时间3.2 基于热度3.3 基于推荐1 概述 列表是互联网产品中很常见的一种内容排列形式,而且列表的数据集往往成千上万,一次性返回全量数据集的场景几乎不存在,所以出…...

【Object 类的方法】
在 Java 中,所有类都继承了 Object 类,因此 Object 类中的方法可以在所有 Java 对象中使用。下面是 Object 类中的一些常用方法介绍: equals(Object obj): 用于判断两个对象是否相等。默认情况下,该方法比较的是两个对象的地址是…...

留用户、补内容,在线音乐暗战不停
在线音乐在人们的日常生活中扮演着愈发重要的角色,尤其是在面临巨大压力时,人们往往更倾向于通过倾听一段音乐来缓解内心的紧张与焦虑。而随着在线音乐用户数量的增长以及付费意愿的增强,在线音乐行业也实现了稳步发展。 经过多年的发展&…...

python--exec
在Python中,eval和exec都是用来执行动态代码的内置函数,但它们的作用和使用方式有所不同。 eval(): 将字符串作为Python表达式进行求值,并返回结果。 exec(): 将字符串作为Python语句进行执行,没有返回值。 eval()的使用范围通常限…...

干货分享!这6个高效率办公软件,总有一个值得你收藏!
分享6款高效办公软件,可以解决你很多需求,职场人一定要知道。每一款都是精挑细的,可能有的已经很大众了,但肯定还有小伙伴不知道,废话不多说,直接看!! 1、Flomo笔记:记录…...
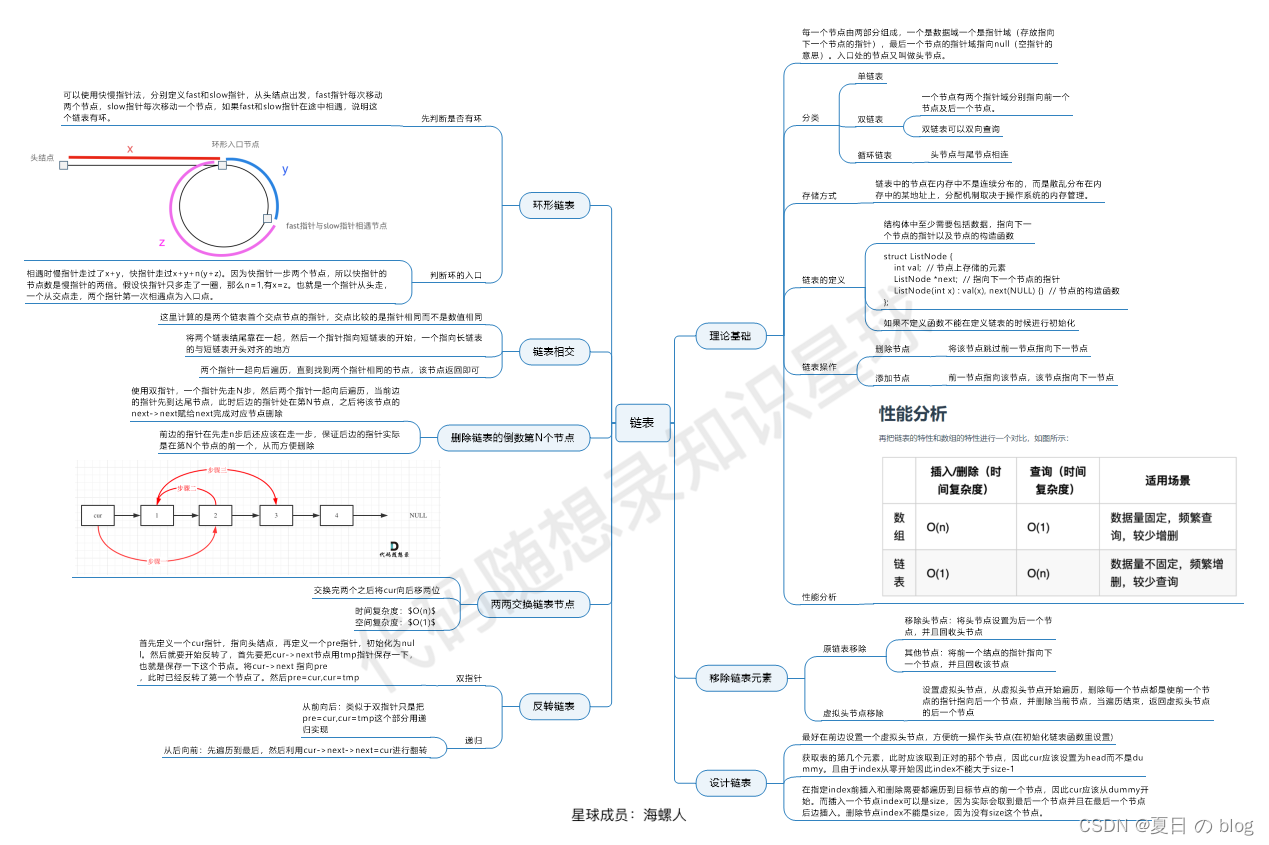
代码随想录刷题-链表总结篇
文章目录链表理论基础单链表双链表循环链表其余知识点链表理论基础单链表双链表循环链表其余知识点移除链表元素习题我的解法虚拟头结点解法设计链表习题我的解法代码随想录代码反转链表习题双指针递归两两交换链表中的节点习题我的解法代码随想录解法删除链表的倒数第N个节点习…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
