字母板上的路径 题解,力扣官方出来挨打(小声)
- 字母板上的路径
我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。
在本题里,字母板为board = [“abcde”, “fghij”, “klmno”, “pqrst”, “uvwxy”, “z”],如下所示。
我们可以按下面的指令规则行动:
如果方格存在,‘U’ 意味着将我们的位置上移一行;
如果方格存在,‘D’ 意味着将我们的位置下移一行;
如果方格存在,‘L’ 意味着将我们的位置左移一列;
如果方格存在,‘R’ 意味着将我们的位置右移一列;
‘!’ 会把在我们当前位置 (r, c) 的字符 board[r][c] 添加到答案中。
(注意,字母板上只存在有字母的位置。)
返回指令序列,用最小的行动次数让答案和目标 target 相同。你可以返回任何达成目标的路径。
这道题在拿到的时候第一眼我想的是把所有字母到另一字母的路径全部通过遍历出来,然后存在一张map里,在通过Map拿,然后拼到答案里,但是这样的开销有些大,因为要做图搜索,且要遍历26*25次,所以图搜索的思路先放弃,绝对不是图搜索学得不好不会写什么的(世上无难事,只要肯放弃)_(:з」∠)_
那么就换个思路,开始找规律吧(早干啥了啊喂)。(╬ ̄皿 ̄)=○#( ̄#)3 ̄)
我们可以发现上面的图就是一个二维数组。以ai为例,a的坐标是[0,0],i的坐标是[1,4],alphabetBoardPath(“i”)=“URRRR!”
也就是说纵向移动,或者说是U和D在答案中的数量取决于ax-ix,横向移动,或者说是U和D在答案中的数量取决于ay-iy。
将a在26个英文字母中的顺序视为0,字母在图表中的x = 他在26个英文字母中的顺序/5(向下取整),y = 他在26个英文字母中的顺序%5。例如z,在字母中的顺序为25,x=25/5=5,y=25%5=0,z的坐标为[5,0]。(心机之蛙一直摸你肚子)
我们将规律转化一下可得一下代码:
public String alphabetBoardPath(String target) {StringBuilder result = new StringBuilder();target = "a" + target;for (int i = 0; i < target.length() - 1; i++) {result.append(returnOperation((Integer) (target.charAt(i) - 'a'), (Integer) (target.charAt(i + 1) - 'a')));}return result.toString();}String returnOperation(int strat, int end) {StringBuilder result = new StringBuilder();int lateralMovement = strat % 5 - end % 5;int longitudinalMovement = strat / 5 - end / 5;for (int i = 0; i < Math.abs(longitudinalMovement); i++) {result.append(longitudinalMovement < 0 ? "D" : "U");}for (int i = 0; i < Math.abs(lateralMovement); i++) {result.append(lateralMovement < 0 ? "R" : "L");}result.append("!");return result.toString();}
然鹅,力扣竟然报错了:
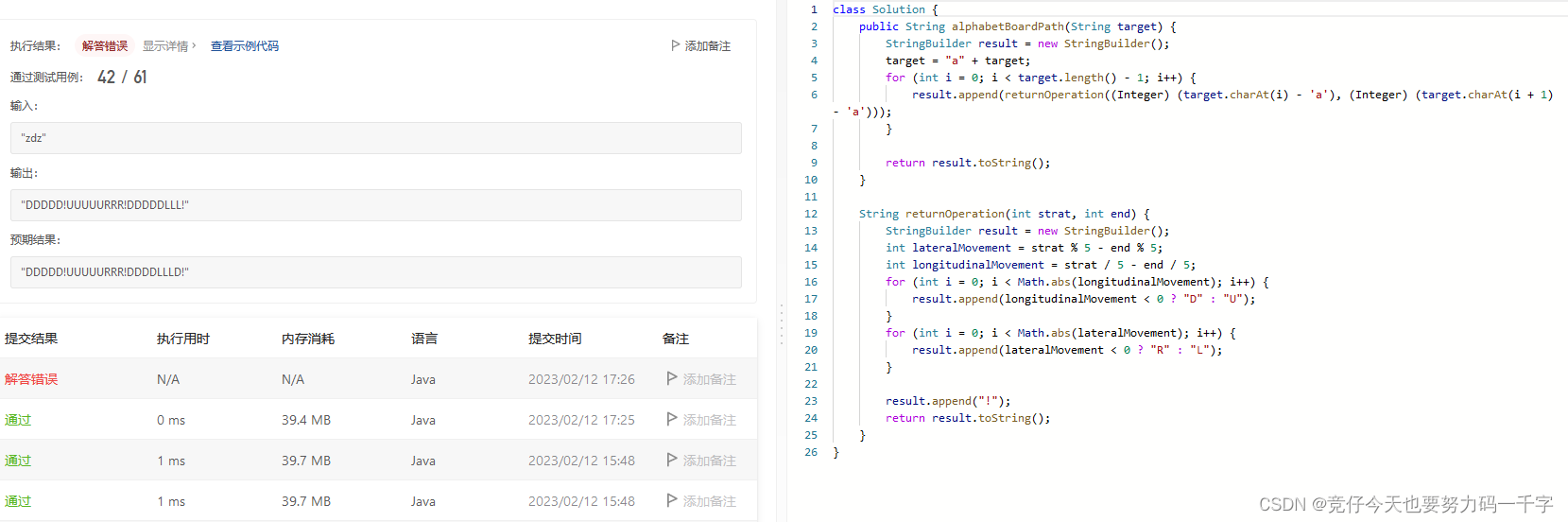
输出:
“DDDDD!UUUUURRR!DDDDDLLL!”
预期结果:
“DDDDD!UUUUURRR!DDDDLLLD!”
我实在是百思不得其解,无论如何都看不出来我为啥错了。(¬‸¬) ?
于是去看了力扣官方给的答案:
public String alphabetBoardPath(String target) {int cx = 0, cy = 0;StringBuilder res = new StringBuilder();for (int i = 0; i < target.length(); i++) {char c = target.charAt(i);int nx = (c - 'a') / 5;int ny = (c - 'a') % 5;if (nx < cx) {for (int j = 0; j < cx - nx; j++) {res.append('U');}}if (ny < cy) {for (int j = 0; j < cy - ny; j++) {res.append('L');}} if (nx > cx) {for (int j = 0; j < nx - cx; j++) {res.append('D');}}if (ny > cy) {for (int j = 0; j < ny - cy; j++) {res.append('R');}} res.append('!');cx = nx;cy = ny;}return res.toString();}作者:LeetCode-Solution
链接:https://leetcode.cn/problems/alphabet-board-path/solution/zi-mu-ban-shang-de-lu-jing-by-leetcode-s-c30t/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
(╯’ - ‘)╯︵ ┻━┻
我猜了一下应该是因为路径的顺序,先赌他一手,按照ULDR的顺序返回。先把桌子摆好┬─┬ ノ(’-'ノ)
改出了以下代码:
public String alphabetBoardPath(String target) {StringBuilder result = new StringBuilder();target = "a" + target;for (int i = 0; i < target.length() - 1; i++) {result.append(returnOperation((Integer) (target.charAt(i) - 'a'), (Integer) (target.charAt(i + 1) - 'a')));}return result.toString();}String returnOperation(int strat, int end) {StringBuilder result = new StringBuilder();int lateralMovement = strat % 5 - end % 5;int longitudinalMovement = strat / 5 - end / 5;for (int i = 0; i < longitudinalMovement; i++) {result.append("U");}for (int i = 0; i < lateralMovement; i++) {result.append("L");}for (int i = 0; i > longitudinalMovement; i--) {result.append("D");}for (int i = 0; i > lateralMovement; i--) {result.append("R");}result.append("!");return result.toString();}
不愧是你啊力扣,题目里说好的 你可以返回任何达成目标的路径。 呢。最后还是要按顺序返回。(╯°Д°)╯︵ ┻━┻
就酱,大家如果有更好的思路请务必和我讨论,下班下班★,°:.☆( ̄▽ ̄)/$:.°★ 。
相关文章:

字母板上的路径 题解,力扣官方出来挨打(小声)
字母板上的路径 我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。 在本题里,字母板为board [“abcde”, “fghij”, “klmno”, “pqrst”, “uvwxy”, “z”],如下所示。 我们可以按下面的指令规则行动:…...
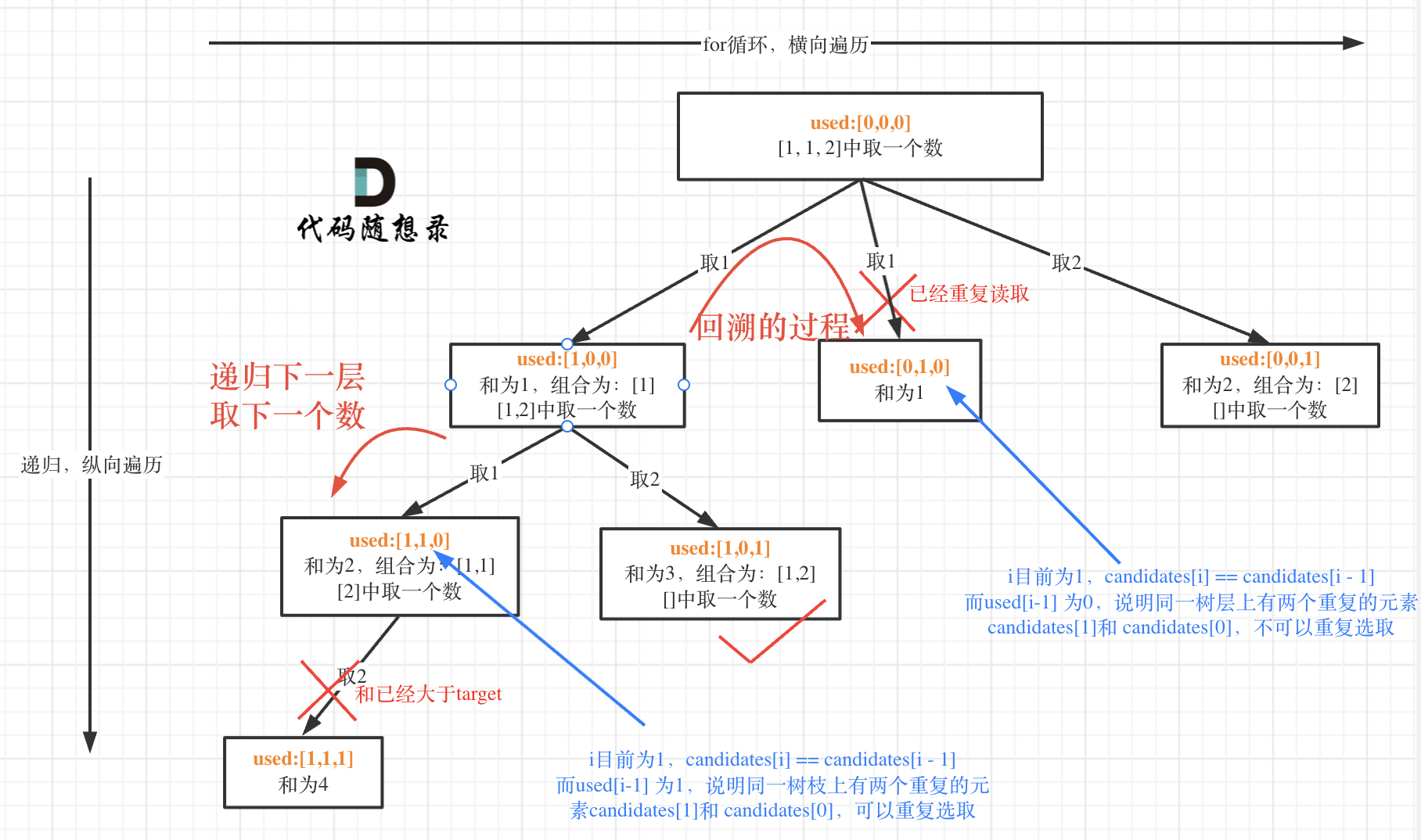
代码随想录算法训练营第二十六天 | 39. 组合总和,40.组合总和II,131.分割回文串
一、参考资料组合总和题目链接/文章讲解:https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html 视频讲解:https://www.bilibili.com/video/BV1KT4y1M7HJ 组合总和II题目链接/文章讲解:https://programmercarl.com/004…...

vueday01-脚手架安装详细
一、vue脚手架安装命令npm i -g vue/cli 或 yarn global add vue/cli安装上面的工具,安装后运行 vue --version ,如果看到版本号,说明安装成功或 vue -V工具安装好之后,就可以安装带有webpack配置的vue项目了。创建项目之前&#…...
)
初识cesium3d(一)
使用ViteVue3.2Cesium。Vite需要Node.js版本14.18及以上版本。Vite命令创建的工程会自动生成vite.config.js文件,来配置一些相关的参数。 1、使用Vite创建vue3项目 # npm npm init vitelatest cesium-app -- --template vue # yarn yarn create vite cesium-app…...

点云转3D网格【Python】
推荐:使用 NSDT场景设计器 快速搭建 3D场景。 在本文中,我将介绍我的 3D 表面重建过程,以便使用 Python 从点云快速创建网格。 你将能够导出、可视化结果并将结果集成到您最喜欢的 3D 软件中,而无需任何编码经验。 此外࿰…...
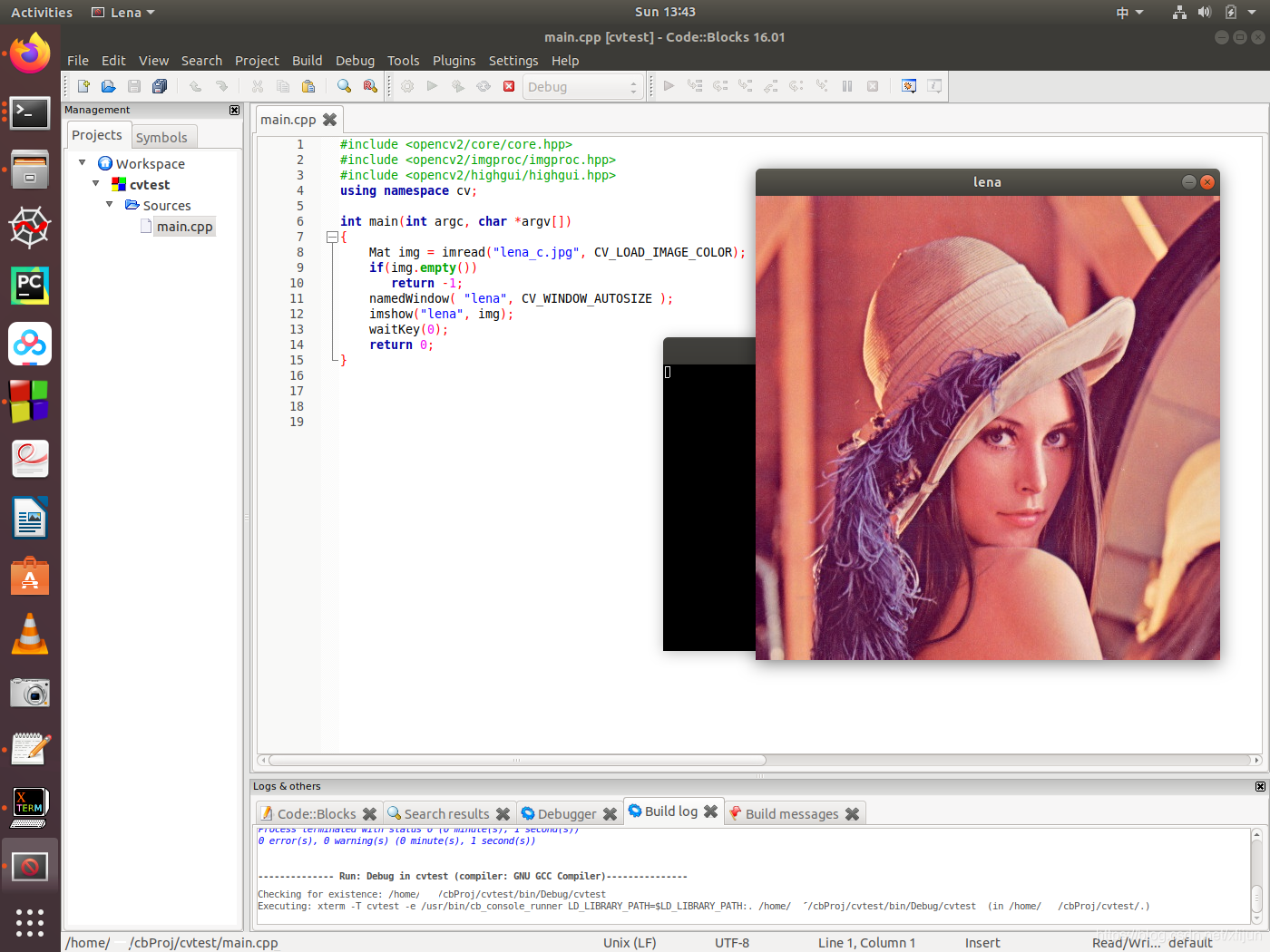
【OpenCV图像处理系列一】OpenCV开发环境的安装与搭建(Ubuntu + Window都适用)
🔗 运行环境:OpenCV,Ubuntu,Windows 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### &#x…...

【代码随想录】-动态规划专题
文章目录理论基础斐波拉契数列爬楼梯使用最小花费爬楼梯不同路径不同路径 II整数拆分不同的二叉搜索树背包问题——理论基础01背包二维dp数组01背包一维数组(滚动数组)装满背包分割等和子集最后一块石头的重量 II目标和一和零完全背包零钱兑换 II组合总和…...

c++数据类型 输入输出
C++语法 //常用包: iostream:cin cout endl cstdio:scanf printf algorithm:max min reverse swap cstring:memset memcpymemset(a,-1,sizeof a) 填充数组memcpy(b,a,sizeof a) 将a数组复制到b数组,长度是a数组字节长度 cmath:sin sqrt pow abs fabs编程是一种控制计…...
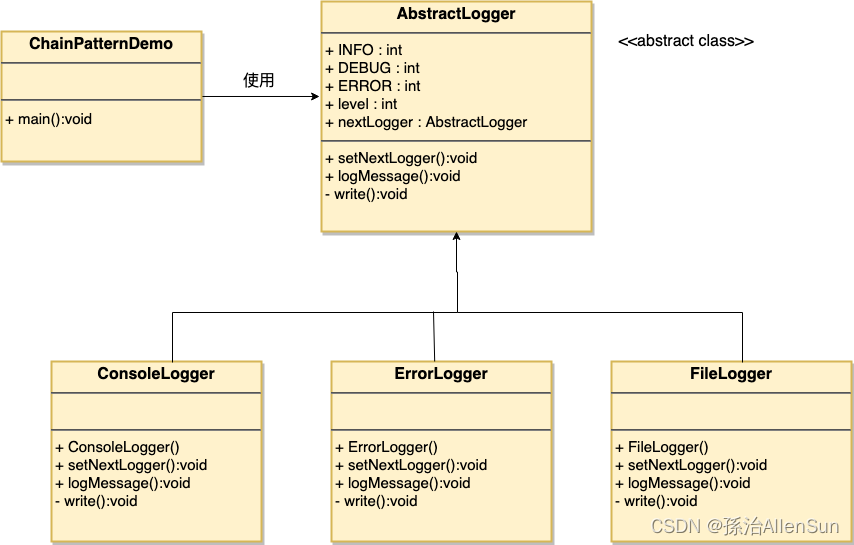
【设计模式-11】责任链模式
认识设计模式(十一)---责任链模式【一】责任链模式【二】介绍(1)意图(2)主要解决(3)何时使用(4)如何解决(5)关键代码(6&am…...
SpringBoot+Vue实现智能物流管理系统
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

【MT7628】MT7628如何修改串口波特率、调试串口物理口、使用UART3口
环境说明 sdk版本:Mediatek_ApSoC_SDK_4320_20150414.tar.bz2 芯片方案:MT7628A Uboot修改串口波特率方法 修改rt2880.h文件 修改include/configs/rt2880.h文件CONFIG_BAUDRATE宏的值 - #define CONFIG_BAUDRATE 57600 +#define CONFIG_BAUDRATE 115200 Kernel中修改串口波特…...

css盒模型介绍
在使用CSS进行网页布局时,我们一定离不开的一个东西————盒子模型。盒子模型,顾名思义,盒子就是用来装东西的,它装的东西就是HTML元素的内容。或者说,每一个可见的 HTML 元素都是一个盒子,下面所说的盒子…...

onetab 谷歌插件历史数据清除
文章目录方法1:测试也可以步骤1:批量执行点击步骤2:python 脚本模拟点击确定操作方法2:成功【推荐】步骤1:修改confirm,类似于hook操作步骤2:批量点击删除操作:onetab 谷歌插件历史数…...

GRBL源码简单分析
结构体说明 GRBL里面的速度规划是带运动段前瞻的,所以有规划运动段数据和微小运动段的区分 这里的“规划运动段”对应的数据结构是plan_block_t,前瞻和加减速会使用到,也就是通过解析G代码后出来的直接直线数据或是圆弧插补出来的拟合直线数据…...
)
第一部分:简单句——第一章:简单句的核心——二、简单句的核心变化(谓语动词的情态)
二、简单句的核心变化 简单句的核心变化其实就是 一主一谓(n. v.) 表达一件事情,谓语动词是其中最重要的部分,谓语动词的变化主要有四种:三态加一否(时态、语态、情态、否定),其中…...

软考高级考试中有五大证书,其中哪个更值得考?
计算机软考属于专业技术人员职业资格水平评价类,是职业资格、专业技术资格(职称)和专业技术水平"三合一"的考试,是目前IT行业仅有的国家级考试。考试不受学历、专业、资历等条件限制。软考高级考试中有五大证书…...

FlexRay™ 协议控制器 (E-Ray)-04
网络管理 累积的网络管理 (NM) 向量位于网络管理寄存器 1 到网络管理寄存器 3 (NMVx (x = 1-3)) 中。【The accrued Network Management (NM) vector is located in the Network Management Register 1 to Network Management Register 3 (NMVx (x = 1-3)).】 网络管理向量 x…...

container_of 根据成员变量获得包含其的对象的地址!
写在前面 本系列文章的灵感出处均是各个技术书籍的读后感,详细书籍信息见文章最后的参考文献 CONTAINER_OF 在书中发现一个很有意思的宏,以此可以衍生出来其很多的用法,这个宏可以根据某个成员变量的地址得到包含这个成员变量地址的对象的…...
Linux进程概念
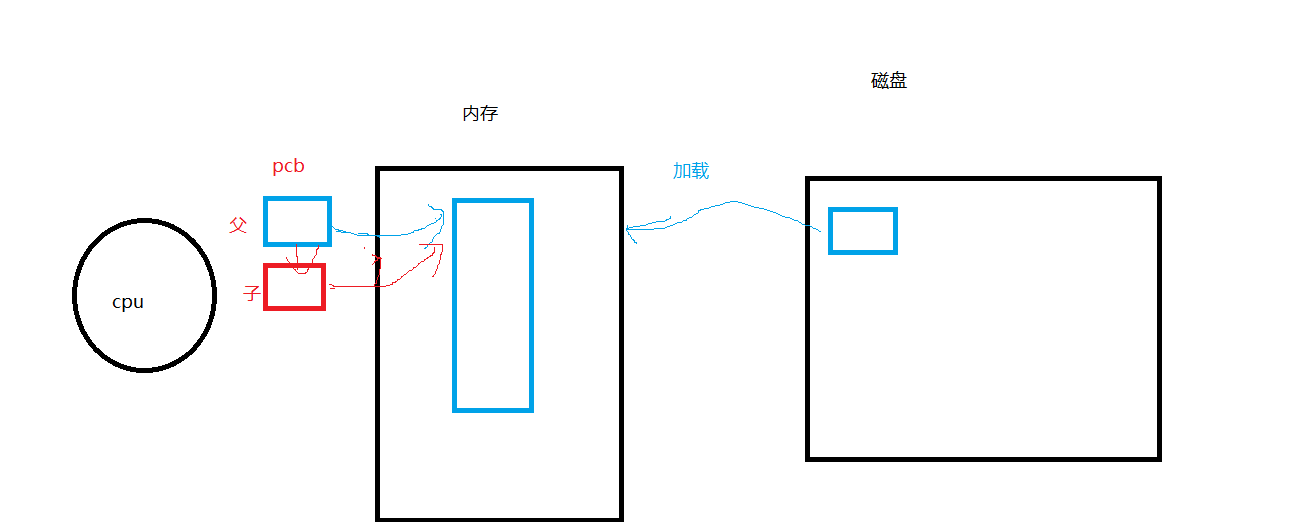
Linux进程概念前言冯诺依曼体系操作系统设计操作系统的目的如何理解OS是一款搞“管理”的软件?系统调用和库函数的概念进程的概念描述进程组织进程查看进程fork()前言 本篇博客主要介绍一些:冯诺依曼体系、OS的理解、进程的一些概…...
算法设计与分析
两个例子:调度问题与投资问题 例1:调度问题 问题 有 n 项任务,每项任务加工时间已知.从 0时刻开始陆续安排到一台机器上加工. 每个任务的完成时间是从 0 时刻到任务加工截止的时间. 求: 总完成时间(所有任务完成时间之和)最短…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

