小游戏也要讲信用
当下,小游戏鱼龙混杂,官方为能更好地保护用户、开发者以及平台的权益,近日宣布7月1日起试行小游戏主体信用分机制。
主体信用分是什么呢?简单来说,这是针对小游戏主体下所有小游戏帐号行为,对开发者进行评级的信用分规则体系。官方希望每个开发者都能合规运营,主动管理和维护自己的信用,做一个负责任的小游戏开发者
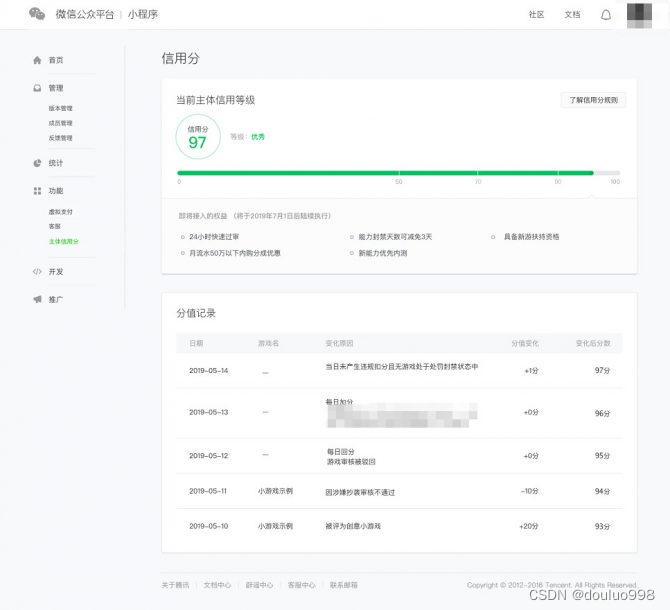
为什么要做主体信用分?
主体信用分旨在鼓励开发者注意每一个小游戏帐号的行为规范,长线布局,按照平台规则合规运营。对于高信用分的主体,平台愿意提供其更多的权益,而信用差时其主体权益也会受到影响。
官方希望通过主体信用分制度能够更好地保护用户、开发者以及平台的权益。开发者可以善用主体信用分规则,主动管理自身信用,维护和争取更多的信用权益。
主体信用分规则是怎样的?
7月1日前,为小游戏主体信用分试运行期。在试运行期间,信用分将根据主体帐号行为进行扣分及回分。希望大家能够充分了解和熟悉帐号行为对主体的影响。7月1日后,将根据主体信用分等级正式陆续执行对应权益。
-
计算范围:主体下的每一个帐号行为都将影响主体信用分计算。
-
扣分行为:小游戏帐号因审核违规或线上处罚,将根据违规性质扣除对应分数。
-
回分行为:当日主体下帐号无审核违规或处罚状态,每日回复1分。
-
额外分数:主体下每认证1款创意游戏,额外增加20分,上限至150分。
具体的规则可详见《主体信用分细则》
主体信用分制度会对小游戏运营带来什么变化?
官方鼓励开发者积极维护自己的信用等级。平台根据主体信用分值分为优秀、一般、信用差、信用极差四个等级。不同等级,将对应不同的权益。
高信用主体享有快速过审、优先参与平台能力内测等权益,而对于屡次违规侵犯用户、其他开发者、平台权益的低信用分主体,平台会对其加以约束。
相关文章:

小游戏也要讲信用
当下,小游戏鱼龙混杂,官方为能更好地保护用户、开发者以及平台的权益,近日宣布7月1日起试行小游戏主体信用分机制。 主体信用分是什么呢?简单来说,这是针对小游戏主体下所有小游戏帐号行为,对开发者进行评…...

贪心算法11
1. 贪心算法的概念 所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。 贪心算法没有固定的算法框架,算法设计的关键是贪心…...
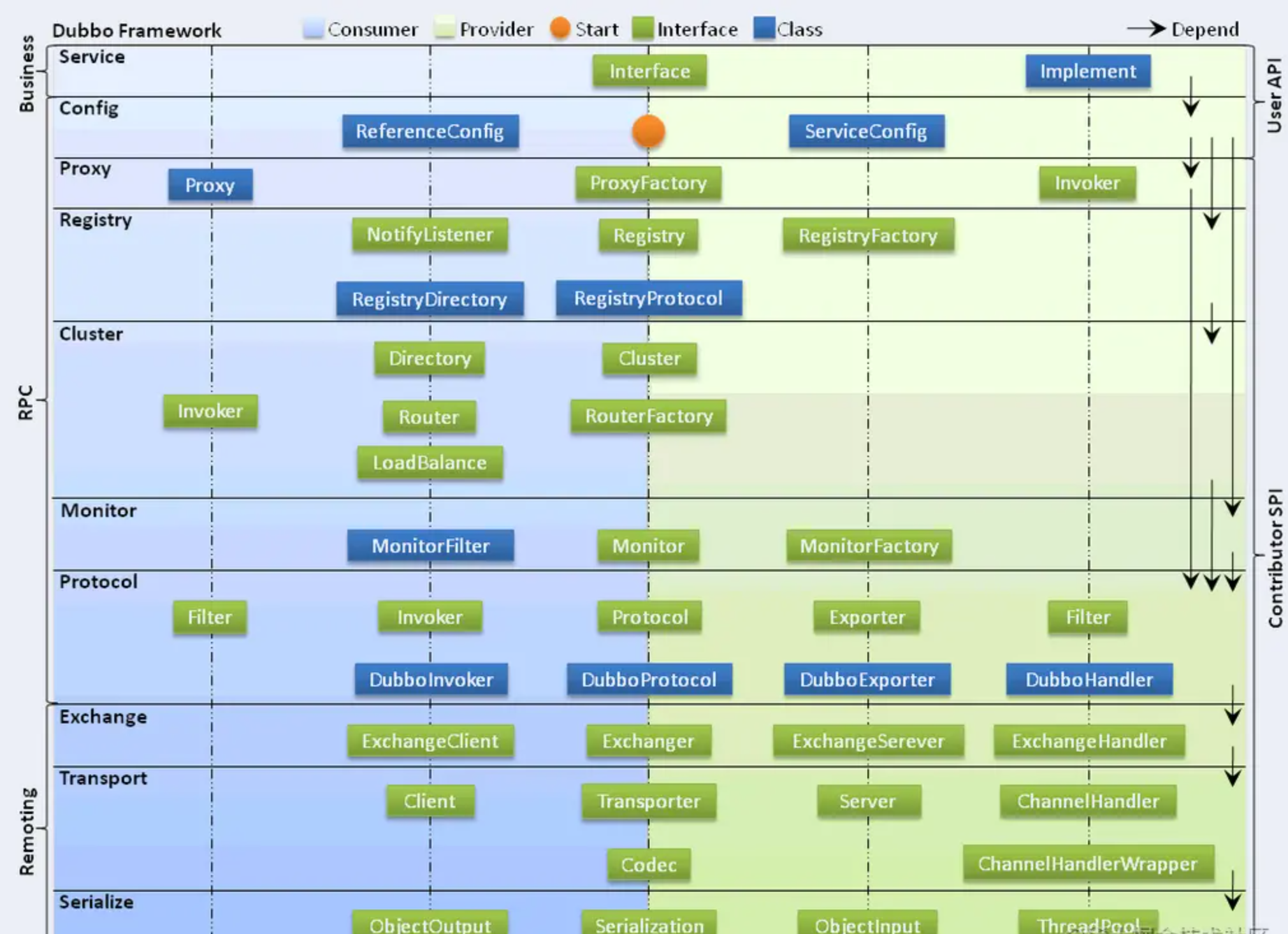
【并发编程】JUC并发编程(彻底搞懂JUC)
文章目录一、背景二、什么是JUC?三、JUC框架结构四、JUC框架概述五、JUC中常用类汇总六、相关名词进程和线程进程线程创建线程的几种常见的方式并发和并行用户线程和守护线程七、synchronized 作用范围:八、Lock锁(重点)什么是 Lock锁类型Lock接口lock()…...

Compose 动画 (七) : 高可定制性的动画 Animatable
1. Animatable和animateDpAsState的区别是什么 Animatable是Android Compose动画的底层API,如果我们查看源码,可以发现animateDpAsState内部是调用的animateValueAsState,而animateValueAsState内部调用的是Animatable animateDpAsState比A…...

vue3组件传值
1.父向子传值 父组件 引入子组件 import Son from ./components/Son.vue 设置响应式数据 const num ref(99) 绑定到子组件 <Son :num"num"></Son> 子组件 引入defineProps import { defineProps } from vue; 生成实例接收数据 type设置接收类…...

小白开发微信小程序00--文章目录
一个小白,一个老牛,空手能不能套白羊,能不能白嫖?我告诉你,一切都so easy,这个系列从0到106,屌到上天,盖过任何一个,试问,网上讲微信小程序开发的,…...
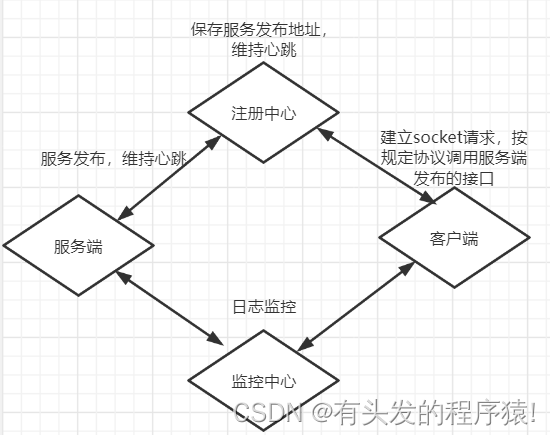
随手记录第九话 -- Java框架整合篇
框架莫过于Spring了,那就以它为起点吧。 本文只为整理复习用,详细内容自行翻看以前文章。 1.Spring 有人说是Spring成就Java,其实也不是并无道理。 1.1 Spring之IOC控制反转 以XML注入bean的方式为入口,定位、加载、注册&…...
电影《铃芽之旅》观后感
这周看了电影《铃芽之旅》,整部电影是新海诚的新作。电影讲述的是女主铃芽为了关闭往门,在日本旅行中,遭遇灾难的故事。 (1)往昔记忆-往昔之物 电影中,有很多的“往门”,换成中国的话说…...
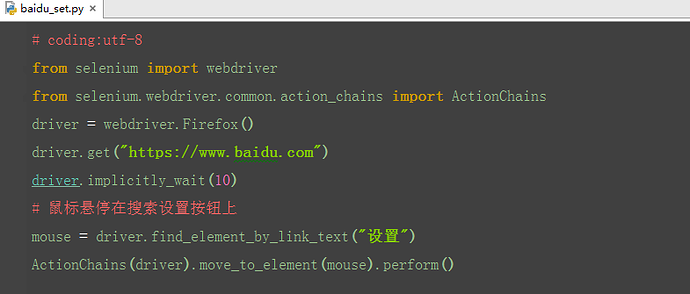
Web自动化测试(二)(全网最给力自动化教程)
欢迎您来阅读和练手!您将会从本章的详细讲解中,获取很大的收获!开始学习吧! 2.4 CSS定位2.5 SeleniumBuilder辅助定位元素2.6 操作元素(键盘和鼠标事件) 正文 2.4 CSS定位 前言 大部分人在使用selenium定…...

【C语言经典例题!】逆序字符串
目录 一、题目要求 二、解题步骤 ①递归解法 思路 完整代码 ②循环解法 思路 完整代码 嗨大家好! 本篇博客中的这道例题,是我自己在一次考试中写错的一道题 这篇博客包含了这道题的几种解法,以及一些我自己对这道题的看法ÿ…...

21 - 二叉树(三)
文章目录1. 二叉树的镜像2. 判断是不是完全二叉树3. 完全二叉树的节点个数4. 判断是不是平衡二叉树1. 二叉树的镜像 #include <ctime> class Solution {public:TreeNode* Mirror(TreeNode* pRoot) {// write code hereif (pRoot nullptr) return pRoot;//这里记得要记得…...

【A-Star算法】【学习笔记】【附GitHub一个示例代码】
文章目录一、算法简介二、应用场景三、示例代码Reference本文暂学习四方向搜索,一、算法简介 一个比较经典的路径规划的算法 相关路径搜索算法: 广度优先遍历(BFC)深度优先遍历(DFC)Di jkstra算法&#…...

纽扣电池澳大利亚认证的更新要求
澳大利亚强制性安全和信息标准草案具体规定了对含有纽扣电池和纽扣电池以 及纽扣电池和纽扣电池本身的消费品的要求, 适用范围 1.本法规适用于: 纽扣锂电池(任何尺寸和类型); 直径为16毫米或以上的纽扣锂电池: 一起提供的纽扣电池(未预先安装在产品中)。 2.但是&…...

零代码零距离,明道云开放日北京站圆满结束
文/麦壁瑜 编辑/李雨珂 2023年3月17日,为期一天的明道云开放日北京站圆满结束。本次开放日迎来超过100名伙伴和客户现场参会,其中不乏安利、通用技术集团、民生银行、迈外迪、DELSK集团、中国人民养老保险、北京汽车等知名企业代表。北京大兴机场、作业…...
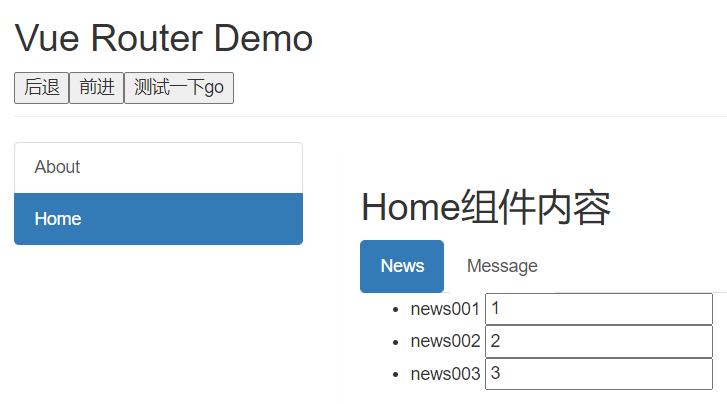
第五章Vue路由
文章目录相关理解vue-router的理解对SPA应用的理解路由的理解基本路由几个注意点嵌套路由——多级路由路由query参数命名路由路由的params参数路由的props配置路由跳转的replace方法编程式路由导航缓存路由组件路由组件独有的生命钩子activated和deactivated路由守卫全局路由守…...
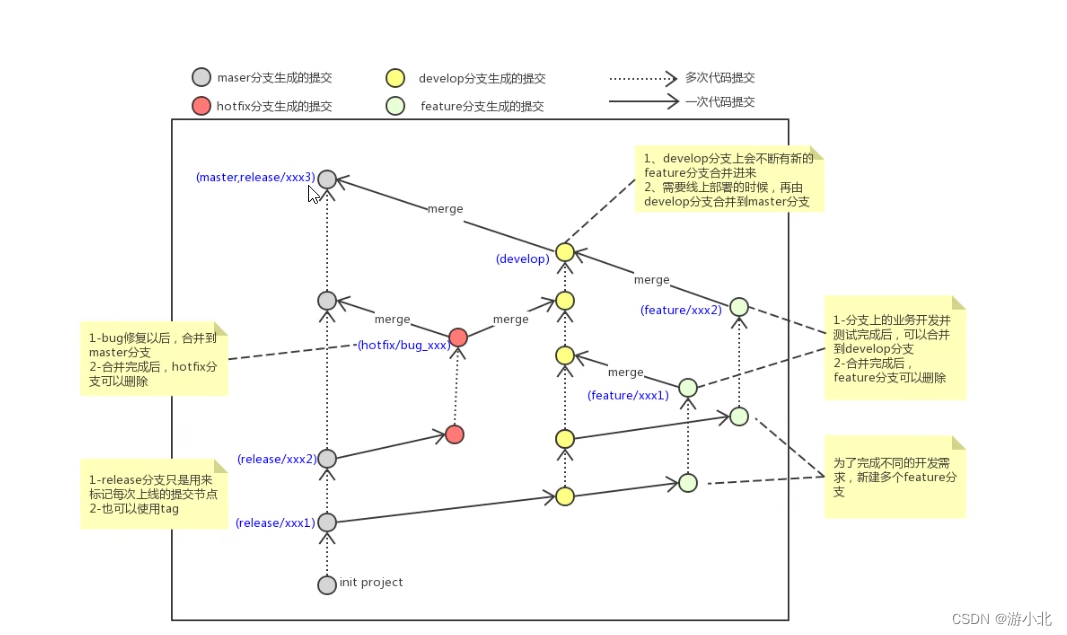
Git常用指令
Git是什么: Git是分布式版本控制系统(Distributed Version Control System,简称 DVCS),分为两种类型的仓库: 本地仓库和远程仓库 第一步先新建仓库,本地 init ,然后提交分枝 链接仓库…...

Java每日一练(20230329)
目录 1. 环形链表 II 🌟🌟 2. 基础语句 ※ 3. 最小覆盖子串 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏 1. 环形…...
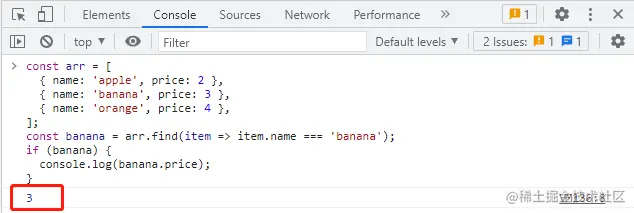
【面试题】JS的一些优雅写法 reduce和map
大厂面试题分享 面试题库 前后端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 web前端面试题库 VS java后端面试题库大全 JS的一些优雅写法 reduce 1、可以使用 reduce 方法来实现对象数组中根据某一key值求和 …...
)
【蓝桥杯真题】包子凑数(裴蜀定理、动态规划、背包问题)
题意 小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。 每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干…...

一种免费将PDF转word的方式
pdf转word的需求对我来说很重要,我经常会有PDF转word的方式,但是网上搜索到的方式,要么收费、要么限制pdf大小或者限制转换次数。这里我分享一种免费转换的方式:用Acrobat Pro 来做转换。Adobe Acrobat Pro拥有强大的功能…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...
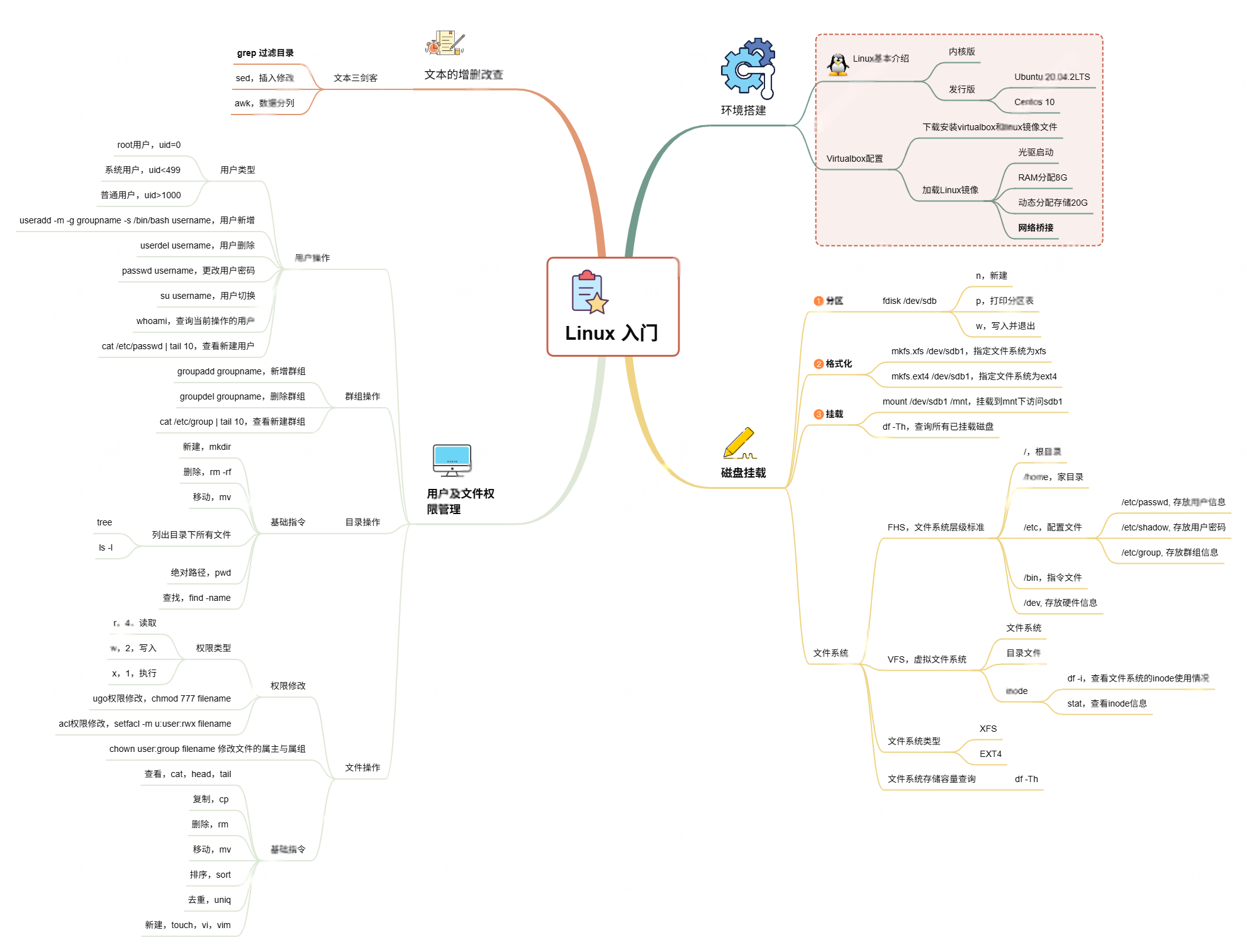
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
