AWGN后验估计下的均值与协方差关系(向量和标量形式)
文章目录
- AWGN信道向量模型
- 后验均值与协方差的关系
- 从实数域拓展到复数域
- 小结
AWGN信道向量模型
考虑一个随机向量x∼pX(x)\boldsymbol x \sim p_{\boldsymbol X}(\boldsymbol x)x∼pX(x),信道模型为
q=x+v,v∼N(0,Σ)\boldsymbol q = \boldsymbol x + \boldsymbol v, \ \ \ \boldsymbol v \sim \mathcal N(\boldsymbol 0, \boldsymbol \Sigma)q=x+v, v∼N(0,Σ)
已知观测值q\boldsymbol qq,将后验估计的均值表示为Fin(q,Σ)=E[x∣q]F_{in}(\boldsymbol q,\boldsymbol \Sigma)=\mathbb E[\boldsymbol x| \boldsymbol q]Fin(q,Σ)=E[x∣q],协方差表示为Ein(q,Σ)=Cov[x∣q]\mathcal E_{in}(\boldsymbol q, \boldsymbol \Sigma)=\text{Cov}[\boldsymbol x| \boldsymbol q]Ein(q,Σ)=Cov[x∣q]。
后验均值与协方差的关系
后验均值Fin(q,Σ)F_{in}(\boldsymbol q,\boldsymbol \Sigma)Fin(q,Σ)与协方差Ein(q,Σ)\mathcal E_{in}(\boldsymbol q, \boldsymbol \Sigma)Ein(q,Σ)满足如下关系式
∂∂qFin(q,Σ)=Ein(q,Σ)Σ−1\frac{\partial}{\partial \boldsymbol q} F_{in}(\boldsymbol q, \boldsymbol \Sigma)= \mathcal E_{in}(\boldsymbol q,\boldsymbol \Sigma) \boldsymbol \Sigma^{-1}∂q∂Fin(q,Σ)=Ein(q,Σ)Σ−1
证明:对Σ>0\boldsymbol \Sigma > \boldsymbol 0Σ>0(正定),定义函数
A0(q)=∫pX(x)ϕ(q−x;Σ)dxA1(q)=∫xpX(x)ϕ(q−x;Σ)dxA2(q)=∫xxTpX(x)ϕ(q−x;Σ)dx\begin{aligned} A_0(\boldsymbol q) &= \int p_{\boldsymbol X}(\boldsymbol x) \phi(\boldsymbol q-\boldsymbol x; \boldsymbol \Sigma) \mathrm{d} \boldsymbol x \\ A_1(\boldsymbol q) &= \int \boldsymbol x p_{\boldsymbol X}(\boldsymbol x) \phi(\boldsymbol q-\boldsymbol x; \boldsymbol \Sigma) \mathrm{d} \boldsymbol x \\ A_2(\boldsymbol q) &= \int \boldsymbol {xx}^T p_{\boldsymbol X}(\boldsymbol x) \phi(\boldsymbol q-\boldsymbol x; \boldsymbol \Sigma) \mathrm{d} \boldsymbol x \\ \end{aligned} A0(q)A1(q)A2(q)=∫pX(x)ϕ(q−x;Σ)dx=∫xpX(x)ϕ(q−x;Σ)dx=∫xxTpX(x)ϕ(q−x;Σ)dx
其中ϕ(q−x;Σ)\phi(\boldsymbol q-\boldsymbol x; \boldsymbol \Sigma)ϕ(q−x;Σ)表示似然分布pQ∣Xp_{\boldsymbol Q|\boldsymbol X}pQ∣X,均值为x\boldsymbol xx协方差为Σ\boldsymbol \SigmaΣ的高斯分布,即
ϕ(q−x;Σ)≡N(x,Σ)\phi(\boldsymbol q-\boldsymbol x; \boldsymbol \Sigma) \equiv \mathcal {N}(\boldsymbol x, \boldsymbol \Sigma)ϕ(q−x;Σ)≡N(x,Σ)
特殊地,先考虑A0(q)A_0(\boldsymbol q)A0(q)
A0(q)=∫pX(x)ϕ(q−x;Σ)dx=∫pX(x)pQ∣X(q∣x)dx=pQ(q)\begin{aligned} A_0(\boldsymbol q) &= \int p_{\boldsymbol X}(\boldsymbol x) \phi(\boldsymbol q-\boldsymbol x;\boldsymbol \Sigma) \mathrm{d} \boldsymbol x \\ &= \int p_{\boldsymbol X}(\boldsymbol x) p_{\boldsymbol Q|\boldsymbol X}(\boldsymbol q| \boldsymbol x) \mathrm{d} \boldsymbol x \\ &= p_{\boldsymbol Q}(\boldsymbol q) \end{aligned} A0(q)=∫pX(x)ϕ(q−x;Σ)dx=∫pX(x)pQ∣X(q∣x)dx=pQ(q)
根据期望的定义,可以写出
Fin(q,Σ)=A1(q)A0(q)F_{in}(\boldsymbol q,\boldsymbol \Sigma) = \frac{A_1(\boldsymbol q)}{A_0(\boldsymbol q)}Fin(q,Σ)=A0(q)A1(q)
根据Cov[w]=E[wwT]−E[w]E[wT]\text{Cov}[\boldsymbol w] =\mathbb E[\boldsymbol w \boldsymbol w^T] - \mathbb E[\boldsymbol w] \mathbb E[\boldsymbol w^T]Cov[w]=E[wwT]−E[w]E[wT],可以写出
Ein(q,Σ)=A2(q)A0(q)−A12(q)A02(q)\mathcal E_{in}(\boldsymbol q,\boldsymbol \Sigma) = \frac{A_2(\boldsymbol q)}{A_0(\boldsymbol q)} - \frac{A^2_1(\boldsymbol q)}{A^2_0(\boldsymbol q)}Ein(q,Σ)=A0(q)A2(q)−A02(q)A12(q)
对高斯分布求导可得
∂∂qϕ(q−x;Σ)=ϕ(q−x;Σ)⋅(x−q)TΣ−1\frac{\partial}{\partial \boldsymbol q} \phi(\boldsymbol q- \boldsymbol x; \boldsymbol \Sigma) = \phi(\boldsymbol q- \boldsymbol x; \boldsymbol \Sigma) \cdot {(\boldsymbol x- \boldsymbol q)}^T \boldsymbol \Sigma^{-1}∂q∂ϕ(q−x;Σ)=ϕ(q−x;Σ)⋅(x−q)TΣ−1
基于此,我们可以得到
∂∂qFin(q,Σ)=∂∂qA1(q)A0(q)=∂A1(q)∂qA0(q)−A1(q)∂A0(q)∂qA02(q)=A2(q)Σ−1A0(q)−A1(q)A1T(q)Σ−1A02(q)=Ein(q,Σ)Σ−1\begin{aligned} \frac{\partial}{\partial \boldsymbol q} F_{in}(\boldsymbol q, \boldsymbol \Sigma) &=\frac{\partial}{\partial \boldsymbol q} \frac{A_1(\boldsymbol q)}{A_0(\boldsymbol q)} \\ &= \frac{ \frac{\partial A_1(\boldsymbol q)}{\partial \boldsymbol q} A_0(\boldsymbol q) - A_1(\boldsymbol q) \frac{\partial A_0 (\boldsymbol q)}{\partial \boldsymbol q} } { A^2_0(\boldsymbol q)} \\ &= \frac{A_2(\boldsymbol q) \boldsymbol \Sigma^{-1}}{A_0(\boldsymbol q)} - \frac{A_1(\boldsymbol q) A^T_1(\boldsymbol q) \boldsymbol \Sigma^{-1}}{A^2_0(\boldsymbol q)} \\ &= \mathcal E_{in}(\boldsymbol q, \boldsymbol \Sigma) \boldsymbol \Sigma^{-1} \end{aligned} ∂q∂Fin(q,Σ)=∂q∂A0(q)A1(q)=A02(q)∂q∂A1(q)A0(q)−A1(q)∂q∂A0(q)=A0(q)A2(q)Σ−1−A02(q)A1(q)A1T(q)Σ−1=Ein(q,Σ)Σ−1
证毕。
从实数域拓展到复数域
考虑一个复随机向量x∼pX(x)\boldsymbol x \sim p_{\boldsymbol X}(\boldsymbol x)x∼pX(x),信道模型为
q=x+v,v∼CN(0,Σ)\boldsymbol q = \boldsymbol x + \boldsymbol v, \ \ \ \boldsymbol v \sim \mathcal {CN}(\boldsymbol 0, \boldsymbol \Sigma)q=x+v, v∼CN(0,Σ)
对于上述推导过程,实数域和复数域的差别于一下两个方面:
- 转置->共轭转置(只是notation的转换)
- 实高斯分布->复高斯分布(主要关注求导)
求导主要体现在
∂∂q∗ϕ(q−x;Σ)=ϕ(q−x;Σ)⋅(x−q)HΣ−1\frac{\partial}{\partial \boldsymbol q^{*}} \phi(\boldsymbol q- \boldsymbol x; \boldsymbol \Sigma) = \phi(\boldsymbol q- \boldsymbol x; \boldsymbol \Sigma) \cdot {(\boldsymbol x- \boldsymbol q)}^H \boldsymbol \Sigma^{-1}∂q∗∂ϕ(q−x;Σ)=ϕ(q−x;Σ)⋅(x−q)HΣ−1
类似地,可以得到复数域的关系表达式为:
∂∂q∗Fin(q,Σ)=Ein(q,Σ)Σ−1\frac{\partial}{\partial \boldsymbol q^{*}} F_{in}(\boldsymbol q, \boldsymbol \Sigma)= \mathcal E_{in}(\boldsymbol q,\boldsymbol \Sigma) \boldsymbol \Sigma^{-1}∂q∗∂Fin(q,Σ)=Ein(q,Σ)Σ−1
小结
AWGN信道向量模型为
q=x+v,x∼pX(x),v∼N(0,Σ)\boldsymbol q = \boldsymbol x + \boldsymbol v, \ \ \ \boldsymbol x \sim p_{\boldsymbol X}(\boldsymbol x), \boldsymbol v \sim \mathcal {N}(\boldsymbol 0, \boldsymbol \Sigma)q=x+v, x∼pX(x),v∼N(0,Σ)
MMSE估计均值与协方差的关系为
-
实数域
∂∂qE[x∣q]=Cov[x∣q]Σ−1\frac{\partial}{\partial \boldsymbol q} \mathbb E[\boldsymbol x| \boldsymbol q] = \text{Cov}[\boldsymbol x| \boldsymbol q] \boldsymbol \Sigma^{-1}∂q∂E[x∣q]=Cov[x∣q]Σ−1 -
复数域(v∼CN(0,Σ)v \sim \mathcal {CN}(\boldsymbol 0, \boldsymbol \Sigma)v∼CN(0,Σ))
∂∂q∗E[x∣q]=Cov[x∣q]Σ−1\frac{\partial}{\partial \boldsymbol q^{*}} \mathbb E[\boldsymbol x| \boldsymbol q] = \text{Cov}[\boldsymbol x| \boldsymbol q] \boldsymbol \Sigma^{-1}∂q∗∂E[x∣q]=Cov[x∣q]Σ−1
退化到标量时,令ν∼N(0,σ2)\nu \sim \mathcal{N}(0, \sigma^2)ν∼N(0,σ2),则
-
实数域
∂∂qE[x∣q]=1σ2var[x∣q]\frac{\partial}{\partial q} \mathbb E[ x| q] = \frac{1}{\sigma^2} \text{var}[ x| q] ∂q∂E[x∣q]=σ21var[x∣q] -
复数域(v∼CN(0,σ2)v \sim \mathcal {CN}(0, \sigma^2)v∼CN(0,σ2))
∂∂q∗E[x∣q]=1σ2var[x∣q]\frac{\partial}{\partial q^{*}} \mathbb E[ x| q] = \frac{1}{\sigma^2} \text{var}[ x| q]∂q∗∂E[x∣q]=σ21var[x∣q]
注意:上述结论不对x\boldsymbol xx的先验分布pX(x)p_{\boldsymbol X}(\boldsymbol x)pX(x)做任何要求。
相关文章:
)
AWGN后验估计下的均值与协方差关系(向量和标量形式)
文章目录AWGN信道向量模型后验均值与协方差的关系从实数域拓展到复数域小结AWGN信道向量模型 考虑一个随机向量x∼pX(x)\boldsymbol x \sim p_{\boldsymbol X}(\boldsymbol x)x∼pX(x),信道模型为 qxv,v∼N(0,Σ)\boldsymbol q \boldsymbol x \boldsymbol v, \…...

Linux常用命令之文件搜索命令
1、常用搜索-find 命令find英文原意find所在路径/bin/find执行权限所有用户功能描述文件搜索语法find [搜索范围] [搜索条件] (默认准确搜索)范例find /etc -name init?? 常用的搜索条件的选项包括: -name:按照文件名进行匹配查找,例&…...

ChatGPT给软件测试行业带来的可能
软件测试在软件开发过程中扮演着至关重要的角色,因为它可以确保软件的质量和可靠性。而随着人工智能技术的不断发展,ChatGPT作为一个强大的自然语言处理工具,可以在软件测试中发挥出许多重要的作用。本文将介绍ChatGPT在软件测试应用中带来的…...

Cadence Allegro 导出Properties on Nets Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Properties on Nets Report作用3,Properties on Nets Report示例4,Properties on Nets Report导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
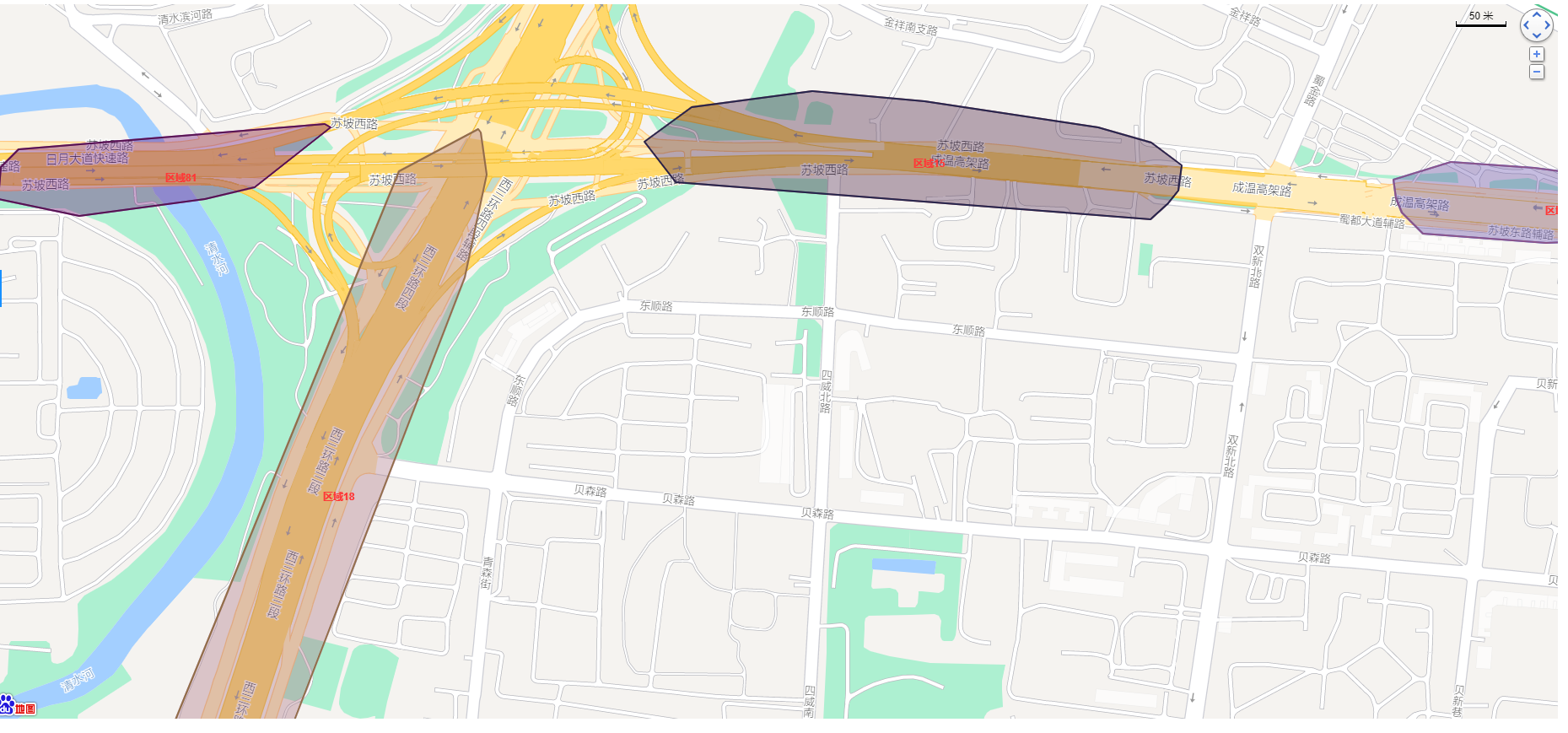
JAVA代码 实现定位数据动态聚集并绘制多边形区域
文章目录思路1、限制聚合距离2、绘制多边形区域3、多边形区域之间合并4、多边形定边点4、逻辑流程一些性能上的优化1、多边形设置圆心2、采用分支合并思路3、清理聚集较分散区域合理性处理1、解决多边形内凹角问题2、解决定边点插入位置问题3、多边形区域扩展成果展示最近有根据…...

基于储能进行调峰和频率调节研究【超线性增益的联合优化】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

体验 Linux 的几个监控命令(htop、nmon、netdata)
体验 Linux 的几个监控命令htopnmonnetdatahtop 安装, sudo dnf install -y htop使用, htopnmon 安装, sudo dnf install -y nmon使用, nmon输入c, 输入C, 输入m, 输入n, 输入…...

NOC大赛2022NOC软件创意编程初赛图形化小低组(小学高年级组)
一、选择题 1.如果要控制所有角色一起朝舞台区右侧移动,下面哪个积太块是不需要的 2.要想让三个角色一起移动起来,下面哪个积木块没有作用 ? 3.小猴按照下面的程序前进,小猴最后一次前进了()步。 4.小可同学写了一个画笔程序画出花朵,但是运行后什么都看不到,不可…...

python进行股票收益率计算和风险控制的实现
股票收益率计算和风险控制的实现 在进行股票投资时,计算收益率和进行风险控制是非常重要的。本文将介绍一个与此相关的函数:radio_day_cal()。 radio_day_cal()函数 def radio_day_cal(last_day, sheet_name, df_dict, code_list, new_list):i 0days…...

自从有了这套近4000页的开发文档后,Java面试路上就像开了挂一样
Java是世界最流行的编程语言,也是国内大多数IT公司的主流语言。招聘网站上Java岗位众多,Java工程师似乎不愁找工作。但仔细一看就会发现,Java岗位的招聘薪酬天差地别,人才要求也是五花八门。而在Java工程师求职过程中,…...

Python文件操作
目录 一、文件操作介绍 二、文件的打开和关闭 三、文件的读写 四、文件文件夹相关操作 五、test 一、文件操作介绍 文件 : python中文件是对象 Liunx 文件 : 一切设备都可以看成是文件 磁盘文件 管道 网络Socket 文件属性: 读 写 执行权限 就是把一些存储存放起来&…...
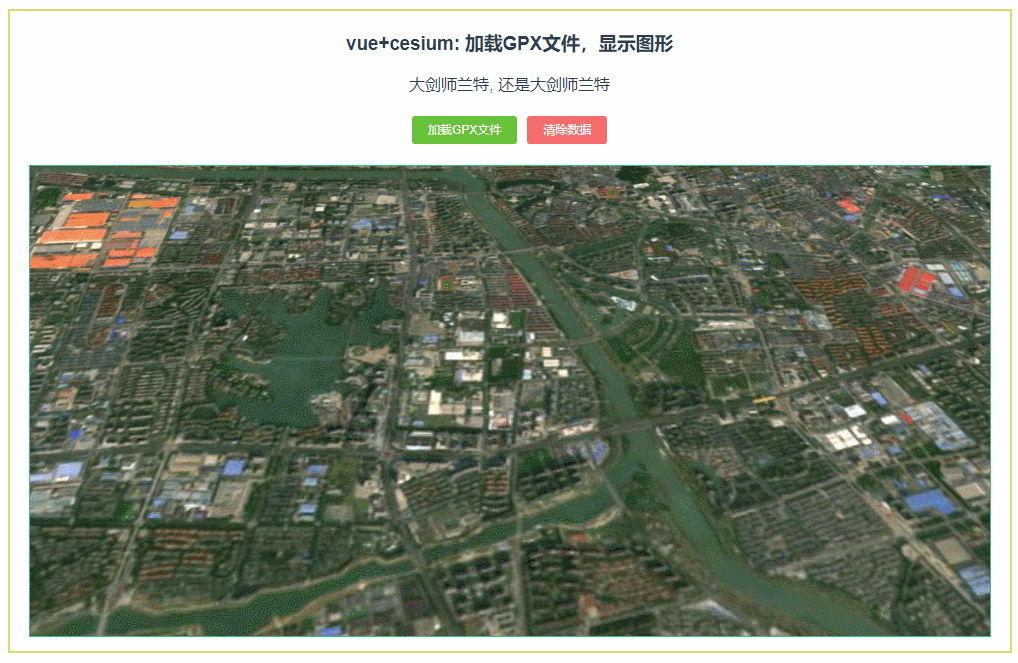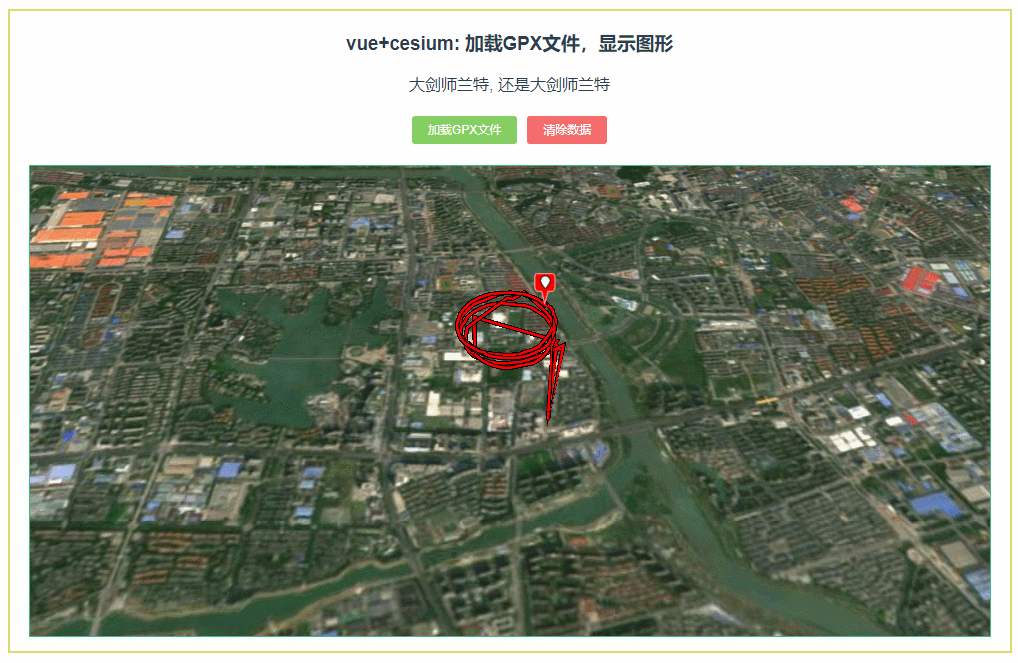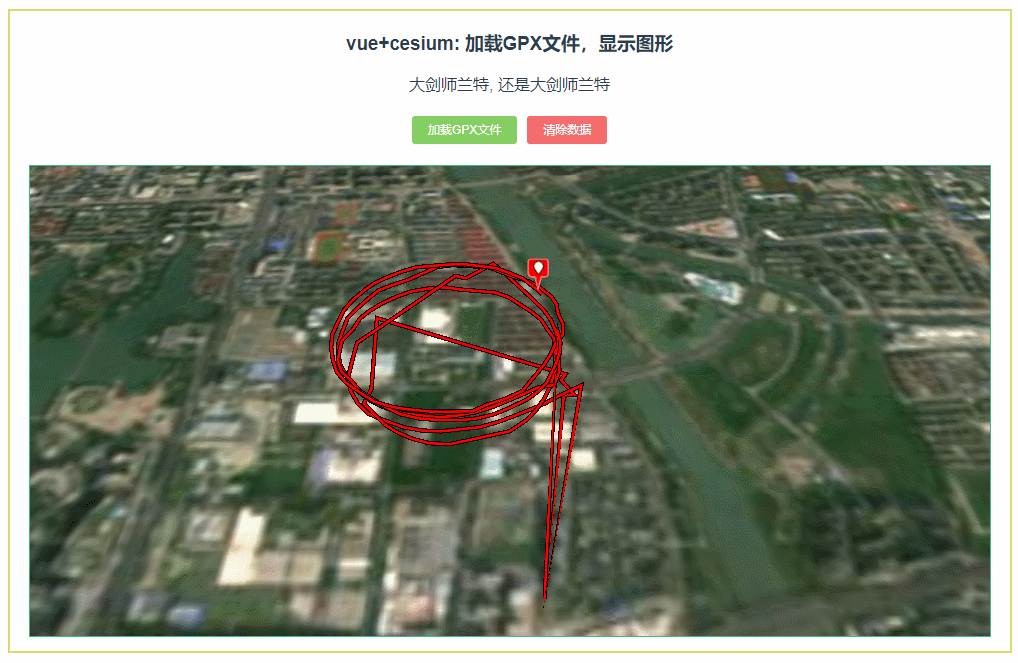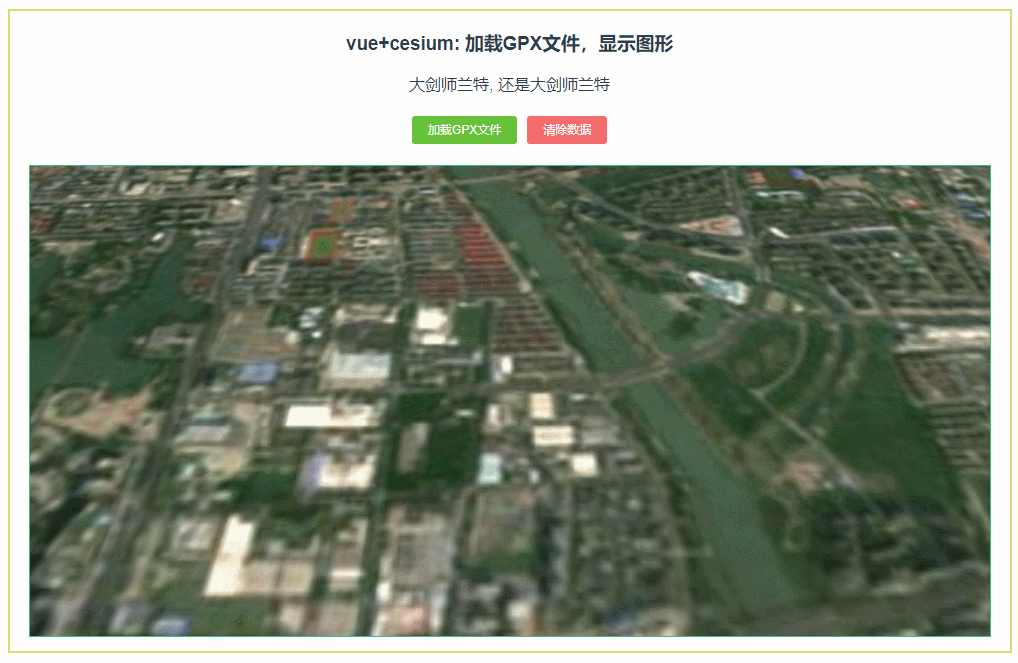
036:cesium加载GPX文件,显示图形
第036个 点击查看专栏目录 本示例的目的是介绍如何在vue+cesium中加载GPX文件, 显示图形。 直接复制下面的 vue+cesium源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共83行)相关API参考:专栏目标示例效果 配置方式 1)查看基础设置:https:/…...
【AI探索】我问了ChatGPT几个终极问题
终于尝试了一把ChatGPT的强大之处,问了一下关心的几个问题: chatGPT现在在思考吗?有没有什么你感兴趣的问题? 你认为AI会对人类产生哪些方面的影响? 你对人类所涉及到的学科有了解吗?你认为在哪些方面与人类…...
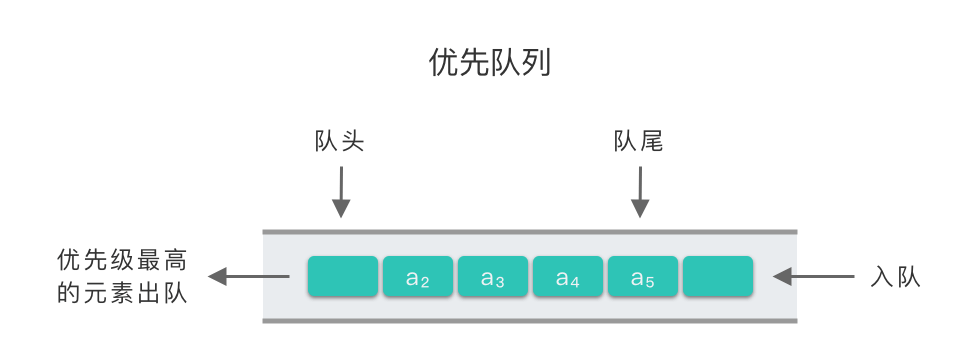
Leetcode 优先队列详解
优先队列 优先队列(Priority Queue):一种特殊的队列。在优先队列中,元素被赋予优先级,当访问队列元素时,具有最高优先级的元素最先删除 普通队列详解Leetcode 队列详解 优先队列与普通队列最大的不同点在于…...

通过两道一年级数学题反思自己
背景 做完这两道题我开始反思自己,到底是什么限制了我?是我自己?是曾经教导我的老师?还是我的父母? 是考试吗?还是什么? 提目 1、正方体个数问题 2、相碰可能性 过程 静态思维: …...

Pytorch :从零搭建一个神经网络
文章目录安装依赖从源码编译pytorchCXX_ABI问题数据集归一化Transforms搭建神经网络Components of a neural networknn.Flattennn.Linearnn.Sequentialnn.SoftmaxModel Parameters优化模型参数设置超参数添加优化循环添加 loss function优化过程完整实现模型的保存和加载安装 …...
)
【华为OD机试 2023最新 】 区块链文件转储系统(C++ 100%)
题目描述 区块链底层存储是一个链式文件系统,由顺序的N个文件组成,每个文件的大小不一,依次为F1,F2,…,Fn。随着时间的推移,所占存储会越来越大。 云平台考虑将区块链按文件转储到廉价的SATA盘,只有连续的区块链文件才能转储到SATA盘上,且转储的文件之和不能超过SATA盘…...

基于springcloud实现分布式架构网上商城演示【项目源码】分享
基于springcloud实现分布式架构网上商城演示摘要 首先,论文一开始便是清楚的论述了系统的研究内容。其次,剖析系统需求分析,弄明白“做什么”,分析包括业务分析和业务流程的分析以及用例分析,更进一步明确系统的需求。然后在明白了系统的需求基础上需要进一步地设计系统,主要包…...

【Qt】(自制类)适用于QTextCharFormat的字体选择对话框
先附上github链接:https://github.com/Ls-Jan/Qt_CharFormatDialog 主要是作为QFontDialog的平替/增强,毕竟Qt自带的字体选择器一言难尽(用过的都叹气)。 【运行界面】 【功能】 一目了然,可以选择字体,设置字号,设置…...
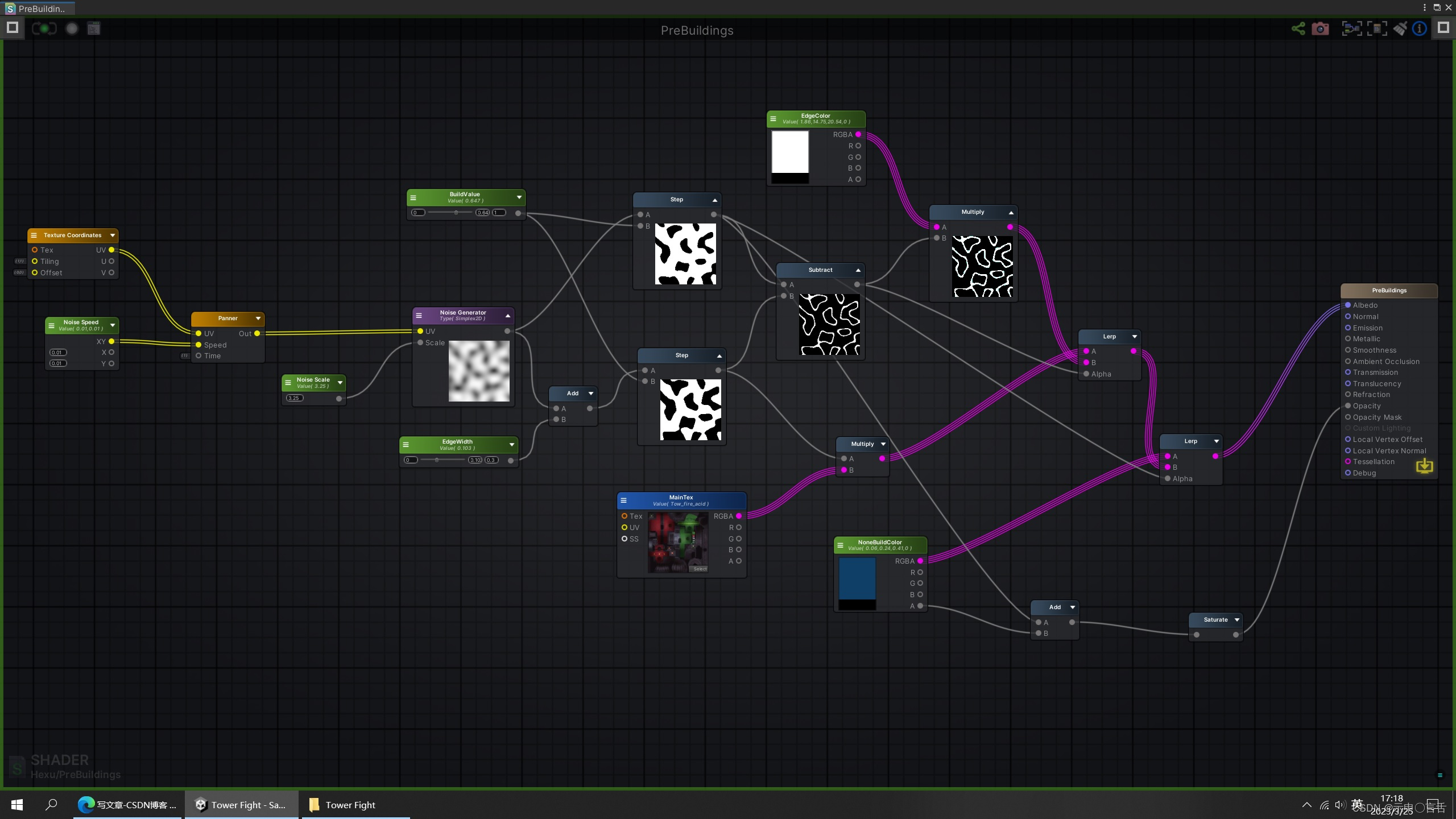
Unity即时战略/塔防项目实战(一)——构造网格建造系统
Unity即时战略/塔防项目实战(一)—— 构造网格建造系统 效果展示 Unity RTS游戏网格建造系统实现原理 地形和格子划分,建造系统BuildManager构建 地形最终需要划分成一个一个的小方格,首先定义一下小方格: private…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
