牛顿迭代法求解x 的平方根
牛顿迭代法是一种可以用来快速求解函数零点的方法。
为了叙述方便,我们用 C C C表示待求出平方根的那个整数。显然, C C C的平方根就是函数
f ( x ) = x c − C f(x)=x^c-C f(x)=xc−C
的零点。
牛顿迭代法的本质是借助泰勒级数,从初始值开始快速向零点逼近。我们任取一个 x 0 x_0 x0作为初始值,在每一步的迭代中,我们找到函数图像上的点 ( x i , f ( x i ) ) (x_i,f(x_i)) (xi,f(xi)) ,过该点作一条斜率为该点导数 f ′ ( x i ) f'(x_i) f′(xi)的直线,与横轴的交点记为 x i + 1 x_{i+1} xi+1 。 x i + 1 x_{i+1} xi+1 相较于 x i x_{i} xi 而言距离零点更近。在经过多次迭代后,我们就可以得到一个距离零点非常接近的交点。下图给出了从 x 0 x_{0} x0 开始迭代两次,得到 x 1 x_{1} x1和 x 1 x_{1} x1的过程。

#include <iostream>
#include <math.h>
int main(int argc, char *argv[]) {const int C = 5;const double y_eps = 1e-10;const double x_eps = 1e-8;double x_n = double(C); // last iteration value x(n)double x_n_1 = (x_n + C / x_n) / 2; // iteration value x(n+1)int iter_num = 1e5; // a protect valuewhile (std::abs(x_n * x_n - C) > y_eps && (std::abs(x_n_1 - x_n) > x_eps) &&(iter_num--)) {x_n = x_n_1;x_n_1 = (x_n + C / x_n) / 2;std::cout<<C<<"的平方根为:"<<x_n_1<<std::endl;}std::cout<<C<<"的平方根最终迭代计算结果为:"<<x_n_1<<std::endl;std::cout<<C<<"的平方根库函数计算结果为:"<<std::sqrt(C)<<std::endl;return 0;
}
计算log:
5的平方根为:2.33333
5的平方根为:2.2381
5的平方根为:2.23607
5的平方根为:2.23607
5的平方根为:2.23607
5的平方根最终迭代计算结果为:2.23607
5的平方根库函数计算结果为:2.23607
参考
youtube
leetcode
相关文章:

牛顿迭代法求解x 的平方根
牛顿迭代法是一种可以用来快速求解函数零点的方法。 为了叙述方便,我们用 C C C表示待求出平方根的那个整数。显然, C C C的平方根就是函数 f ( x ) x c − C f(x)x^c-C f(x)xc−C 的零点。 牛顿迭代法的本质是借助泰勒级数,从初始值开始快…...

端口隔离配置的实验
端口隔离配置是一种网络安全技术,用于在网络设备中实现不同端口之间的流量隔离和控制。以下是对端口隔离配置的详细解析: 基本概念:端口隔离技术允许用户将不同的端口加入到隔离组中,从而实现这些端口之间的二层数据隔离。这种技…...

洛谷 P10456 The Pilots Brothers‘ refrigerator
[Problem Discription] \color{blue}{\texttt{[Problem Discription]}} [Problem Discription] 给定一个 4 4 4 \times 4 44 的网格,每个网格有 0 , 1 0,1 0,1 两种状态。求最少可以通过多少次操作使得整个网格全部变成 1 1 1。 每次操作你需要选定一个格点 …...

windows+vscode+arm-gcc+openocd+daplink开发arm单片机程序
windowsvscodearm-gccopenocddaplink开发arm单片机程序,脱离keil。目前发现的最佳解决方案是,使用vscodeembedded ide插件。 Embedded IDE官方教程文档...

Mysql梳理10——使用SQL99实现7中JOIN操作
10 使用SQL99实现7中JOIN操作 10.1 使用SQL99实现7中JOIN操作 本案例的数据库文件分享: 通过百度网盘分享的文件:atguigudb.sql 链接:https://pan.baidu.com/s/1iEAJIl0ne3Y07kHd8diMag?pwd2233 提取码:2233 # 正中图 SEL…...

24.9.27学习笔记
Xavier初始化,也称为Glorot初始化,是一种在训练深度神经网络时用于初始化网络权重的策略。它的核心思想是在网络的每一层保持前向传播和反向传播时的激活值和梯度的方差尽可能一致,以避免梯度消失或梯度爆炸的问题。这种方法特别适用于激活函…...
)
C++第3课——保留小数点、比较运算符、逻辑运算符、布尔类型以及if-else分支语句(含视频讲解)
文章目录 1、课程笔记2、课程视频 1、课程笔记 #include<iostream>//头文件 input output #include<cmath> //sqrt()所需的头文件 #include<iomanip>//setprecision(1)保留小数点位数所需的头文件 using namespace std; int main(){/*复习上节课内容1、…...

韩媒专访CertiK首席商务官:持续关注韩国市场,致力于解决Web3安全及合规问题
作为Web3.0头部安全公司,CertiK在KBW期间联合CertiK Ventures举办的活动引起了业界的广泛关注。CertiK一直以来与韩国地方政府保持着紧密合作关系,在合规领域提供强有力的支持。而近期重磅升级的CertiK Ventures可以更好地支持韩国本地的区块链项目。上述…...

计算机毕业设计之:宠物服务APP的设计与实现(源码+文档+讲解)
博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ等平台…...
小柴冲刺软考中级嵌入式系统设计师系列二、嵌入式系统硬件基础知识(3)嵌入式系统的存储体系
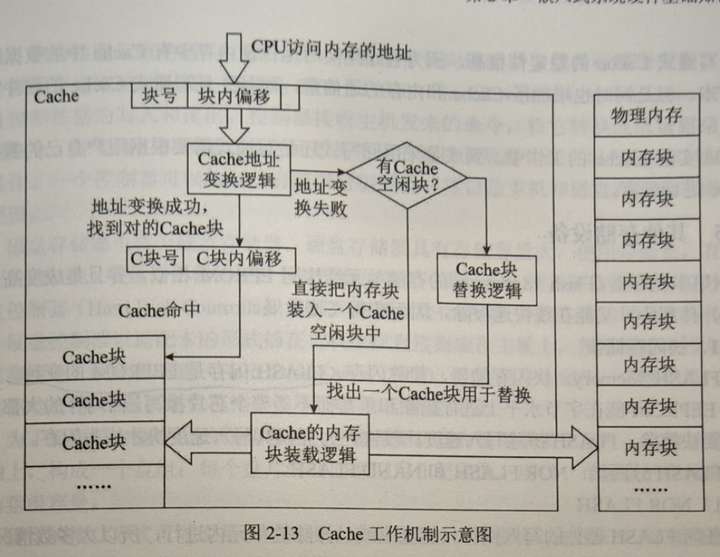
目录 感悟 一、存储系统的层次结构 存储器系统 二、内存管理单元 三、RAM和ROM的种类与选型 1、RAM RAM分类 2、ROM ROM分类 四、高速缓存Cache 五、其他存储设备 flechazohttps://www.zhihu.com/people/jiu_sheng 小柴冲刺软考中级嵌入式系统设计师系列总目录https…...

Unity android 接USBCamera
目录 一、前提 1. unity打包android后,链接USB摄像头,需要USB权限。 二、流程 1.Unity导出android工程,Player配置如图: 2.导出android工程 3.在android工程中找到AndroidManifest.xml加入usb权限相关 <?xml version&quo…...
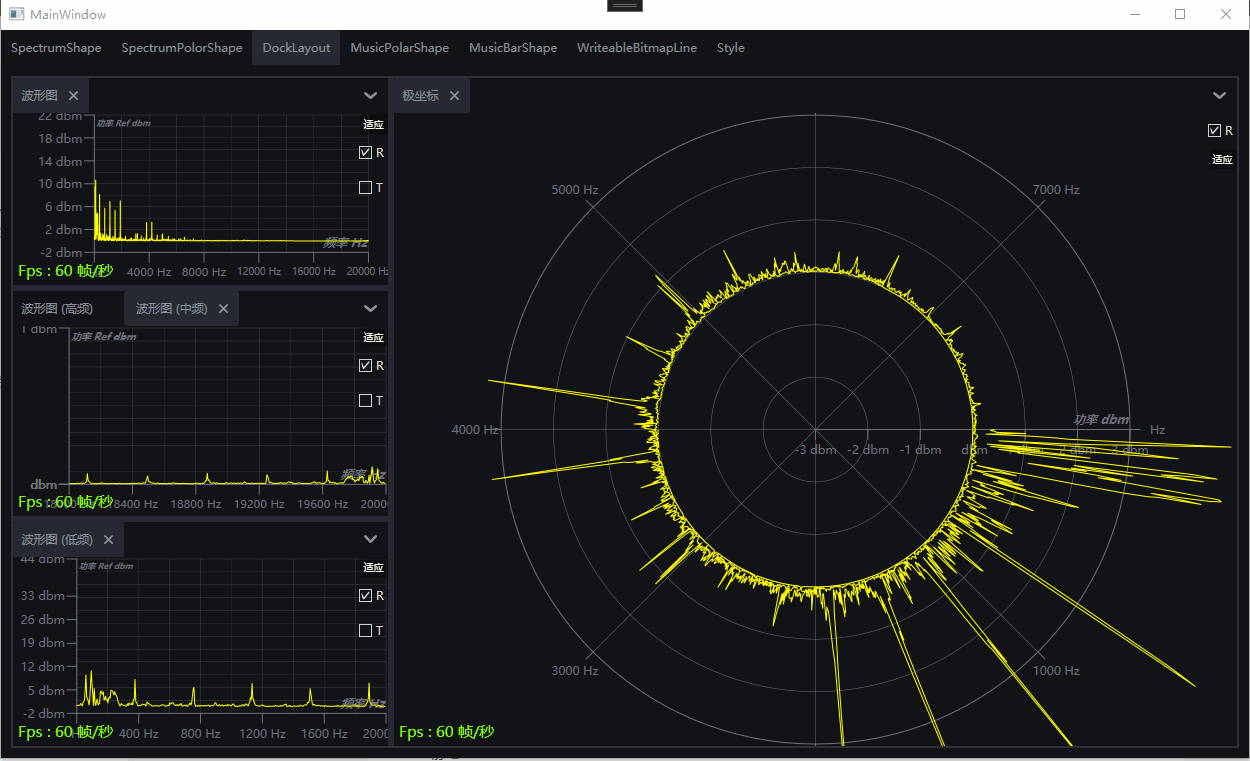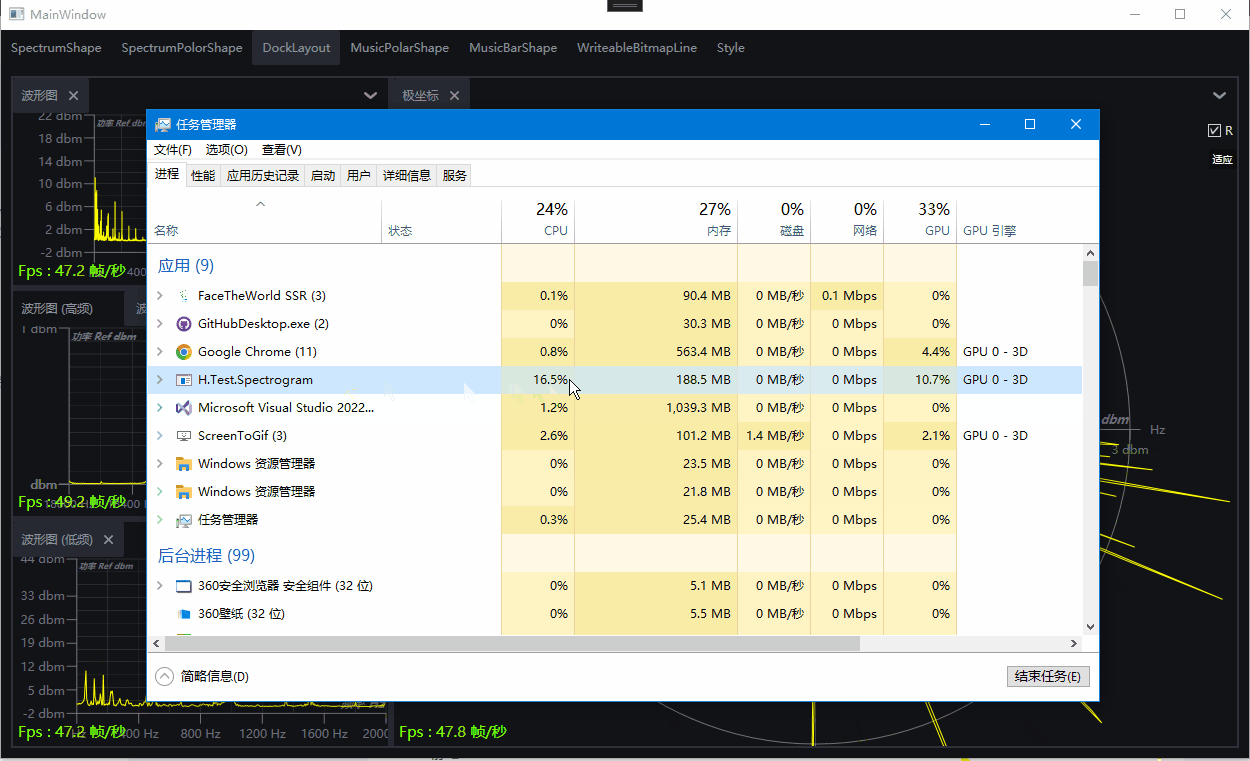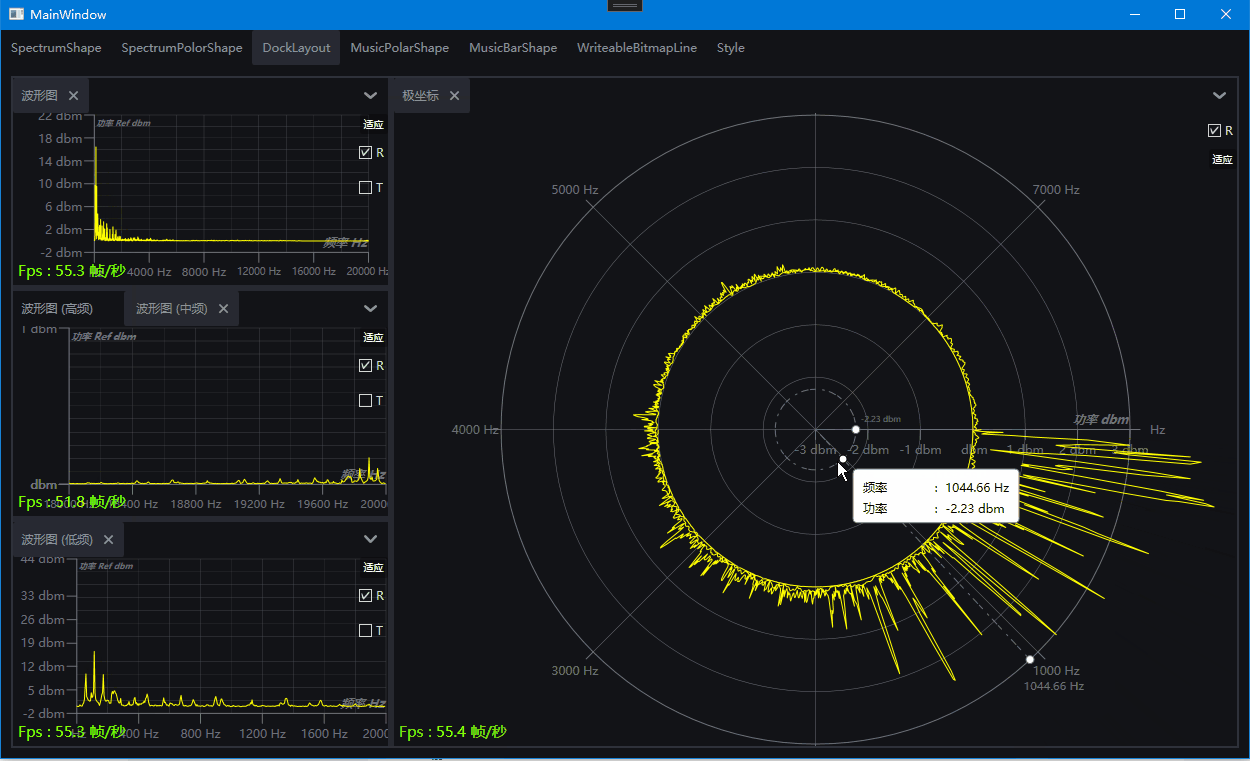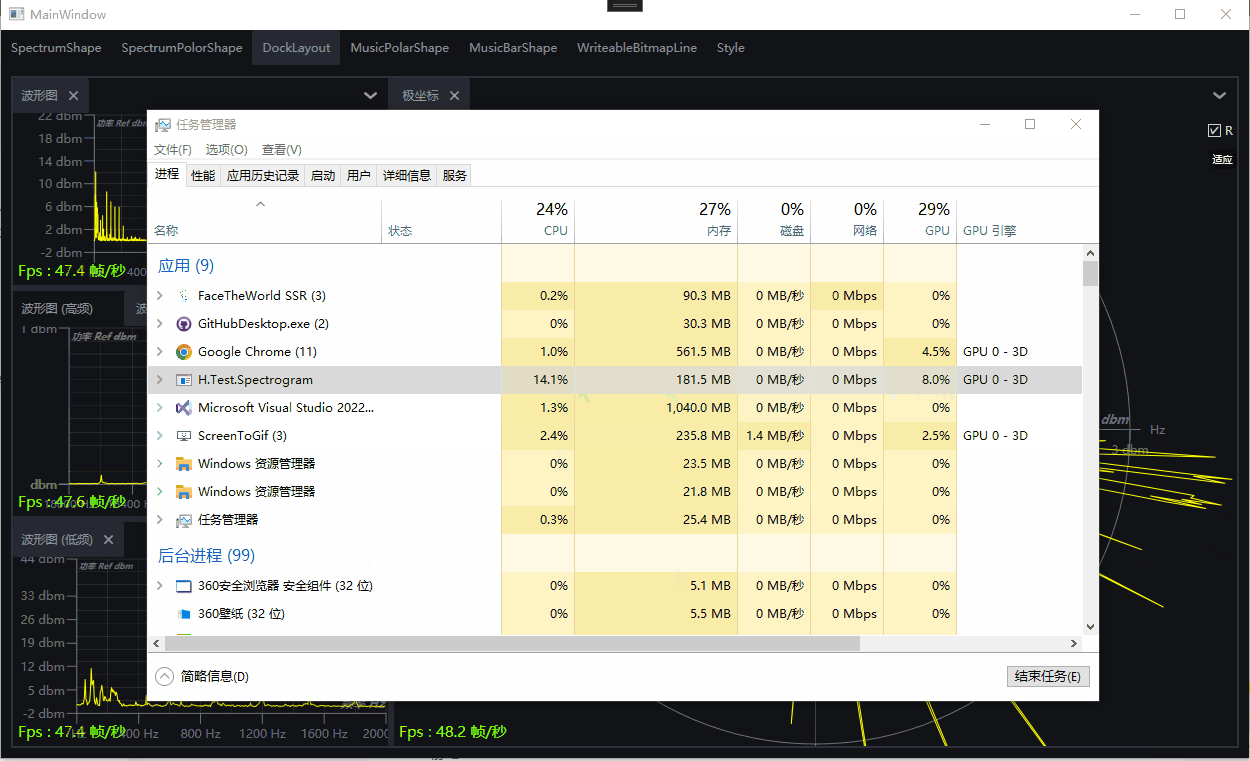
演示:基于WPF的DrawingVisual开发的频谱图和律动图
一、目的:基于WPF的DrawingVisual开发的频谱图和律动图 二、效果演示 波形图 极坐标 律动图极坐标图 律动图柱状图 Dock布局组合效果 三、环境 VS2022,Net7,Win10,NVIDIA RTX A2000 四、主要功能 支持设置起始频率,终止频率,中心…...

【数据结构初阶】排序算法(中)快速排序专题
文章目录 1. 快排主框架2. 快排的不同实现2. 1 hoare版本2. 2 挖坑法2. 3 lomuto前后指针法2. 4 快排的非递归版本 3. 快排优化3. 1 快排性能的关键点分析:3. 1 三路划分3. 2 introsort自省排序 1. 快排主框架 快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。 其…...

Redis缓存双写一致性笔记(上)
Redis缓存双写一致性是指在将数据同时写入缓存(如Redis)和数据库(如MySQL)时,确保两者中的数据保持一致性。在分布式系统中,缓存通常用于提高数据读取的速度和减轻数据库的压力。然而,当数据更新…...

PCB基础
一、简介 PCB:printed circuit board,印刷电路板 主要作用:传输信号、物理支撑、提供电源、散热 二、分类 2.1 按基材分类 陶瓷基板:包括氧化铝、氮化铝、碳化硅基板等,具有优异的导热性,适用于高温和高…...

PostgreSQL 17:新特性与性能优化深度解析
目录 引言核心新特性 块级别增量备份与恢复逻辑复制槽同步参数SQL/JSON的JSON_TABLE命令PL/pgSQL支持数组%TYPE和%ROWTYPE 性能优化 IO合并读取性能参数真空处理过程的内存管理改进写前日志(WAL)锁的改进 升级建议结语 引言 PostgreSQL 17版本于2024年…...
[Linux#58][HTTP] 自己构建服务器 | 实现网页分离 | 设计思路
目录 一. 最简单的HTTP服务器 二.服务器 2.0 Protocol.hpp httpServer.hpp 子进程的创建和退出 子进程退出的意义 父进程关闭连接套接字 httpServer.cc argc (argument count) argv (argument vector) 三.服务器和网页分离 思考与补充: 一. 最简单的HTT…...

7.MySQL内置函数
目录 日期函数时间函数字符串函数数学函数其他函数 日期函数 函数名称描述current_date()当前日期current_time()当前时间current_timesamp()当前时间戳date(datetime)返回datetime参数的日期部分date_add(date, interval d_value_tyep)在date中添加日期函数或时间。interval后…...

如何快速自定义一个Spring Boot Starter!!
目录 引言: 一. 我们先创建一个starter模块 二. 创建一个自动配置类 三. 测试启动 引言: 在我们项目中,可能经常用到别人的第三方依赖,又是引入依赖,又要自定义配置,非常繁琐,当我们另一个项…...
)
【音视频】ffmpeg其他常用过滤器filter实现(6-4)
最近一直在研究ffmpeg的过滤器使用,发现挺有意思的,这里列举几个个人感觉比较有用的过滤器filter,如下是代码实现,同样适用于命令行操作: 1、视频模糊:通过boxblur可以将画面进行模糊处理,第1个…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...
