class 023 随机快速排序
这篇文章是看了“左程云”老师在b站上的讲解之后写的, 自己感觉已经能理解了, 所以就将整个过程写下来了。
这个是“左程云”老师个人空间的b站的链接, 数据结构与算法讲的很好很好, 希望大家可以多多支持左程云老师, 真心推荐.
https://space.bilibili.com/8888480?spm_id_from=333.999.0.0

1. 快速排序过程详解
1.1 逻辑解释
- 先设置一个数组
arr[] = [ ], 下标是:0 ~ (n - 1), - 然后
0 ~ (n - 1)位置随机选择一个数字:p, - 那么就按
p为分界线, 将<= p的数字放在左边, 将> p的数字放在右边, - 然后将
p这个数字放在左边范围的最右侧位置, (当然可能有很多个p, 但是我们不关心, 只是放一个) - 此时这个
p数字算是排好序了. 在整个数组位置上就已经不用变了. - 然后从这个已经排好序的数字
p的左边和右边位置调用递归过程排序就行了. (就是重复上面的过程), 每次都能将一个数字排好序.
1.2 代码实例
这个过程和上面的逻辑实现是一样的, 直接看就能看懂, 这里我就直接说明几个需要注意的点.
l >= r:若是l == r说明只有一个数字, 不用排序, 若是l > r说明数组不存在.Math.random()方法的使用:这个Math.random()方法返回[0, 1)之间任意的一个浮点数, 我感觉说到这里已经能说明问题了, 这个应该是谁都要掌握的, 要是不知道, 就直接随便看一下讲解就行了. 真没有什么好讲的.
public static int[] sortArray(int[] nums) { if (nums.length > 1) { quickSort1(nums, 0, nums.length - 1); } return nums;
} // 随机快速排序经典版(不推荐)
public static void quickSort1(int[] arr, int l, int r) { if (l >= r) { return; } // 随机这一下,常数时间比较大 // 但只有这一下随机,才能在概率上把快速排序的时间复杂度收敛到O(n * logn) int x = arr[l + (int) (Math.random() * (r - l + 1))]; int mid = partition1(arr, l, r, x); quickSort1(arr, l, mid - 1); quickSort1(arr, mid + 1, r);
} // 已知arr[l....r]范围上一定有x这个值
// 划分数组 <=x放左边,>x放右边,并且确保划分完成后<=x区域的最后一个数字是x
public static int partition1(int[] arr, int l, int r, int x) { // a : arr[l....a-1]范围是<=x的区域 // xi : 记录在<=x的区域上任何一个x的位置,哪一个都可以 int a = l, xi = 0; for (int i = l; i <= r; i++) { if (arr[i] <= x) { swap(arr, a, i); if (arr[a] == x) { xi = a; } a++; } } swap(arr, xi, a - 1); return a - 1;
} public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp;
}
2. partition 函数详解
这段代码会有两个分支, 就是 <= x 和 > x, 所以最开始, 设置 i 对传递进来的数组范围上进行遍历,
- 若是
i遍历到的数字<= x, 就让arr[a] 和 arr[i]进行互换(这一步是到了i遍历的数字> x的时候进行交换, 为以后做铺垫), 然后将a++, i++. 此时<= x范围的的数字扩大了. - 若是
i遍历到的数字> x, 就让a不变, i++, - 通过上述过程,
i遍历完数组的数字之后, 可以实现将所有<= x的数字放在数组的左侧, 将所有> x的数字放在数组的右侧. - 然后将
x数字归位到a - 1位置. 因为这样才能保证x数字在数组中已经是排好序了. - 最后返回
a - 1下标.
其中的 a, xi 变量, 左程云老师都在代码的注释中说明好了, 就不画蛇添足了.
// 已知arr[l....r]范围上一定有x这个值
// 划分数组 <=x放左边,>x放右边,并且确保划分完成后<=x区域的最后一个数字是x
public static int partition1(int[] arr, int l, int r, int x) { // a : arr[l....a-1]范围是<=x的区域 // xi : 记录在<=x的区域上任何一个x的位置,哪一个都可以 int a = l, xi = 0; for (int i = l; i <= r; i++) { if (arr[i] <= x) { swap(arr, a, i); if (arr[a] == x) { xi = a; } a++; } } swap(arr, xi, a - 1); return a - 1;
}
3. Partition 函数优化
3.1 优化逻辑
在经典的 Partition 函数中, 只是将所有的位置分成了两个区域, 一次只能是调整好一个数字, 但是有可能在一个数组中, 可能有很多个相同的数字, 比如在随机选择之后, 我们选择了 x, 但是这个 x 在这个数组中, 有很多个, 那我们干脆可以将所有与 x 相等的数字都排好序, 所以对应的:可以将这个数组分为三个区域:左边是 < x 的区域, 中间是 == x 的区域, 右边是 > x 的区域, 这样就有可能一次将数组中的多个数字排好序.
3.2 代码实例
讲解:我们随机选择的一个数字:x, 还是和原来一样, 设置一个 i 遍历数组中的所有数字, 将传进来的数组的最左边设置为 l, 最右边设置为:r, 分为三种情况.
- 若是
< x, 则交换a 和 i, 然后将a++, i++. - 若是
== x, 则只是i++. - 若是
> x, 则交换b 和 i, 然后将b--, i 不变. - 按照上述步骤, 可以将数组分为三个部分.
这个的时间复杂度为:O(n), 因为只是用 i 遍历了整个数组.
需要注意的是:这个函数是有返回值的, 只是用全局变量进行等效果的替换了. 使用的方式和意义及其注意点左程云老师都在注释里说明白了.
// 随机快速排序改进版(推荐)
public static void quickSort2(int[] arr, int l, int r) { if (l >= r) { return; } // 随机这一下,常数时间比较大 // 但只有这一下随机,才能在概率上把快速排序的时间复杂度收敛到O(n * logn) int x = arr[l + (int) (Math.random() * (r - l + 1))]; partition2(arr, l, r, x); // 为了防止底层的递归过程覆盖全局变量 // 这里用临时变量记录first、last int left = first; int right = last; quickSort2(arr, l, left - 1); quickSort2(arr, right + 1, r);
} // 荷兰国旗问题
public static int first, last; // 已知arr[l....r]范围上一定有x这个值
// 划分数组 <x放左边,==x放中间,>x放右边
// 把全局变量first, last,更新成==x区域的左右边界
public static void partition2(int[] arr, int l, int r, int x) { first = l; last = r; int i = l; while (i <= last) { if (arr[i] == x) { i++; } else if (arr[i] < x) { swap(arr, first++, i++); } else { swap(arr, i, last--); } }
}
4. 时间复杂度分析

这个随机行为的时间复杂度需要用期望来估计, 这个已经在前面的时间复杂度章节中说明过了.
4.1 最差情况
最慢的情况是:arr[] = [1, 2, 3, 4, 5, 6, 7], 若是选择了一个最右侧的数字 7, 那就要将左边所有的数字遍历一遍, 将 7 放到正确位置之后, 选择 6, 继续进行遍历, 最后都排好序了, 这个的时间复杂度是:O(n^2).
空间复杂度是:O(n), 因为按照最差情况, 递归过程压的层数是 n 层.
4.2 最优情况
最优情况是随机选择之后的数字在整个数组的最中间位置(按数值大小). 所以递归过程是两个相同的子过程 (近似看成), 然后 Partition 过程的时间复杂度是:O(n), 所以根据 master 公式,
时间复杂度 == 2 * T(N/2) + O(n) == O(n * log(n)).
空间复杂度:因为此时是最优的情况, 所以对应的递归过程也是一个最好的情况, 递归到最底层之后, 返回, 然后进行另一个递归过程, 此时占用的空间是原来最底层的函数使用过的, 是重复利用了的空间, 所以假设数组长度是:n, 所以这个就是一个二分的过程, 空间复杂度:O(log(n)).
当然也有可能是一般情况, 有可能还是比较靠近两侧, 或者是比较靠近中间, 但不是最优情况, 也不是最差情况.
所以根据期望, 最后的时间复杂度是:O(n * log(n)), 空间辅助度是:O(log(n)). 而且这个不是最好情况的时间复杂度和空间复杂度, 这是数学家们根据所有的情况统计之后, 进行严密的论证之后的答案, 是可以和最好的情况相等, 但是不是最好情况直接用的.
注意:这个证明过程很复杂, 不用掌握也不影响后续的学习.
相关文章:

class 023 随机快速排序
这篇文章是看了“左程云”老师在b站上的讲解之后写的, 自己感觉已经能理解了, 所以就将整个过程写下来了。 这个是“左程云”老师个人空间的b站的链接, 数据结构与算法讲的很好很好, 希望大家可以多多支持左程云老师, 真心推荐. https://space.bilibili.com/8888480?spm_id_f…...

如何理解矩阵的复数特征值和特征向量?
实数特征值的直观含义非常好理解,它就是在对应的特征向量方向上的纯拉伸/压缩。 而复数特征值,我们可以把它放在复数域中理解。但是这里给出一个不那么简洁、但是更加直观的理解方式:把它放在实空间中。那么复数特征值表现的就是旋转等比放大…...

怎么查看网站是否被谷歌收录,查看网站是否被搜索引擎收录5个方法与步骤
要查看网站是否被谷歌(Google)或其他搜索引擎收录,是网站管理和SEO(搜索引擎优化)中的一个重要环节。以下是查看网站是否被搜索引擎收录5个方法与步骤,帮助您确认网站是否被搜索引擎成功索引: …...

Java工具--stream流
Java工具--stream流 过滤(filter)统计求最大最小和均值求和(sum)过滤后,对数据进行统计 遍历(map)规约(reduce)排序(sorted)去重(dist…...
什么是 JWT?它是如何工作的?
松哥最近辅导了几个小伙伴秋招,有小伙伴在面小红书时遇到这个问题,这个问题想回答全面还是有些挑战,松哥结合之前的一篇旧文和大伙一起来聊聊。 一 无状态登录 1.1 什么是有状态 有状态服务,即服务端需要记录每次会话的客户端信…...

微信小程序使用picker,数组怎么设置默认值
默认先显示请选择XXX。然后点击弹出选择列表。如果默认value是0的话,他就直接默认显示数组的第一个了。<picker mode"selector" :value"planIndex" :range"planStatus" range-key"label" change"bindPlanChange&qu…...

Springboot生成树工具类,可通过 id/code 编码生成 2.0版本
优化工具类中,查询父级时便利多次的问题 import org.apache.commons.collections4.CollectionUtils; import org.apache.commons.lang3.mutable.MutableLong; import org.springframework.lang.NonNull; import org.springframework.lang.Nullable; import org.spri…...

17、CPU缓存架构详解高性能内存队列Disruptor实战
1.CPU缓存架构详解 1.1 CPU高速缓存概念 CPU缓存即高速缓冲存储器,是位于CPU与主内存间的一种容量较小但速度很高的存储器。CPU高速缓存可以分为一级缓存,二级缓存,部分高端CPU还具有三级缓存,每一级缓存中所储存的全部数据都是…...

算法训练营打卡Day18
目录 二叉搜索树的最小绝对差二叉搜索树中的众数二叉树的最近公共祖先额外练手题目 题目1、二叉搜索树的最小绝对差 力扣题目链接(opens new window) 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例: 思…...

【leetcode】169.多数元素
boyer-moore算法最简单理解方法: 假设你在投票选人 如果你和候选人(利益)相同,你就会给他投一票(count1),如果不同,你就会踩他一下(count-1)当候选人票数为0&…...

MyBatis<foreach>标签的用法与实践
foreach标签简介 实践 demo1 简单的一个批量更新,这里传入了一个List类型的集合作为参数,拼接到 in 的后面 ,来实现一个简单的批量更新 <update id"updateVislxble" parameterType"java.util.List">update model…...

R语言Shiny包新手教程
R语言Shiny包新手教程 1. 简介 Shiny 是一个 R 包,用于创建交互式网页应用。它非常适合展示数据分析结果和可视化效果。 2. 环境准备 安装R和RStudio 确保你的计算机上安装了 R 和 RStudio。你可以从 CRAN 下载 R,或从 RStudio 官网 下载 RStudio。…...

[大象快讯]:PostgreSQL 17 重磅发布!
家人们,数据库界的大新闻来了!📣 PostgreSQL 17 正式发布,全球开发者社区的心血结晶,带来了一系列令人兴奋的新特性和性能提升。 发版通告全文如下 PostgreSQL 全球开发小组今天(2024-09-26)宣布…...

CHI trans--Home节点发起的操作
总目录: CHI协议简读汇总-CSDN博客https://blog.csdn.net/zhangshangjie1/article/details/131877216 Home节点能够发起的操作,包含如下几类: Home to Subordinate Read transactionsHome to Subordinate Write transactionsHome to Subor…...

Rust和Go谁会更胜一筹
在国内,我认为Go语言会成为未来的主流,因为国内程序员号称码农,比较适合搬砖,而Rust对心智要求太高了,不适合搬砖。 就个人经验来看,Go语言简单,下限低,没有什么心智成本,…...

记HttpURLConnection下载图片
目录 一、示例代码1 二、示例代码2 一、示例代码1 import java.io.*; import java.net.HttpURLConnection; import java.net.URL;public class Test {/*** 下载图片*/public void getNetImg() {InputStream inStream null;FileOutputStream fOutStream null;try {// URL 统…...
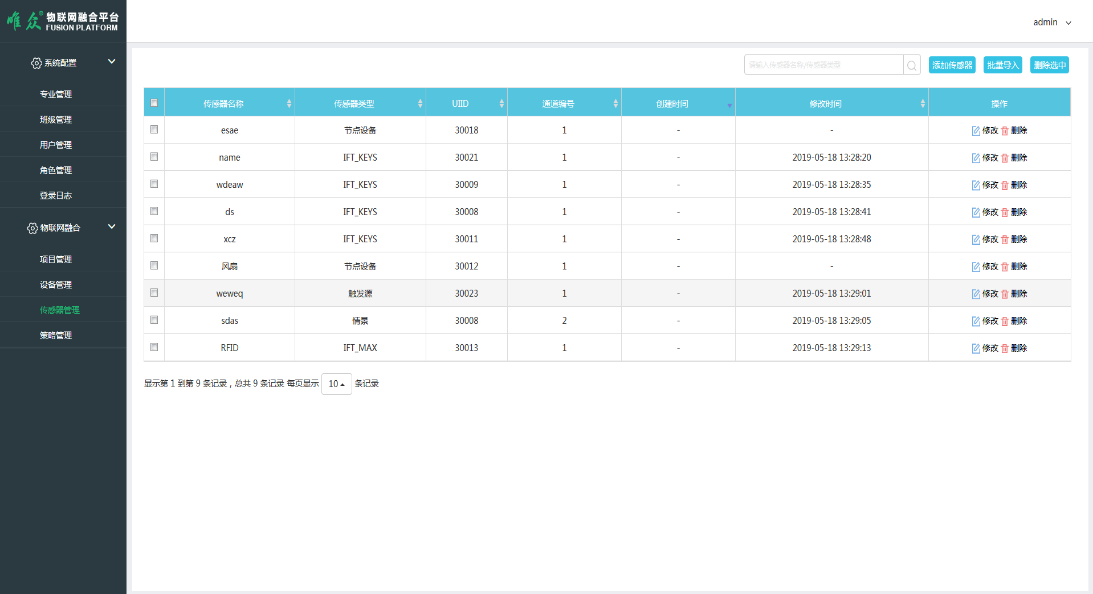
物联网实训室建设的必要性
物联网实训室建设的必要性 一、物联网发展的背景 物联网(IoT)是指通过信息传感设备,按照约定的协议,将任何物品与互联网连接起来,进行信息交换和通信,以实现智能化识别、定位、跟踪、监控和管理的一种网络…...

初识C语言(四)
目录 前言 十一、常见关键字(补充) (1)register —寄存器 (2)typedef类型重命名 (3)static静态的 1、修饰局部变量 2、修饰全局变量 3、修饰函数 十二、#define定义常量和宏…...
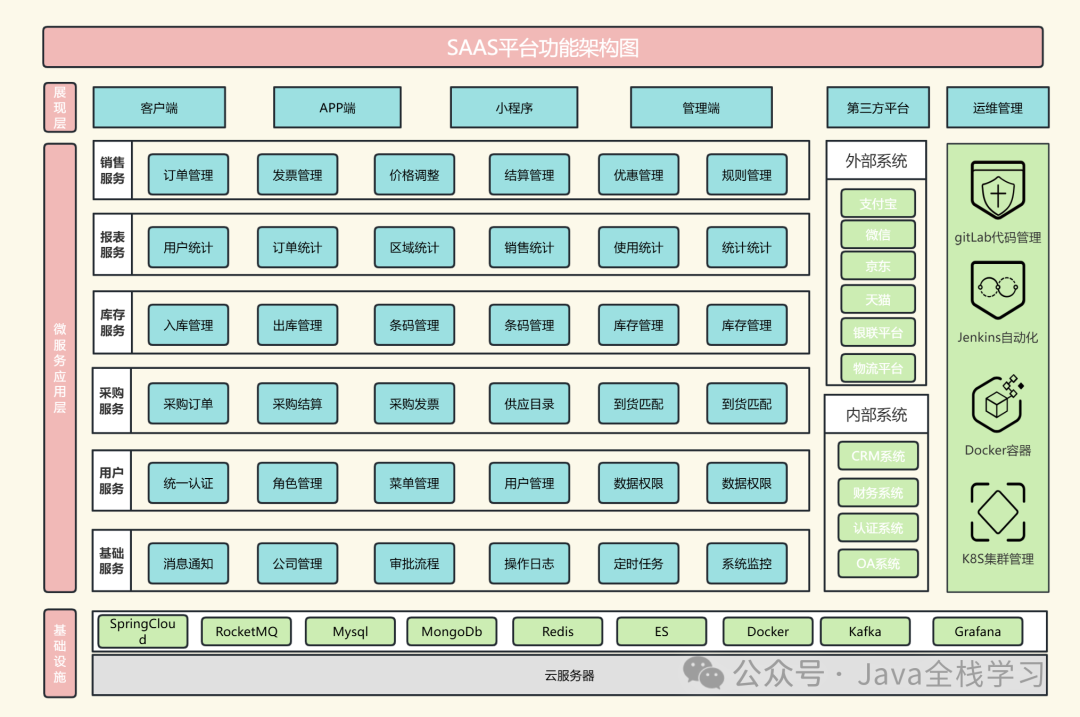
产品架构图:从概念到实践
在当今快速发展的科技时代,产品架构图已成为产品经理和设计师不可或缺的工具。它不仅帮助我们理解复杂的产品体系,还能指导我们进行有效的产品设计和开发。本文将深入探讨产品架构图的概念、重要性以及绘制方法。 整个内容框架分为三个部分,…...

smartctl 命令:查看硬盘健康状态
一、命令简介 smartctl 命令用于获取硬盘的 SMART 信息。 介绍硬盘SMART 硬盘的 SMART (Self-Monitoring, Analysis, and Reporting Technology) 技术用于监控硬盘的健康状态,并能提供一些潜在故障的预警信息。通过查看 SMART 数据,用户可以了解硬…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
