P3131 [USACO16JAN] Subsequences Summing to Sevens S Python题解
[USACO16JAN] Subsequences Summing to Sevens S
题目描述
Farmer John’s N N N cows are standing in a row, as they have a tendency to do from time to time. Each cow is labeled with a distinct integer ID number so FJ can tell them apart. FJ would like to take a photo of a contiguous group of cows but, due to a traumatic childhood incident involving the numbers 1 … 6 1 \ldots 6 1…6, he only wants to take a picture of a group of cows if their IDs add up to a multiple of 7.
Please help FJ determine the size of the largest group he can photograph.
给你n个数,分别是a[1],a[2],…,a[n]。求一个最长的区间[x,y],使得区间中的数(a[x],a[x+1],a[x+2],…,a[y-1],a[y])的和能被7整除。输出区间长度。若没有符合要求的区间,输出0。
输入格式
The first line of input contains N N N ( 1 ≤ N ≤ 50 , 000 1 \leq N \leq 50,000 1≤N≤50,000). The next N N N
lines each contain the N N N integer IDs of the cows (all are in the range
0 … 1 , 000 , 000 0 \ldots 1,000,000 0…1,000,000).
输出格式
Please output the number of cows in the largest consecutive group whose IDs sum
to a multiple of 7. If no such group exists, output 0.
样例 #1
样例输入 #1
7
3
5
1
6
2
14
10
样例输出 #1
5
提示
In this example, 5+1+6+2+14 = 28.
题解
准备国庆假期了,脑子也变得不太好使,这种题我居然没有第一时间想到答案,非常难受。因为脑子进水了,所以我看了别人C++的题解,看到:
( A − B ) m o d n u m ≡ 0 (A-B) \bmod num \equiv 0 (A−B)modnum≡0
等价于
A ≡ B m o d n u m A\equiv B \bmod num A≡Bmodnum
唉,这个同余定理这么常用,为什么我时不时就把它给忘记呢?
大家可以去参考一下大佬的题解:题解 P3131 【[USACO16JAN]子共七Subsequences Summing to Sevens】
这里给出对应的Python代码:
def Solution2():N = int(input())Prefix = 0yvshu = {i: [] for i in range(7)}for i in range(N):Prefix += int(input())yvshu[Prefix%7].append(i+1)ans = max(yvshu[0]) if yvshu[0] else 0for key in yvshu.keys():if len(yvshu[key]) > 1:ans = max(ans, yvshu[key][-1] - yvshu[key][0])print(ans)Solution2()

关于上面那个定理的题我还可以提供一题:
Ringo’s Favorite Numbers 2
相关文章:

P3131 [USACO16JAN] Subsequences Summing to Sevens S Python题解
[USACO16JAN] Subsequences Summing to Sevens S 题目描述 Farmer John’s N N N cows are standing in a row, as they have a tendency to do from time to time. Each cow is labeled with a distinct integer ID number so FJ can tell them apart. FJ would like to ta…...

鸿蒙NEXT开发-ArkUI(基于最新api12稳定版)
注意:博主有个鸿蒙专栏,里面从上到下有关于鸿蒙next的教学文档,大家感兴趣可以学习下 如果大家觉得博主文章写的好的话,可以点下关注,博主会一直更新鸿蒙next相关知识 专栏地址: https://blog.csdn.net/qq_56760790/…...

Matplotlib 使用 LaTeX 渲染图表中的文本、标题和数学公式
Matplotlib 使用 LaTeX 渲染图表中的文本、标题和数学公式 Matplotlib 是一个功能强大的 Python 库,用于绘制各种高质量的图表和图形。在许多科研和技术文档中,数学公式是不可或缺的一部分,LaTeX 提供了精美的数学公式渲染能力。Matplotlib …...

Android 安卓内存安全漏洞数量大幅下降的原因
谷歌决定使用内存安全的编程语言 Rust 向 Android 代码库中写入新代码,尽管旧代码(用 C/C 编写)没有被重写,但内存安全漏洞却大幅减少。 Android 代码库中每年发现的内存安全漏洞数量(来源:谷歌)…...

c++primier第十二章类和动态内存
本章内容包括: 对类成员使用动态内存分配隐式和显式地复制构造函数隐式和显式地重载赋值操作符在构造函数中使用new所必须完成的工作使用静态类成员 将布局new操作符用于对象使用指向对象的指针实现队列抽象数据类型(ADT) 动态内存和类 复习范例和静态类成员 首…...

Ansible学习之ansible-pull命令
想要知道ansible-pull是用来做什么的,就需要了解Ansible的工作模,Ansible的工作模式有两种: push模式 push推送,这是Ansible的默认模式,在主控机上编排好playbook文件,push到远程主机上来执行。pull模式 p…...

Linux:磁盘管理
一、静态分区管理 静态的分区方法不可以动态的增加或减少分区的容量。 1、磁盘分区-fdisk 该命令是用于查看磁盘分区情况,和分区管理的命令 命令格式:fdisk [选项] 设备文件名常用命令: -h:查看分区信息 fdisk系统常用命令&…...

FP7209: 用于紫外线消毒灯的 升压LED恒流驱动芯片
现在社会对于居家消毒也越发重视起来。而居家消毒除了75%浓度酒精及各类消毒液外,利用紫外线灯给衣物表面、房间消毒也是一种很好的选择。FP7209 定位于低压线性恒流驱动,精度高、外围电路简单、使用方便且可靠性高,更可广泛应用于商业照明系…...

【华为HCIP实战课程二】OSPF基础介绍和OSPF RID NBMA配置详解
一、OSPF多区域 自治系统(Autonomous System) 一个自治系统是指使用同一种路由协议交换路由信息的一组路由器 1、Area0为骨干区域 2、ABR--关乎3类LSA后续详解 ABR用来连接骨干区域Area0和非骨干区域,它与骨干区域之间既可以是物理连接,也可以是逻辑上的连接。 3、AS…...
——单例模式)
网络编程(13)——单例模式
十三、day13 今天学习如何单例模式实现逻辑层的设计。内容包括服务器如何能捕获信号使其安全退出、单例模标类 1. 什么是单例模式? 单例模式(Singleton),保证一个类仅有一个实例,并提供一个访问它的全局访问点&…...

基于定制开发与2+1链动模式的商城小程序搭建策略
摘要:本文探讨商城小程序的搭建策略,对比自主组建团队和第三方开发两种方式,强调以第三方开发模式为主的优势。阐述在第三方开发模式下,结合定制开发和21链动模式,如何搭建一款有助于企业商业模式创新与智能商业升级的…...

银河麒麟,apt 安装软件报错640Unknown Status
今天把银行麒麟的机器恢复出厂了,然后apt install 安装极其不稳定,故障现象如下图所示: 错误提示里面有: 640 Unknown Status [IP: 106.116.184.122 80] E: 无法下载 http://archive.kylinos.cn/kylin/KYLIN-ALL/pool/universe/f…...

python UNIT 3 选择与循环(2)
目录 1。循环的优化 经典优化分析: 未优化的代码: 细节分析: 优化后的代码: 优化的细节: 性能对比 优化的关键在于: 经典习题讲解:(紫色的解析请重点关注一下) 1。例三 个人代码解析…...

828华为云征文|部署在线文档应用程序 CodeX Docs
828华为云征文|部署在线文档应用程序 CodeX Docs 一、Flexus云服务器X实例介绍二、Flexus云服务器X实例配置2.1 重置密码2.2 服务器连接2.3 安全组配置2.4 Docker 环境搭建 三、Flexus云服务器X实例部署 CodeX Docs3.1 CodeX Docs 介绍3.2 CodeX Docs 部署3.3 CodeX…...

Linux的多线程(线程的创建,退出,取消请求,取消处理例程,线程属性的设置)
进程:是系统分配资源的最小单位,系统会为每一个进程分配一块独立的虚拟内存空间 线程:是系统调度的最小单位,系统不会为线程分配新的内存空间,但是线程也参与系统调度 cpu把时间片分给每一个进程,进程中的时间片再切分分给每一个线程,所以线程也会得到…...

git 本地代码关联远程仓库并推送
初始化代码仓库 如果你的本地项目还没有使用Git管理,首先需要在项目根目录下初始化一个Git仓库 git init添加远程仓库地址 使用 git remote add 命令添加远程仓库 git remote add origin https://github.com/username/repository.git获取远程分支信息 使用 git…...
推荐一个可以把PDF样本册转换为翻页电子书的网站
随着互联网的普及,越来越多的企业和个人开始意识到线上展览的重要性。如何将实体样本册转化为线上版本,让更多人了解和欣赏自己的产品与服务? 一、网站简介 这款PDF样本册免费上传网站名为“FLBOOK”,致力于为广大用户提供便捷…...
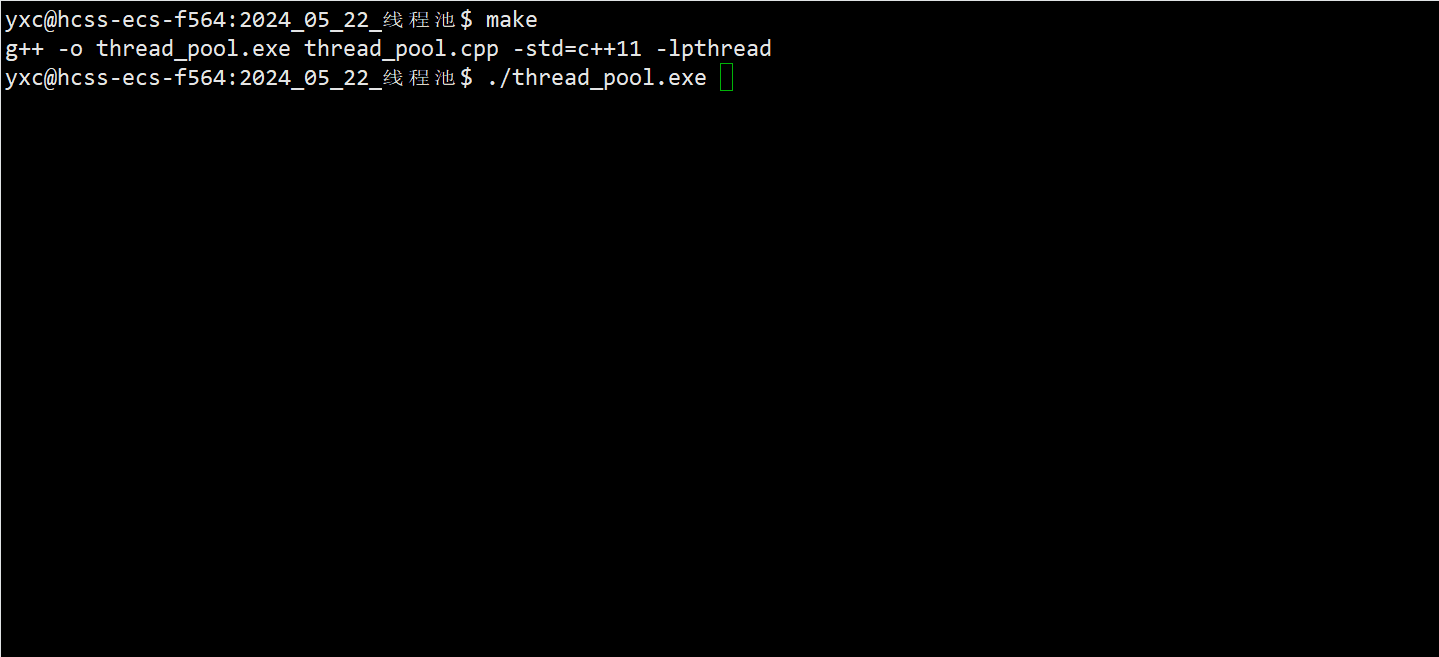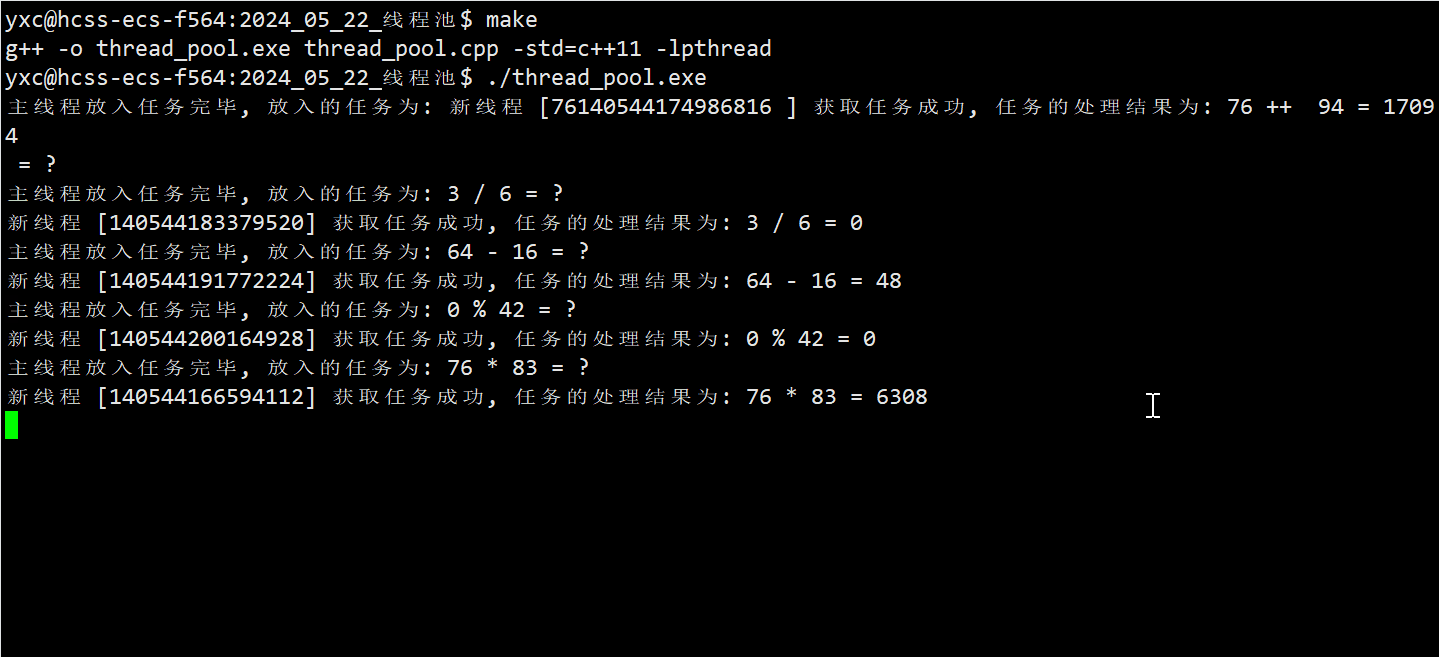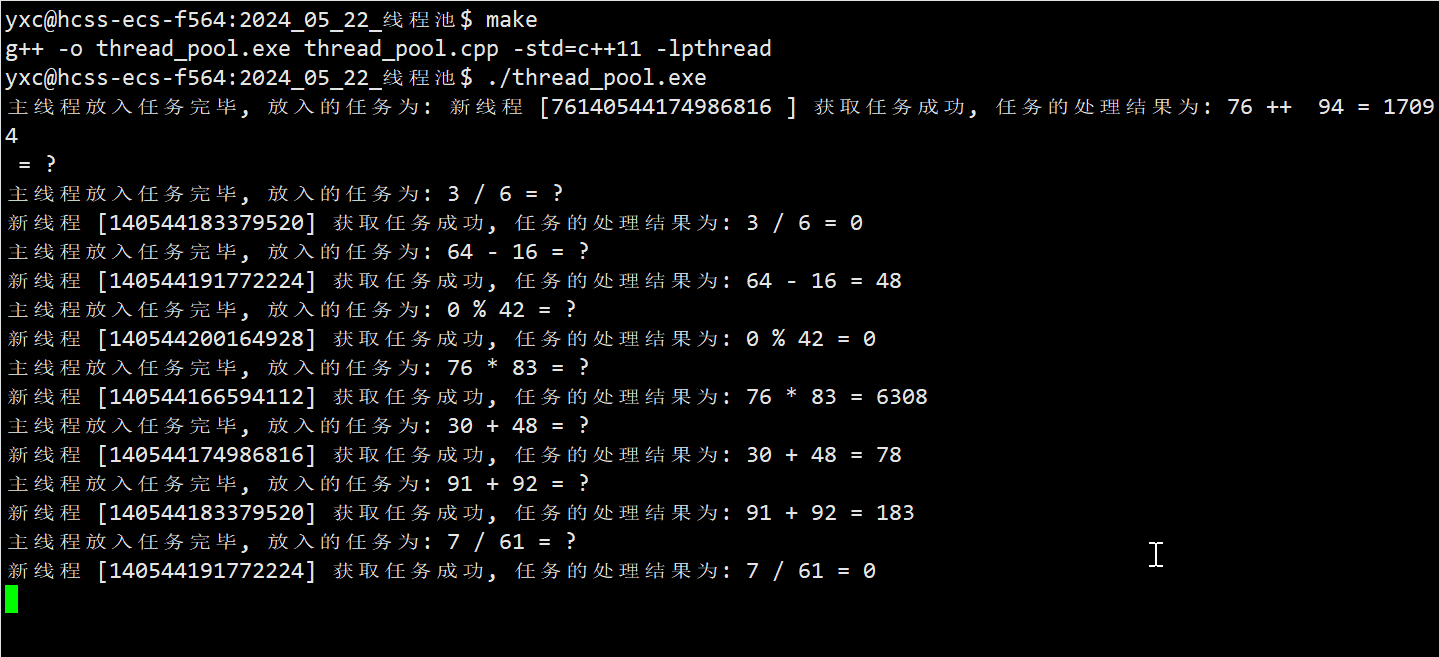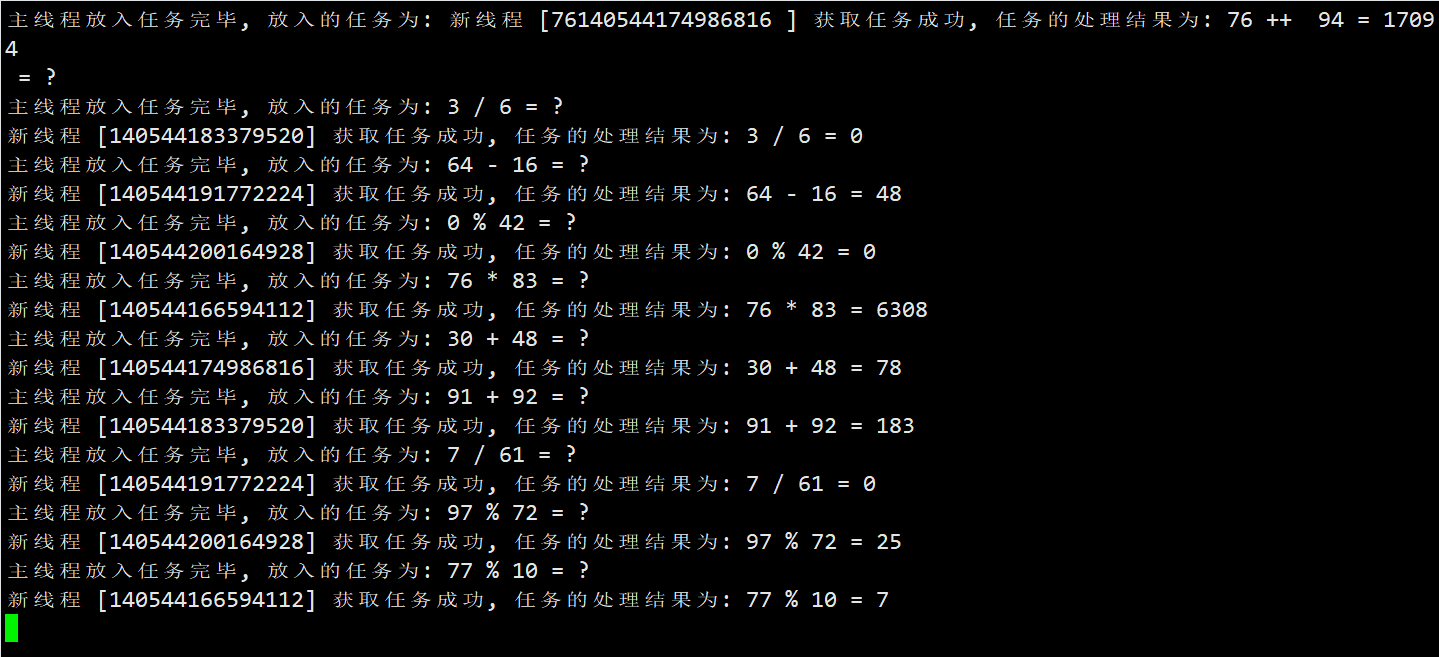
【Linux 23】线程池
文章目录 🌈 一、线程池的概念🌈 二、线程池的应用场景🌈 三、线程池的实现 🌈 一、线程池的概念 线程池 (thread pool) 是一种利用池化技术的线程使用模式。 虽然创建线程的代价比创建进程的要小很多,但小并不意味着…...

Rust SQLite 跨平台使用
引言 Rust因其内存安全性和高性能受到越来越多开发者的青睐。在许多项目中,SQLite作为一种轻量级的嵌入式数据库,与Rust的结合为跨平台应用程序提供了强大的支持。本文将详细探讨Rust如何实现跨平台功能,如何在不同平台上使用Rust库…...

docker运行arm64架构的镜像、不同平台镜像构建
背景 Docker 允许开发者将应用及其依赖打包成一个轻量级、可移植的容器,实现“一次构建,到处运行”的目标。然而,不同的操作系统和硬件架构对容器镜像有不同的要求。例如,Linux 和 Windows 系统有不同的文件系统和系统调用&#…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
