KKT实际运用 -MATLAB
- FMINCON函数可以很方便的求出:
fun:目标函数,即需要最小化的函数,输入参数为向量x,输出为标量f(x)。x0:初始点,即求解过程的起始点,可以是标量、向量或矩阵。A和b:线性不等式约束的系数矩阵和向量,满足A*x <= b。Aeq和beq:线性等式约束的系数矩阵和向量,满足Aeq*x = beq。lb和ub:变量的下界和上界向量,满足lb <= x <= ub。nonlcon:非线性约束函数(可选),定义非线性不等式c(x) <= 0和非线性等式ceq(x) = 0。options:优化选项(可选),用于控制求解过程的参数,如算法选择、容差设置等。
% 项目名称:KKT实际运用
% 更新时间:2024/09/25
% 背景:(Karush-Kuhn-Tucker方法)是一种用于求解约束优化问题的数学方法,该方法的核心思想是通过引入拉格朗日乘子和对偶性理论,将约束优化问题转化为无约束优化问题,从而简化求解过程。
% 作者:月白风清江有声 % 定义目标函数
fun = @(x) 4*x(1) - 3*x(2); % 假设我们要最小化的目标函数 % 初始点
x0 = [0, 0]; % 线性不等式约束 A*x <= b
A = [1, 1; 0, -1];
b = [4; 7]; % 线性等式约束(这里没有,所以留空)
Aeq = [];
beq = []; % 定义非线性不等式约束函数
% 注意:这个函数返回的是非线性不等式的原始表达式值,但fmincon会尝试最小化它
% 对于 -(x1-3)^2 + x2 + 1 >= 0,我们直接返回其表达式值
% 因为fmincon会尝试找到使这些值尽可能小的x,从而满足原不等式
% 定义非线性不等式约束函数
% 直接返回不等式约束的表达式值和空向量
%deal 函数用于同时返回两个值。第一个值是原不等式约束的表达式值,第二个值是一个空向量 [],表示没有非线性等式约束。
nonlincon = @(x) deal((x(1)-3)^2 - x(2) - 1, []);
% 调用fmincon
options = optimoptions('fmincon','Algorithm','sqp'); % 设置算法为SQP
[x, fval] = fmincon(fun, x0, A, b, Aeq, beq, [], [], nonlincon, options);
% 显示结果
disp('最优解 x:');
disp(x);
disp('目标函数值 fval:');
disp(fval);% 第二个优化问题 % 定义目标函数(注意这里使用了三个变量)
fun_bar = @(x_bar) -3*x_bar(1)^2 - x_bar(2)^2 - 2*x_bar(3)^2; % 初始点(现在是三维的)
x0_bar = [1, 1, 1]; % 线性不等式约束 A_bar*x_bar <= b_bar A_bar = [1, -1, 0; -1, 0, 0; 0, -1, 0; 0, 0, -1];
b_bar = [0; 0; 0; 0]; Aeq_bar = [];
beq_bar = []; nonlincon_bar = @(x_bar) deal([], (x_bar(1)^2 + x_bar(2))^2 + x_bar(3)^2 - 3);
% 调用fmincon
options_bar = optimoptions('fmincon','Algorithm','sqp'); % 设置算法为SQP
[x_bar, fval_bar] = fmincon(fun_bar, x0_bar, A_bar, b_bar, Aeq_bar, beq_bar, [], [], nonlincon_bar, options_bar); % 显示结果
disp('第二个优化问题的最优解 x_bar:');
disp(x_bar);
disp('第二个优化问题的目标函数值 fval_bar:');
disp(fval_bar);
相关文章:

KKT实际运用 -MATLAB
FMINCON函数可以很方便的求出:fun:目标函数,即需要最小化的函数,输入参数为向量x,输出为标量f(x)。x0:初始点,即求解过程的起始点,可以是标量、向量或矩阵。A和b:线性不等…...

php在线相册
1、将静态页面效果完成 解压到www里 整个数据 暂时是错误的 建立连接密码为root 运行sql文件 右键根目录刷新 刷新后成功 开始 测试 如果需要上传照片,点击创建相册,选择上传文件,选择文件后退出 导入alumbenew2 2.提交表单方式 3.利用ph…...

Xcode手动安装SDK模拟器
1.下载SDK模拟器&Xcode SDK和Xcode官方下载地址 2.下载好后使用命令将SDK导入到Xcode中如下命令 注:我是在/Applications 目录下执行的命令,模拟其地址直接拖拽过来 sudo xcode-select -s Xcode.app xcodebuild -runFirstLaunch xcodebuild -imp…...
Docker安装consul + go使用consul + consul知识
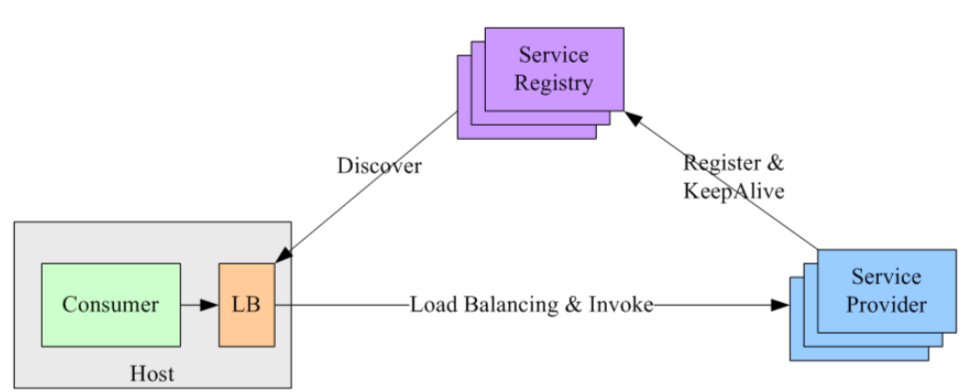
1. 什么是服务注册和发现 假如这个产品已经在线上运行,有一天运营想搞一场促销活动,那么我们相对应的【用户服务】可能就要新开启三个微服务实例来支撑这场促销活动。而与此同时,作为苦逼程序员的你就只有手动去 API gateway 中添加新增的这…...

JWT 漏洞 - 学习手册
0x01:JWT 前导知识 0x0101:JWT 详解 0x02:JWT 漏洞介绍 0x0201:JWT 漏洞介绍 0x03:JWT 挖掘思路 JWT 漏洞挖掘思路 - JWT Payload 敏感信息泄露 备注:通过泄露的 JWT Payload 获取用户的敏感信息&#…...

HTML【知识改变命运】03font 字体标签
题目:在页面上显示"北京"两个字,字体为微软雅黑,颜色为红色,大小为40xp; font标签可以修饰字体的大小,颜色,和字体 属性:color颜色,face字体,size大…...

集师专属知识付费小程序搭建 心理咨询小程序搭建
一、产品简介 集师SaaS知识付费软件,为知识创业者或商家提供一站式内容交付解决方案,助力商家搭建集品牌传播、商业变现和用户运营于一体的线上知识服务系统,覆盖全渠道经营场景,占据每个流量入口,使流量变现快速高效…...

https://www.aitoolpath.com/ 一个工具数据库,目前储存了有2000+各种工具。每日更新
AI 工具爆炸?别怕,这个网站帮你整理好了! 哇塞,兄弟们!AI 时代真的来了!现在各种 AI 工具跟雨后春笋似的,噌噌噌地往外冒。AI 写作、AI 绘画、AI 代码生成……简直是要逆天啊! 可是…...
)
科技的成就(六十三)
583、八小时工作制 最先提出这种理念的人竟然也是一名企业家,而且还是一名空想社会主义者。这名叫做罗伯特欧文的英国人,也凭借先进的人本管理理念成为了现代人事管理之父。 584、SDN(软件定义网络) "SDN(软件定…...

浅谈抗量子密码学:保护未来的数字安全
一、引言 随着量子计算机技术的发展,传统的加密算法面临前所未有的挑战。量子计算机利用量子位(qubits)的特性,能够在理论上比经典计算机更快地破解现有的加密系统。为了应对这一威胁,研究者们正在开发所谓的“抗量子…...

10款物联网开源嵌入式操作系统对比分析
摘要 本文对目前市场上广受欢迎的10款物联网开源嵌入式操作系统进行了深度对比分析,包括Huawei LiteOS、RT-Thread、AliOS Things等。通过探讨这些操作系统的实时性、可扩展性、特点、运行要求、开发社区活跃度和应用领域等方面,帮助开发者更好地理解它…...

Elasticsearch深度攻略:核心概念与实践应用
目录 一、Elasticsearch简介1、Elasticsearch是什么2、Elasticsearch的应用场景3、Elasticsearch的核心概念 二、Elasticsearch安装与配置1、安装Elasticsearch(1)系统要求(2)下载Elasticsearch(3)解压安装…...

TLS详解
什么是TLS TLS(Transport Layer Security)传输层安全性协议 ,它的前身是SSL(Secure Sockets Layer)安全套接层,是一个被应用程序用来在网络中安全的通讯协议, 防止电子邮件、网页、消息以及其他协议被篡改或是窃听。是用来替代SSL的…...

正则表达式中的特殊字符
正则表达式中的特殊字符 字符类预定义字符类量词锚点分组和捕获选择、分支和条件反义和否定转义字符示例 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神的孩子都在歌唱 在正则表达式中,有许…...

EP42 公告详情页
文件路径: E:/homework/uniappv3tswallpaper/api/apis.js 先添加相应的api。 import {request } from "/utils/requset.js"export function apiGetBanner() {return request({url: "/homeBanner"}) } export function apiGetDayRandom() {ret…...

游戏找不到xinput1_3.dll的原因及解决方法
1. xinput1_3.dll 基本信息 1.1 文件名 xinput1_3.dll 是一个动态链接库(DLL)文件,它属于 Microsoft DirectX for Windows 的一部分。这个文件主要负责处理与 Xbox 360 控制器和其他兼容 XInput 标准的游戏手柄相关的输入信号,确…...

防反接电路设计
方案1 串联二极管, 优点:成本低、设计简单 缺点:损耗大,P ui 方案2 串联自恢复保险丝 当电源反接的时候,D4导通,F2超过跳闸带你留,就会断开,从而保护了后级电路 方案3 H桥电路…...

SpringMVC源码-AbstractHandlerMethodMapping处理器映射器将@Controller修饰类方法存储到处理器映射器
SpringMVC九大内置组件之HandlerMapping处理器映射器-AbstractHandlerMethodMapping类以及子类RequestMappingHandlerMapping如何将Controller修饰的注解类以及类下被注解RequestMapping修饰的方法存储到处理器映射器中。 从RequestMappingHandlerMapping寻找: AbstractHandle…...

毕业设计选题:基于ssm+vue+uniapp的购物系统小程序
开发语言:Java框架:ssmuniappJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:M…...
】力扣583. 两个字符串的删除操作)
【动态规划-最长公共子序列(LCS)】力扣583. 两个字符串的删除操作
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 “sea”, word2 “eat” 输出: 2 解释: 第一步将 “sea” 变为 “ea” ,第二步将 "e…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
