单片机的原理及应用
单片机的原理及应用
1. 单片机的基本原理
1.1. 组成部分
单片机主要由以下几个部分组成:
中央处理器(CPU):执行指令并控制整个系统的操作。
存储器:
程序存储器(Flash):存储用户程序代码,通常是非易失性存储器。
数据存储器(RAM):存储运行时数据,通常是易失性存储器。
输入输出端口(I/O):与外部设备(传感器、执行器等)进行数据交互。
定时器/计数器:用于计时、事件计数等功能。
串行通信接口:支持数据传输的接口,如 UART、SPI、I2C 等。
1.2. 工作原理
单片机的工作原理可以简单描述为:
程序加载:用户程序代码被加载到程序存储器中。
指令执行:CPU 从程序存储器中逐条读取并执行指令。执行过程涉及算术运算、数据传输、逻辑判断等操作。
外设交互:通过输入输出端口与外部设备交互,处理来自传感器的数据或控制执行器。
反馈控制:根据输入数据和处理结果,执行特定的控制操作,完成预定的任务。
2. 单片机的应用领域
单片机因其小巧、低功耗和高集成度,被广泛应用于以下领域:
2.1. 工业控制
自动化设备:用于控制电机、传感器、执行器等设备,实现生产线的自动化。
数据采集系统:监测温度、压力、流量等工业参数并进行数据处理。
2.2. 家庭自动化
智能家居:控制家电(如灯光、空调、门锁等),实现智能化管理。
安全系统:实现防盗报警、监控等功能。
2.3. 交通管理
智能交通信号灯:根据实时交通流量调整信号灯的工作状态。
汽车电子:控制汽车的各个电子系统,如发动机控制单元(ECU)、空调等。
2.4. 消费电子
家用电器:微波炉、洗衣机、冰箱等家用电器的控制系统。
可穿戴设备:健康监测、运动追踪等功能的实现。
2.5. 医疗设备
医疗监护仪:实时监测患者的生理参数(如心率、血压等)。
智能药箱:提醒患者按时服药并记录用药情况。
3. 单片机的开发与编程
3.1. 硬件开发
开发板:使用单片机开发板(如 Arduino、STM32、PIC 等)进行原型设计和测试。
外设连接:通过电路图和原理图连接传感器、显示器、执行器等外部设备。
3.2. 编程语言
汇编语言:较底层,适合对单片机硬件进行直接控制。
C/C++ 语言:大多数单片机都支持 C 语言编程,便于开发和维护。
专用开发环境:如 Keil、MPLAB、Arduino IDE 等。
3.3. 编程流程
环境搭建:安装编程环境和工具链。
编写程序:使用适当的编程语言编写应用程序。
编译与下载:将程序编译为机器代码并下载到单片机中。
调试与测试:使用调试工具(如 JTAG、SWD)对程序进行调试和测试。
4. 单片机的选型与设计
在选择合适的单片机时,需要考虑以下几个因素:
性能需求:根据应用需求选择合适的处理器速度、存储器和外设接口。
功耗要求:在便携式和电池供电的设备中,低功耗是一个重要的考量因素。
价格:根据预算选择适合的单片机型号。
可编程性:选择支持常用编程语言和开发环境的单片机。
5. 未来发展趋势
智能化与物联网:随着物联网的快速发展,单片机将越来越多地与互联网连接,实现智能家居、智能城市等应用。
集成度提升:未来单片机的集成度将继续提高,可能集成更多的功能,如无线通信模块、传感器等。
开放性与标准化:越来越多的单片机将支持开放标准,促进不同设备之间的互联互通。
相关文章:

单片机的原理及应用
单片机的原理及应用 1. 单片机的基本原理 1.1. 组成部分 单片机主要由以下几个部分组成: 中央处理器(CPU):执行指令并控制整个系统的操作。 存储器: 程序存储器(Flash):存储用户…...

Python数据分析篇--NumPy--入门
我什么也没忘,但是有些事只适合收藏。不能说,也不能想,却又不能忘。 -- 史铁生 《我与地坛》 NumPy相关知识 1. NumPy,全称是 Numerical Python,它是目前 Python 数值计算中最重要的基础模块。 2. NumPy 是针对多…...

OJ在线评测系统 后端 判题机模块预开发 架构分析 使用工厂模式搭建
判题机模块预开发(架构师)(工厂模式) 判题机模块 是为了把代码交个代码沙箱去处理 得到结果返回 代码沙箱 梳理判题模块和代码沙箱的关系 判题模块:调用代码沙箱 把代码和输入交给代码沙箱去执行 代码沙箱:只负责接受代码和输入 返回编译的结果 不负…...

linux 目录文件夹操作
目录 查看文件夹大小: Linux统计文件个数 2.统计文件夹中文件个数ls -l ./|grep "^-"|wc -l 4.统计文件夹下文件个数,包括子文件ls -lR | grep "^-"| wc -l 统计文件个数 移动绝对目录: 移动相对目录 test.py报错…...

(Linux驱动学习 - 4).Linux 下 DHT11 温湿度传感器驱动编写
DHT11的通信协议是单总线协议,可以用之前学习的pinctl和gpio子系统完成某IO引脚上数据的读与写。 一.在设备树下添加dht11的设备结点 1.流程图 2.设备树代码 (1).在设备树的 iomuxc结点下添加 pinctl_dht11 (2).在根…...

前端登录页面验证码
首先,在el-form-item里有两个div,各占一半,左边填验证码,右边生成验证码 <el-form-item prop"code"><div style"display: flex " prop"code"><el-input placeholder"请输入验证…...
【鸿蒙】HarmonyOS NEXT应用开发快速入门教程之布局篇(上)
系列文章目录 【鸿蒙】HarmonyOS NEXT开发快速入门教程之ArkTS语法装饰器(上) 【鸿蒙】HarmonyOS NEXT开发快速入门教程之ArkTS语法装饰器(下) 【鸿蒙】HarmonyOS NEXT应用开发快速入门教程之布局篇(上) 文…...

使用 Nginx 和 Gunicorn 部署 Flask 项目详细教程
使用 Nginx 和 Gunicorn 部署 Flask 项目详细教程 在这篇文章中,我们将介绍如何使用 Nginx 和 Gunicorn 来部署一个 Flask 项目。这种部署方式非常适合在生产环境中使用,因为它能够提供更好的性能和更高的稳定性。 目录 Flask 项目简介环境准备Gunico…...

linux中bashrc和profile环境变量在Shell编程变量的传递作用
在 Linux 系统中,.bashrc文件和.profile文件都是用于配置用户环境的重要文件,它们之间有以下关联: 一、作用相似性 环境设置:两者都用于设置用户的环境变量和启动应用程序的配置。例如,它们可以定义路径变量…...
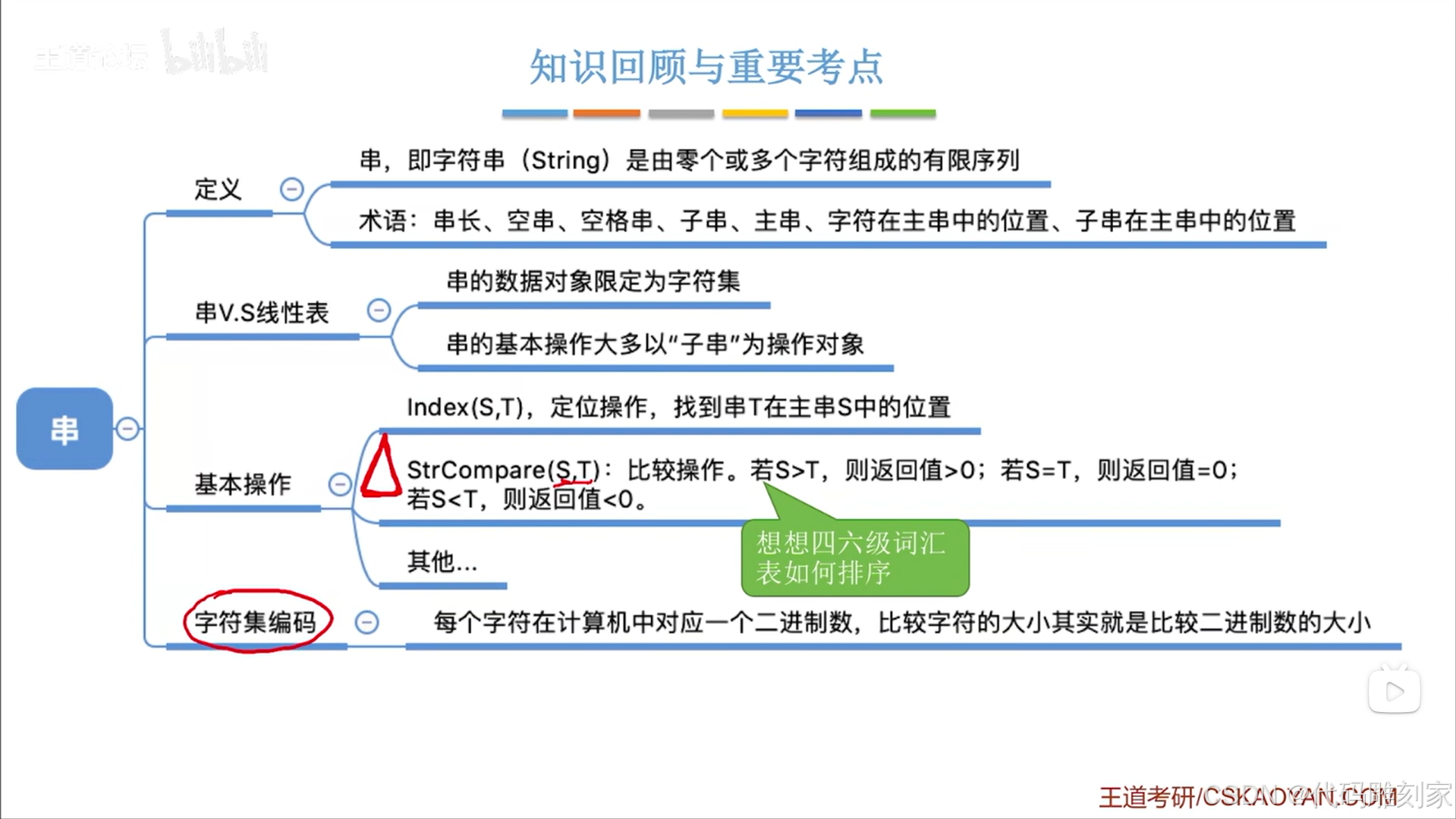
数据结构-4.2.串的定义和基本操作
一.串的定义: 1.单/双引号不是字符串里的内容,他只是一个边界符,用来表示字符串的头和尾; 2.空串也是字符串的子串,空串长度为0; 3.字符的编号是从1开始,不是0; 4.空格也是字符&a…...
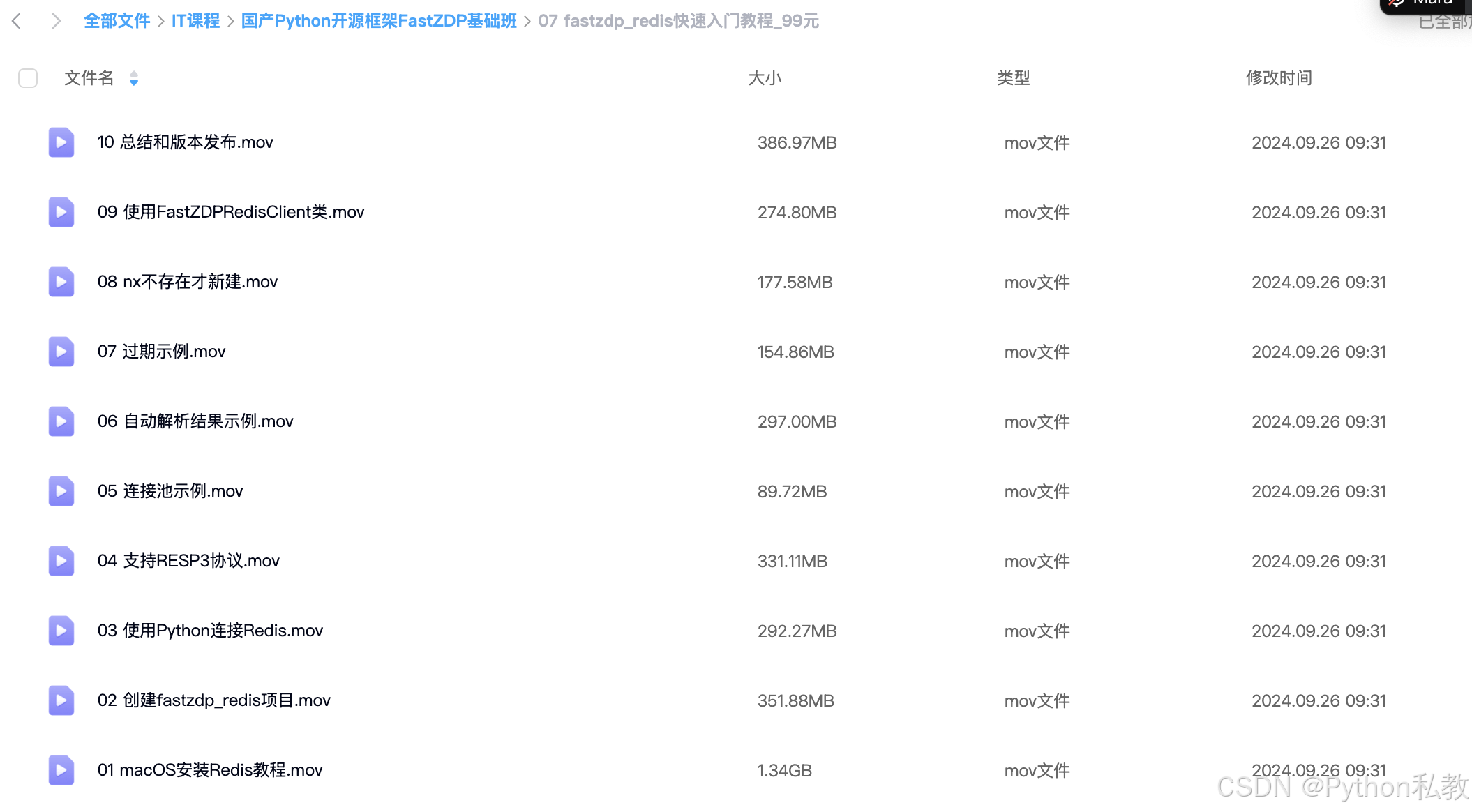
fastzdp_redis第一次开发, 2024年9月26日, Python操作Redis零基础快速入门
提供完整录播课 安装 pip install fastzdp_redisPython连接Redis import redis# 建立链接 r redis.Redis(hostlocalhost, port6379, db0)# 设置key r.set(foo, bar)# 获取key的值 print(r.get(foo))RESP3 支持 简单的理解: 支持更丰富的数据类型 参考文档: https://blog.c…...
文件名:\\?\C:\Windows\system32\inetsrv\config\applicationHost.config错误:无法写入配置文件
文件名: \\?\C:\Windows\system32\inetsrv\config\applicationHost.config 错误:无法写入配置文件 解决办法: 到C:\inetpub\history中找到最近一次的【CFGHISTORY_00000000XX】文件,点击进去找到applicationHost.config文件,用其覆盖C:\Win…...

Optiver股票大赛Top2开源!
Optiver股票大赛Top2开源! ↑↑↑关注后"星标"kaggle竞赛宝典 作者:杰少 Optiver第二名方案解读 简介 Optiver竞赛已经于今天结束了,竞赛也出现了极端情况,中间断崖式的情况,在Kaggle过往的竞赛中&#…...

Maven 实现依赖统一管理
Maven 实现依赖统一管理主要是通过两个关键机制:pom.xml 文件中的 <dependencies> 节点用于声明项目依赖,以及通过继承(Inheritance)和聚合(Aggregation)功能来统一管理和组织这些依赖。此外…...
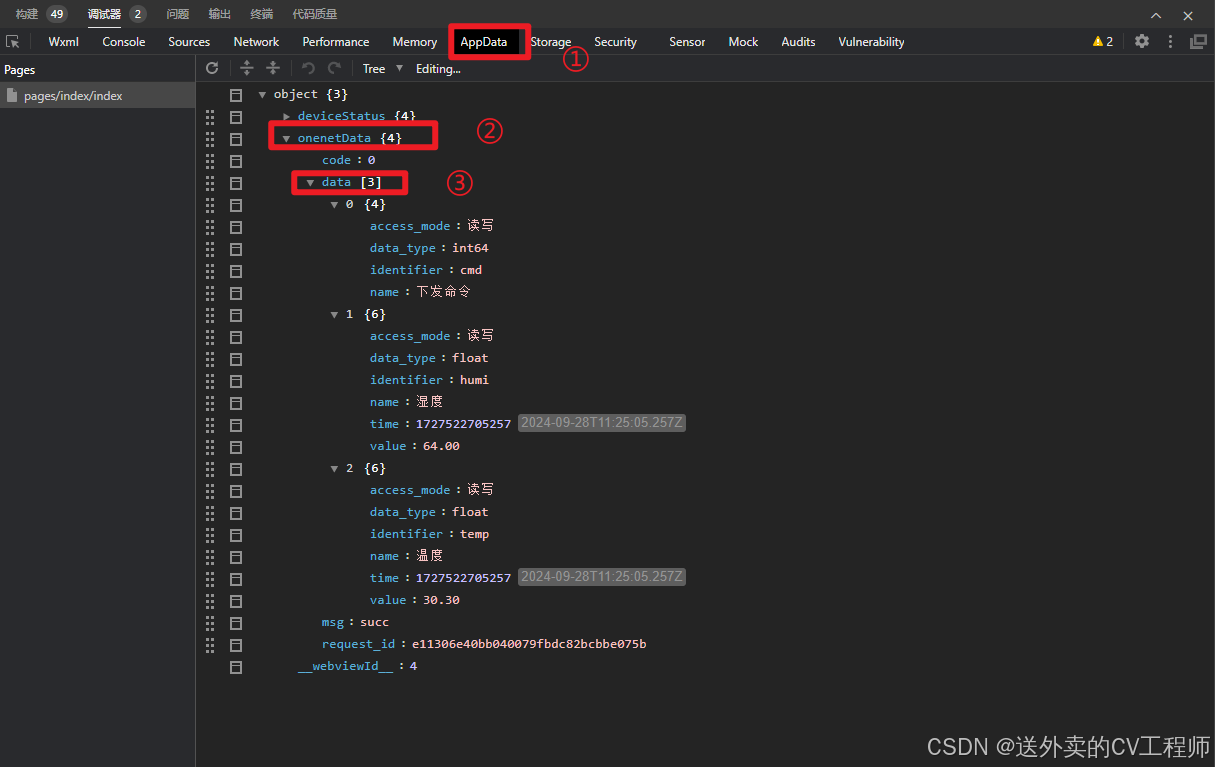
【最新】微信小程序连接onenet——stm32+esp8266+onenet实现查看温湿度,控制单片机
微信小程序——stm32esp8266onenet实现查看温湿度,控制单片机 (最新已验证)stm32 新版 onenet dht11esp8266/01s mqtt物联网上报温湿度和控制单片机(保姆级教程) :↓↓👇 👇 👇 👇…...
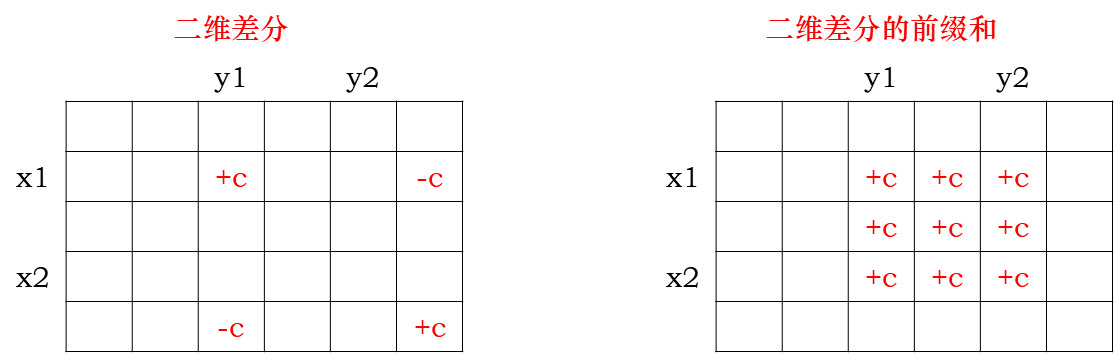
差分(续前缀和)(含一维二维)
题目引入 开发商小 Q 买下了一条街,他想在这条街的一边盖房子。 街道可以抽象为一条数轴,而小 Q 只会在坐标在 1~n 的范围内盖房子。 首先,小 Q 将街上坐标在 1∼ 𝑛1∼ n 范围内的物体全部铲平。也就是说,在正式动工盖…...
【STM32-HAL库】自发电型风速传感器(使用STM32F407ZGT6)(附带工程下载链接)
一、自发电型风速传感器介绍 自发电型风速传感器,也称为风力发电型风速传感器或无源风速传感器,是一种不需要外部电源即可工作的风速测量设备。这种传感器通常利用风力来驱动内部的发电机构,从而产生电能来供电测量风速的传感器部分。以下是自…...

【计算机毕业设计】springboot就业信息管理系统
就业信息管理系统 摘 要 随着信息化时代的到来,管理系统都趋向于智能化、系统化,就业信息管理系统也不例外,但目前国内仍都使用人工管理,市场规模越来越大,同时信息量也越来越庞大,人工管理显然已无法应对时…...
实用工具推荐---- PDF 转换
直接上链接:爱PDF |面向 PDF 爱好者的在线 PDF 工具 (ilovepdf.com) 主要功能如下: 全免费!!!!...

安宝特案例 | 某知名日系汽车制造厂,借助AR实现智慧化转型
案例介绍 在全球制造业加速数字化的背景下,工厂的生产管理与设备维护效率愈发重要。 某知名日系汽车制造厂当前面临着设备的实时监控、故障维护,以及跨地域的管理协作等挑战,由于场地分散和突发状况的不可预知性,传统方式已无法…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
