当前位置：首页 > news >正文

选读算法导论5.2 指示器随机变量

news 2025/12/16 23:49:33

为了分析包括包括雇佣分析在内的许多算法，我们将使用指示器随机变量，它为概率和期望之间的转换提供了一个便利的方法，给定一个样本空间S和事件A，那么事件A对应的指示器随机变量：

Xa = 1 如果A发生
　　 0 如果A没有发生

E[Xa] = Pr{A}

1.指示器随机变量将所求的随机变量X分解成了许多单个的事件，对于每一个事件一一的求期望，加起来即可。

2.注意随机变量指示器怎么用，实际上就是将求一个随机变量的期望，分解到一个个具体的事件，每一个小事件的期望往往容易求，所有小事件的期望加起来就是总得期望。其实是从另一个角度看问题。

转载于dianlu7964的算法导论5.2 指示器随机变量

下面我通过列举题目通过运用这种方法来更快理解

Bubble Sort - 洛谷

给定n，求所有[1,n]排列中逆序对个数的平均值，以分数形式输出。

还可以转化题意为期望逆序对个数是多少?

单个事件就是单独一个对是逆序对 $Pi=\frac{1}{2}$

$E=\sum Ei$

那么总共有几个呢，应该是 $\binom{n}{2}$

$E=\binom{n}{2}*\frac{1}{2}=\frac{n*(n-1)}{4}$

Game on Tree - 洛谷

给定一棵有根树，结点编号从 11 到 nn。根结点为 11 号结点。

对于每一次操作，等概率的选择一个尚未被删去的结点并将它及其子树全部删去。当所有结点被删除之后，游戏结束；也就是说，删除 11 号结点后游戏即结束。

要求求出删除所有结点的期望操作次数。

单个事件选择i节点可以直接删除树，因为选了祖先节点就不会选i节点了，因此我们选i节点要比祖先节点先选，这个概率是 $Pi=\frac{1}{depth i}$

即 $E=\sum \frac{1}{depthi}$

[国家集训队] 单选错位 - 洛谷

lc的期望就很明显是这种方法求得，每个道题对的概率是 $Pi=\frac{1}{ai}$ ,那么 $E=\sum \frac{1}{ai}$

gx的期望只是多了一个限制条件 ai,ai+1的关系

1. $ans[i]=ans[i+1]$ $Pi=\frac{1}{ai}$

2. $ans[i]>ans[i+1]$

gx可以答对的部分只能是 $\frac{ai+1}{ai}$ ,概率为 $Pi=\frac{ai+1}{ai}*\frac{1}{ai+1}=\frac{1}{ai}$

3. $ans[i]<ans[i+1]$

gx可以答对的部分只能是 $\frac{ai}{ai+1}$ ,概率为 $Pi=\frac{ai}{ai+1}*\frac{1}{ai}=\frac{1}{ai+1}$

因此 $Pi=\frac{1}{max(ai,ai+1)}$ ，即 $E=\sum \frac{1}{max(ai,ai+1)}$

未完待续

选读算法导论5.2 指示器随机变量

为了分析包括包括雇佣分析在内的许多算法，我们将使用指示器随机变量，它为概率和期望之间的转换提供了一个便利的方法，给定一个样本空间S和事件A，那么事件A对应的指示器随机变量： Xa 1 如果A发生　　 0 如果…...

编程日记 2024/10/2 16:18:23

大数据-154 Apache Druid 架构与原理详解基础架构、架构演进

点一下关注吧！！！非常感谢！！持续更新！！！ 目前已经更新到了： Hadoop（已更完）HDFS（已更完）MapReduce（已更完&am…...

编程日记 2024/10/2 16:12:17

centos9 nginx 版本

centos9 安装 ssh -V OpenSSH_8.7p1, OpenSSL 3.2.2 4 Jun 2024 openssl version OpenSSL 3.2.2 4 Jun 2024 (Library: OpenSSL 3.2.2 4 Jun 2024) sudo yum install nginx Installing:nginx x86_64 2:1.20.1…...

编程日记 2024/10/2 16:09:14

https访问报错：net::ERR_CERT_DATE_INVALLD

目录简介异常排查原因解决补充简介访问https资源出现报错异常排查将地址拿到浏览器进行访问，可以很清晰的看到出现该问题的原因原因 1、SSL证书已过期 2、服务器日期不准，不在证书有效期解决 1、重新申请SSL证书，并配置 2、校正…...

编程日记 2024/10/2 16:07:12

cat用来查看文件内容、合并文件，或者将文件内容输出到终端

cat 是 Unix 和 Linux 系统中的一个命令，它的名称来源于 “concatenate”（连接），主要用来查看文件内容、合并文件，或者将文件内容输出到终端。常用用法查看文件内容 cat filename输出 filename 的内容到终端中。例…...

编程日记 2024/10/2 16:04:09

基于ssm大学生自主学习网站的设计与实现

文未可获取一份本项目的java源码和数据库参考。 1、毕业论文（设计）的背景及意义： （1）研究背景目前，因特网是世界上最大的计算机互联网络，它通过网络设备将世界各地互相独立的不同规模的局域…...

编程日记 2024/10/2 16:03:08

C++基础补充(01)C++11基于范围的for循环

文章目录 1. 基本语法1.1 decalaration默认获取值引用&自动类型推导（auto） 1.2 container数组STL容器初始化列表自定义类型返回容器的函数 2. 其他示例2.1 遍历数组2.2 遍历vector，并修改元素2.3 使用常量引用遍历，防止容器中…...

编程日记 2024/10/2 16:02:07

检查可用的数据库驱动： // iteator all database driverQStringList drivers QSqlDatabase::drivers();QStringList::iterator it;for (it drivers.begin(); it ! drivers.end(); it){qDebug() << *it;} qt6 自带pg数据库驱动： pro文件加个说明&…...

编程日记 2024/10/2 16:01:06

【PostgreSQL】提高篇——公用表表达式（CTE）和窗口函数

在这篇文章中，我将详细介绍 PostgreSQL 中的公用表表达式（CTE）和窗口函数，帮助你理解如何使用它们进行复杂的数据分析。我将通过具体的示例来演示这些概念的实际应用，并在每个示例中提供详细的解释和注释。 1. 公用表…...

编程日记 2024/10/2 16:00:05

【min25筛】【CF2020F】Count Leaves

题目定义 f ( n , 0 ) 1 f(n,0)1 f(n,0)1， f ( n , d ) ∑ k ∣ n f ( k , d − 1 ) f(n,d)\sum_{k|n}f(k,d-1) f(n,d)∑k∣nf(k,d−1) 给出 n , k , d n,k,d n,k,d，你需要求出: ∑ i 1 n f ( i k , d ) m o d ( 1 0 9 7 ) \sum_{i1}^n f(i^k…...

编程日记 2024/10/2 15:51:58

【d57】【sql】1661. 每台机器的进程平均运行时间

思路一方面考察自连接，另一方面考察group by 这里主要说明 group by 用法： 1.在 SQL 查询中，GROUP BY 子句用于将结果集中的行分组，目的通常就是对每个组应用聚合函数（如 SUM(), AVG(), MAX(), MIN(), COUNT() 等…...

编程日记 2024/10/2 15:45:52

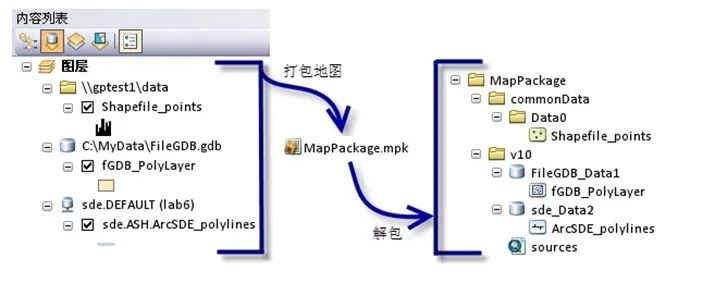
ArcGIS共享数据的最佳方法（不丢可视化、标注等各类显示信息一样带）

今天我们介绍一下ArcGIS数据共享的几个小妙招我们时常要把数据发给对方，特别是很多新手朋友要将shp发给对方时只是发送了shp后缀的文件，却把shp的必要组成文件dbf、shx等等给落下了。还有很多朋友给图层做好了符号化标注，但是数据一发给别…...

编程日记 2024/10/2 15:44:50

小程序this.getOpenerEventChannel()当前页面与navigateTo页面之间数据通信

this.getOpenerEventChannel() 是微信小程序中获取页面打开它的页面事件通道的方法。但是，这个方法只在页面是被wx.navigateTo打开的情况下才能使用。如果页面是通过其他方式打开的，比如wx.redirectTo，那么就无法使用这个方法。解决方案&…...

编程日记 2024/10/2 15:43:49

调用飞书接口导入供应商bug

1、业务背景财务这边大部分系统都是供应商项目，由于供应商的研发人员没有飞书项目的权限，涉及到供应商系统需求财务这边都是通过多维表格进行bug的生命周期管理如图： 但多维表格没有跟飞书项目直接关联，测试组做bug统计的时候无…...

编程日记 2024/10/2 15:40:47

《深度学习》OpenCV 角点检测、特征提取SIFT 原理及案例解析

目录一、角点检测 1、什么是角点检测 2、检测流程 1）输入图像 2）图像预处理 3）特征提取 4）角点检测 5）角点定位和标记 6）角点筛选或后处理（可选） 7）输出结果 3、邻域…...

编程日记 2024/10/2 15:39:46

golang grpc初体验

grpc 是一个高性能、开源和通用的 RPC 框架，面向服务端和移动端，基于 HTTP/2 设计。目前支持c、java和go，分别是grpc、grpc-java、grpc-go，目前c版本支持c、c、node.js、ruby、python、objective-c、php和c#。grpc官网 grpc-go P…...

编程日记 2024/10/2 15:37:44

基于小程序+Vue + Spring Boot的进销存库存出库入库统计分析管理系统

目录一、项目背景及需求分析 1. 项目背景 2. 需求分析二、系统架构设计 1. 技术选型 2. 模块划分三、数据库设计数据库表结构四、前端实现五、后端实现 1. RESTful API设计 2. 数据库操作六、安全性和性能优化 1. 安全性 2. 性能优化七、测试与部署 1. …...

编程日记 2024/10/2 15:35:41

【数据结构与算法】时间复杂度和空间复杂度例题

文章目录时间复杂度常数阶时间O(1)对数阶时间O(logN)线性阶时间O(n)线性对数阶时间O(nlogN)平方阶时间O(n*n) 空间复杂度常量空间O(1)线性空间O(n)二维空间O(n*n)递归空间时间复杂度常数阶时间O(1) 代码在执行的时候，它消耗的时间并不随着某个变量的增长而增长…...

编程日记 2024/10/2 15:34:41

停止模式下USART为什么可以唤醒MCU？

在MCU的停止模式下，USART之类的外设时钟是关闭的，但是USART章节有描述到在停止模式下可以用USART来对MCU进行唤醒： 大家是否会好奇在外设的时钟被关闭的情况下，USART怎么能通过接收中断或者唤醒事件对MCU进行唤醒的呢&#xff1…...

编程日记 2024/10/2 15:32:39

Web安全 - 路径穿越（Path Traversal）

文章目录 OWASP 2023 TOP 10导图定义路径穿越的原理常见攻击目标防御措施输入验证和清理避免直接拼接用户输入最小化权限日志监控 ExampleCode漏洞代码：路径穿越攻击案例漏洞说明修复后的安全代码代码分析其他不同文件系统下的路径穿越特性Windows系统类Unix系统&a…...

编程日记 2024/10/2 15:30:37

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度

一、引言：多云环境的技术复杂性本质企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时，基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套：跨云网络构建数据…...

编程新知 2025/12/12 9:42:53

装饰模式（Decorator Pattern）重构java邮件发奖系统实战

前言现在我们有个如下的需求，设计一个邮件发奖的小系统， 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件装饰器模式（Decorator Pattern）允许向一个现有的对象添加新的功能，同时又不改变其…...

编程新知 2025/12/15 19:31:01

微信小程序之bind和catch

这两个呢，都是绑定事件用的，具体使用有些小区别。官方文档： 事件冒泡处理不同 bind：绑定的事件会向上冒泡，即触发当前组件的事件后，还会继续触发父组件的相同事件。例如，有一个子视图绑定了b…...

编程新知 2025/12/10 15:29:40

FastAPI 教程：从入门到实践

FastAPI 是一个现代、快速（高性能）的 Web 框架，用于构建 API，支持 Python 3.6。它基于标准 Python 类型提示，易于学习且功能强大。以下是一个完整的 FastAPI 入门教程，涵盖从环境搭建到创建并运行一个简单的…...

编程新知 2025/10/16 7:51:26

定时器任务——若依源码分析

分析util包下面的工具类schedule utils： ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类，封装了定时任务的创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz，先构建任务的 JobD…...

编程新知 2025/12/14 17:25:48