AcWing 802. 区间和(离散化算法,python)
本篇博客详细讲解一下离散化知识点,通过讲解和详细列题带大家掌握离散化。
题目:
原题链接:https://www.acwing.com/problem/content/description/804/
假定有一个无限长的数轴,数轴上每个坐标上的数都是 0。
现在,我们首先进行 n 次操作,每次操作将某一位置 x 上的数加 c。
接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l,r] 之间的所有数的和。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含两个整数 x 和 c。
再接下来 m 行,每行包含两个整数 l 和 r。
输出格式
共 m 行,每行输出一个询问中所求的区间内数字和。
数据范围
− 1 0 9 ≤ x ≤ 1 0 9 -10^9≤x≤10^9 −109≤x≤109,
1 ≤ n , m ≤ 1 0 5 1≤n,m≤10^5 1≤n,m≤105,
− 1 0 9 ≤ l ≤ r ≤ 1 0 9 −10^9≤l≤r≤10^9 −109≤l≤r≤109,
− 10000 ≤ c ≤ 10000 −10000≤c≤10000 −10000≤c≤10000
输入样例:
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例:
8
0
5
什么是前缀和?(会此算法可以跳过不看)
一维前缀和&一维差分(下篇讲解二维前缀和&二维差分)(超详细,python版,其他语言也很轻松能看懂)
什么是离散化?
本题猛的一看似乎就是一道前缀和的模板题,但需要注意到这里所谓的“坐标”的范围较大,范围在 − 1 0 9 ≤ x ≤ 1 0 9 -10^9≤x≤10^9 −109≤x≤109,为了存下被修改的点的数据,如果将它们的坐标作为数组的下标就需要开一个 2 ∗ 1 0 9 2*10^9 2∗109大小的数组,肯定会爆内存,况且这里的坐标还有负值,不方便进行存储。
所以要提出一个新的能方便快捷存数据的算法——离散化。
离散化的内存优化思路是只存储那些被用到的点(在这里指的是“被加了值的点”以及“要查询区间的两个端点”),然后利用一些较小的值来代替它们的坐标进行索引,并最终保持它们的相对位置。
举个例子:对于“被用到的点”只有四个:1、11、886、320001,如果用传统的存储方式要开1~320001个连续的存储空间,但其实没必要,因为会浪费掉了很多没有用到的空间。其实它们的相对位置可以分别用1(1)、2(11)、3(886)、4(320001)来替代,进而只需要开1~4个连续的存储空间并且全部用上;反观此题的数据量,操作次数决定要存点的个数,n、m均小于等于 1 0 5 10^5 105,所以“被用到的点”最多为 n + 2 m = 3 ∗ 1 0 5 n + 2m =3 *10^5 n+2m=3∗105个 ,也即内存从 2 ∗ 1 0 9 2 * 10^9 2∗109优化到了 3 ∗ 1 0 5 3 * 10^5 3∗105,整整少了4个数量级!
因此,点的存储位置变为连续,但其表示的值却为离散,故而称其被离散化。
如何离散化?(题解)
为了能够将较大的坐标点及其该坐标点上的数值存储下来,就需要使用两个映射:
- total_num(数组):用来存放题目中用到的坐标点,也就是题中的x, l, r,初始值为空数组。total_num数组表示坐标到相对位置的映射:先将题目中输入样例给出的坐标点全都放入(append)total_num数组后,进行一遍排序和去重,这样就必能保证小的坐标位置在前,大坐标在后,此时下标就是它们新的“相对位置”。
- a(数组):用来存放离散化后的坐标的值的变化,初始范围为 3 ∗ 1 0 5 + 10 3 * 10^5 + 10 3∗105+10 (n + 2m 最大为 3 ∗ 1 0 5 3 * 10^5 3∗105)。表示相对位置到坐标点上的数值的映射:拿到坐标点的相对位置new_x后,a[new_x] += c就存下了坐标点的数据了。
这里还需要定义add_num数组用来存放整数(x, c),定义query_num数组,用来存放询问的区间(l, r)
再定义a的前缀和数组s,预处理完后利用s[r] - s[l - 1]就能得到 [l,r] 区间和了。
下面来详细讲解一下各数组的作用和具体实现方法:
首先初始化各个数组,其中a数组和s数组的长度为 3 ∗ 1 0 5 + 10 3 * 10^5 + 10 3∗105+10,值为0,其余数组初始为空。
total_num数组为何除了要存被改动点的坐标x还要存储查询区间的两端点l和r呢?
主要是因为后续要通过s[r] - s[l - 1]来获取到区间和,而必须将它们在坐标轴上的情况也存下来才能知道这个区间的情况,因而它也算作“被用到的点”。
那么被改动点(x, c)和查询端点(l, r)分别还要再放到add_num和query_num里方便处理。
具体的存储情况还可以下图为例:
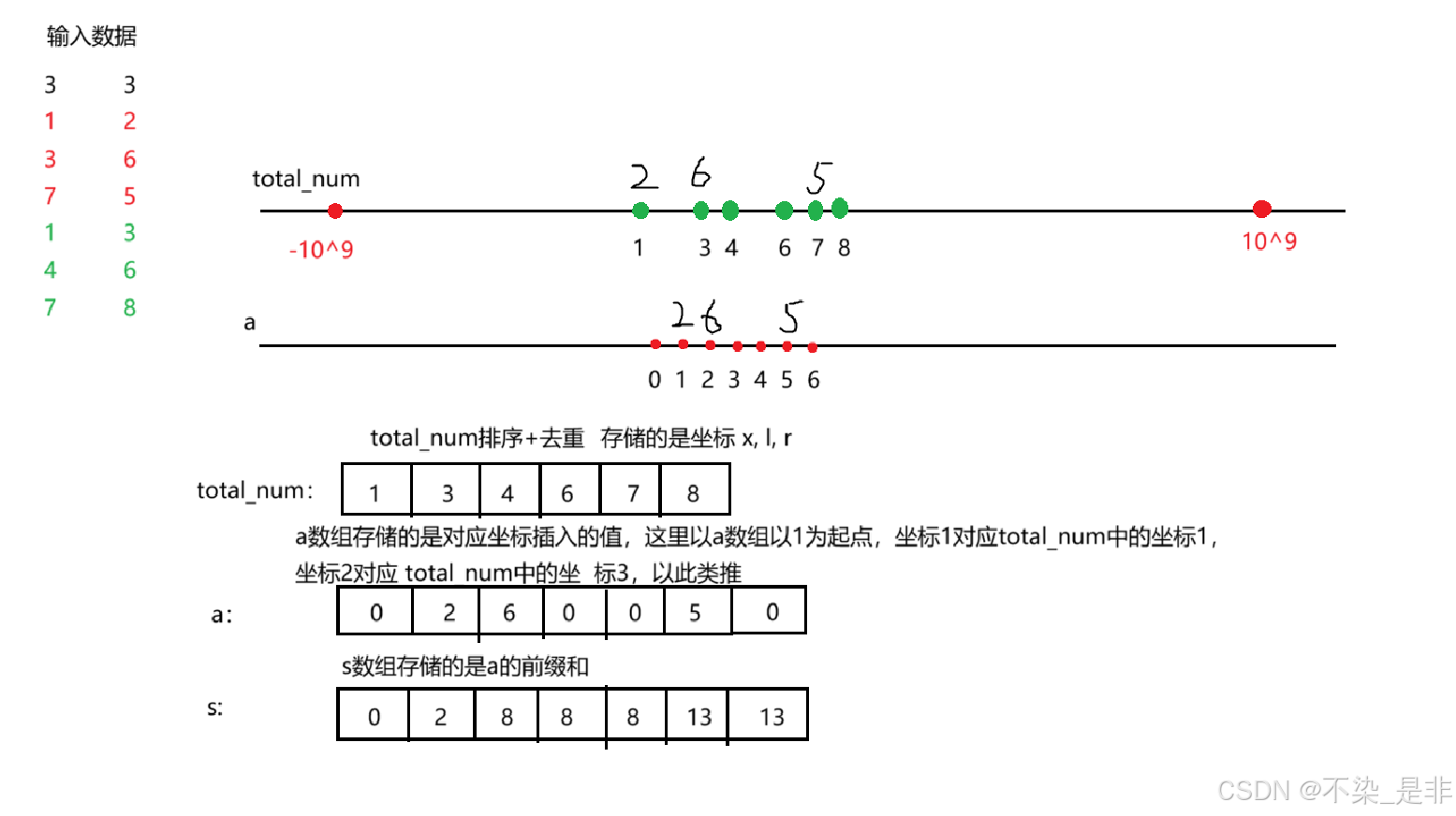
这里还有一个难点就是如何进行离散化?也就是如何把total_num数组映射到a数组上?这里需要借用二分来进行插入操作,二分的初始左端点 l 为0,右端点 r 为total_num数组的长度减一,mid = (l+r) // 2,传入参数是x(这里的x是toal_num里的数值,需要对total_num进行遍历并挨个把total_num中的值映射到a数组中),只要total_num[mid] <= x,那么r = mid 否则 l = mid + 1,最后返回值是 l + 1。
为什么返回的是 l + 1 呢?因为a数组和s数组的下标是从1开始的(下标从1开始是方便处理前缀和),所以这里需要进行+1操作。
下面给出详细代码和注释:
# 读取输入的n和m,分别表示添加操作的数量和查询操作的数量
n, m = map(int, input().split())
N = 300010
a = [0] * N
s = [0] * N
# 用于存储添加操作的列表,每个元素是一个元组,包含要添加的数值x和对应的增量c
add_num = []
# 用于存储查询操作的列表,每个元素是一个元组,包含查询的区间左端点l和右端点r
query_num = []
# 用于存储所有出现过的坐标
total_num = [] # 读取n个添加操作
for i in range(n): x, c = map(int, input().split()) add_num.append((x, c)) total_num.append(x) # 将x添加到total_num中 # 读取m个查询操作
for i in range(m): l, r = map(int, input().split()) query_num.append((l, r)) total_num.append(l) # 将l添加到total_num中 total_num.append(r) # 将r添加到total_num中 # 对total_num进行排序并去重,得到所有唯一出现过的数值
total_num = list(set(sorted(total_num))) # 定义一个查找函数,用于在total_num中找到数值x映射到a的位置(索引从1开始)
def find(x): l = 0 r = len(total_num) - 1 while l < r: mid = (l + r) // 2 if total_num[mid] >= x: r = mid else: l = mid + 1 return l + 1# 对每个添加操作进行处理,将增量c添加到对应的位置
for x, c in add_num: new_x = find(x) # 找到total_num中x映射到a的位置a[new_x] += c # 将增量c添加到a数组的对应位置 # 计算前缀和数组s
for i in range(1, N): s[i] = s[i - 1] + a[i] # 前缀和公式# 对每个查询操作进行处理,计算并输出区间和
for l, r in query_num: xl = find(l) xr = find(r) print(s[xr] - s[xl - 1])
相关文章:

AcWing 802. 区间和(离散化算法,python)
本篇博客详细讲解一下离散化知识点,通过讲解和详细列题带大家掌握离散化。 题目: 原题链接:https://www.acwing.com/problem/content/description/804/ 假定有一个无限长的数轴,数轴上每个坐标上的数都是 0。 现在,…...
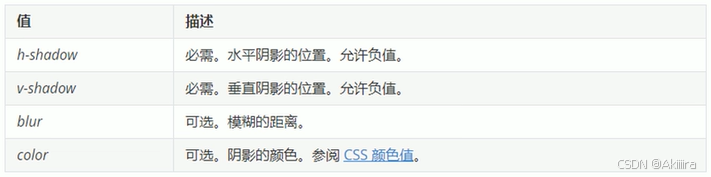
【网页设计】CSS 盒子模型
目标 能够准确阐述盒子模型的 4 个组成部分能够利用边框复合写法给元素添加边框能够计算盒子的实际大小能够利用盒子模型布局模块案例能够给盒子设置圆角边框能够给盒子添加阴影能够给文字添加阴影 1. 盒子模型 页面布局要学习三大核心, 盒子模型, 浮动 和 定位. 学习好盒子模…...
如何通过构建对应的api服务器使Vue连接到数据库
一、安装数据库驱动 在后端安装 MySQL 数据库驱动,比如在 Node.js 环境中可以使用 mysql2 包来连接 MySQL 数据库。在项目目录下运行以下命令安装: npm install mysql2或者使用 yarn: yarn add mysql2二、创建数据库连接模块 创建一个专门…...

新手给视频加字幕的方法有哪些?4种加字幕方法推荐!
在视频制作中,字幕不仅是传递信息的重要手段,还能增强视频的观感和专业性。对于新手来说,如何给视频添加字幕可能是一个挑战。本文将介绍字幕的类型、推荐添加字幕的工具,以及详细添加字幕方法,帮助新手轻松掌握视频字…...

Oracle实际需要用到但常常被忽略的函数
1、Oracle中nvl()与nvl2()函数 函数nvl(expression1,expression2)根据参数1是否为null返回参数1或参数2的值; 函数nvl2(expression1,expression2,expression3)根据参数1是否为null返回参数2或参数3的值 【函数格式】:nvl(expression1,expression2) 若…...

代码随想录算法训练营Day23
局部最优——>全局最优&无反例,试试贪心 455.分发饼干 力扣题目链接:. - 力扣(LeetCode) class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(s);Arrays.sort(g);int gindex0;int count0;…...
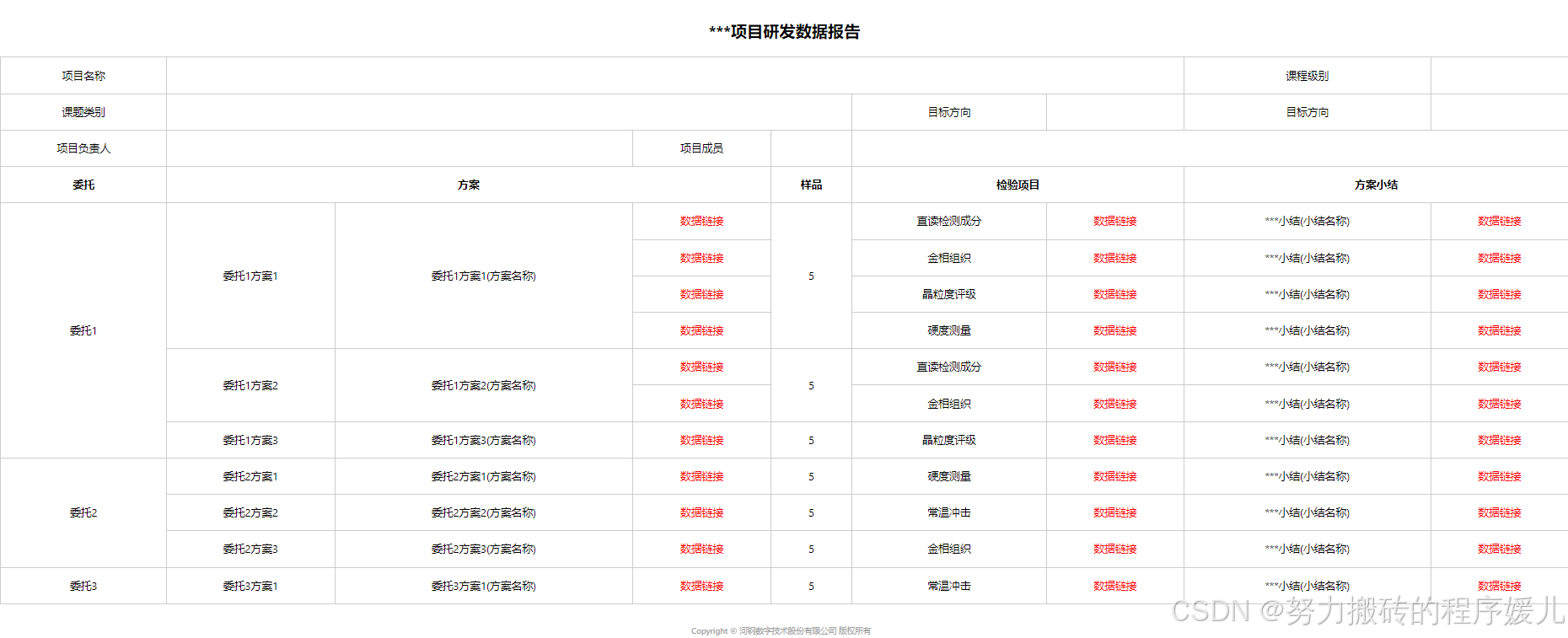
vue使用table实现动态数据报表(行合并)
<template><div class"previewTable"><h2>***项目研发数据报告</h2><table id"previewTable" width"100%"><tr><th>项目名称</th><td colspan"6">{{ resultData.proName }}<…...

YARN调度原理详解
YARN(Yet Another Resource Negotiator)是 Hadoop 集群的资源管理和作业调度框架,它的设计旨在更好地管理和调度 Hadoop 集群中的资源。YARN 解决了传统 Hadoop MapReduce 中资源管理与作业调度紧耦合的问题,使得不同类型的计算任…...

Go-知识泛型
Go-知识泛型 1. 认识泛型1.1 不使用泛型1.2 使用泛型 2. 泛型的特点2.1 函数泛化2.2 类型泛化 3. 类型约束3.1 类型集合3.2 interface 类型集合3.2.1 内置interface类型集合3.2.2 自定义interface类型集合3.2.2.1 任意类型元素3.2.2.2 近似类型元素3.2.2.3 联合类型元素 3.2.3 …...

Qt 如何 发送与解析不定长报文以及数组不定长报文
文章目录 割方式一,采用QDataStream 解析,可直接设定大小端解析,无需自己转换方式二,采用结构体字节对齐方式解析发送接收方割 方式一,采用QDataStream 解析,可直接设定大小端解析,无需自己转换 需要注意的是结构体定义要去掉字节对齐,否则会崩溃,因为由自定义数据结…...

Rust默认使用UTF-8编码来解析源代码文件。如果在代码中包含无法用UTF-8编码表示的字符,编译器会报错!
文章目录 Rust默认编码示例在ANSI编码下中文显示正常的代码在UTF-8编码下将显示不正常在编译时,Rust使用UTF-8编码来解析代码,发现无法用UTF-8编码表示的字符,于是编译器报错 Rust默认编码 Rust 语言默认使用 UTF-8 编码来解析源代码文件。如…...
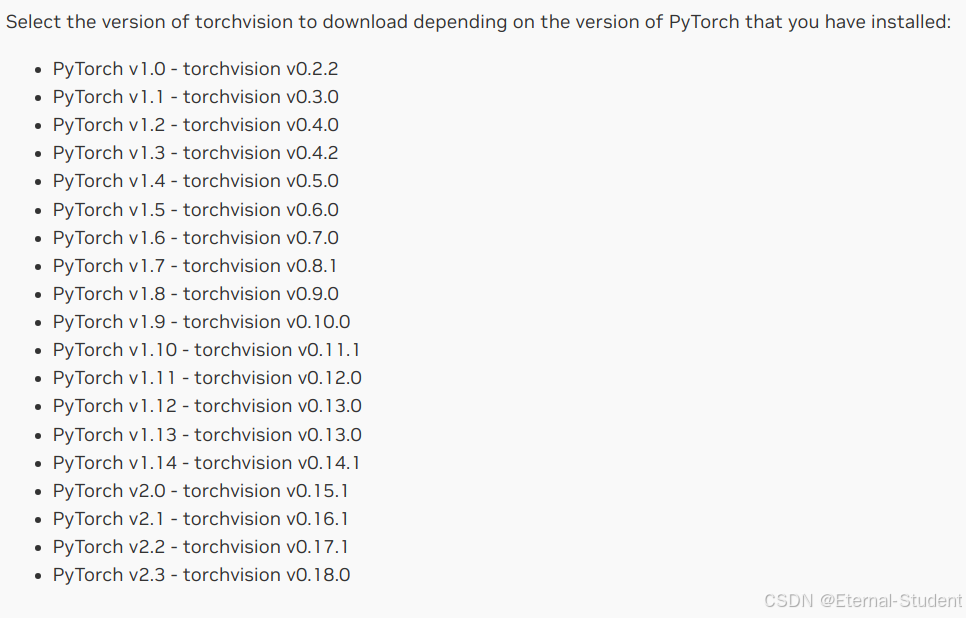
【jeston】torch相关环境安装
参考:玩转NVIDIA Jetson (25)— jetson 安装pytorch和torchvision 我的jeston信息: torch install 安装环境 conda create -n your_env python3.8 conda activate your_envpytorch_for_jeston 安装.whl文件 验证࿱…...

[CR]厚云填补_大型卫星影像去云数据集
AllClear: A Comprehensive Dataset and Benchmark for Cloud Removal in Satellite Imagery Abstract 卫星图像中的云对下游应用构成了重大挑战。当前云移除研究的一个主要挑战是缺乏一个全面的基准和一个足够大和多样化的训练数据集。为了解决这个问题,我们引入了…...
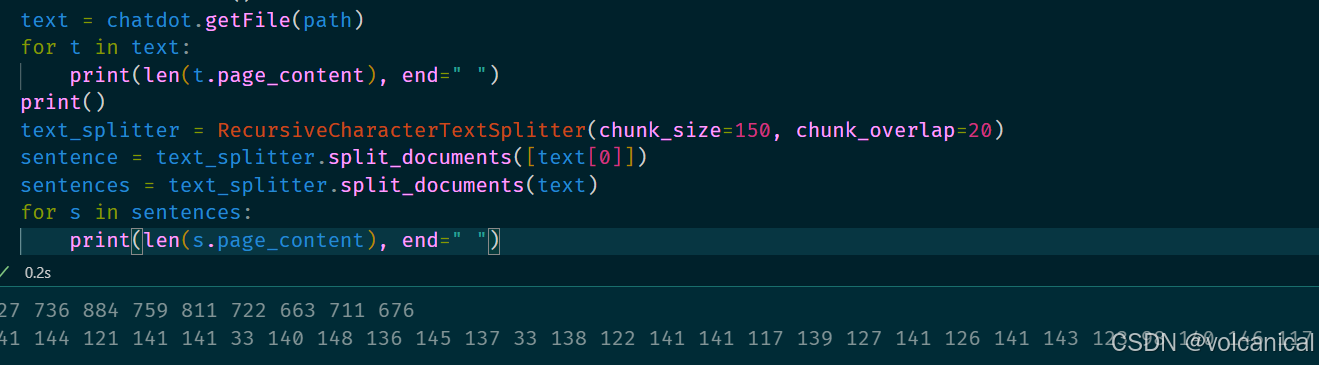
Langchain CharacterTextSplitter无法分割文档问题
在使用Langchain的文档分割器时,使用CharacterTextSplitter拆分文档是,发现返回的文档根本没有变化,即使设置了chunk_size,返回的大小也不符合参数设置。 CharacterTextSplitter设置了150,但是根本没有处理࿰…...

ros service不走是为什么
在ROS(Robot Operating System)中,如果ROS服务(Service)没有正常工作,可能有多种原因。你可以检查以下几点来排查问题: 服务是否正确启动 首先,确保服务节点已经启动并注册了相应的…...
量子计算机的原理与物理实现
量子计算机的原理与物理实现很复杂 指导性原则 首先思考制备一台量子计算机需要些什么? 需要量子比特——二能级量子系统。除了量子计算机需要满足一些物理特性,它还必须要把量子比特绘制到某种初态上,以及测量系统的输出态。 而实验上的挑战…...

SQL Server 常用关键词语法汇总
一、函数 1.1 CAST CAST ( expression AS data_type [ ( length ) ] )expression: 这是你想要转换的数据或表达式。data_type: 目标数据类型,比如 INT, VARCHAR, DATE 等等。(length): 对于某些数据类型(如 CHAR, VARCHAR, BINARY, VARBINARYÿ…...

软件测试工程师面试整理 —— 操作系统与网络基础!
在软件测试中,了解操作系统和网络基础知识对于有效地进行测试工作至关重要。无论是在配置测试环境、调试网络问题,还是在进行性能测试和安全测试时,这些知识都是不可或缺的。 1. 操作系统基础 操作系统(Operating System, OS&am…...

网络安全防御策略:通过限制IP访问提升服务器安全性
标题:网络安全防御策略:通过限制IP访问提升服务器安全性 摘要: 在网络安全领域,服务器被入侵是一场严重的事故。一旦发生这种情况,除了立即采取措施恢复系统外,还需要加强后续的安全防护措施。本文将探讨为…...

Multiprocessing出错没有提示was skipped without notice in python
这个问题可以通过打印返回结果解决。 解决方法 比如 Pool.apply_async(csdnKuangXiaoHU, args=(p, DestFile))改成 Result = Pool.apply_async(csdnKuangXiaoHU, args=...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
