【leetcode|哈希表、动态规划】最长连续序列、最大子数组和
目录
最长连续序列
解法一:暴力枚举
复杂度
解法二:优化解法一省去二层循环中不必要的遍历
复杂度
最大子数组和
解法一:暴力枚举
复杂度
解法二:贪心
复杂度
解法三:动态规划
复杂度
最长连续序列

输入输出示例:

解法一:暴力枚举
两层循环,第一层循环是遍历整个数组;第二层循环的目的是得到最长连续序列时间复杂度极高,效率低下。
1、如果不使用哈希表在枚举过程中查找nums[i]+1时要通过遍历整个数组来进行,因此时间复杂度是O(n^2)
2、使用哈希表枚在举过程中虽说哈希表查找数据的时间复杂度是O(1),但第二次循环仍然需要执行多次,最坏的情况下其时间复杂度也会接近O(n^2)
class Solution {
public:int longestConsecutive(vector<int>& nums) {if(0 == nums.size()) //注意:需要考虑nums为空的情况,此时的最长连续序列就是0return 0;unordered_set<int> hashtable;int max_length = INT_MIN;for(const auto& e:nums) //使用哈希表去重数据hashtable.emplace(e);for(const auto& e:hashtable){int tmp = e;int cnt = 1;while(hashtable.count(++tmp))++cnt;max_length = std::max(max_length,cnt);}return max_length;}
};
复杂度
时间复杂度: O(n^2)
空间复杂度:O(n)
解法二:优化解法一省去二层循环中不必要的遍历
class Solution {
public:int longestConsecutive(vector<int>& nums) {if(0 == nums.size())return 0;int size = nums.size();int max_length = 0;unordered_set<int> hashtable;for(const auto& e:nums)hashtable.insert(e);for(const auto& e:hashtable){if(!hashtable.count(e-1))//只在哈希表中找连续序列的第一个数{int cnt = 1;int tmp = e;while(hashtable.count(++tmp))++cnt;max_length = std::max(max_length,cnt);}}return max_length;}
};
复杂度
时间复杂度:O(n)
空间复杂度:O(n)
最大子数组和

输入输出示例

解法一:暴力枚举
两层循环,定义一个max_sum变量,第二层循环中定义一个tmp变量用来记录第二层循环中连续子数组的和。
lass Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();int max_sum = INT_MIN;for(int i = 0;i<size;++i){int tmp = 0; //用来记录连续子数组的和for(int j = i;j<size;++j){tmp += nums[j];max_sum = std::max(max_sum,tmp);}}return max_sum;}
};该暴力枚举会超出时间限制,不适合。
复杂度
时间复杂度:O(n^2)
空间复杂度:O(1)
解法二:贪心
class Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();int max_sum = nums[0]; //考虑到数组nums只有一个元素的时候,加上题目限制:子数组中至少包含一个元素int tmp = nums[0];for(int i = 1;i<size;++i){if(tmp > 0)tmp += nums[i];elsetmp = nums[i];max_sum = std::max(max_sum,tmp);}return max_sum;}
};复杂度
时间复杂度:O(n)
空间复杂度:O(1)
解法三:动态规划
定义一个dp数组,dp[i]表示以 i 位置结尾的子数组的最大和,利用已经有的dp[i-1]值求dp[i]。

class Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();vector<int> dp(size);//dp[i]表示以i位置结尾的连续子数组的最大和dp[0] = nums[0];int max_sum = dp[0];//当size == 1的时候程序不进入下面循环,直接返回nums[0]for(int i = 1;i<size;++i){if(dp[i-1]>0)dp[i] = dp[i-1] + nums[i];elsedp[i] = nums[i];max_sum = std::max(max_sum,dp[i]);}return max_sum;}
};复杂度
时间复杂度:O(n)
空间复杂度:O(n)
使用滚动数组将空间复杂度优化为O(1):
class Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();//vector<int> dp(size);//dp[i]表示以i位置结尾的连续子数组的最大和int dp1 = nums[0];int dp2 = 0;int max_sum = dp1;for(int i = 1;i<size;++i){if((dp1+nums[i]) > nums[i])dp2 = dp1 + nums[i];elsedp2 = nums[i];max_sum = std::max(max_sum,dp2);dp1 = dp2;//更新dp1}return max_sum;}
};相关文章:

【leetcode|哈希表、动态规划】最长连续序列、最大子数组和
目录 最长连续序列 解法一:暴力枚举 复杂度 解法二:优化解法一省去二层循环中不必要的遍历 复杂度 最大子数组和 解法一:暴力枚举 复杂度 解法二:贪心 复杂度 解法三:动态规划 复杂度 最长连续序列 输入输…...

【人工智能】掌握深度学习中的时间序列预测:深入解析RNN与LSTM的工作原理与应用
深度学习中的循环神经网络(RNN)和长短时记忆网络(LSTM)在处理时间序列数据方面具有重要作用。它们能够通过记忆前序信息,捕捉序列数据中的长期依赖性,广泛应用于金融市场预测、自然语言处理、语音识别等领域…...

今日开放!24下软考机考「模拟练习平台」操作指南来啦!
2024年下半年软考机考模拟练习平台今日开放,考生可以下载模拟作答系统并登录后进行模拟练习,熟悉答题流程及操作方法。 一、模拟练习时间 2024年下半年软考机考模拟练习平台开放时间为2024年10月23日9:00至11月6日17:00,共15天。 考生可以在…...

合并.md文档
需求:将多个.md文档合并成一个.md文档。 方法一:通过 type 命令 参考内容:多个md文件合并 步骤: 把需要合并的 .md 文档放入到一个文件夹内。修改需要合并的 .md 文档名,可以在文档名前加上 1.2.3 来表明顺序&#x…...

10月18日笔记(基于系统服务的权限提升)
系统内核漏洞提权 当目标系统存在该漏洞且没有更新安全补丁时,利用已知的系统内核漏洞进行提权,测试人员往往可以获得系统级别的访问权限。 查找系统潜在漏洞 手动寻找可用漏洞 在目标主机上执行以下命令,查看已安装的系统补丁。 system…...

【STM32 Blue Pill编程实例】-控制步进电机(ULN2003+28BYJ-48)
控制步进电机(ULN2003+28BYJ-48) 文章目录 控制步进电机(ULN2003+28BYJ-48)1、步进电机介绍2、ULN2003步进电机驱动模块3、硬件准备及接线4、模块配置3.1 定时器配置3.2 ULN2003输入引脚配置4、代码实现在本文中,我们将介使用 STM32Cube IDE 使用 ULN2003 电机驱动器来控制28B…...

监督学习、无监督学习、半监督学习、强化学习、迁移学习、集成学习分别是什么对应什么应用场景
将对监督学习、无监督学习、半监督学习、强化学习、迁移学习和集成学习进行全面而详细的解释,包括定义、应用场景以及具体的算法/模型示例。 1. 监督学习 (Supervised Learning) 定义:监督学习是一种机器学习方法,其中模型通过已知的输入数…...

WSL2 Linux子系统调整存储位置
WSL2 默认不支持修改Linux 安装路径,官方提供的方式,只有通过导出、导入的方式实现Linux子系统的迁移。 修改注册表的方式官方不推荐,没有尝试过,仅提供操作方式(自行评估风险,建议备份好数据) 1. 打开 **注册表编辑器…...

Shiro授权
一、定义与作用 授权(Authorization),也称为访问控制,是确定是否允许用户/主体做某事的过程。在Shiro安全框架中,授权是核心组件之一,它负责控制用户对系统资源的访问权限,确保用户只能访问其被…...
算法题总结(十五)——贪心算法(下)
1005、K 次取反后最大化的数组和 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以这种方式修改数组后,返回数组 可…...

《深度学习》【项目】自然语言处理——情感分析 <下>
目录 一、了解项目 1、任务 2、文件内容 二、续接上篇内容 1、打包数据,转化Tensor类型 2、定义模型,前向传播函数 3、定义训练、测试函数 4、最终文件格式 5、定义主函数 运行结果: 一、了解项目 1、任务 对微博评论信息的情感分…...

postgresql是国产数据库吗?
PostgreSQL不是国产数据库。但是PostgreSQL对国产数据库的发展有着重要影响,许多国产数据库产品是基于PostgreSQL进行二次开发的。 PostgreSQL的开源特性也是其受欢迎的重要原因之一。开源意味着任何人都可以查看、修改和使用PostgreSQL的源代码。这使得PostgreSQL…...
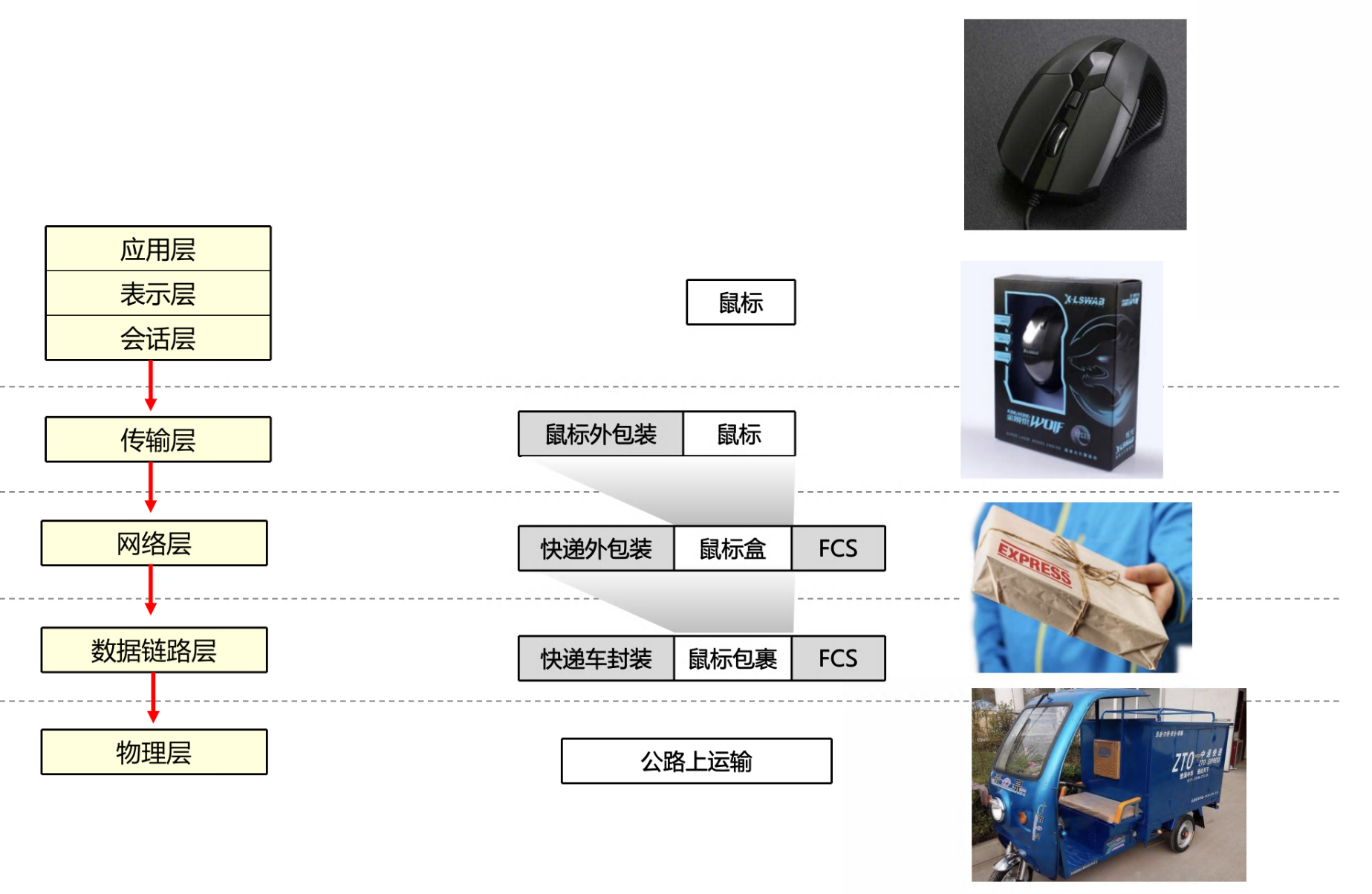
软考——计算机网络概论
文章目录 🕐计算机网络分类1️⃣通信子网和资源子网2️⃣网络拓扑结构3️⃣ 计算机网络分类3:LAN MAN WAN4️⃣其他分类方式 🕑OSI 和 TCP/IP 参考模型1️⃣OSI2️⃣TCP/IP🔴TCP/IP 参考模型对应协议 3️⃣OSI 和 TCP/IP 模型对应…...

01 设计模式-创造型模式-工厂模式
工厂模式(Factory Pattern)是 Java 中最常用的设计模式之一,它提供了一种创建对象的方式,使得创建对象的过程与使用对象的过程分离。 工厂模式提供了一种创建对象的方式,而无需指定要创建的具体类。 通过使用工厂模式…...

ComnandLineRunner接口, ApplcationRunner接口
ComnandLineRunner接口, ApplcationRunner接口 介绍: 这两个接口都有一个run方法,执行时间在容器对象创建好后,自动执行run ( )方法。 创建容器的同时会创建容器中的对象,同时会把容器中的对象的属性赋上值: 举例&…...

Swift用于将String拆分为数组的components与split的区别
根据特定分隔符拆分字符串 在 Swift 中,components(separatedBy:) 和 split(separator:) 都可以用于将字符串拆分为数组,但它们有一些关键区别。下面将从返回值类型、性能和功能等角度进行对比。 1. 返回值类型 components(separatedBy:):…...
)
docker之redis安装(项目部署准备)
创建网络 docker network create net-ry --subnet172.68.0.0/16 --gateway172.68.0.1 redis安装 #创建目录 mkdir -p /data/redis/{conf,data} #上传redis.conf文件到/data/redis/conf文件夹中 #对redis.conf文件修改 # bind 0.0.0.0 充许任何主机访问 # daemonize no #密码 # …...

使用Maven前的简单准备
目录 一、Maven的准备 1、安装jdk1.8或以上版本 2、下载Maven 3、安装Maven 二、Maven目录的分析 三、Maven的环境变量配置 1、设置MAVEN_HOME环境变量 2、设置Path环境变量 3、验证配置是否完成 一、Maven的准备 1、安装jdk1.8或以上版本 jdk的安装 2、下载Maven…...

Java | Leetcode Java题解之第494题目标和
题目: 题解: class Solution {public int findTargetSumWays(int[] nums, int target) {int sum 0;for (int num : nums) {sum num;}int diff sum - target;if (diff < 0 || diff % 2 ! 0) {return 0;}int neg diff / 2;int[] dp new int[neg …...

阅读笔记 Contemporary strategy analysis Chapter 13
来源:Robert M. Grant - Contemporary strategy analysis (2018) Chapter 13 Implementing Corporate Strategy: Managing the Multibusiness Firm Ⅰ Introduction and Objectives 多业务公司 multibusiness firm由多个独立的业务部门组成,如业务单元…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
