当前位置： 首页 > news >正文

基于springboot的网上服装商城推荐系统的设计与实现

news 2026/2/6 6:39:13

基于springboot的网上服装商城推荐系统的设计与实现

开发语言：Java
框架：springboot
JDK版本：JDK1.8
服务器：tomcat7
数据库：mysql 5.7
数据库工具：Navicat11
开发软件：idea

源码获取：
：https://gitee.com/ss-i-gg/Springboot-Online-Clothing-Store-Recommendation-System/blob/master/springboot%E7%BD%91%E4%B8%8A%E6%9C%8D%E8%A3%85%E5%95%86%E5%9F%8E%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E6%BA%90%E7%A0%81.zip
或者https://download.csdn.net/download/weixin_46115961/89901325

项目介绍:
后端框架使用Springboot+mybatis
前端框架使用Vue+hrml
数据库使用mysql

数据库表设计
在这里插入图片描述
项目开发结构
在这里插入图片描述
系统功能展示
前端用户系统
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
后台管理系统
在这里插入图片描述

用户管理登录
在这里插入图片描述
管理员登录：
在这里插入图片描述
源码获取：网上服装商城推荐系统源码

相关文章：

基于springboot的网上服装商城推荐系统的设计与实现

基于springboot的网上服装商城推荐系统的设计与实现 开发语言：Java 框架：springboot JDK版本：JDK1.8 服务器：tomcat7 数据库：mysql 5.7 数据库工具：Navicat11 开发软件：idea 源码获取&#xf…...

编程日记 2024/10/25 5:25:37

盘古信息IMS系统助力制造企业释放新质生产力

在全球制造业竞争日益激烈的背景下，提升新质生产力已成为制造企业普遍追求的核心目标。因此，众多制造企业开始对生产流程、管理模式乃至整个企业生态系统进行全面的优化与升级，以期在市场竞争中占据优势地位，迎来更广阔的发展空间…...

编程日记 2024/10/25 5:24:35

ArcGIS 10.8 安装教程

目录 一、ArcGIS10.8二、安装链接三、安装教程四、ArcGIS实战 （一）ArcGIS10.8 1. 概述 ArcGIS 10.8是由美国Esri公司开发的GIS平台，用于处理、分析、显示和管理地理数据，并实现数据共享。它具有新特性和功能，性能更…...

编程日记 2024/10/25 5:23:34

Redis学习笔记（二）--Redis的安装与配置

文章目录 一、Redis的安装1、克隆并配置主机2、安装前的准备工作1.安装gcc2.下载Redis3.上传到Linux 3、安装Redis1.解压Redis2.编译3.安装3.查看bin目录 4、Redis启动与停止1.前台启动2.命令式后台启动3.Redis的停止4.配置式后台启动 二、连接前的配置1、绑定客户端IP2、关闭保…...

编程日记 2024/10/25 5:22:33

软件工程之软件系统设计与软件开发方法

一.软件系统设计 1.体系结构设计就是架构设计，软件设计包含4个方面： 接口（人机界面设计）设计：软件与操作系统、软件与人之间如何交互； 架构（结构）设计：定义软件系统各…...

编程日记 2024/10/25 5:21:26

pip命令行安装pytest 一直报错

其实就是切换不同镜像安装 我最终成功的是阿里云镜像 pip install --trusted-host mirrors.aliyun.com pytest 也可以用其他的 pip install -i https://pypi.org/simple pytest # 或者使用其他的镜像源 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pytest...

编程日记 2024/10/25 5:20:24

如何在Debian操作系统上安装Doker

本章教程，主要介绍如何在Debian 11 系统上安装Docker。主要使用一键安装Docker脚本和一键卸载脚本来完成。 一、安装Docker #!/bin/bashRED\033[0;31m GREEN\033[0;32m YELLOW\033[0;33m BLUE\033[0;34m NC\033[0mCURRENT_DIR$(cd "$(dirname "$0")…...

编程日记 2024/10/25 5:17:16

代码随想录刷题学习日记

仅为个人记录复盘学习历程，解题思路来自代码随想录 代码随想录刷题笔记总结网址:代码随想录 二叉树的迭代遍历(不使用递归实现遍历) 递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，递归是通过栈实现…...

编程日记 2024/10/25 5:16:15

OpenText ALM Octane，为您的 DevOps 管道提供质量保证

实现更高水平的敏捷性、可追溯性和可预测性是一个持续的过程。ALM Octane 可帮助您改进开发和测试流程，从而改善整个软件交付价值流中的工作流程。 产品亮点 对基于软件的创新的需求已经加速，扰乱了几乎每个行业，也改变了我们的生活。快速交…...

编程日记 2024/10/25 5:15:12

【python实操】python小程序之参数化以及Assert（断言）

引言 python小程序之参数化以及Assert（断言） 文章目录 引言一、参数化2.1 题目2.2 代码2.3 代码解释 二、Assert（断言）2.1 概念2.1.1 Assert语句的基本语法：2.1.2 基本断言2.1.3 断言函数参数2.1.4 断言前后状态一致 2…...

编程日记 2024/10/25 5:13:10

探索CSS动画下的按钮交互美学

效果演示 这段代码通过SVG和CSS动画创建了一个具有视觉吸引力的按钮&#xff0c;当用户与按钮交互时&#xff08;如悬停、聚焦或按下&#xff09;&#xff0c;按钮会显示不同的动画效果。 HTML <button class"button"><div class"dots_border"…...

编程日记 2024/10/25 5:11:08

241024-Ragflow离线部署Docker-Rootless环境配置修改

A. 最终效果 B. 文件修改 docker-compose.yml include:- path: ./docker-compose-base.ymlenv_file: ./.envservices:ragflow:depends_on:mysql:condition: service_healthyes01:condition: service_healthyimage: ${RAGFLOW_IMAGE}container_name: ragflow-serverports:- ${…...

编程日记 2024/10/25 5:10:07

网络基础概念：广播域、冲突域与VLAN解析

一、网络基础概念 在现代计算机网络中&#xff0c;广播域、冲突域和虚拟局域网&#xff08;VLAN&#xff09;是网络架构和管理的核心概念。了解这些概念对网络性能优化、流量管理和安全性提升至关重要。 二、广播域 1. 定义 广播域是一个网络逻辑区域&#xff0c;在这个区域…...

编程日记 2024/10/25 5:09:06

【MySQL】C语言连接MySQL数据库3——事务操作和错误处理API

目录 1.MySQL事务处理机制 1.1.autocommit 1.2.autocommit的设置与查看 1.3.使用示例 2.事务操作API 2.1.设置事务提交模式——mysql_autocommit() 2.2.提交事务——mysql_commit() 2.3.事务回滚——mysql_rollback() 3.错误处理的API 3.1.返回错误的描述——mysql_er…...

编程日记 2024/10/25 5:08:04

ARM嵌入式学习--第六天(电子电路基础知识)

电子电路基础知识 -基本元器件 -电阻 电阻&#xff08;Resistance&#xff0c;通常用“R”表示&#xff09;&#xff0c;表示导体对电流的阻碍作用的大小&#xff1b;电阻导体本身的一种特性&#xff1b;超导体没有电阻&#xff0c;作用是用来降压 上拉电阻&#xff1a;将状态…...

编程日记 2024/10/25 5:06:00

JAVA----单例模式

1.单例模式概念&#xff1a; 单例模式是一种设计模式&#xff0c;他的核心是确保一个类只有一个实例&#xff0c;单例模式主要有两种方式&#xff1a;饿汉式与懒汉式 2.饿汉式 饿汉就是一个迫切的意思&#xff0c;类加载就会导致该单实例被创建 饿汉式第一种方式&#xff1a;…...

编程日记 2024/10/25 5:04:58

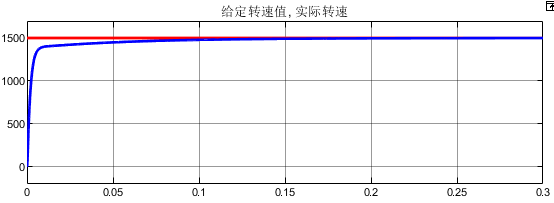
基于递推式最小二乘法的PMSM参数辨识MATLAB仿真模型

微❤关注“电气仔推送”获得资料&#xff08;专享优惠&#xff09; 模型简介 最小二乘法是一种回归估计法&#xff0c;适用于被辨识的参数与系统输出为线性关 系的情况。它是在一定数据量下&#xff0c;基于系统输出误差的平方和最小的准则对参 数进行辨识的方法。此模型通过…...

编程日记 2024/10/25 5:03:57

记录一次部署 k8s 集群无法启动

情况是这样的&#xff0c;k8s 集群&#xff08;v1.31&#xff09;所需要的组件已安装完成&#xff0c;通过 kubeadm init 已经安装部署成功&#xff0c;但是等几分钟&#xff0c;集群组件就一直在重启&#xff0c;查看日志是连接 etcd 超时&#xff0c;所以查看了 etcd 的日志&…...

编程日记 2024/10/25 5:02:56

Linux下MySQL8.x的编译安装与使用

Linux下MySQL的安装与配置 1. 安装环境初始化 1.1 查看是否安装过MySQL 如果使用rpm安装, 检查一下RPM PACKAGE rpm -qa | grep -i mysql # -i 忽略大小写 # 或者 yum list installed | grep mysql如果存在mysql-libs的旧版本包&#xff0c;显示如下 #存在 [rootlocalhost ~]…...

编程日记 2024/10/25 5:01:55

cpuinfo实践记录

py-cpuinfo 是一个用于获取 CPU 信息的 Python 库。它可以帮助你获取 CPU 的详细信息&#xff0c;如 CPU 型号、核心数、频率、缓存大小等。以下是对 py-cpuinfo 模块的详细介绍&#xff1a; 安装 你可以使用 pip 来安装 py-cpuinfo 库&#xff1a; pip install py-cpuinfo …...

编程日记 2024/10/25 4:58:52

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录

ASP.NET Core 是一个跨平台的开源框架&#xff0c;用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录&#xff0c;以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

编程新知 2026/2/6 4:07:25

定时器任务——若依源码分析

分析util包下面的工具类schedule utils&#xff1a; ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类&#xff0c;封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz&#xff0c;先构建任务的 JobD…...

编程新知 2026/1/26 14:24:46

基于数字孪生的水厂可视化平台建设：架构与实践

分享大纲&#xff1a; 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年&#xff0c;数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段&#xff0c;基于数字孪生的水厂可视化平台的…...

编程新知 2025/12/23 17:14:55

css3笔记 （1） 自用

outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size&#xff1a;0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格&#xff…...

编程新知 2025/10/11 5:18:43

安卓基础（aar）

重新设置java21的环境&#xff0c;临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的&#xff1a; MyApp/ ├── app/ …...

编程新知 2026/1/25 8:10:56

华硕a豆14 Air香氛版，美学与科技的馨香融合

在快节奏的现代生活中&#xff0c;我们渴望一个能激发创想、愉悦感官的工作与生活伙伴&#xff0c;它不仅是冰冷的科技工具&#xff0c;更能触动我们内心深处的细腻情感。正是在这样的期许下&#xff0c;华硕a豆14 Air香氛版翩然而至&#xff0c;它以一种前所未有的方式&#x…...

编程新知 2026/1/29 14:27:00

【Go语言基础【13】】函数、闭包、方法

文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数&#xff08;函数作为参数、返回值&#xff09; 三、匿名函数与闭包1. 匿名函数&#xff08;Lambda函…...

编程新知 2025/12/8 19:02:25

使用SSE解决获取状态不一致问题

使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件&#xff0c;这个上传文件是整体功能的一部分&#xff0c;文件在上传的过程中…...

编程新知 2026/1/27 17:00:20

【Kafka】Kafka从入门到实战：构建高吞吐量分布式消息系统

Kafka从入门到实战：构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台，最初由LinkedIn开发，后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理，能够处理来自多个生产者的海量数据，并将这些数据实时传递给消费者。 Kafka核心特…...

编程新知 2025/7/18 7:59:36

链式法则中 复合函数的推导路径 多变量“信息传递路径”

非常好&#xff0c;我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题&#xff0c;统一使用 二重复合函数&#xff1a; z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y))​ 来全面说明。我们会展示其全微分形式&#xff08;偏导…...

编程新知 2026/2/1 23:41:25