动态规划<一>初识动态规划
目录
认识动态规划
LeetCodeOJ练习
斐波那契数列模型
认识动态规划
1.动态规划是一种用于解决优化问题的算法策略。
2.它的核心原理是把一个复杂的问题分解为一系列相互关联的子问题。通过先求解子问题,并且记录这些子问题的解(通常用一个表格之类的存储结构),避免重复计算,然后基于这些子问题的解来构建原问题的解
3.解题步骤
这里通过一道题进行说明一些概念
传送门:LeetCode<1137> 第 N 个泰波那契数
1.创建一个dp表(一般用数组)
2.确定状态表示
状态表示的话,简单理解就是dp表里面的值所代表的含义
对于此题的话,就是dp[i]表示的含义为第i个泰波那契数
该如何确定状态表示:
(1)可以根据题目要求,对于本题就是
(2)经验和题目要求
(3)分析问题的过程中,发现重复子问题
3.确定状态转移方程
简单说就是求出dp[i]等于什么 对于本题就是dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
4.初始化
确定初始状态的值,保证填表时不发生越界
对于此题就是dp[0],dp[1],dp[2]必须初始化,若通过状态转移方程计算的话,就会发生越界
5.填表顺序
确定是从左向右,还是从右向左的顺序填表,确保填写当前状态的时候,所需要的状态已经计算过了,对于本题就是从左向右的顺序
6.返回结果
根据题目要求和具体的状态表示,对于此题就是返回dp[n]
7.空间优化(不是必须)
因为创建dp表,导致空间复杂度为O(N),在这里我们可以用滚动数组进行优化
通过几个变量来降低空间复杂度

当我们依次往后求dp[i]时,前面的一些状态可以舍去,仅仅用中间若干个有效的状态,比如求dp[5]只需要知道dp[4],dp[3],dp[2]就可以了,像这样的情况就可以使用滚动数组来优化

本题具体代码
没有做优化的版本
int tribonacci(int n) {//1.创建dp表//2.初始化//3.填表//4.返回值//处理边界情况if(n==0) return 0;if(n==1 || n==2) return 1;vector<int> dp(n+1);dp[0]=0,dp[1]=dp[2]=1;for(int i=3;i<=n;++i)dp[i]=dp[i-1]+dp[i-2]+dp[i-3];return dp[n];}优化的版本
int tribonacci(int n) {//1.创建dp表//2.初始化//3.填表//4.返回值//处理边界情况if(n==0) return 0;if(n==1 || n==2) return 1;int a=0,b=1,c=1,d=0;for(int i=3;i<=n;++i){d=a+b+c;a=b,b=c,c=d;//滚动操作}return d;}LeetCodeOJ练习
斐波那契数列模型
1.<面试题08.01> 三步问题
画图分析:

使用动态规划解决此题的步骤
1.创建dp表
2.确定状态表示
对于一般题都是集合经验和题目要求来确定
常见的经验有:以i位置为结尾xxx;以i位置为开始xxx 对于本题dp[i]表示到i位置的走法数
3.确定状态转移方程
确定方法一般为:以当前i位置状态最近的一步来划分问题,将划分的每个子问题用dp[x]表示

4.初始化,防止出现越界 对dp[1],dp[2],dp[3]进行初始化
5.填表顺序 从左往右
6.返回结果 dp[n]
具体代码:注意细节问题要将相加的结果模1e9+7,防止越界
int waysToStep(int n) {//1.创建dp表//2.初始化//3.填表//4.返回值const int MOD=1e9+7;//处理边界防止越界if(n==1 || n==2) return n;if(n==3) return 4;vector<int> dp(n+1);dp[1]=1,dp[2]=2,dp[3]=4;for(int i=4;i<=n;++i)dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;return dp[n];}2.LeetCode<746> 使用最小花费爬楼梯
画图分析:

使用动态规划解决此题的步骤:
1.创建dp表
2.确定状态表示
根据经验+题目要求,此处的dp[i]可以表示到达i位置时的最下花费
或者dp[i]表示从i位置开始到顶楼的最小花费
3.确定状态转移方程
(1)dp[i]可以表示到达i位置时的最下花费

对应代码
int minCostClimbingStairs(vector<int>& cost) {//1.创建dp表//2.初始化//3.填表//4.返回结果int n=cost.size();vector<int> dp(n+1);dp[0]=dp[1]=0;for(int i=2;i<=n;++i){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n];}(2) dp[i]表示从i位置开始到顶楼的最小花费

对应代码:
int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n);dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];for(int i=n-3;i>=0;--i)dp[i]=cost[i]+min(dp[i+1],dp[i+2]);return min(dp[0],dp[1]);}3.LeetCode<91> 解码方法
 使用动态规划解决此题的步骤
使用动态规划解决此题的步骤
1.创建dp表
2.确定状态表示
方法依旧是根据经验+结合题意
dp[i]表示以i位置为结尾,解析方法的总数(从开始解析到i位置的方法总数)
3.确定状态转移方程
根据最近的一步,划分问题
 具体代码为
具体代码为
int numDecodings(string s) {//1.创建dp表//2.初始化//3.填写dp表//4.返回结果int n = s.size();vector<int> dp(n); // 创建⼀个 dp表// 初始化前两个位置dp[0] = s[0] != '0';if(n == 1) return dp[0]; // 处理边界情况if(s[1]!='0') dp[1] += dp[0];int t = (s[0] - '0') * 10 + s[1] - '0';if(t >= 10 && t <= 26) dp[1] += 1;for(int i = 2; i < n; i++){// 如果单独编码if(s[i]!='0') dp[i] += dp[i - 1];// 如果和前⾯的⼀个数联合起来编码int t = (s[i - 1] - '0') * 10 + s[i] - '0';if(t >= 10 && t <= 26) dp[i] += dp[i - 2];}// 返回结果return dp[n - 1];}对于上述代码我们会发现初始化操作和填写表操作几乎一致,在这里我们就可以对边界问题和初始化问题做优化的
优化的方法为添加虚拟头结点,使新dp表和旧dp表产生如下的映射关系

这里有两个需要注意的问题
(1)虚拟节点里面的值,要确保后面的填表也是正确的
(2)新旧dp表下标间的映射关系
对于(1)的话,新的dp表中,对于计算dp[2]=dp[1]+dp[0],dp[1]是直接映射下来的不用管,重点是dp[0]中的值,当球dp[2]要用到dp[0]时,若原字符串中的第一个和第二个位置字符拼起来能解码成功时,说明s[0]也是可以单独解码成功的,若dp[0]=0的话,就会缺失这个能单独解码的情况,所以dp[0]=1
优化后的代码
int numDecodings(string s) {//1.创建dp表//2.初始化//3.填写dp表//4.返回结果int n = s.size();vector<int> dp(n+1); // 创建⼀个 dp表// 初始化前两个位置dp[0] = 1;dp[1]=s[1-1]!='0';for(int i = 2; i <= n; i++){// 如果单独编码if(s[i-1]!='0') dp[i] += dp[i - 1];// 如果和前⾯的⼀个数联合起来编码int t = (s[i - 2] - '0') * 10 + s[i-1] - '0';if(t >= 10 && t <= 26) dp[i] += dp[i - 2];}// 返回结果return dp[n];}相关文章:

动态规划<一>初识动态规划
目录 认识动态规划 LeetCodeOJ练习 斐波那契数列模型 认识动态规划 1.动态规划是一种用于解决优化问题的算法策略。 2.它的核心原理是把一个复杂的问题分解为一系列相互关联的子问题。通过先求解子问题,并且记录这些子问题的解(通常用一个表格之类的…...

【AIGC】ChatGPT提示词Prompt精确控制指南:Scott Guthrie的建议详解与普通用户实践解析
博客主页: [小ᶻZ࿆] 本文专栏: AIGC | ChatGPT 文章目录 💯前言💯斯科特古斯里(Scott Guthrie)的建议解读人机交互设计的重要性减轻用户认知负担提高Prompt的易用性结论 💯普通用户视角的分析普通用户…...

2024年10月24日随笔
1024程序员节啊,现在已经是晚上的十点半了,我还在实验室里没走,刚把力扣的每日一题写完,好忙啊,好忙啊,好忙啊,为什么都大三了我还不能做自己的事情,今天老师开会说要给互联网加大赛…...

怎么做系统性能优化
对于软件或系统的性能优化,可以采取多种措施来提高效率和响应速度。这里为您列举一些常见的方法: 1. 代码优化:检查并优化算法复杂度,减少不必要的计算。使用更高效的数据结构和算法。 2. 数据库优化: •索引优化&…...

负载均衡:四层与七层
负载均衡建立在现在网络基础之上,提供一种廉价透明有效的方式扩展网络设备和服务器带宽、增加吞吐量、加强网络数据处理能力、提高网络的灵活性和可用性。负载均衡可分为七层负载与四层负载。 四层负载(目标地址与端口交换) 主要通过报文中…...

【Ubuntu】服务器系统重装SSHxrdpcuda
本文作者: slience_me Ubuntu系统重装操作合集 文章目录 Ubuntu系统重装操作合集1.1 系统安装:1.2 安装openssh-server更新系统包安装OpenSSH服务器检查SSH服务的状态配置防火墙以允许SSH测试SSH连接配置SSH(可选) 1.3 安装远程连…...

ChatGPT的模型训练入门级使用教程
ChatGPT 是由 OpenAI 开发的一种自然语言生成模型,基于 Transformer 架构的深度学习技术,能够流畅地进行对话并生成有意义的文本内容。它被广泛应用于聊天机器人、客户服务、内容创作、编程助手等多个领域。很多人对如何训练一个类似 ChatGPT 的语言模型…...

【OS】2.1.2 进程的状态与转换_进程的组织
✨ Blog’s 主页: 白乐天_ξ( ✿>◡❛) 🌈 个人Motto:他强任他强,清风拂山冈! 🔥 所属专栏:C深入学习笔记 💫 欢迎来到我的学习笔记! 一、进程的状态 1.1.创建态 ……的…...

和为 n 的完全平方数的最少数量
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。 示…...

Hallo2 长视频和高分辨率的音频驱动的肖像图像动画 (数字人技术)
HALLO2: LONG-DURATION AND HIGH-RESOLUTION AUDIO-DRIVEN PORTRAIT IMAGE ANIMATION 论文:https://arxiv.org/abs/2410.07718 代码:https://github.com/fudan-generative-vision/hallo2 模型:https://huggingface.co/fudan-generative-ai/h…...

如何在Debian 8上使用Let‘s Encrypt保护Apache
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 本教程将向您展示如何在运行 Apache 作为 Web 服务器的 Debian 8 服务器上设置来自 Let’s Encrypt 的 TLS/SSL 证书。我们还将介…...

百科知识|选购指南
百科知识||选购指南 百科知识选购指南茶叶分类茶叶的味道来源茶叶制作步骤名茶其他一些茶叶的知识 百科知识 选购指南 茶叶 分类 茶叶种类: 六大茶类完美分析介绍!茶友推荐收藏 (aboxtik.com) 1.绿茶(发酵率0%) 2.白茶(发酵率…...

Go 语言基础教程:4.常量的使用
在这篇教程中,我们将通过一个简单的 Go 语言程序来学习常量的声明和使用。以下是我们要分析的代码: package mainimport ("fmt""math" )const s string "constant"func main() {fmt.Println(s)const n 500000000const …...

centos服务器重启后,jar包自启动
第一种方法: systemctl服务自启动 在/usr/lib/systemd/system目录下,创建service:start_jar.servie [Unit] DescriptionYour Java Application as a Service Afternetwork.target[Service] Userroot Typesimple ExecStart/usr/bin/java -j…...

华为云实战杂记
配置nginx服务器 首先我们拿到一台服务器时,并不知道系统是否存在Nginx我们可以在Linux命令行执行如下命令查看 find / -name nginx* find / -name nginx* 查找所有名字以nginx开头的文件或者目录,我们看看系统里面都有哪些文件先,这样可以快…...
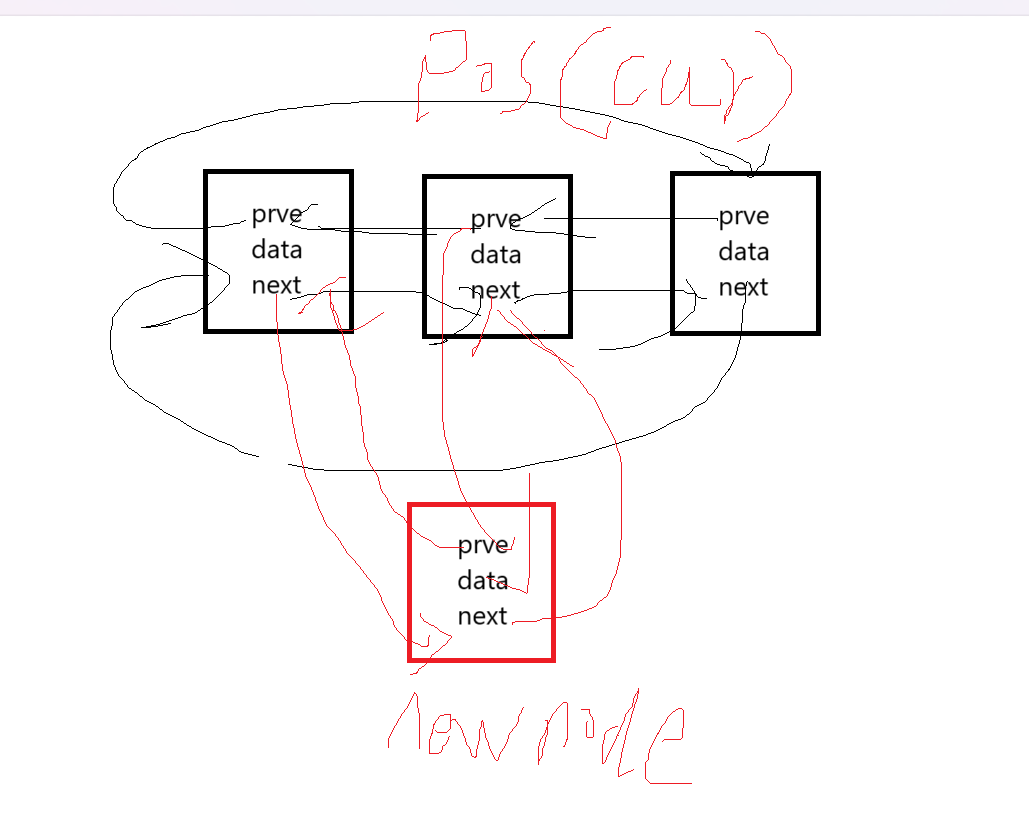
Lesson10---list
Lesson10—list 第10章 c的list的使用和实现 文章目录 Lesson10---list前言一、list的初始化二、list的遍历1.迭代器2.范围for 三、list常用的内置函数1.sort(慎用)2.unique3.reverse4.merge5.splice 四、模拟实现1.基本框架2.构造函数3.push_back4. 遍…...
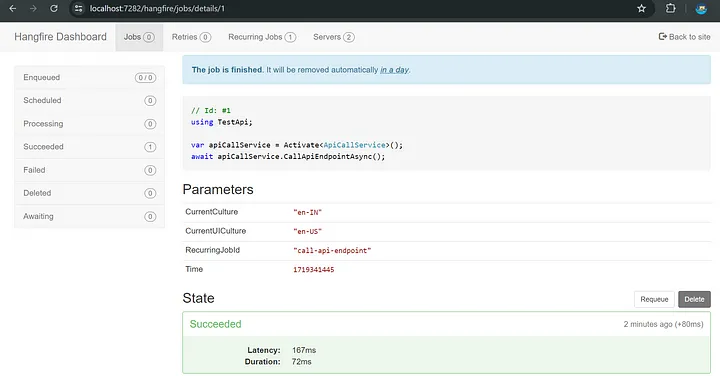
ASP.NET Core 8.0 中使用 Hangfire 调度 API
在这篇博文中,我们将引导您完成将 Hangfire 集成到 ASP.NET Core NET Core 项目中以安排 API 每天运行的步骤。Hangfire 是一个功能强大的库,可简化 .NET 应用程序中的后台作业处理,使其成为调度任务的绝佳选择。继续阅读以了解如何设置 Hang…...

查看linux的版本
在 Linux 系统中,有多种方法可以查看当前系统的版本信息。以下是一些常用的方法: 1. 使用 uname 命令 uname 命令可以显示系统的内核版本和其他相关信息。 uname -a这个命令会输出类似如下的信息: Linux hostname 5.4.0-88-generic #99-U…...

Mysql补充
单例 双重检查锁 class Singleton {private static volatile Singleton instance ;private Singleton() {}public static Singleton getInstance(){if(instance null) {synchronized (Singleto.class) {if(instance null){instance new Singleton() ;}} return instance;} …...

com.baomidou.mybatisplus.extension.service.IService用法详解及使用例子
IService 是 MyBatis-Plus 中的一个接口,提供了通用的 CRUD 操作,简化了数据库操作的代码。下面是 IService 的用法详解及示例代码。 1. 引入依赖 确保在你的 pom.xml 中添加了 MyBatis-Plus 的依赖: <dependency><groupId>co…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

第2课 SiC MOSFET与 Si IGBT 静态特性对比
2.1 输出特性对比 2.2 转移特性对比 2.1 输出特性对比 器件的输出特性描述了当温度和栅源电压(栅射电压)为某一具体数值时,漏极电流(集电极电流...

TMC2226超静音步进电机驱动控制模块
目前已经使用TMC2226量产超过20K,发现在静音方面做的还是很不错。 一、TMC2226管脚定义说明 二、原理图及下载地址 一、TMC2226管脚定义说明 引脚编号类型功能OB11电机线圈 B 输出 1BRB2线圈 B 的检测电阻连接端。将检测电阻靠近该引脚连接到地。使用内部检测电阻时,将此引…...

EC2安装WebRTC sdk-c环境、构建、编译
1、登录新的ec2实例,证书可以跟之前的实例用一个: ssh -v -i ~/Documents/cert/qa.pem ec2-user70.xxx.165.xxx 2、按照sdk-c demo中readme的描述开始安装环境: https://github.com/awslabs/amazon-kinesis-video-streams-webrtc-sdk-c 2…...

Python 解释器安装全攻略(适用于 Linux / Windows / macOS)
目录 一、Windows安装Python解释器1.1 下载并安装Python解释1.2 测试安装是否成功1.3 设置pip的国内镜像------永久配置 二、macOS安装Python解释器三、Linux下安装Python解释器3.1 Rocky8.10/Rocky9.5安装Python解释器3.2 Ubuntu2204/Ubuntu2404安装Python解释器3.3 设置pip的…...
