红黑树 学习笔记
目录
1.红黑树的概念
1.1红黑树的规则
1.2红黑树的效率
2.红黑树的实现
2.1红黑树的大致结构
2.2红黑树的插入
2.2.1红黑树插入的大致过程
2.2.2情况1:变色
2.2.3情况2:单旋+变色
2.2.4情况3:双旋+变色
2.3红黑树的查找
1.红黑树的概念
红黑树是一颗搜索二叉树,相比于搜索二叉树,红黑树中的每个节点增加了一个存储位置来表示节点的颜色,可以是红色或黑色。通过对于任何一条从根到叶子的路径上各个节点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因此红黑树也算比较平衡的树。
1.1红黑树的规则
1.每个节点不是红色就是黑色。
2.根节点是黑色的
3.如果一个节点是红色的,那么该节点的两个孩子节点必须为黑色,也就是说红黑树中,任何路径都不会包含连续的红色节点。
4.对于任意一个节点,从该节点到其所有的NULL节点的简单路径上,均包含相同数量的黑色节点。
例如:

1.2红黑树的效率
假设N是红黑树中的节点数量,h为红黑树中最短路径的长度,对于 - 1 <= N <
-1, 由此可推出,红黑树增删查改最坏的情况也就是走
,那么时间复杂度也就为 O(
)。
例如:

2.红黑树的实现
2.1红黑树的大致结构
enum COLOUR
{RED,BLACK
};//COLOUR 来控制每个节点的颜色template<class K, class V>
struct RBTreeNode
{pair<K, V> _value;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;COLOUR _col;// RED/BLACKRBTreeNode(const pair<K, V>& value):_value(value), _left(nullptr), _right(nullptr), _parent(nullptr),_col(RED) // 默认为红色,因为黑色会改变路径节点数量相等规则,较为麻烦{}
};template<class K, class V>
class RBTree
{using Node = RBTreeNode<K,V>;
public://... ...
private:Node* _root = nullptr;size_t num = 0;//记录节点数量
};2.2红黑树的插入
2.2.1红黑树插入的大致过程
- 插入一个新节点时,按照二叉搜索树的规则进行插入,插入之后我们只需要判断是否符合红黑树的4条规则。
- 如果是空树插入,新增加的节点为黑色节点(也就是根节点)。如果是非空树插入,新增节点必须为红色节点。因为插入黑色节点,对于红黑树的每条路径黑色节点数量均相同的规则,我们很难处理。
- 非空树插入后,新增节点必须是红色的,如果父节点为黑色,则不违反规则,插入结束。
- 非空树插入后,若父节点为红色节点,则违反规则,因为不能出现连续的红色节点。进一步分析为以下几种情况:
2.2.2情况1:变色

例如上述的一种情况,x节点是我们的新插入节点,很明显,x和6构成了连续的红色节点,并且此时的g为黑,u存在且为红。我们如果想要红黑树符合规则,必须将6的颜色变为黑色,但是在18->10->6->x这条路径上,就会多一个黑色节点,又会破坏规则。那么我们这么想:对于一个黑色节点,如果把该节点变为红色,同时把该节点的两个左右节点变为黑色,那么其实不会改变每一条路径上的黑色节点数量。例如:
我们将10变为红色,将6,15变为黑色。这样既满足了x与6不为连续的红色,也满足了每条路径上的黑色节点数量不变。
以上只是变色中的一种情况,同AVL树一样,如果我们将抽象图画出来,其实本质还是一样,不断往上变色,直到符合红黑树的规则即可。该情况的代码如下:
bool _Insert(const pair<K,V>& value)
{if (_root == nullptr){_root = new Node(value);_root->_col = BLACK;num++;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (value < cur->_value){parent = cur;cur = cur->_left;}else if (cur->_value < value){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(value);if (cur->_value < parent->_value){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent; //节点已经被插入,下面考察是否符合红黑树规则while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//找到父节点的父亲if (parent == grandfather->_left)//如果父亲在grandfather的左边{Node* uncle = grandfather->_right;//那么uncle就在grandfather右边if (uncle && uncle->_col == RED)//如果uncle存在并且为红色,一直往上变色即可{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}//... ...2.2.3情况2:单旋+变色
该情况下,肯定c和p为两个连续的红色节点,但此时g为黑,u不存在或者u存在且为黑。如果u存在且为黑,那么c一定不是新插入节点,否则就会所有路径黑色节点数量不同,如果u不存在,则c一定是新插入节点。
分析:和情况1一样,这里的p必须变为黑色,才能解决连续红色节点的问题,u不存在或者存在且为黑,这里单纯的变色就无法解决问题,因此我们需要旋转+变色。

对于上方左右两种情况,因为g为黑,因此我们进行单旋之后,g就会变成p的子树,此时我们把g变红,把p变黑即可解决问题。并且我们不需要继续向上更新,因为p已经变成这棵子树的根,且为黑色节点,一定不会和上方产生矛盾。

先看上方的图,如果c为新插入的节点,且u存在为黑,那么c左右都为空,红黑树规则就会被打破。所以c之前为黑,然后从下方子树一直往上变为红。
如果u不存在,那么c一定是新插入的节点。如果c不是新插入的节点,那么就说明插入之前就存在红黑树符合规则,所以c和p不连续为红,此时就不符合所有路径黑色节点数量相等,因为g的右边为空,所以假设不成立,c一定是新插入的节点。
然后我们再看旋转+变色之后的结果,都符合了红黑树的规则。左单旋与上面类似。
代码如下:
if (parent == grandfather->_left)
{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//情况1{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left)//情况2{RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;}else//情况3{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;break;}}
}2.2.4情况3:双旋+变色
情况3还是,c,p为红,g为黑,u不存在或者存在且为黑。u不存在,c一定是新增节点,u存在且为黑,c一定不是新增节点。

这里和情况2类似,我们只考虑左边的情况(右边逻辑类似):

我们学过AVL树都知道,尽管不变色,对于这种 < 类型的树,我们必须进行双旋,才能解决问题,< 进行 左右双旋,然后根据结果来看,我们只需要将c变为黑色,将p,g变为红色即可。
之后就是当p为g的右边,逻辑只是和上面的相反,这里就之间展示整个插入的代码:
bool _Insert(const pair<K,V>& value)
{if (_root == nullptr){_root = new Node(value);_root->_col = BLACK;num++;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (value < cur->_value){parent = cur;cur = cur->_left;}else if (cur->_value < value){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(value);if (cur->_value < parent->_value){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//插入完毕,准备检查是否为规则红黑树while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//如果p在g的左边{Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//u存在且为红,一直向上变色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//u不存在或者存在且为黑{if (cur == parent->_left)//c为p的左,右单旋+变色{RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;}else//c为p的右,左右双旋+变色{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;break;}}}// g// u p// c//else//p为g的右{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//u存在且为红,一直向上变色{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//u不存在或者存在且为黑{if (cur == parent->_right)//c为p的右,左单旋+变色{RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;}else//c为p的左,右左双旋+变色{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;break;}}}}_root->_col = BLACK;//无论如何,根节点都为黑色num++;//统计红黑树的节点数量return true;
}2.3红黑树的查找
红黑树的查找和AVL树类似,查找效率为O(),代码如下:
Node* find(const K& key)
{Node* cur = _root;while (cur){if (key < cur->_value.first){cur = cur->_left;}else if (key > cur->_value.first){cur = cur->_right;}else{return cur;}}return nullptr;
}以上内容若有错误,欢迎批评指正!
相关文章:
红黑树 学习笔记
目录 1.红黑树的概念 1.1红黑树的规则 1.2红黑树的效率 2.红黑树的实现 2.1红黑树的大致结构 2.2红黑树的插入 2.2.1红黑树插入的大致过程 2.2.2情况1:变色 2.2.3情况2:单旋+变色 2.2.4情况3:双旋变色 2.3红黑树的查找…...

linux更改系统时间
测试环境和生产环境代码完全一致,但是生产环境代码碰到了问题,报错类似time expired,猜测和系统时间有关系,修改之后确实好了。测试如下: 参考:centos7时间同步教程_centos7 时间同步,如果遇到…...
B站C#刘铁猛笔记
C#——刘铁猛笔记 类、名称空间(简述) 类(class)是构成程序的主体 名称空间(namespace)以树形结构组织类(其他类型) 名称空间:名称空间是用来组织和管理类、接口、结构…...

如何使用信号发生器产生正弦波并用数字示波器进行测量
使用信号发生器产生正弦波并用数字示波器进行测量的步骤如下: 1. 准备工作 所需设备 信号发生器数字示波器探头(通常为10X衰减探头)BNC电缆和适配器(如果需要) 2. 设置信号发生器 连接 使用BNC电缆将信号发生器的…...
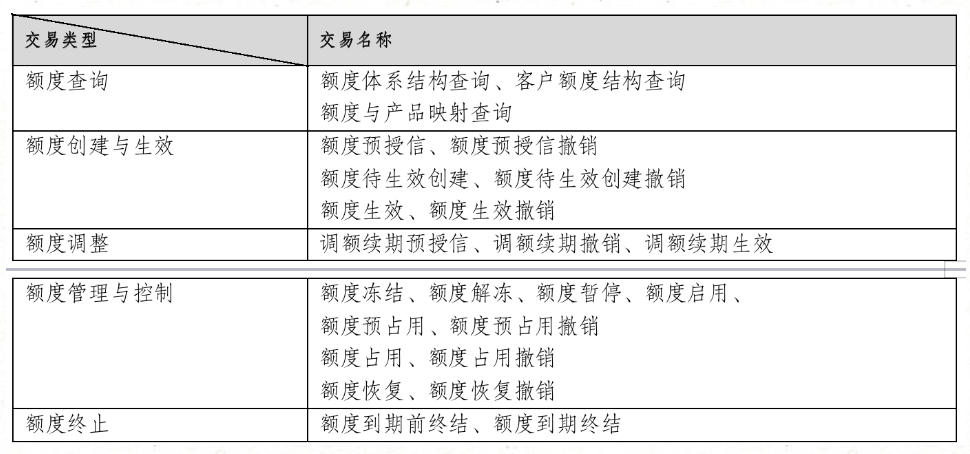
XJ04、消费金融|授信基本概念及其流程设计
银行是经营风险的特殊行业,而银行授信则与银行业务和风险天然相伴。它是银行与客户建立业务关系的起点,也是银行风险管理的关键环节和核心要素。若要了解银行业务,就得先了解银行的授信业务;若要理解银行经营,就得先理…...

儿童预防接种预约微信小程序springboot+论文源码调试讲解
2相关技术 2.1微信小程序 小程序是一种新的开放能力,开发者可以快速地开发一个小程序。小程序可以在微信内被便捷地获取和传播,同时具有出色的使用体验。尤其拥抱微信生态圈,让微信小程序更加的如虎添翼,发展迅猛。 2.2 MYSQL数据…...

nginx 修改配置
如果你的后端服务在不同的端口上运行,但静态资源访问路径相同,你可以使用 Nginx 的 location 配置来将请求转发到不同的后端服务,同时处理静态文件。这里有几种常见的方式: 方案 1: 基于路径的配置 如果所有服务的静态资源路径相…...

孤岛架构在安全性方面
孤岛架构在安全性方面的考虑主要涉及如何确保每个孤岛的安全性,同时维护整个系统的安全。 关键的安全性考虑: 1. 数据隔离和访问控制 数据隔离:每个孤岛应该有独立的数据存储,以确保数据隔离。这有助于防止数据泄露和未经授权的…...

COSCon'24 志愿者招募令:共创开源新生活!
亲爱的开源爱好者们, 第九届中国开源年会(COSCon24)即将在北京中关村国家自主创新示范区会议中心于2024年11月2日至3日隆重举行。今年的主题是“Open Source, Open Life|开源新生活”,旨在探索开源技术如何在各个领域推…...

vscode使用make编译c的问题
问题1:makefile:2: *** missing separator. Stop vscode的配置问题,看这哥们的文章即可:https://blog.csdn.net/m0_57464986/article/details/134220676 问题2:创建makefile文件 直接创建文件名为“makefile”的文件即可&#x…...

管家婆财贸ERP BB019.操作员制单日期控制
最低适用版本: 财贸系列 20.0 插件简要功能说明: 定制操作员权限功能,根据服务器日期控制系统单据新增和修改更多细节描述见下方详细文档 插件操作视频: 进销存类定制插件--操作员制单日期控制 插件详细功能文档: …...

从 Vue 2 到 Vue 3:全面升级指南
🌈个人主页:前端青山 🔥系列专栏:Vue篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来Vuet篇专栏内容:Vue-从 Vue 2 到 Vue 3:全面升级指南 前言 随着前端技术的不断发展,Vue.j…...

Apache paimon表操作实战-5
维表Join Paimon支持Lookup Join语法,它用于从 Paimon 查询的数据来补充维度字段。要求一个表具有处理时间属性,而另一个表由查找源连接器支持。 Paimon 支持 Flink 中具有主键的表和append-only的表查找联接。以下示例说明了此功能。 USE CATALOG fs_catalog; CREATE TABL…...

阿里云用STS上传oss的完整程序执行流程图 和前端需要哪些参数uniapp
H5 微信小程序可用的前端直传阿里云OSS(STS临时凭证前端签名)直接下载插件 下面是原理说明: 明白了,我来详细说明前端上传文件到阿里云OSS需要携带的具体参数: 从服务器获取的 STS 凭证: // 这些参数需要从你的后端服务器获…...

决策树方法根据指定条件筛选方案
代码功能说明 条件类:Condition 类用于定义每个条件的范围,并提供一个方法 is_satisfied 来检查输入值是否满足该条件。 算法选择器类:AlgorithmSelector 类负责应用条件并记录不满足的条件。它提供方法 apply_condition 用于更新可用算法&a…...

多特征变量序列预测(四) Transformer-BiLSTM风速预测模型
往期精彩内容: 时序预测:LSTM、ARIMA、Holt-Winters、SARIMA模型的分析与比较 全是干货 | 数据集、学习资料、建模资源分享! EMD、EEMD、FEEMD、CEEMD、CEEMDAN的区别、原理和Python实现(一)EMD-CSDN博客 EMD、EEM…...

【开源免费】基于SpringBoot+Vue.JS蜗牛兼职平台 (JAVA毕业设计)
本文项目编号 T 034 ,文末自助获取源码 \color{red}{T034,文末自助获取源码} T034,文末自助获取源码 目录 一、系统介绍1.1 平台架构1.2 管理后台1.3 用户网页端1.4 技术特点 二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景…...

Ajax笔记
介绍 Ajax是一种网页开发技术,全称是Asynchronous JavaScript and XML(异步JavaScript和XML)。作用如下: 数据交换:可以通过Ajax给服务器发送请求,并获取服务器响应的数据。即前端动态的发送Ajax到服务器端…...

软考:缓存分片和一致性哈希
缓存分片技术是一种将数据分散存储在多个节点上的方法,它在分布式缓存系统中尤为重要。这项技术的核心目的是提高系统的性能和可扩展性,同时确保数据的高可用性。以下是缓存分片技术的一些关键点: 数据分片:缓存分片涉及将数据分成…...

3109 体验积分值
经验值:1200 时间限制:1000毫秒 内存限制:128MB 合肥市第34届信息学竞赛(2017年) 不许抄袭,一旦发现,直接清空经验! 题目描述 Description 卡卡西和小朋友们做完了烧脑的数字游…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
