C语言巨难题:执行操作可获得的最大总奖励 I(C语言版)
1.题目:
给你一个整数数组 rewardValues,长度为 n,代表奖励的值。
最初,你的总奖励 x 为 0,所有下标都是 未标记 的。你可以执行以下操作 任意次 :
- 从区间
[0, n - 1]中选择一个 未标记 的下标i。 - 如果
rewardValues[i]大于 你当前的总奖励x,则将rewardValues[i]加到x上(即x = x + rewardValues[i]),并 标记 下标i。
以整数形式返回执行最优操作能够获得的 最大 总奖励。
示例 1:
输入:rewardValues = [1,1,3,3]
输出:4
解释:
依次标记下标 0 和 2,总奖励为 4,这是可获得的最大值。
示例 2:
输入:rewardValues = [1,6,4,3,2]
输出:11
解释:
依次标记下标 0、2 和 1。总奖励为 11,这是可获得的最大值。
提示:
1 <= rewardValues.length <= 5 * 1041 <= rewardValues[i] <= 5 * 104
该作者解决方法:
不知道C语言要怎么建构bitset,看了其他人的解答后尝试用位运速加速。 假设有一个 bool 数组 dp。在每一次循环中,dp[rewardValues[i] + j] 可以由 dp[j] 转移而来,其中 j 为小于 rewardValues[i] 的非负整数。 为了加速运算并减少空间浪费,可以将 bool 数组改成 unsigned long long。 在C语言中,虽 bool 使用1bit,但最小寻址单位为1字节,所以占用1字节。 现在我们将数组声明成 unsigned long long,此时每次操作最多可以操作64个位元,也就是64个状态。 由于 rewardValues[i] 不一定为64的倍数,为了避免发生溢位的状况,必须将 dp[j] 所代表的64位元拆成两部分。 为了计算正确的下标,我们把 rewardValues[i] 用 index 与 digit 表示,其中 rewardValues[i] = 64 * index + digit:
index = rewardValues[i] / 64
digit = rewardValues[i] % 64
因此,对于每个下标 j,dp[j] 可拆成:
(dp[j] & ((1 << (64 - digit)) - 1)) << digit
dp[j] >> (64 - digit)
假设 rewardValues[i] = 65,那么:
index = 65 / 64 = 1
digit = 65 % 64 = 1
以 dp[0] 的 0 ~ 63 位为例,0 ~ 62 位可以移到 dp[index + 0] 中的 1 ~ 63 位,对应数字 65 ~ 127。而剩下的1个位则放入 dp[index + 1] 的第 0 位,这个过程通过或运算即可。
dp[index + j] |= (dp[j] & ((1 << (64 - digit)) - 1)) << digit;
dp[index + j + 1] |= dp[j] >> (64 - digit);
若 rewardValues[i] 为 64 的倍数可直接转移,不需拆分
代码:
int cmp(const void *a, const void *b)
{return *(int*)a > *(int*)b;
}int maxTotalReward(int* rewardValues, int rewardValuesSize)
{qsort(rewardValues, rewardValuesSize, sizeof(int), cmp);int size = rewardValues[rewardValuesSize - 1] / 32 + 2;unsigned long long dp[size], temp, mask;memset(dp, 0, sizeof(unsigned long long) * size);int index, digit;dp[0] = 1;for (int i = 0; i < rewardValuesSize; ++i) {index = rewardValues[i] / 64;digit = rewardValues[i] % 64;mask = digit ? (1ULL << (64 - digit)) - 1 : 0;for (int j = 0; j < index; ++j){if (digit) {dp[j + index] |= (dp[j] & mask) << digit;dp[j + index + 1] |= dp[j] >> (64 - digit);} else {dp[j + index] |= dp[j];}}if (digit) {temp = dp[index] & ((1ULL << digit) - 1);dp[2 * index] |= (temp & mask) << digit;dp[2 * index + 1] |= temp >> 64 - digit;}}for (int i = size - 1; i >= 0; --i) {if (dp[i])return 64 * i + 63 - __builtin_clzll(dp[i]);}return 0;
}
声明:来源力扣题解
作者:borane
链接:https://leetcode.cn/problems/maximum-total-reward-using-operations-ii/solutions/2805771/01bei-bao-wei-yun-suan-by-modest-nashdn2-svmq/
来源:力扣(LeetCode)
相关文章:
)
C语言巨难题:执行操作可获得的最大总奖励 I(C语言版)
1.题目: 给你一个整数数组 rewardValues,长度为 n,代表奖励的值。 最初,你的总奖励 x 为 0,所有下标都是 未标记 的。你可以执行以下操作 任意次 : 从区间 [0, n - 1] 中选择一个 未标记 的下标 i。如果…...

【力扣】GO解决子序列相关问题
文章目录 一、引言二、动态规划方法论深度提炼子序列问题的通用解法模式 三、通用方法论应用示例:最长递增子序列(LeetCode题目300)Go 语言代码实现 四、最长连续递增序列(LeetCode题目674)Go 语言代码实现 五、最长重…...

Ubuntu20.04安装VM tools并实现主机和虚拟机之间文件夹共享
1、Ubuntu20.04安装VM tools 参考这个,很详细:Ubuntu 20.04 安装 VMwareTools 教程 2、实现主机与VMware虚拟机共享文件夹 设置共享文件夹参考:windows和虚拟机互传文件的三种方式 挂载操作参考:主机与VMware虚拟机共享文件夹&…...
—— 文件系统)
Linux 学习笔记(十七)—— 文件系统
终极目标:理解 inode 和 软硬连接; 文件系统:Ext2; 文件 文件内容 文件属性; ——> 磁盘上存储的文件 存储的文件内容 存储的文件属性; Linux系统中:文件内容使用数据块存储,文件属性使用inode(固定…...
)
【计算机网络 - 基础问题】每日 3 题(五十八)
✍个人博客:https://blog.csdn.net/Newin2020?typeblog 📣专栏地址:http://t.csdnimg.cn/fYaBd 📚专栏简介:在这个专栏中,我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞…...

Netty入门基础:IO模型中BIO\NIO概念及区别【附演示代码】
文章目录 😀BIO💢实战demo 🌈NIO🏍Buffer核心属性核心方法 🎗Channel🎈Selector核心方法 🧨实战demo 🎨粘包与半包 😀BIO 传统IO模型,同步阻塞,每…...

vue2 使用环境变量
一. 在根目录下创建.env.xxx文件 .env 基础系统变量,无论何种环境,都可使用其中配置的值,其他环境中的变量会覆盖.env中的同名变量。 .env.development 开发环境 .env.production 生产环境 .env.staging 测试环境 二. 内容格式 vue2 使用是以…...

数据预处理
继续提取代码片段: 12. **导入iris数据集并查看前5行数据**: python from sklearn.datasets import load_iris iris load_iris() X iris.data print(iris数据集的维度为:, X.shape) print(iris数据集的前5行数据为:\n, X[:5]) …...

django宠物领养管理系统-计算机毕业设计源码26858
目录 1 绪论 1.1 选题背景与意义 1.2国内外研究现状 1.3论文结构与章节安排 2系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据流程 3.3.2 业务流程 2.3 系统功能分析 2.3.1 功能性分析 2.3.2 非功能性分析 2.4 系统用例分析 2.5本章小结 3 系统总体设计 3…...

使用TeamViewer远程局域网内的两台电脑
有个场景,有人还不知道TV可以局域网操作,记录一下。 主要就是修改设置,将取消激活改为接受 然后输入受控端的ip即可...

GUI简介、Swing的常用组件、java程序的运行过程、class文件、JAR、runable_jar、双括号初始化
GUI简介 GUI:图形用户界面,在计算机中采用图形的方式显示用户界面 java的GUI开发 AWT:java最早推出的GUI编程开发包,界面风格跟随操作系统SWT:eclipse就是java使用SWT开发的Swing:在AWT的基础上扩充了功能…...
区别)
@Autowired和@Resource和getBean()区别
今天遇到一个对我来说很奇葩的错误,我想在Service中注入bean,我这里使用了Autowired和Resource都不能注入,导致初始化失败,使用了getBean()方法就可以注入。从来没有遇到过这个问题。后来我查询了一下,才明白了原理。我…...
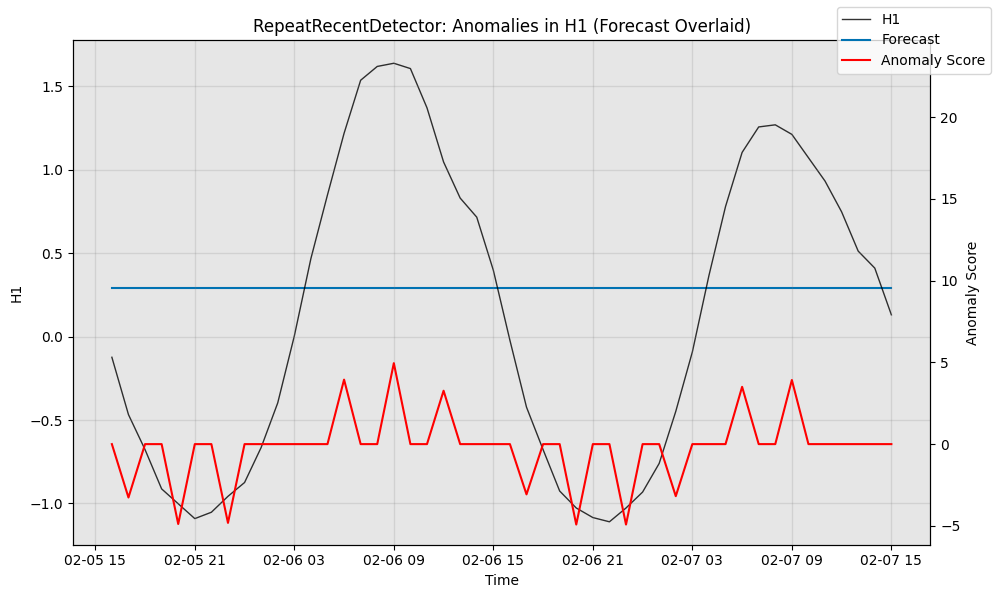
Merlion笔记(四):添加一个新的预测模型
文章目录 1 模型配置类2 模型类3 运行模型:一个简单的例子4 可视化5 定量评估6 定义一个基于预测器的异常检测器 本文提供了一个示例,展示如何向 Merlion 添加一个新的预测模型,遵循 CONTRIBUTING.md 中的说明。建议在阅读本篇文章之前,先查…...

【论文阅读】ESRGAN
学习资料 论文题目:增强型超分辨率生成对抗网络(ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks)论文地址:[1809.00219] ESRGAN:增强型超分辨率生成对抗网络代码:xinntao / ESRGAN&am…...

电脑异常情况总结
文章目录 笔记本无症状息屏黑屏 笔记本无症状息屏黑屏 🍎 问题描述: 息屏导致黑屏;依次操作计算机--》右键--》管理--》事件查看器--》Windows日志--》系统;从息屏到异常黑屏之间出现了很多错误,如下:事件…...

[项目详解][boost搜索引擎#1] 概述 | 去标签 | 数据清洗 | scp
目录 一、前言 二、项目的相关背景 三、搜索引擎的宏观原理 四、搜索引擎技术栈和项目环境 五、正排索引 VS 倒排索引--原理 正排索引 分词 倒排索引 六、编写数据去除标签和数据清洗模块 Parser 1.数据准备 parser 编码 1.枚举文件 EnumFile 2.去标签ParseHtml(…...

PL/I语言的起源?有C语言,有B语言和A语言吗?为什么shell脚本最开始可能有#!/bin/bash字样?为什么不支持嵌套注释?
PL/I语言的起源 在20世纪50~60年代,当时主流的编程语言是COBOL/FORTRAN/ALGOL等,IBM想要设计一门通用的编程语言,已有的编程语言无法实现此要求,故想要设计一门新语言,即是PL/I. PL/I是Programming Language/One的缩写…...

gin入门教程(3):创建第一个 HTTP 服务器
首先设置golang github代理,可解决拉取git包的时候,无法拉取的问题: export GOPROXYhttps://goproxy.io再查看自己的go版本: go version我这里的版本是:go1.23.2 linux/arm64 准备工作做好之后就可以进行开发了 3.…...

Vue+ECharts+iView实现大数据可视化大屏模板
Vue数据可视化 三个大屏模板 样式还是比较全的 包括世界地图、中国地图、canvas转盘等 项目演示: 视频: vue大数据可视化大屏模板...

el-table 表格设置必填项
el-table 表格设置必填项 要在 el-table 中集成 el-form 来设置必填项,并进行表单验证,可以使用 Element UI 提供的表单验证功能。下面是一个详细的示例,展示了如何在 el-table 中使用 el-form 来设置必填项,并进行验证。 示例代…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
