LeetCode - 4. 寻找两个正序数组的中位数
. - 力扣(LeetCode)
题目
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
- 示例 1:
- 输入:nums1 = [1,3], nums2 = [2]
- 输出:2.00000
- 解释:合并数组 = [1,2,3] ,中位数 2
- 示例 2:
- 输入:nums1 = [1,2], nums2 = [3,4]
- 输出:2.50000
- 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000
解题方案
首先明确中位数的位置
1. 暴力解法(合并数组)
合并成一个新数组,然后sort,取中位数。
- 边界情况:合并后数组的长度为0,则无中位数
- 合并数组(nums)长度为偶数(n),则中位数为第
位和第
位的平均值,即
- 合并数组(nums)长度为奇数(n), 则中位数为第
位,即
接下来,人生苦短,我用Python~
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:# 合并数组并排序nums1.extend(nums2)nums1.sort()length = len(nums1)if length < 1:return Noneif length % 2 == 0:return (nums1[length // 2 - 1] + nums1[length // 2]) / 2else:return nums1[length // 2]分析时空复杂度
- 记nums1长度为m, nums2长度为n
- 合并数组时间复杂度是
,空间复杂度是
- 数组排序时间复杂度是
,空间复杂度是
故总的时间复杂度是,空间复杂度是
虽然看上去代码非常精炼,但是从时空复杂度上看,算法并不好,毕竟题目中"正序(从小到大)数组"这个条件没有用到。因此考虑有序归并
2. 暴力解法优化版(有序合并数组)
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:m = len(nums1)n = len(nums2)# 合并数组nums = []if m == 0:nums = nums2elif n == 0:nums = nums1else:index_1 = 0index_2 = 0while True:if index_1 >= m and index_2 >= n:breakelif index_2 >= n or (index_1 < m and nums1[index_1] <= nums2[index_2]):nums.append(nums1[index_1])index_1 += 1elif index_1 >=m or (index_2 < n and nums1[index_1] > nums2[index_2]):nums.append(nums2[index_2])index_2 += 1total_length = len(nums)if total_length < 1:return Noneelif total_length % 2 == 0:return (nums[total_length // 2 - 1] + nums[total_length // 2]) / 2else:return nums[total_length // 2]分析时空复杂度
- 时间复杂度为合并数组花费的时间,
- 空间复杂度为合并后数组的空间,
(如果不存储合并的数组,空间复杂度可以做到O(1))
题目给出的条件都用上了,时空复杂度也得到了提升,但仍然不符合题目要求的 O(log (m+n))的时间复杂度,需要进一步优化。
有序数组寻找中位数,考虑二分法。
3. 二分法
考虑一个长度为n有序数组的中位数,其中位数:
- 如果n为奇数,则中位数为第
大的数。
- 如果n为偶数,则中位数为第
大的数和第
大的数的平均值。
因此,中位数问题可以转换为另一个问题,寻找数组中第k小的数
(对于长度为偶数的情况,需要寻找两次,并取平均值)
class Solution:def getKthNumber(self, nums1: List[int], nums2: List[int], k: int) -> int:"""寻找两个正序整数数组中,第k小的数"""passdef findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:"""中位数计算入口函数"""total_length = len(num1) + len(nums2)if total_length < 1:return Noneelif total_length % 2 == 0:return (self.getKthNumber(nums1, nums2, total_length // 2) + self.getKthNumber(nums1, nums2, total_length // 2 + 1)) / 2else:return self.getKthNumber(num1, nums2, total_length // 2 + 1)接着看如何寻找两个正序数组中第k小的数:
- 如果时间复杂度是
O(log (m+n)),考虑用二分法。
先看下面这个例子:


由此,我们可以总结我们两个正序数组中,寻找第k小的数的思路:
1. 如果k=1, 则首先比较两个数组首位元素,取最小的一个。
2. 如果k>1, 则比较两个数组中第
个元素,较小的一个数组中的第1~
个元素一定是小于我们目标值的,因此可以排除这一段(如上图中灰色部分),在剩余元素中继续寻找第(
)小的元素。
3. 如果某个数组完全被排除掉了,则直接在剩余的另一个数组中定位目标元素即可。如下面的例子:
class Solution:def getKthNumber(self, nums1: List[int], nums2: List[int], k: int) -> int:"""寻找两个正序整数数组中,第k大的数"""# 记录数组长度m = len(nums1)n = len(nums2)# 记录数组可以查找的起始位置索引index_1 = 0index_2 = 0while True:# 极端情况1 - nums1已经被排除为空if index_1 >= m:return nums2[index_2 + k - 1]# 极端情况2 - nums2已经被排除为空if index_2 >= n:return nums1[index_1 + k - 1]# 极端情况3 - 寻找最小的数if k == 1:return min(nums1[index_1], nums2[index_2])# 正常情况, 二分查找new_index_1 = min(k // 2 - 1 + index_1, m - 1)new_index_2 = min(k // 2 - 1 + index_2, n - 1)if nums1[new_index_1] <= nums2[new_index_2]:k -= (new_index_1 - index_1 + 1)index_1 = new_index_1 + 1else:k -= (new_index_2 - index_2 + 1)index_2 = new_index_2 + 1def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:"""寻找中位数 入口函数"""total_length = len(nums1) + len(nums2)if total_length < 1:return Noneelif total_length % 2 == 0:return (self.getKthNumber(nums1, nums2, total_length // 2) + self.getKthNumber(nums1, nums2, total_length // 2 + 1)) / 2else:return self.getKthNumber(nums1, nums2, total_length // 2 + 1)分析时空复杂度
-
时间复杂度
-
空间复杂度
AI会怎么做?
智谱清言给出了一种更高效的解法,划分数组二分法。
思路:
- 对一个长度为n的数组,从任意位置i将数组划分为两部分,可以有n+1种分发(
),如图所示,4个元素的数组,有4+1=5种划分方法。
- 中位数的作用是什么呢?将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。
- 对数组A从i位置进行划分,对数组B在j位置划分,数组A的左半部分和数组B的左半部分合起来叫做left_part, 数组A的有半部分和数组B的右半部分合起来叫做right_part, 则中位数是这样的一种划分:
- 对于两个数组长度之和为偶数的情况:
,中位数为
,此时划分位置满足
- 对于两个数组长度之和为奇数的情况:
,中位数为
,此时划分位置满足
- 合并上述两种,可以知道中位数情况下的划分:
- 如果我们保证
(避免j计算出负数), 可以导出:
- 通过上述推导,中位数问题可以转换为:寻找
,使得:
且
,其中
,
- 进一步简化为:在
中寻找最大的
,使得
,其中
。接下来就可以在
上对
进行二分查找了。
如此复杂的推导过程,又是担心被AI取代的一天。。。
def findMedianSortedArrays(nums1, nums2):# 确保 nums1 是较短的数组if len(nums1) > len(nums2):nums1, nums2 = nums2, nums1m, n = len(nums1), len(nums2)imin, imax, half_len = 0, m, (m + n + 1) // 2while imin <= imax:i = (imin + imax) // 2j = half_len - iif i < m and nums1[i] < nums2[j - 1]:# i 需要增大imin = i + 1elif i > 0 and nums1[i - 1] > nums2[j]:# i 需要减小imax = i - 1else:# 找到合适的 i 和 jmax_of_left = 0if i == 0: max_of_left = nums2[j - 1]elif j == 0: max_of_left = nums1[i - 1]else: max_of_left = max(nums1[i - 1], nums2[j - 1])if (m + n) % 2 == 1:return max_of_leftmin_of_right = 0if i == m: min_of_right = nums2[j]elif j == n: min_of_right = nums1[i]else: min_of_right = min(nums1[i], nums2[j])return (max_of_left + min_of_right) / 2.0# 示例
print(findMedianSortedArrays([1, 3], [2])) # 输出: 2.0
print(findMedianSortedArrays([1, 2], [3, 4])) # 输出: 2.5
相关文章:
LeetCode - 4. 寻找两个正序数组的中位数
. - 力扣(LeetCode) 题目 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 示例 1: 输入:nums1 …...
算法设计与分析——动态规划
1.动态规划基础 1.1动态规划的基本思想 动态规划建立在最优原则的基础上,在每一步决策上列出可能的局部解,按某些条件舍弃不能得到最优解的局部解,通过逐层筛选减少计算量。每一步都经过筛选,以每一步的最优性来保证全局的最优性…...

【实战篇】GEO是什么?还可以定义新的数据类型吗?
背景 之前,我们学习了 Redis 的 5 大基本数据类型:String、List、Hash、Set 和 Sorted Set,它们可以满足大多数的数据存储需求,但是在面对海量数据统计时,它们的内存开销很大,而且对于一些特殊的场景&…...
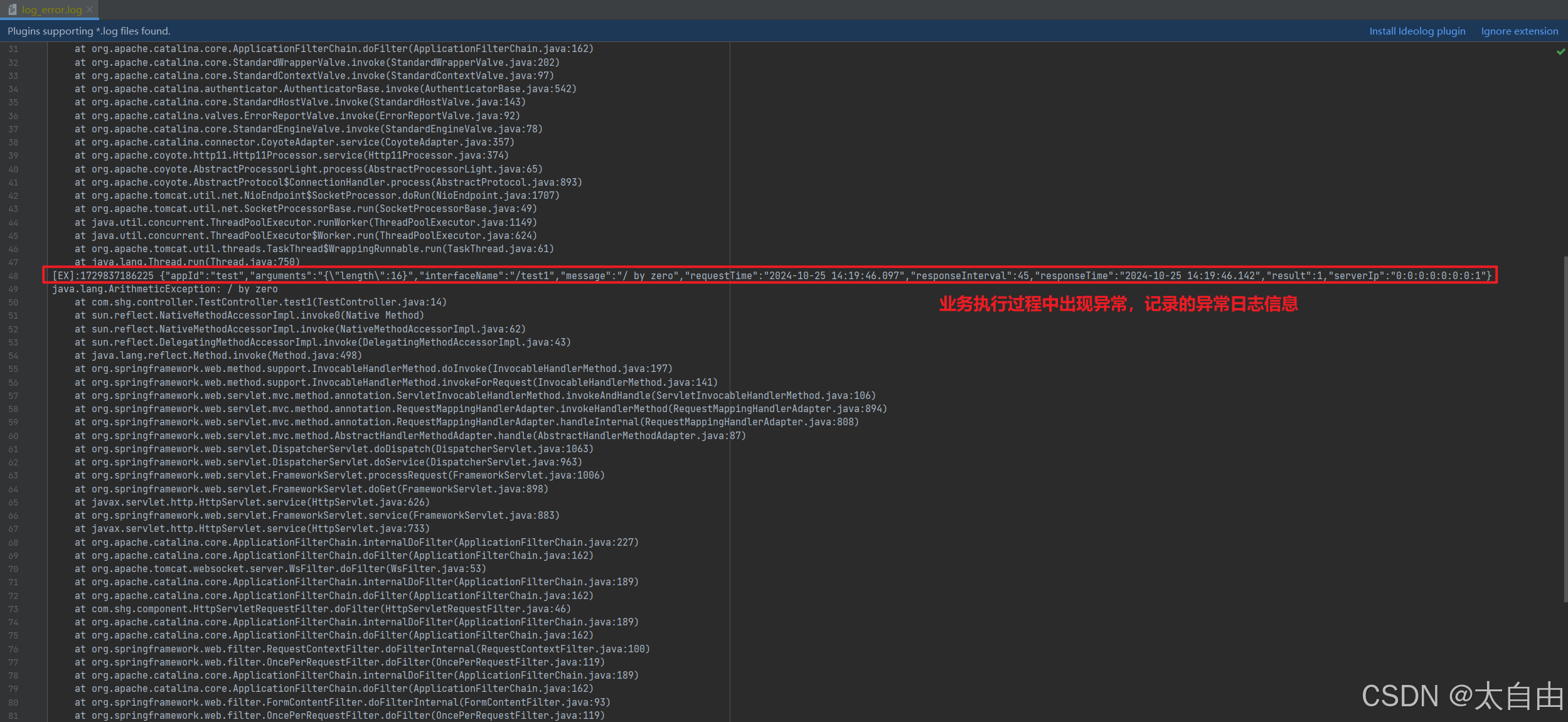
SpringBoot最佳实践之 - 项目中统一记录正常和异常日志
1. 前言 此篇博客是本人在实际项目开发工作中的一些总结和感悟。是在特定需求背景下,针对项目中统一记录日志(包括正常和错误日志)需求的实现方式之一,并不是普适的记录日志的解决方案。所以阅读本篇博客的朋友,可以参考此篇博客中记录日志的…...
)
【Flutter】状态管理:高级状态管理 (Riverpod, BLoC)
当项目变得更加复杂时,简单的状态管理方式(如 setState() 或 Provider)可能不足以有效地处理应用中状态的变化和业务逻辑的管理。在这种情况下,高级状态管理框架,如 Riverpod 和 BLoC,可以提供更强大的工具…...

OAK相机的RGB-D彩色相机去畸变做对齐
▌低畸变标准镜头的OAK相机RGB-D对齐的方法 OAK相机内置的RGB-D管道会自动将深度图和RGB图对齐。其思想是将深度图像中的每个像素与彩色图像中对应的相应像素对齐。产生的RGB-D图像可以用于OAK内置的图像识别模型将识别到的2D物体自动映射到三维空间中去,或者产生的…...

smartctl硬盘检查工具
一、smartctl工具简介 Smartmontools是一种硬盘检测工具,通过控制和管理硬盘的SMART(Self Monitoring Analysis and Reporting Technology),自动检测分析及报告技术)技术来实现的,SMART技术可以对硬盘的磁头单元、盘片电机驱动系统、硬盘…...

清空MySQL数据表
要清空 MySQL 数据表,您可以使用 TRUNCATE 或 DELETE 命令 使用 TRUNCATE 命令 TRUNCATE 命令用于删除表中的所有数据,并重置自增 ID(如果存在): TRUNCATE TABLE table_name;将 table_name 替换为您要清空的表的名称…...

2024年妈杯MathorCup大数据竞赛A题超详细解题思路
2024年妈杯大数据竞赛初赛整体难度约为0.6个国赛。A题为台风中心路径相关问题,为评价预测问题;B题为库存和销量的预测优化问题。B题难度稍大于A题,可以根据自己队伍情况进行选择。26日早六点之前发布AB两题相关解题代码论文。 下面为大家带来…...

Kafka系列之:Kafka集群磁盘条带划分和Kafka集群磁盘扩容详细方案
Kafka系列之:Kafka集群磁盘条带划分和Kafka集群磁盘扩容详细方案 一、lsblk命令二、Kafka节点磁盘条带化方案一三、Kafka节点磁盘条带化方案二四、理解逻辑区块LE五、查看kafka节点磁盘条带划分情况六、Kafka节点磁盘扩容一、lsblk命令 lsblk命令用于列出块设备的信息,包括磁…...

【LeetCode】修炼之路-0007- Reverse Integer (整数反转)【python】
题目 Reverse Integer Given a signed 32-bit integer x, return x with its digits reversed. If reversing x causes the value to go outside the signed 32-bit integer range [-231, 231 - 1], then return 0. Assume the environment does not allow you to store 64-b…...
)
【Flutter】页面布局:线性布局(Row 和 Column)
在 Flutter 中,布局(Layout)是应用开发的核心之一。通过布局组件,开发者可以定义应用中的控件如何在屏幕上排列。Row 和 Column 是 Flutter 中最常用的两种线性布局方式,用于水平和垂直排列子组件。在本教程中…...
)
C语言巨难题:执行操作可获得的最大总奖励 I(C语言版)
1.题目: 给你一个整数数组 rewardValues,长度为 n,代表奖励的值。 最初,你的总奖励 x 为 0,所有下标都是 未标记 的。你可以执行以下操作 任意次 : 从区间 [0, n - 1] 中选择一个 未标记 的下标 i。如果…...

【力扣】GO解决子序列相关问题
文章目录 一、引言二、动态规划方法论深度提炼子序列问题的通用解法模式 三、通用方法论应用示例:最长递增子序列(LeetCode题目300)Go 语言代码实现 四、最长连续递增序列(LeetCode题目674)Go 语言代码实现 五、最长重…...

Ubuntu20.04安装VM tools并实现主机和虚拟机之间文件夹共享
1、Ubuntu20.04安装VM tools 参考这个,很详细:Ubuntu 20.04 安装 VMwareTools 教程 2、实现主机与VMware虚拟机共享文件夹 设置共享文件夹参考:windows和虚拟机互传文件的三种方式 挂载操作参考:主机与VMware虚拟机共享文件夹&…...
—— 文件系统)
Linux 学习笔记(十七)—— 文件系统
终极目标:理解 inode 和 软硬连接; 文件系统:Ext2; 文件 文件内容 文件属性; ——> 磁盘上存储的文件 存储的文件内容 存储的文件属性; Linux系统中:文件内容使用数据块存储,文件属性使用inode(固定…...
)
【计算机网络 - 基础问题】每日 3 题(五十八)
✍个人博客:https://blog.csdn.net/Newin2020?typeblog 📣专栏地址:http://t.csdnimg.cn/fYaBd 📚专栏简介:在这个专栏中,我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞…...

Netty入门基础:IO模型中BIO\NIO概念及区别【附演示代码】
文章目录 😀BIO💢实战demo 🌈NIO🏍Buffer核心属性核心方法 🎗Channel🎈Selector核心方法 🧨实战demo 🎨粘包与半包 😀BIO 传统IO模型,同步阻塞,每…...

vue2 使用环境变量
一. 在根目录下创建.env.xxx文件 .env 基础系统变量,无论何种环境,都可使用其中配置的值,其他环境中的变量会覆盖.env中的同名变量。 .env.development 开发环境 .env.production 生产环境 .env.staging 测试环境 二. 内容格式 vue2 使用是以…...

数据预处理
继续提取代码片段: 12. **导入iris数据集并查看前5行数据**: python from sklearn.datasets import load_iris iris load_iris() X iris.data print(iris数据集的维度为:, X.shape) print(iris数据集的前5行数据为:\n, X[:5]) …...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...


