codeforces _ 补题
C. Ball in Berland
传送门:Problem - C - Codeforces
题意:

思路:容斥原理
考虑 第 i 对情侣组合 ,男生为 a ,女生为 b ,那么考虑与之匹配的情侣 必须没有 a | b
,一共有 k 对情侣, a | b 可以表示为 k - cnt[a] - cnt[b] + 1 ( cnt[a] 表示为有男生 a 的方案数 )
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{int n , m , k; cin >> n >> m >> k;vector<int> cnta( n + 1 ) , cntb( m + 1 ) , a( k + 1 ) , b( k + 1 );for( int i = 1 ; i <= k ; i++ ) cin >> a[i] , cnta[a[i]]++;for( int i = 1 ; i <= k ; i++ ) cin >> b[i] , cntb[b[i]]++;int ans = 0;for( int i = 1 ; i <= k ; i++ ){ans += k - cnta[a[i]] - cntb[b[i]] + 1;}cout << ans / 2 << endl;
}
signed main()
{int tt; cin >> tt;while(tt--)solve();return 0;
}B. Sifid and Strange Subsequences
传送门:Problem - B - Codeforces
题意:

思路:
我们要保证 | a[i] - a[j] | 的最小值 要 >= MAX ( MAX为 a[i] 中的某一个值 )
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{int n; cin >> n;vector<int> a(n + 1);for( int i = 1 ; i <= n ; i++ ) cin >> a[i];int cnt = 0; sort( a.begin() + 1 , a.end() );for( int i = 1 ; i <= n ; i++ )if( a[i] <= 0 )cnt++; // 此时的 cnt 表示 a[i] <= 0 的个数int mn = 2e18;for( int i = 1 ; i < cnt ; i++ )mn = min( mn , a[i + 1] - a[i] );for( int i = cnt + 1 ; i <= n ; i++ ){// 考虑 a[i] > 0 的情况mn = min( mn , a[i] - a[i-1] );if( mn >= a[i] )cnt++;else break;}cout << cnt << endl;
}
signed main()
{int tt; cin >> tt;while(tt--)solve();return 0;
}传送门:Problem - A - Codeforces
A. Bestie
题意:

思路:
首先有一个结论 gcd( n , n - 1 ) == 1
所以这个题的答案一定 <= 3
分情况讨论即可 答案为 1 2 3时的情况
#include<bits/stdc++.h>
using namespace std;
#define int long long
int gcd( int a , int b )
{return b ? gcd( b , a % b ) : a;
}
void solve()
{int n; cin >> n;vector<int> a( n + 1 );for( int i = 1 ; i <= n ; i++ ) cin >> a[i];int g = 0;for( int i = 1 ; i <= n ; i++ )g = gcd( g , a[i] );int temp1 = 0 ;for( int i = 1 ; i <= n; i++ )temp1 = gcd( temp1 , a[i] );int temp2 = 0;for( int i = 1 ; i <= n ; i++ ){if( i == n - 1 )continue;temp2 = gcd( temp2 , a[i] );}if( g == 1 ){cout << 0 << endl;}else if( gcd( temp1 , gcd( n , a[n] ) ) == 1 ){cout << 1 << endl;}else if( gcd( temp2 , gcd( n - 1 , a[n - 1] ) ) == 1 ){cout << 2 << endl;}else cout << 3 << endl;
}
signed main()
{int tt; cin >> tt;while(tt--)solve();return 0;
}相关文章:

codeforces _ 补题
C. Ball in Berland 传送门:Problem - C - Codeforces 题意: 思路:容斥原理 考虑 第 i 对情侣组合 ,男生为 a ,女生为 b ,那么考虑与之匹配的情侣 必须没有 a | b ,一共有 k 对情侣&#x…...

DataSophon集成ApacheImpala的过程
注意: 本次安装操作系统环境为Anolis8.9(Centos7和Centos8应该也一样) DataSophon版本为DDP-1.2.1 整合的安装包我放网盘了: 通过网盘分享的文件:impala-4.4.1.tar.gz等2个文件 链接: https://pan.baidu.com/s/18KfkO_BEFa5gVcc16I-Yew?pwdza4k 提取码: za4k 1…...

深入探讨TCP/IP协议基础
在当今数字化的时代,计算机网络已经成为人们生活和工作中不可或缺的一部分。而 TCP/IP 协议作为计算机网络的核心协议,更是支撑着全球互联网的运行。本文将深入探讨常见的 TCP/IP 协议基础,带你了解计算机网络的奥秘。 一、计算机网络概述 计…...

《Windows PE》7.4 资源表应用
本节我们将通过两个示例程序,演示对PE文件内图标资源的置换与提取。 本节必须掌握的知识点: 更改图标 提取图标资源 7.4.1 更改图标 让我们来做一个实验,替换PE文件中现有的图标。如果手工替换,一定是先找到资源表,…...

【重生之我要苦学C语言】猜数字游戏和关机程序的整合
今天来把学过的猜数字游戏和关机程序来整合一下 如果有不明白的可以看往期的博客 废话不多说,上代码: #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <time.h> #include <stdlib.h> #include <string.h> void…...

基于centos7脚本一键部署gpmall商城
基于centos7脚本一键部署单节点gpmall商城,该商城可单节点,可集群,可高可用集群部署,VMware17,虚拟机IP:192.168.200.100 将软件包解压到/root目录 [rootlocalhost ~]# ls dist …...

Mac book英特尔系列?M系列?两者有什么区别呢
众所周知,Mac book有M系列,搭载的是苹果自研的M芯片,也有着英特尔系列,搭载的是英特尔的处理器,虽然从 2020 年开始,苹果公司逐步推出了自家研发的 M 系列芯片,并逐渐将 MacBook 产品线过渡到 M…...

Python unstructured库详解:partition_pdf函数完整参数深度解析
Python unstructured库详解:partition_pdf函数完整参数深度解析 1. 简介2. 基础文件处理参数2.1 文件输入参数2.2 页面处理参数 3. 文档解析策略3.1 strategy参数详解3.2 策略选择建议 4. 表格处理参数4.1 表格结构推断 5. 语言处理参数5.1 语言设置 6. 图像处理参数…...

<项目代码>YOLOv8路面病害识别<目标检测>
YOLOv8是一种单阶段(one-stage)检测算法,它将目标检测问题转化为一个回归问题,能够在一次前向传播过程中同时完成目标的分类和定位任务。相较于两阶段检测算法(如Faster R-CNN),YOLOv8具有更高的…...

广告牌和标签学习
效果: 知识学习: entities添加标签label和广告牌billboard label: text:文本添加 font:字体大小和字体类型 fillColor:字体颜色 outlineColor:字体外轮廓颜色 outlineWidth:字体外轮…...
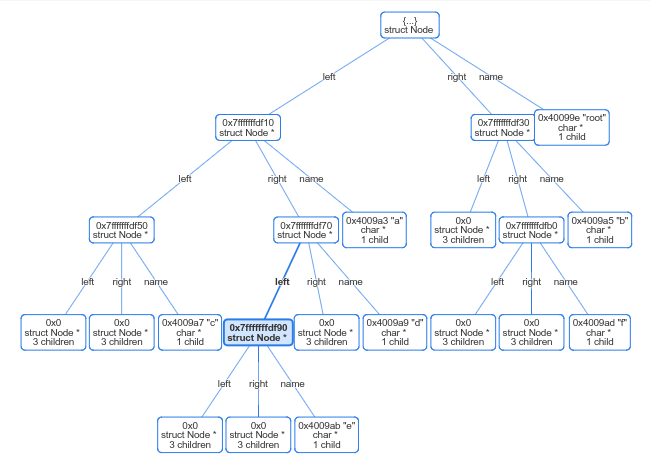
GDB 从裸奔到穿戴整齐
无数次被问道:你在终端下怎么调试更高效?或者怎么在 Vim 里调试?好吧,今天统一回答下,我从来不在 vim 里调试,因为它还不成熟。那除了命令行 GDB 裸奔以外,终端下还有没有更高效的方法ÿ…...

WPF的触发器(Trigger)
WPF(Windows Presentation Foundation)是微软.NET框架的一部分,用于构建Windows客户端应用程序。在WPF中,触发器(Triggers)是一种强大的功能,允许开发者根据控件的状态或属性值来动态改变控件的…...

全能大模型GPT-4o体验和接入教程
GPT-4o体验和接入教程 前言一、原生API二、Python LangchainSpring AI总结 前言 Open AI发布了产品GPT-4o,o表示"omni",全能的意思。 GPT-4o可以实时对音频、视觉和文本进行推理,响应时间平均为 320 毫秒,和人类之间对…...

详解Apache版本、新功能和技术前景
文章目录 一、 版本溯源二、新功能和特性举例1. 模块化和可扩展性增强2. 多处理模块(MPMs)3. 异步支持4. 更细粒度的日志级别控制5. 通用表达式解析器6. HTTP/2支持7. Server Push8. Early Hints9. 更好的SSL/TLS支持10. 更安全的默认设置 三、 技术前景…...

Docker Redis集群3主3从模式
主从集群 docker run -d --name redis-node1 --net host --privilegedtrue -v /home/redis/node1:/data redis:7.0 --cluster-enabled yes --appendonly yes --port 9371docker run -d --name redis-node2 --net host --privilegedtrue -v /home/redis/node2:/data redis:7.0 …...

【Go语言】
type关键字的用法 定义结构体定义接口定义类型别名类型定义类型判断 别名实际上是为了更好地理解代码/ 这里要分点进行记录 使用传值的例子,当两个类型不一样需要进行类型转换 type Myint int // 自定义类型,基于已有的类型自定义一个类型type Myin…...

【Spring Boot】元注解
元注解 1.元注解1.1 Target1.2 Retention1.3 Inherited1.4 Documented1.5 interface 2.自定义注解2.1 创建自定义注解类2.2 实现业务逻辑2.3 使用自定义注解 1.元注解 元注解就是定义注解的注解,是 Java 提供的用于定义注解的基本注解。 注解 说明 Retention是注解…...

基于信号分解和多种深度学习结合的上证指数预测模型
大家好,我是带我去滑雪! 为了给投资者提供更准确的投资建议、帮助政府和监管部门更好地制定相关政策,维护市场稳定,本文对股民情绪和上证指数之间的关系进行更深入的研究,并结合信号分解、优化算法和深度学习对上证指数…...

基于Spring Boot的酒店住宿管理平台
1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理酒店客房管理系统的相关信息成为必然。开发…...

游聚对战平台 三国战纪2012CE修改器修改地址
游聚对战平台 三国战纪2012比较全的一次地址。 工具 ce修改器 自行百度下载 1袖箭 2褐色鸡蛋 3毒堂 4飞盘 5火焰弹 6绿色鸡蛋 7金珠 8毒蝎 9毒镖 10铁莲花 11张陵剑 12张角巾 13太清丹经 14黄石公 15九节杖 16隐身衣 17神仙笔 18 玉蜂术(效果不明)19天师…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
