PID控制原理
PID控制原理
PID控制器是一种经典且广泛应用于工业控制领域的反馈控制器,它由比例(P)、积分(I)和微分(D)三个部分组成。通过对这三个部分的综合调节,PID控制器能够实现对被控对象的精确控制,使系统输出尽可能快速、准确地跟随设定值(目标值)。下面详细介绍PID控制的各个组成部分及其原理。
1. PID控制器的组成
1.1 比例控制(Proportional Control,P)
- 原理: 比例控制器根据当前误差的大小,按比例调整控制输出。误差越大,控制输出越大。
- 数学表达式:

- 作用: 提供与误差大小成正比的调整力度,响应迅速。
1.2 积分控制(Integral Control,I)
- 原理: 积分控制器根据误差随时间的累积(积分)来调整控制输出,用于消除系统的稳态误差。
- 数学表达式:

- 作用: 消除稳态误差,使系统在稳态时误差趋于零
1.3 微分控制(Derivative Control,D)
- 原理: 微分控制器根据误差变化的速率(即误差的导数)来调整控制输出,预测误差的趋势。
- 数学表达式:

- 作用: 提前预判误差变化,减少超调,提高系统的稳定性。
2. PID控制器的总输出
PID控制器的总控制输出是比例、积分和微分三部分之和:

- u(t):控制器的输出,用于驱动被控对象
3. PID各部分的作用及特点
3.1 比例控制(P)
- 优点: 响应迅速,调整简单。
- 缺点: 不能完全消除稳态误差。
3.2 积分控制(I)
- 优点: 能够消除稳态误差。
- 缺点: 可能导致系统响应变慢,增加超调,甚至引起振荡。
3.3 微分控制(D)
- 优点: 改善系统的动态性能,减少超调和振荡。
- 缺点: 对噪声敏感,可能放大高频噪声
4. PID参数的调整
调整PID控制器的三个增益参数 Kp、Ki、Kd对系统性能影响重大。
增大 Kp:
- 系统响应速度加快。
- 超调可能增加,稳定性降低。
增大 Ki:
- 加快消除稳态误差。
- 可能导致超调和振荡增加。
增大 Kd:
- 减少超调,改善稳定性。
- 对噪声敏感,可能引入高频振荡。
常用的参数调整方法:
- 试凑法: 根据经验逐步调整参数,观察系统响应。
- Ziegler-Nichols 方法: 通过实验确定临界增益和临界振荡周期,计算PID参数。
- 数学模型法: 基于系统的数学模型,利用控制理论计算最佳参数。
4. PID控制器的离散实现
在数字控制系统中,PID控制器需要以离散形式实现。
- 误差:
e(k)=设定值(k)−实际值(k) - 积分项(采用梯形积分法):

- 微分项(采用差分近似):

- 控制器输出:

其中:
- k:第 k 个采样时刻
- T:采样周期
5. 注意事项
5.1 积分饱和与抗积分饱和
问题: 长时间的误差累积可能导致积分项过大,造成“积分饱和”,影响系统稳定性。
解决方法:
- 积分限幅: 对积分项设置上下限。
- 抗积分饱和: 当控制输出达到饱和值时,暂停积分项的累积。
5.2 微分噪声处理
问题: 微分项对高频噪声敏感,可能放大测量噪声。
解决方法:
- 低通滤波器: 在微分项前加入滤波器,减小噪声影响。
- 改进算法: 使用带滤波的微分算法。
5.3 采样周期的选择
- 采样周期过长: 可能导致控制滞后,系统响应变慢。
- 采样周期过短: 增加计算负荷,噪声影响显著。
相关文章:

PID控制原理
PID控制原理 PID控制器是一种经典且广泛应用于工业控制领域的反馈控制器,它由比例(P)、积分(I)和微分(D)三个部分组成。通过对这三个部分的综合调节,PID控制器能够实现对被控对象的…...

python 使用 企微机器人发送消息
import requestswecom_bot_webhook ""msg_text "" # 要发送的消息内容""" mentioned_mobile_list : 手机号列表 , 提醒手机号对应的群成员(某个成员) """ res requests.post(wecom_bot_webhook,json{"msgtype"…...
:华为)
ARM/Linux嵌入式面经(五二):华为
文章目录 一面技术面相关问题1. **硬件改进的具体内容是什么?**硬件改进的具体内容深入询问及回答2. **在维护前任师兄的代码时,你遇到了哪些挑战?**问题回答面试官追问及回答3. **在嵌入式系统中,内存泄漏通常有哪些原因?**一、内存泄漏的主要原因二、内存泄漏的具体场景…...

[旧日谈]高清画面撕裂问题考
背景 无边框透明背景透明的窗口,在随着缩放比例非整数倍数放大时的画面发生了露底、撕裂问题。 当我们在使用Qt开发的时候,遇到了一个结构性问题。因为我们的软件是自己做的,所以要自己定义标题栏,所以我们设置了软件为FrameLess…...

Nginx反向代理-域名代理前后端项目部署流程
一、下载Nginx 地址:https://nginx.org/en/download.html 1、稳定版本下载 二、Nginx配置 1、下载文件完成后,解压文件 2、打开文件目录下conf目录,打开找到nginx.conf 3、文件配置 注意:.conf 文件使用文本编辑器编辑后&…...

代码随想录(十二)——图论
并查集 并查集主要有三个功能。 寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上判断两个节点是否在…...

如何通过 Service Mesh 构建高效、安全的微服务系统
1. 引言 1.1.什么是 Service Mesh? Service Mesh 是一种基础架构层,负责处理微服务之间的通信,它通过在每个服务旁边部署代理(通常称为 Sidecar)来捕获和管理服务间的网络流量。这种方式解耦了微服务的业务逻辑和基础…...

MySQL 临时表详解
在 MySQL 中,临时表(Temporary Table)是一种非常有用的工具,可以帮助我们在执行复杂查询时存储临时数据。临时表的存在时间仅限于会话期,当会话结束后,临时表自动销毁。本文将详细讲解 MySQL 临时表的创建、…...

Kafka系列之:Kafka集群新增节点后实现数据均衡
Kafka系列之:Kafka集群新增节点后实现数据均衡 一、背景二、Kafka集群快速负载均衡方案三、按照Topic负载均衡Kafka系列之:使用Kafka Manager实现leader分区平衡和broker节点上分区平衡一、背景 Kafka集群新增节点,要使得每个节点数据均衡,在增加完kafka topic分区后,要进…...

实验:使用Oxygen发布大型手册到Word格式
此前,我曾发表过一篇文章《结构化文档发布的故事和性能调优》,文中讨论了在将大型DITA手册转换为PDF格式时可能遇到的性能挑战及相应的优化策略。 近日,有朋友咨询,若将同样的大型手册输出为MS Word格式,是否也会面临…...
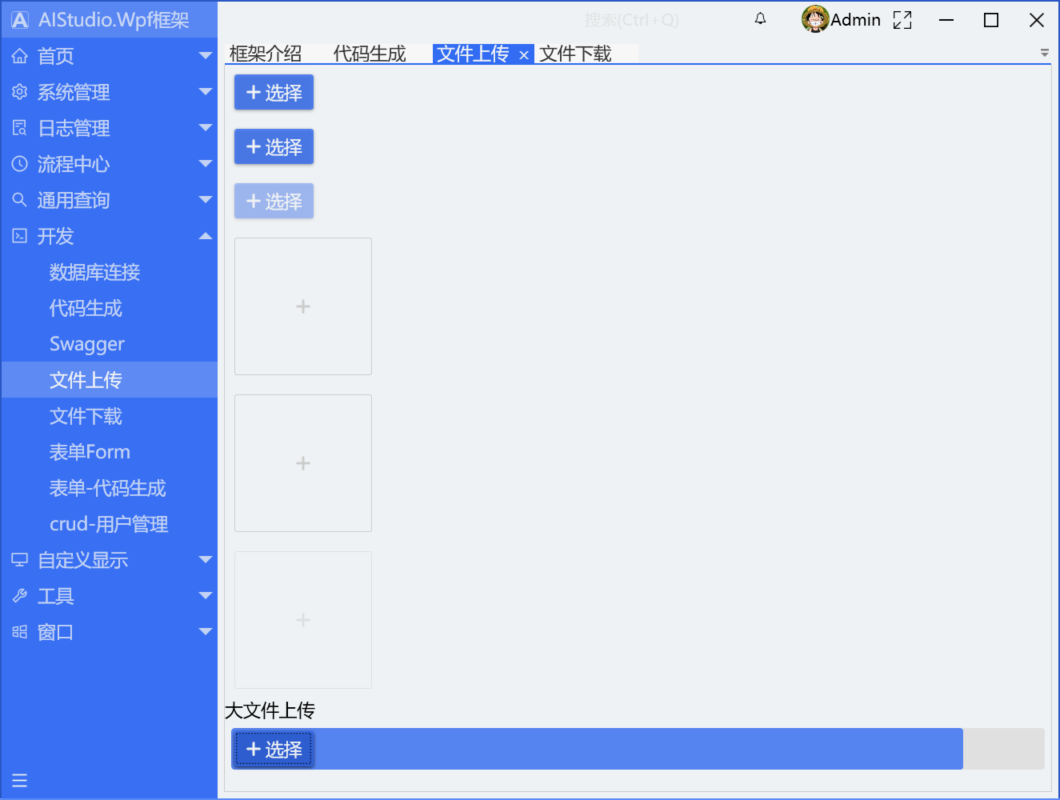
一个基于.NET8+WPF开源的简单的工作流系统
项目介绍 AIStudio.Wpf.AClient 是一个基于 WPF (Windows Presentation Foundation) 构建的客户端框架,专为开发企业级应用而设计。该项目目前版本为 6.0,进行了全面优化和升级,提供了丰富的功能和模块,以满足不同场景下的开发需…...

MFC工控项目实例二十七添加产品参数
承接专栏《MFC工控项目实例二十六创建数据库》 在型号参数界面添加三个参数试验时间、最小值、最大值。变量为double m_edit_time; double m_edit_min; double m_edit_max; 1、在SEAL_PRESSURE.h中添加代码 class CProductPara { public:union{struct{...double m_edit_min;…...

PgSQL常用SQL语句
PgSQL常用SQL语句 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神的孩子都在歌唱 PgSQL是一种开源的关系型数据库管理系统,它是PostgreSQL的一种实现。本文将介绍一些常用的PgSQL SQL语句&a…...
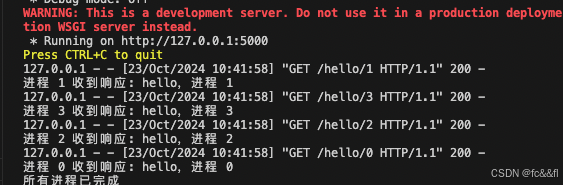
python多线程处理xlsx,多进程访问接口
import pandas as pd from concurrent.futures import ThreadPoolExecutor# 读取Excel文件 file_path scence.xlsx df pd.read_excel(file_path)# 定义每10行处理逻辑 def process_rows(start_idx):end_idx min(start_idx 10, len(df)) # 处理每10行for i in range(start_…...

PDF无法转换成其他格式的常见原因与解决方法解析
在处理PDF文件转换时,用户常常会遇到一些问题,导致无法将PDF转换为其他格式(如Word、Excel、或图片等)。以下是一些常见原因以及解决方法的解析。 ## 一、常见原因 ### 1. **PDF文件的安全性设置** 许多PDF文件在创建时可能设置…...

蓝桥杯第二十场小白入门赛
2.黛玉泡茶 我的思路代码:(但我不知道哪有错误) #include<iostream> #include<vector> #include<algorithm> using namespace std;int main(){int n,m,k,res1;cin>>n>>m>>k;vector<int>num(n1,0…...

K 个一组反转链表
力扣第 25 题:K 个一组反转链表 题目描述 给定一个链表,将链表每k个节点一组进行反转,并返回修改后的链表。如果最后一组节点数少于 k,则保持原顺序。 示例 1: 输入:1 -> 2 -> 3 -> 4 -> 5&…...

#深度学习:从基础到实践
深度学习是人工智能领域近年来最为火热的技术之一。它通过构建由多个隐藏层组成的神经网络模型,能够从海量数据中自动学习特征和表征,在图像识别、自然语言处理、语音识别等领域取得了突破性进展。本文将全面介绍深度学习的基础知识、主要算法和实践应用,帮助您快速…...

Android Kotlin中协程详解
博主前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住也分享一下给大家, 👉点击跳转到教程 前言 Kotlin协程介绍: Kotlin 协程是 Kotlin 语言中的一种用于处理异步编程的机制。它提供了一…...

【webpack学习】
webpack由于历史包袱导致复杂,只要把握关键流程即可 webpack的主要流程loader plugin难点:HMR / 懒加载 原理webpack 的优化手段 构建工具对比 webpack :可以打包任何资源,配置略复杂,适合项目开发rollup࿱…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
