深入理解Allan方差:用体重数据分析误差的时间尺度与稳定性
文章目录
- 1. 什么是Allan方差?
- Allan方差的特点
- 2. Allan方差与传统方差的区别
- 3. 用体重数据举例分析波动性
- 场景A:体重变化较平稳
- 场景B:体重变化波动较大
- 4. Allan方差的计算公式与详细步骤
- 5. 不同时间块长度下的Allan方差计算
- 场景A的Allan方差计算(块长度为1天)
- 场景B的Allan方差计算(块长度为1天)
- 6. Allan偏差与块长度的双对数曲线
- 双对数曲线的解读
- 7. 总结
在日常生活和科学研究中,体重、温度、金融市场波动等数据往往包含复杂的噪声和趋势成分。传统的统计方法(如均值和标准差)在揭示数据动态变化方面存在局限。Allan方差(Allan Variance)作为一种分析时间序列数据稳定性的方法,能够帮助我们深入探究数据在不同时间尺度下的波动特性。本文将详细介绍Allan方差的概念及其计算过程,并通过实际的体重数据示例分析其短期和长期波动性。我们将通过双对数曲线展示Allan方差在不同块长度下的变化,从而全面揭示体重数据的动态特性。
1. 什么是Allan方差?
Allan方差最初被应用于分析频率标准中的噪声特性,特别适用于分析时间序列的长期和短期稳定性。它能够揭示数据在不同时间尺度下的波动特性,从而帮助我们理解数据的动态变化。
Allan方差的特点
与传统的方差不同,Allan方差能够根据不同时间尺度(块长度)分析数据的波动。这意味着我们可以通过调整块长度,分别观察短期和长期的波动特性。Allan方差的这种特性使其在分析数据的稳定性时具有优势。
2. Allan方差与传统方差的区别
传统方差衡量的是数据整体的波动情况,无法分辨短期波动与长期趋势。而Allan方差则通过计算不同块长度下的数据差异,揭示了不同时间尺度上的稳定性。这一特性使得Allan方差在体重管理、温度分析、金融市场波动等领域表现得尤为出色。
3. 用体重数据举例分析波动性
为了更好地理解Allan方差的计算,我们使用一周的体重数据进行分析,假设每天早晨记录体重,并分为两个场景:
场景A:体重变化较平稳
| 天数 | 体重(kg) |
|---|---|
| 第1天 | 70.0 |
| 第2天 | 70.2 |
| 第3天 | 70.1 |
| 第4天 | 70.3 |
| 第5天 | 70.4 |
| 第6天 | 70.3 |
| 第7天 | 70.5 |
场景B:体重变化波动较大
| 天数 | 体重(kg) |
|---|---|
| 第1天 | 70.0 |
| 第2天 | 70.6 |
| 第3天 | 70.1 |
| 第4天 | 70.5 |
| 第5天 | 70.0 |
| 第6天 | 70.6 |
| 第7天 | 70.1 |
场景A中体重变化较为平稳,而场景B中则显示出更显著的波动。
4. Allan方差的计算公式与详细步骤
Allan方差的计算公式如下:
σ y 2 ( τ ) = 1 2 ( N − 1 ) ∑ i = 1 N − 1 ( y ˉ i + 1 − y ˉ i ) 2 \sigma_y^2(\tau) = \frac{1}{2(N - 1)} \sum_{i=1}^{N-1} (\bar{y}_{i+1} - \bar{y}_i)^2 σy2(τ)=2(N−1)1i=1∑N−1(yˉi+1−yˉi)2
其中:
- σ y 2 ( τ ) \sigma_y^2(\tau) σy2(τ) 表示块长度为 τ \tau τ 的Allan方差;
- τ \tau τ 表示时间块长度(如1天、3天等);
- N N N 为数据块的总数;
- y ˉ i \bar{y}_i yˉi 表示第 i i i 个块的平均值。
计算步骤:
- 选择时间块长度 τ \tau τ。
- 按块长度将数据分组,计算每组的平均值。
- 计算相邻时间块的均值差的平方。
- 求和并除以 2 ( N − 1 ) 2(N-1) 2(N−1)。
5. 不同时间块长度下的Allan方差计算
通过选择不同的时间块长度(如1天、3天、7天等),可以分析不同时间尺度下的波动性。例如,当块长度为1天时,主要分析短期波动;块长度为7天时,观察更长时间尺度的趋势变化。
以下为基于场景A和场景B数据的详细计算:
场景A的Allan方差计算(块长度为1天)
-
计算每个时间块的平均值:
- y ˉ 1 = 70.0 \bar{y}_1 = 70.0 yˉ1=70.0, y ˉ 2 = 70.2 \bar{y}_2 = 70.2 yˉ2=70.2, y ˉ 3 = 70.1 \bar{y}_3 = 70.1 yˉ3=70.1, y ˉ 4 = 70.3 \bar{y}_4 = 70.3 yˉ4=70.3, y ˉ 5 = 70.4 \bar{y}_5 = 70.4 yˉ5=70.4, y ˉ 6 = 70.3 \bar{y}_6 = 70.3 yˉ6=70.3, y ˉ 7 = 70.5 \bar{y}_7 = 70.5 yˉ7=70.5
-
计算相邻时间块的均值差的平方:
- ( y ˉ 2 − y ˉ 1 ) 2 = 0.04 (\bar{y}_2 - \bar{y}_1)^2 = 0.04 (yˉ2−yˉ1)2=0.04, ( y ˉ 3 − y ˉ 2 ) 2 = 0.01 (\bar{y}_3 - \bar{y}_2)^2 = 0.01 (yˉ3−yˉ2)2=0.01, ( y ˉ 4 − y ˉ 3 ) 2 = 0.04 (\bar{y}_4 - \bar{y}_3)^2 = 0.04 (yˉ4−yˉ3)2=0.04, ( y ˉ 5 − y ˉ 4 ) 2 = 0.01 (\bar{y}_5 - \bar{y}_4)^2 = 0.01 (yˉ5−yˉ4)2=0.01, ( y ˉ 6 − y ˉ 5 ) 2 = 0.01 (\bar{y}_6 - \bar{y}_5)^2 = 0.01 (yˉ6−yˉ5)2=0.01, ( y ˉ 7 − y ˉ 6 ) 2 = 0.04 (\bar{y}_7 - \bar{y}_6)^2 = 0.04 (yˉ7−yˉ6)2=0.04
-
计算Allan方差:
σ y 2 ( τ ) = 1 2 × 6 ( 0.04 + 0.01 + 0.04 + 0.01 + 0.01 + 0.04 ) = 0.15 12 = 0.0125 \sigma_y^2(\tau) = \frac{1}{2 \times 6} (0.04 + 0.01 + 0.04 + 0.01 + 0.01 + 0.04) = \frac{0.15}{12} = 0.0125 σy2(τ)=2×61(0.04+0.01+0.04+0.01+0.01+0.04)=120.15=0.0125 -
计算Allan偏差:
σ y ( τ ) = 0.0125 ≈ 0.1118 kg \sigma_y(\tau) = \sqrt{0.0125} \approx 0.1118 \text{ kg} σy(τ)=0.0125≈0.1118 kg
场景B的Allan方差计算(块长度为1天)
同样的方法计算得出:
- Allan方差为 0.1358 0.1358 0.1358;
- Allan偏差为 σ y ( τ ) ≈ 0.3687 kg \sigma_y(\tau) \approx 0.3687 \text{ kg} σy(τ)≈0.3687 kg。
6. Allan偏差与块长度的双对数曲线
为了直观展示波动性,我们通常绘制Allan偏差与块长度的双对数曲线。假设我们分别计算了1天、2天、3天等不同块长度的Allan方差,并开方得到Allan偏差。
双对数曲线的解读
- 负斜率:块长度增加时,Allan偏差下降,表示短期波动显著,随着时间延长趋于平稳。
- 正斜率:块长度增加时,Allan偏差上升,说明数据可能存在长期趋势或周期性变化。
- 水平段:波动性变化较小,数据的波动相对随机且无显著趋势。
7. 总结
Allan方差能够帮助我们揭示数据在不同时间尺度下的波动特性。通过计算和分析体重数据的Allan方差,我们展示了其在实际应用中的效果。进一步,通过双对数曲线的绘制,我们能更深入理解和应用Allan方差,在更广泛的数据分析中发挥作用。
应用实例:
- 体重管理:Allan方差可以帮助判断体重变化的稳定性,识别出短期波动与长期趋势。
- 金融数据分析:通过不同时间尺度的Allan方差,可以分析市场的短期波动性和长期趋势。
- 温度监测:Allan方差可用于分析温度数据的波动特性,识别季节性变化或长期趋势。
Allan方差不仅在科研中具有重要的应用价值,在日常生活中同样能提供有力的数据分析支持。通过深入理解和应用Allan方差,我们可以更精准地分析和解释数据的动态变化,提升数据分析的深度与广度。
相关文章:

深入理解Allan方差:用体重数据分析误差的时间尺度与稳定性
文章目录 1. 什么是Allan方差?Allan方差的特点 2. Allan方差与传统方差的区别3. 用体重数据举例分析波动性场景A:体重变化较平稳场景B:体重变化波动较大 4. Allan方差的计算公式与详细步骤5. 不同时间块长度下的Allan方差计算场景A的Allan方差…...

Elasticsearch 解析:倒排索引机制/字段类型/语法/常见问题
Elasticsearch 是一个分布式的开源搜索引擎,广泛用于全文搜索、分析和数据存储。它基于 Apache Lucene 构建,支持 RESTful 风格的 API,使得开发者能够高效地存储和检索数据。本文将详细讲解 Elasticsearch 的基本原理,特别是其倒排…...

数字后端零基础入门系列 | Innovus零基础LAB学习Day5
###Module 12 RC参数提取和时序分析 数字后端零基础入门系列 | Innovus零基础LAB学习Day4 数字后端零基础入门系列 | Innovus零基础LAB学习Day3 数字后端零基础入门系列 | Innovus零基础LAB学习Day2 数字后端零基础入门系列 | Innovus零基础LAB学习Day1 ###LAB12-1 这个章节…...

Redis 内存回收策略小结
Redis 内存回收策略 及时回收内存中不需要的数据,能有效地保持性能和防止内存溢出。Redis内存回收主要有两种场景 删除过期的键值对内存使用达到maxmemory时触发回收策略 删除过期的键值对 惰性删除: 在查询时如果发现 该键值对已经过期则执行删除操作…...

React常用前端框架合集
React 是 Facebook 开发的一款用于构建用户界面的 JavaScript 库。由于其高效、灵活的特性,React 成为了目前最流行的前端框架之一。为了帮助开发者更好地利用 React 构建应用,市场上涌现了许多优秀的辅助工具和框架。本文将详细介绍几个常用的 React 前…...

python对文件的读写操作
任务:读取文件夹下的批量txt数据,并将其写入到对应的word文档中。 txt文件中包含:编号、报告内容和表格数据。写入到word当中:编号、报告内容、表格数据、人格雷达图以及对应的详细说明(详细说明是根据表格中的标识那一列中的加号…...
)
Redis工具类(解决缓存穿透、缓存击穿)
文章目录 前言IBloomFilterObjectMapUtilsCacheClient使用示例具体业务的布隆过滤器控制层服务层 前言 该工具类包含以下功能: 1.将任意对象存储在 hash 类型的 key 中,并可以设置 TTL 2.将任意对象存储在 hash 类型的 key 中,并且可以设置…...

Air780E量产binpkg文件的获取方法
Air780E量产binpkg文件如何获取呢?操作方法如下。 一、背景 最近luatos开发客户增多,客户在量产烧录的时候需要binpkg文件,但是有些客户不知道binpkg文件是什么,在哪里获取,是否可以用soc文件提取出来,使…...

C++STL之stack
1.stack的使用 函数说明 接口说明 stack() 构造空的栈 empty() 检测 stack 是否为空 size() 返回 stack 中元素的个数 top() 返回栈顶元素的引用 push() 将元素 val 压入 stack 中 pop() 将 stack 中尾部的元素弹出 2.stack的模拟实现 #include<vector> namespace abc { …...

git的学习之远程进行操作
1.代码托管GitHub:充当中央服务器仓库的角色 2.git远程进行操作 3.配置本地服务器的公钥 4.推送 5.git远程操作 pull .gitignore 6.给命令配置别名 git config --global alias.st status 7.标签管理 git tag -a [name] -m "XXX" [commit_id] 操作标签…...

蓝桥杯普及题
[蓝桥杯 2024 省 B] 好数 题目描述 一个整数如果按从低位到高位的顺序,奇数位(个位、百位、万位……)上的数字是奇数,偶数位(十位、千位、十万位……)上的数字是偶数,我们就称之为“好数”。 给定一个正整数 N N N,请计算从 1 1...

Spreadsheet导出excel
记录下常用的方法 数字转字符:Coordinate::stringFromColumnIndex(27); 输出 AA字符转数字:Coordinate::columnIndexFromString(AA); 输出27设置单元格式 eg:(设置为保留两位小数点) $sheet->getStyle($columnLetter)->getNumberFormat()->set…...

Leetcode|454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和
15.三数之和 哈希解法: 用俩个for循环求出,所需的a和b,再用哈希表,判断剩余的那个c是否在数组 class Solution { public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>…...

使用ceph-csi把ceph-fs做为k8s的storageclass使用
背景 ceph三节点集群除了做为对象存储使用,计划使用cephfs替代掉k8s里面现有的nfs-storageclass。 思路 整体实现参考ceph官方的ceph csi实现,这套环境是arm架构的,即ceph和k8s都是在arm上实现。实测下来也兼容。 ceph-fs有两种两种挂载方…...
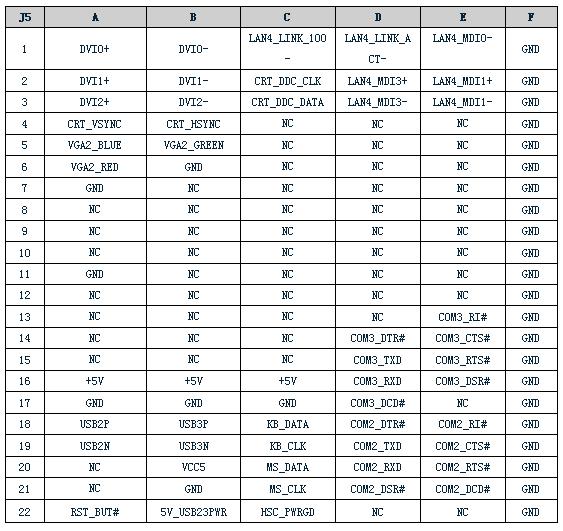
太速科技-212-RCP-601 CPCI刀片计算机
RCP-601 CPCI刀片计算机 一、产品简介 RCP-601是一款基于Intel i7双核四线程的高性能CPCI刀片式计算机,同时,将CPCI产品的欧卡结构及其可靠性、可维护性、可管理性与计算机的抗振动、抗冲击、抗宽温环境急剧变化等恶劣环境特性进行融合。产品特别…...

【解决 Windows 下 SSH “Bad owner or permissions“ 错误及端口转发问题详解】
使用 Windows 连接远程服务器出现 Bad owner or permissions 错误及解决方案 在 Windows 系统上连接远程服务器时,使用 SSH 可能会遇到以下错误: Bad owner or permissions on C:\Users\username/.ssh/config这个问题通常是由于 SSH 配置文件 .ssh/con…...

使用预训练的BERT进行金融领域问答
获取更多完整项目代码数据集,点此加入免费社区群 : 首页-置顶必看 1. 项目简介 本项目旨在开发并优化一个基于预训练BERT模型的问答系统,专注于金融领域的应用。随着金融市场信息复杂性和规模的增加,传统的信息检索方法难以高效…...

ReactOS系统中MM_REGION结构体的声明
ReactOS系统中MM_REGION结构体的声明 ReactOS系统中MM_REGION结构体的声明 文章目录 ReactOS系统中MM_REGION结构体的声明MM_REGION MM_REGION typedef struct _MM_REGION {ULONG Type;//MEM_COMMIT,MEM_RESERVEULONG Protect;//PAGE_READONLYY,PAGE_READ_WRITEULONG Length;…...

web相关知识学习笔记
一, web安全属于网络信息安全的一个分支,www即全球广域网,也叫万维网,是一个分布式图形信息系统 二, 1.①安全领域,通常将用户端(浏览器端)称为前端,服务器端称为后端 ②…...

App测试环境部署
一.JDK安装 参考以下AndroidDevTools - Android开发工具 Android SDK下载 Android Studio下载 Gradle下载 SDK Tools下载 二.SDK安装 安装地址:https://www.androiddevtools.cn/ 解压 环境变量配置 变量名:ANDROID_SDK_HOME 参考步骤: A…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
