Word中Normal.dotm样式模板文件
Normal.dotm文档
首先将自己电脑中C:\Users\自己电脑用户名\AppData\Roaming\Microsoft\Templates路径下的Normal.dotm文件做备份,在下载本文中的Normal.dotm文件,进行替换,重新打开word即可使用。
字体样式如下(可自行修改):

做备份如下:

再进行替换:

相关文章:

Word中Normal.dotm样式模板文件
Normal.dotm文档 首先将自己电脑中C:\Users\自己电脑用户名\AppData\Roaming\Microsoft\Templates路径下的Normal.dotm文件做备份,在下载本文中的Normal.dotm文件,进行替换,重新打开word即可使用。 字体样式如下(可自行修改&#…...

生成式 AI 与向量搜索如何扩大零售运营:巨大潜力尚待挖掘
在竞争日益激烈的零售领域,行业领导者始终在探索革新客户体验和优化运营的新途径,而生成式 AI 和向量搜索在这方面将大有可为。从个性化营销到高效库存管理,二者在零售领域的诸多应用场景中都展现出变革性潜力,已成为保持行业领先…...

WonderWorld:斯坦福与 MIT 联手打造实时交互生成图像,单图秒变 3D 虚拟世界
❤️ 如果你也关注大模型与 AI 的发展现状,且对大模型应用开发非常感兴趣,我会快速跟你分享最新的感兴趣的 AI 应用和热点信息,也会不定期分享自己的想法和开源实例,欢迎关注我哦! 🥦 微信公众号ÿ…...

2024年【制冷与空调设备安装修理】考试内容及制冷与空调设备安装修理最新解析
题库来源:安全生产模拟考试一点通公众号小程序 制冷与空调设备安装修理考试内容是安全生产模拟考试一点通总题库中生成的一套制冷与空调设备安装修理最新解析,安全生产模拟考试一点通上制冷与空调设备安装修理作业手机同步练习。2024年【制冷与空调设备…...

PHP const 和 define主要区别
在PHP中,const 和 define 都用于定义常量,但它们有一些关键的区别。以下是它们之间的主要不同点: 定义方式: const:在定义常量时,不需要使用函数形式,而是直接赋值。 const MY_CONSTANT som…...

期中前学习复习总结
期中前终于把每一科的本质给搞明白了。这篇文章也将各学科剖分为两部分。 目录 本质 学法 从问题或条件出发思考问题 从条件出发思考问题 从结论/问题出发思考问题 整理知识与反向押题法 反向押题法 本质 作者是一个理科脑,什么都觉得只要我脑子够新东西我…...
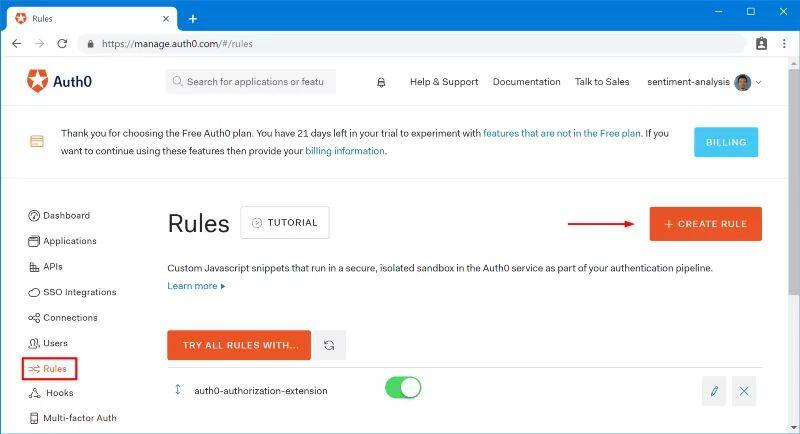
K8S如何基于Istio重新实现微服务
K8S如何基于Istio重新实现微服务 认识 Istio前言Istio 的理念Istio 的架构数据平面控制平面服务与 Istio 的关系 Istio 实践环境准备安装 Helm安装Istio 使用 Istio 代理运行应用情感分析应用的架构使用 Istio 代理运行应用Sidecar 注入Ingress 网关网关资源VirtualService 资源…...

MediaPipe 与 OpenCV 的结合——给心爱的人画一个爱心吧~
目录 概要 实现思路 整体代码实现 效果展示 总结 概要 实时手部检测与绘图应用,通过摄像头捕捉视频流,使用 MediaPipe 识别手部关键点,判断食指是否伸展且其他手指是否弯曲,在满足条件时在画布上绘制圆点,并实时显…...

心觉:成大事,不怕慢,就怕站
Hi,我是心觉,带你用潜意识化解各种焦虑、内耗,建立无敌自信;教你财富精准显化的实操方法;关注我,伴你一路成长! 每日一省写作213/1000天 今天咱们聊聊一个不太花哨,但超重要的话题:…...

练习LabVIEW第二十三题
学习目标: 刚学了LabVIEW,在网上找了些题,练习一下LabVIEW,有不对不好不足的地方欢迎指正! 第二十三题: 建立一个枚举控件,其内容为张三、李四、王五共三位先生,要求当枚举控件显…...
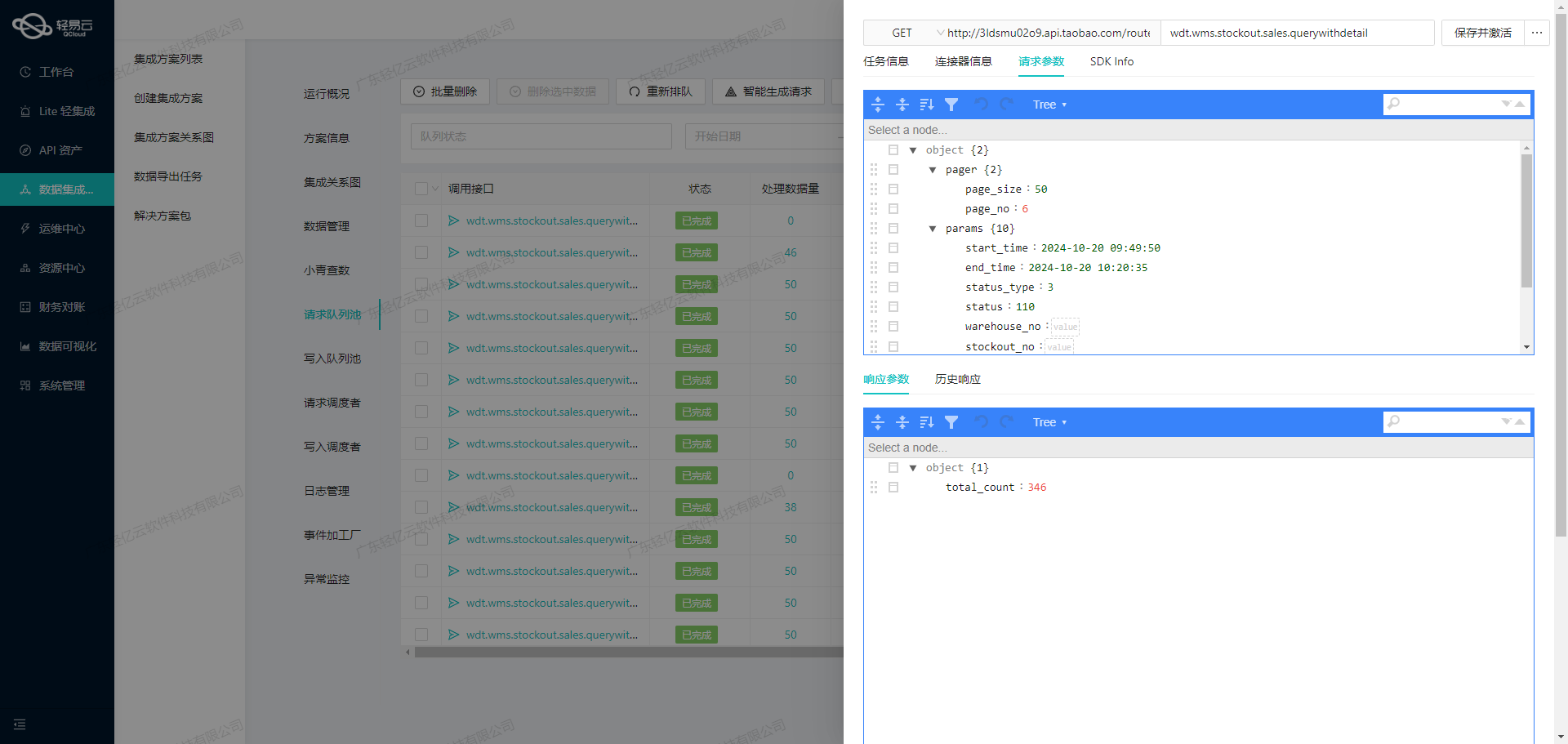
集成对接案例分享:金蝶云与聚水潭数据对接
金蝶云星空与聚水潭的采购入库单数据集成案例分享 在企业信息化管理中,数据的高效流转和准确对接是提升业务效率的关键。本文将深入探讨如何通过轻易云数据集成平台,实现金蝶云星空中的采购入库单数据无缝对接到聚水潭系统中的其他入库单。 本次集成方…...

高级主题-灾难恢复与业务连续性
第一节:灾难恢复与业务连续性 灾难恢复与业务连续性概述 灾难恢复(Disaster Recovery, DR)和业务连续性(Business Continuity, BC)是确保企业能够在遭遇灾难或意外中断后迅速恢复正常运营的关键措施。以下是一些基本…...

R语言实现随机森林分析:从入门到精通
随机森林(Random Forest)是一种流行的机器学习算法,它通过集成多个决策树来提高预测的准确性和鲁棒性。在R语言中,我们可以使用randomForest包来实现随机森林分析。本文将详细介绍如何使用R语言进行随机森林分析,包括数…...

【vs2022】windows可用的依赖预编译库
ffmpeg 、x264 、x265 等。obs是基于qt6+vs2022+64bit obs的官网传统构建已经不用了obs的s2022构建OBS Deps Build 2024-09-12FFmpeg4.4 库,x64 可用。...
:自动化基础设施管理的未来)
基础设施即代码(IaC):自动化基础设施管理的未来
随着云计算和大规模分布式系统的迅速发展,手动管理和配置基础设施的传统方式已逐渐跟不上快速迭代的步伐。于是,基础设施即代码(Infrastructure as Code,IaC)作为一种创新实践,成为现代运维管理的基础。IaC不仅提高了基础设施的配置速度,还提升了系统的一致性和可重复性…...

C# 创建型设计模式----原型模式
1、值类型与引用类型、深拷贝与浅拷贝。 在了解原型模式前得先对这四个知识点有些了解。我先简单介绍一下这四个知识点。 1.1 值类型与引用类型(C#仅有这两种数据类型) 值类型: 常见的值类型:int、long、short、byte、float、double、bool、char、Struct…...

Python数据分析NumPy和pandas(十五、pandas 数据加载、存储和文件格式)
大多数时候,我们要处理分析的数据是存储在不同格式的文件中的,有txt、csv、excel、json、xml以及二进制等磁盘文件格式,还有时候是从数据库以及从Web API中交互获取要处理的数据。现在开始学习如何用pandas从以上内容中输入和输出数据。 读取…...

正则表达式以及密码匹配案例手机号码脱敏案例
目录 正则表达式 什么是正则表达式 语法 定义变量 test方法 exec方法 replace方法 match方法 修饰符 元字符 边界符 单词边界 字符串边界 边界符:^ 边界符:$ 量词 * ? {n} {n,} {n,m} 字符类 []匹配字符集合 .匹配除换行符之外的…...

五、数组切片make
数组&切片&make 1. 数组2. 多维数组3. 切片3.1 直接声明新的切片函数构造切片3.3 思考题3.4 切片和数组的异同 4. 切片的复制5. map5.1 遍历map5.2 删除5.3 线程安全的map 6. nil7. new和make 1. 数组 数组是一个由固定长度的特定类型元素组成的序列,一个数…...

SSA-CNN-LSTM-MATT多头注意力机制多特征分类预测
SSA-CNN-LSTM-MATT多头注意力机制多特征分类预测 目录 SSA-CNN-LSTM-MATT多头注意力机制多特征分类预测分类效果基本介绍程序设计参考资料 分类效果 基本介绍 1.Matlab实现SSA-CNN-LSTM-MATT麻雀算法优化卷积神经网络-长短期记忆神经网络融合多头注意力机制多特征分类预测&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
