LeetCode 每日一题 2024/10/21-2024/10/27
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步
目录
- 10/21 910. 最小差值 II
- 10/22 3184. 构成整天的下标对数目 I
- 10/23 3185. 构成整天的下标对数目 II
- 10/24 3175. 找到连续赢 K 场比赛的第一位玩家
- 10/25 3180. 执行操作可获得的最大总奖励 I
- 10/26 3181. 执行操作可获得的最大总奖励 II
- 10/27 684. 冗余连接
10/21 910. 最小差值 II
从小到大排列 小的尽量+k 大的-k
最小值mi 最大值ma
从头遍历位置i 假设nums[i]是最大一个+k的值
那么当前情况最大值为 max(nums[i]+k,ma-k)
最小值为min(nums[i+1]-k,mi+k)
更新当前情况的差值
def smallestRangeII(nums, k):""":type nums: List[int]:type k: int:rtype: int"""nums.sort()mi,ma=nums[0],nums[-1]ans = ma-min=len(nums)for i in range(n-1):cur,nxt = nums[i],nums[i+1]ans = min(ans,max(cur+k,ma-k)-min(nxt-k,mi+k))return ans10/22 3184. 构成整天的下标对数目 I
计算每个小时除以24的余数
余数相加为24的可以匹配
余数为0和12 在自己组内匹配
def countCompleteDayPairs(hours):""":type hours: List[int]:rtype: int"""l=[0]*24for h in hours:l[h%24]+=1ans = 0for i in range(1,12):ans += l[i]*l[24-i]ans+=l[0]*(l[0]-1)//2+l[12]*(l[12]-1)//2return ans10/23 3185. 构成整天的下标对数目 II
计算每个小时除以24的余数
余数相加为24的可以匹配
余数为0和12 在自己组内匹配
def countCompleteDayPairs(hours):""":type hours: List[int]:rtype: int"""l=[0]*24for h in hours:l[h%24]+=1ans = 0for i in range(1,12):ans += l[i]*l[24-i]ans+=l[0]*(l[0]-1)//2+l[12]*(l[12]-1)//2return ans10/24 3175. 找到连续赢 K 场比赛的第一位玩家
从头遍历 i 直至遇到大于他的j
如果此时已经赢了k场那么返回i
否则从j开始继续往后赢
如果到最后还没有达到k 此时的i必定是最大值 返回
def findWinningPlayer(skills, k):""":type skills: List[int]:type k: int:rtype: int"""n=len(skills)i = 0lasti = 0cnt = 0while i<n:j = i+1while j<n and skills[i]>skills[j] and cnt<k:cnt+=1j+=1if cnt==k:return icnt=1lasti = ii=jreturn lasti10/25 3180. 执行操作可获得的最大总奖励 I
从小到大排序
dp[k]表示奖励k是否可以获得
最大值为mx 能够得到的奖励不超过2*m-1
对于当前值x 最多可以到达k=x~2x-1 如果k-x存在 那么说明k可以得到
def maxTotalReward(rewardValues):""":type rewardValues: List[int]:rtype: int"""rewardValues.sort()mx = rewardValues[-1]dp=[0]*(2*mx)dp[0]=1for x in rewardValues:for k in range(2*x-1,x-1,-1):if dp[k-x]==1:dp[k]=1for i in range(len(dp)-1,-1,-1):if dp[i]==1:return i10/26 3181. 执行操作可获得的最大总奖励 II
从小到大排序 dp[k]判断奖励k是否可以获得
遍历value x 对k=x,2x-1一次查看
def maxTotalReward(rewardValues):""":type rewardValues: List[int]:rtype: int"""rewardValues.sort()if len(rewardValues)>=2 and rewardValues[-2]==rewardValues[-1]-1:return 2*rewardValues[-1]-1dp = 1for x in rewardValues:dp |= (dp & ((1<<x)-1))<<xreturn dp.bit_length()-110/27 684. 冗余连接
并查集
遍历每一条边 比树多一条边
如果两个点已经连通说明这条边是多余的
def findRedundantConnection(edges):""":type edges: List[List[int]]:rtype: List[int]"""n=len(edges)p = list(range(n+1))def find(i):if p[i]!=i:p[i]=find(p[i])return p[i]def union(i,j):p[find(i)]=find(j)for i,j in edges:if find(i)!=find(j):union(i,j)else:return [i,j]return []相关文章:

LeetCode 每日一题 2024/10/21-2024/10/27
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 10/21 910. 最小差值 II10/22 3184. 构成整天的下标对数目 I10/23 3185. 构成整天的下标对数目 II10/24 3175. 找到连续赢 K 场比赛的第一位玩家10/25 3180. 执行操作可获得…...

不到1500元的I卡可以玩转3A大作吗?撼与科技Intel Arc A750显卡游戏性能实
一、前言 还记得2022年10月的时候,英特尔发布了Arc A750和A770显卡,和此前所发布的DG1、A380不同,这两张显卡可以说是真正意义上的游戏显卡。不知不觉间,两年已经过去了,在这两年期间,英特尔不仅在积极地打…...

STK与MATLAB互联——仿真导航卫星与地面用户间距离和仰角参数
文章目录 构建GPS星座创建单个PRN的GPS卫星创建GPS星座,并为其添加发射机 北斗星座构建搭建低轨铱星星座构建一颗轨道高度为800km/1000km/1200km的低轨卫星构建一颗轨道高度为800km/1000km/1200km的低轨卫星建立地面站,可见性分析确定地面站坐标分析单颗…...

js面试问题笔记(一)
一.热门js面试 1.简述同步和异步的区别? 同步: 浏览器访问服务器请求,用户看到页面刷新 ,重新发请求,等请求完,页面刷新,新内容出现,用户看到新内容,进行下一步操作 异步: 浏览器访问服务器请求,用户正常操作,浏览器后端进行请求,等请求完,页面不刷新,新内容也会出现,用户看到…...

pip 和 pipx 的主要区别?
特性pippipx用途用于安装Python库或命令行应用程序,可以安装带entry points的库专门用于安装和管理Python命令行工具,每个工具都在隔离的虚拟环境中运行虚拟环境不自动创建虚拟环境,需要手动使用 venv 或 virtualenv 创建自动为每个安装的工具…...

4457M数字示波器
_XLT新利通_ 4457M数字示波器 带宽500MHz到3GHz 4457M系列数字示波器产品,包含4457DM/EM/FM/GM四个产品型号,模拟通道数4、8个,带宽500MHz到3GHz,最高采样率10GSa/s,垂直分辨率8bit,最大存储深度2Gpts。…...

【永中软件-注册/登录安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

Tomcat作为web的优缺点
文章目录 优点缺点 优点 开源:Tomcat是Apache软件基金会的一个项目,这意味着它是免费且开放源代码的。这为开发者提供了高度的自由度来修改和扩展其功能。 轻量级:与一些全功能的Java EE应用服务器(如IBM WebSphere, Oracle WebL…...

conda虚拟环境中安装cuda方法、遇到的问题
conda虚拟环境中安装cuda方法、遇到的问题 文章目录 conda虚拟环境中安装cuda方法、遇到的问题conda虚拟环境中安装cudacuda.h和cuda_runtime.hpytorch运行时的CUDA版本其他问题检查包冲突nvcc -V和nvidia-smi显示的版本不一致cuda路径 conda虚拟环境中安装cuda 参考文章&…...

【CPN TOOLS建模学习】设置变迁的属性
使用Tab键在属性之间进行切换 与一个变迁相关联的四个铭文,均为可选项: 变迁名称守卫(Guard)时间代码段 变迁延迟必须是一个正整数表达式。该表达式前面加上,这意味着时间铭文的形式为 delayexpr。在添加时间铭文之前,铭文的默…...

一个简单的例子,说明Matrix类的妙用
在Android、前端或者别的平台的软件开发中,有时会遇到类似如下需求: 将某个图片显示到指定的区域;要求不改变图片本身的宽高比,进行缩放;要求最大限度的居中填充到显示区域。 以下示意图可以简单描绘该需求 以Androi…...

【C++】类和对象(四):析构函数
大家好,我是苏貝,本篇博客带大家了解C的析构函数,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 1. 概念2. 特性 1. 概念 通过前面构造函数的学习,我们知道一个对象是怎么来的…...

linux中各目录作用及介绍
目录 1 /usr 1 /usr /usr 是 Unix-like 操作系统中的一个重要目录之一,代表可共享的用户资源(User System Resources)或 Unix Software Resource(UNIX 软件资源)。 /usr 目录通常包含了系统的许多可共享资源…...
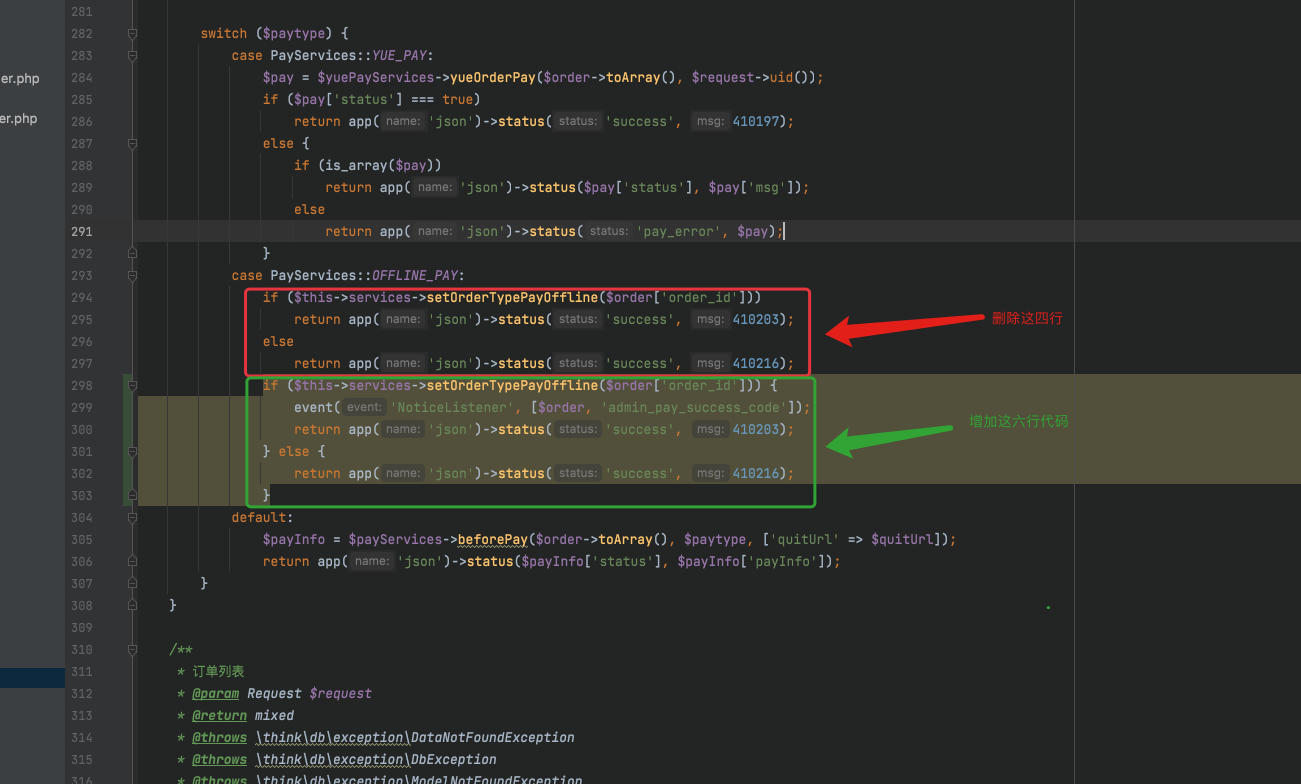
v4.7版本使用线下付款方式不给管理员发送新订单通知问题修复
在app/api/controller/v1/order/StoreOrderController.php文件中,将红框内的代码注释,加上绿框的代码即可修复 if ($this->services->setOrderTypePayOffline($order[order_id])) {event(NoticeListener, [$order, admin_pay_success_code]);retur…...

vue3中mitt和pinia的区别和主要用途,是否有可重合的部分?
在 Vue 中,Mitt 和 Pinia 是两个不同的工具,它们的主要用途和功能有所不同,但在某些方面也存在重合的部分。 区别 Mitt: Mitt 是一个简单而强大的事件总线库,用于在组件之间进行事件的发布和订阅。 它提供了一种简洁…...

飞书文档解除复制限制
解除飞书文档没有编辑器权限限制复制功能方法 方法一:使用插件 方法二: 通过调试工具删除所有的copy事件 使用插件 缺点: 只有markdown格式,如果需要其他格式需要再通过Typora等markdown编辑器转pdf,word等格式 安装插件 Cloud Do…...

vue3中ref和reactive的用法,区别和优缺点,以及使用场景
写在前头: reactive定义的数据只能修改里面的属性,不能将整个数据替换,实在要替换请使用 Object.assign(obj1, obj2);举个例子 这种写法无法直接改变obj1 let obj1 reactive({name: 猫,age: 2, });obj1 {name: 猪,age: 2, } 正确的写法…...
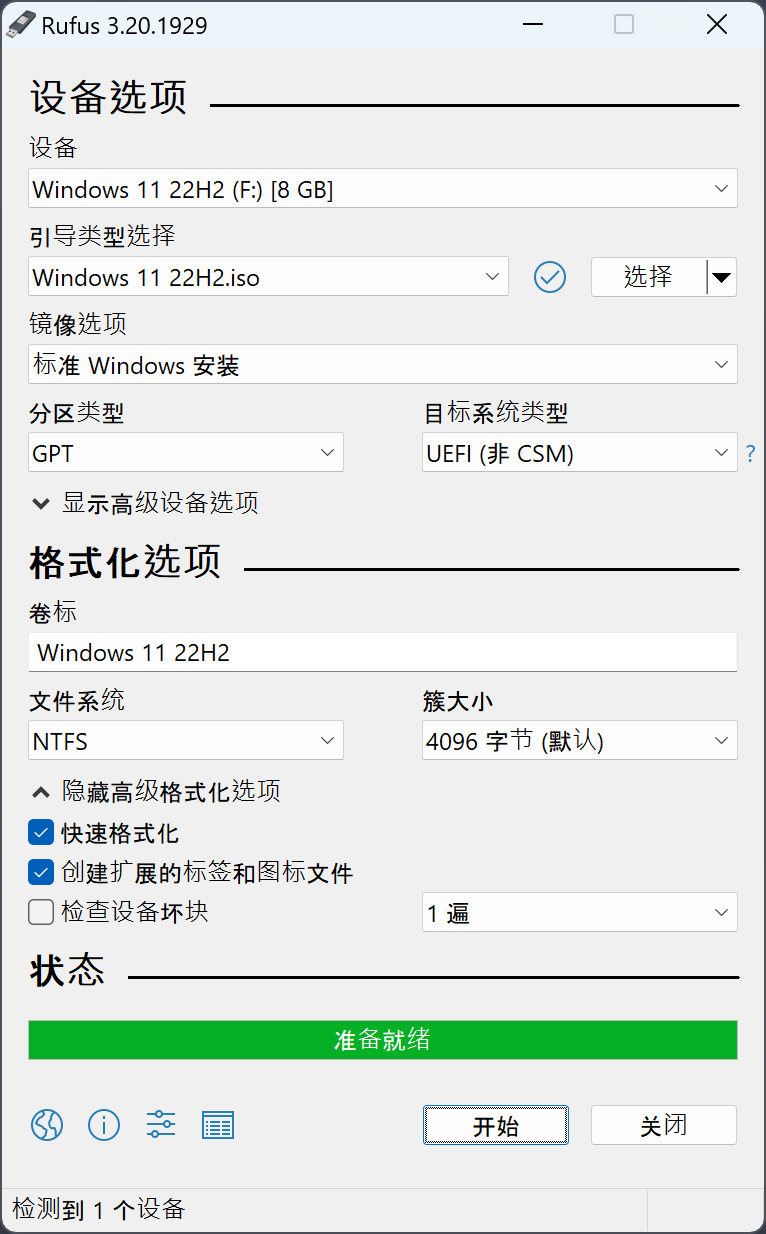
电脑技巧:Rufus——最佳USB启动盘制作工具指南
目录 一、功能强大,兼容性广泛 二、界面友好,操作简便 三、快速高效,高度可定制 四、安全可靠,社区活跃 在日常的电脑使用中,无论是为了安装操作系统、修复系统故障还是进行其他需要可引导媒体的任务,拥…...

vue的基本使用
简介 vue组件 三个部分组成:结构、样式、逻辑文本插值 类似于java的spel表达式属性绑定 綁定是单向绑定的,修改输入框无法改变原本的,只能读,不能写 <input :value="name" placeholder="Type your name"><script> export default {name: H…...

C#高级:利用 CancellationToken 实现方法超时控制,提升应用响应性
完整版: using System; using System.Threading; using System.Threading.Tasks;public class Program {public static async Task Main(){var cts new CancellationTokenSource();// 设置超时时间为10秒cts.CancelAfter(TimeSpan.FromSeconds(3));try{var resul…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
