【数据结构和算法】三、动态规划原理讲解与实战演练
目录
1、什么是动态规划?
2、动态规划实战演练
2.1 力扣题之爬楼梯问题
(1)解题思路1:
(2)解题思路2:
(3)动态规划(DP):解题思路
(4)动态规划理论
2.2 力扣题之海盗船长
(1)解题思路1:
(2)解题思路2:
(3)动态规划:解题思路3:
1、什么是动态规划?
动态规划(Dynamic Programming,DP)是把复杂问题分解为简单的子问题的求解方法。
动态规划的基本思想虽然简单,但分解的子问题很多都不一样。所以需要多做一些练习,接触并了解各种子问题及分解的思路,结合着不同数据结构,才能逐渐掌握DP的技巧。
所以,DP归纳起来就是多做练习,多思考,逐渐摸索题目的思考逻辑和优化思路。才能掌握使用DP解题的技巧。
从实际问题出发,分几步走,不断练习、迭代熟练:
- 暴力求解(枚举)
- 拆分子问题(DP)解法
- DP原理与题型相结合的分析
2、动态规划实战演练
2.1 力扣题之爬楼梯问题
以力扣著名的题“爬楼梯”为例子:
-
爬楼梯问题: . - 力扣(LeetCode)
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶提示:
1 <= n <= 45
(1)解题思路1:
暴力求解,排列所有1,2的组合。
寻找总和为n的,不同数字长度的组合。
from itertools import productdef climbStairs(n):pms = []for rep in range(1,n+1):permutations = list(product([1,2],repeat=rep))for pm in permutations:if sum(pm) == n:pms.append(pm)return len(pms)※ itertools是python为高效循环而创建迭代器的函数库 。product就是一个笛卡尔积(嵌套for循环)功能实现的函数。
- 时间复杂度O(n^3)
- 空间复杂度O(n)
(2)解题思路2:
问题寻找的是爬楼梯的方法数量,而不是具体统计每次走几阶。
所以问题关注的是每次爬1阶、爬2阶两种走法的组合上。
假设n=3,可以直接排列一下相应的组合
3 = 1 + 1 + 1 3 = 2 + 1 3 = 1 + 2简单直观,但我们要寻找的爬楼梯的规律。似乎还没有发现,继续增加n的数量~
当n=4:
4 = 1 + 1 + 1 + 1 4 = 2 + 1 + 1 4 = 1 + 2 + 14 = 1 + 1 + 2 4 = 2 + 2当n=5时:
5 = 1 + 1 + 1 + 1 + 1 5 = 2 + 1 + 1 + 1 5 = 1 + 2 + 1 + 15 = 1 + 1 + 2 + 1 5 = 2 + 2 + 15 = 1 + 1 + 1 + 2 5 = 2 + 1 + 2 5 = 1 + 2 + 2排列组合的方式,让我们似乎观察到了数值的规律。那就是n阶的走法,包含了n-1阶和n-2阶的走法。且 n阶的走法 = (n-1)阶走法 + (n-2)阶走法
简单的循环遍历就可以完成走法的累加:
n = 5 n1,n2 = 1,2 # n=1和n=2情况下的走法 res = 0 for i in range(3, n+1): # 从n=3时开始,直到nres = n1 + n2n1 = n2n2 = res print(res)测试下n=6,结果(n-1) + (n-2) = 8 + 5 = 13
还可以转换为递归写法
def climbStairs(n):if n <= 1:return 1return climbStairs(n-1) + climbStairs(n-2)至此,就是暴力算法的解题思路,所有可能的组合都做一遍。
(3)动态规划(DP):解题思路
依据上面算法特征分析的基础上,使用一个数组动态存储n的计算结果。
初始化数组,预先存入n-1和n-2的结果
def climbStairs(n):if n <= 1:return ndp = [i for i in range(n+1)]for i in range(3,n+1):dp[i] = dp[i-1] + dp[i-2]return dp[-1]上面代码中的dp就是我们提到的数组,其中
dp[i] = dp[i-1] + dp[i-2]。循环执行完成后,数组中最后一次计算的结果就是爬n阶楼梯的方法数。
- 时间复杂度:O(n)
- 空间复杂度:O(n)
对于空间复杂度,还可以进一步优化。由于我们只考虑n以及n-1、n-2的值。所以,中间的过程值可以丢弃。定义一个固定长度的数组,每次计算结果动态覆盖,如下:
def climbStairs(n):if n <= 1:return ndp = [0,1,2]for i in range(3,n+1):sum = dp[1] + dp[2]dp[1] = dp[2]dp[2] = sumreturn dp[2]- 时间复杂度:O(n)
- 空间复杂度:O(1)
(4)动态规划理论
学习动态规划算法,是从多种题解的思路中学习和发现。众多技术高手都给出了思路和技巧,但从实际出发,建议还是先埋头做题,积累了练习和分析思考后,再进行看高手的总结和归纳才会有“英雄所见略同”的共识。
在这之前,针对每道题目的分析,希望能思考如下的几个问题:
-
题目计算的目标是什么
走台阶问题的目标是求走法组合总数。
-
计算分解的子问题是什么
(n-1)阶走法 、(n-2)阶走法就是n阶走法的子问题 ****
-
转移方程是否是子问题的组合
转移方程上面已经写出来了 f(n) = f(n-1)+f(n-2) 。
-
能否优化
使用动态数组或字典来存储中间结果,可以有效的减少重复计算的复杂度。
当然,涉及到使用数组等容器来实现计算和优化时,还会接触到背包问题。
2.2 力扣题之海盗船长
问题:海盗船长:. - 力扣(LeetCode)
海盗船长:船长从坐标为(0,0)的位置出发,每次只能向x轴,y轴正方向走一步,求走到x,y点有几种走法?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:n = 3, n = 2
输出:3
解释:从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 10^9
(1)解题思路1:
从[0,0]到[x,y],是一个从矩阵左上角向右、向下探索的过程。
想要到达[x,y]位置,必然经过[x-1,y]或者[x,y-1]

所以,路径问题的分解就是求[x , y] = [x-1,y] + [x,y-1]
设 m,n = 3,7 暴力解法
results = {}def path_count(x, y):# results = {}if x == 1 or y == 1:results[(x,y)] = 1return 1results[(x,y)] = path_count(x-1,y) + path_count(x,y-1)return results[(x,y)]print(path_count(3,7))
时间复杂度:O(mn)
空间复杂度:O(n)
(2)解题思路2:
观察上面的方案,可以发现分解的路径实际上存在着大量重复的计算
print(results)

我们可以思考:走到results中(m,n)位置的上一步,一定是(m-1,n),(m,n-1),(m-1,n-1)的位置。

这其中(m-1,n-1)走过的路径中,就包含了(m-1,n)和(m,n-1)走过的路径。
以此类推,所有(m-2,n-2)的路径中,也就包含了(m-1,n-1), (m-1,n), (m,n-1) …… 如此嵌套。我们把计算结果存储在results里面,再次遇到相同的计算时,就直接把结果提取出来。
def path_count(x, y):if x == 1 or y == 1:results[(x,y)] = 1return 1# 查找重复节点,直接返回计算后结果if (x,y) in results:return results[(x,y)]results[(x,y)] = path_count(x-1,y) + path_count(x,y-1)return results[(x,y)]
(3)动态规划:解题思路3:
动态规划方式实现:
转移方程:f(x,y) = f(x-1,y) + f(x, y-1)
分两步实现:
-
计算“到达”每个位置所需要的步数(初始为1)
m,n = 3,7 path_counts = [[1] * n for j in range(m)] for i in range(m):for j in range(n):print(path_counts[i][j], end=' ')print() -
计算从起始位置,到达当前位置,步数的累加和
for x in range(1,m):for y in range(1,n):path_counts[x][y] = path_counts[x-1][y] + path_counts[x][y-1]print(path_counts[m-1][n-1])
完整代码:
def path_count(x, y):path_counts = [[1] * y for j in range(x)]for i in range(1,x):for j in range(1,y):path_counts[i][j] = path_counts[i-1][j] + path_counts[i][j-1]return path_counts[x-1][y-1]
相关文章:

【数据结构和算法】三、动态规划原理讲解与实战演练
目录 1、什么是动态规划? 2、动态规划实战演练 2.1 力扣题之爬楼梯问题 (1)解题思路1: (2)解题思路2: (3)动态规划(DP):解题思路 (4&#x…...
)
交叉编译 perl-5.40.0(riscv64)
交叉编译 perl-5.40.0(riscv64) https://arsv.github.io/perl-cross/usage.html https://github.com/arsv/perl-cross 借助 perl-cross 进行交叉编译 https://www.perl.org/get.html#unix_like 这里获取 perl-5.40.0 的源码 https://github.com/arsv/pe…...

Leetcode 搜索旋转排序数组
这段代码是用于解决LeetCode第33题“搜索旋转排序数组”的Java解法。以下是对该算法思想的中文解释: 算法思想 二分查找的基本思路: 由于数组是部分有序的(被旋转过),我们可以利用二分查找的思想,逐步缩小…...

Spring Task—定时任务
Spring Task 是 Spring 提供的一种轻量级定时任务调度功能,内置在 Spring 框架中。与 Quartz 等重量级调度框架相比,Spring Task 使用简便,无需额外依赖,适合在简单的调度任务场景中使用。通过注解配置方式,开发者可以…...

Spring Boot 应用开发概述
目录 Spring Boot 应用开发概述 Spring Boot 的核心特性 Spring Boot 的开发模式 Spring Boot 在企业应用开发中的优势 结论 Spring Boot 应用开发概述 Spring Boot 是由 Pivotal 团队开发的一个框架,基于 Spring 框架,旨在简化和加速基于 Spring …...

Chrome谷歌浏览器加载ActiveX控件之allWebDesktop控件介绍
背景 allWebDesktop控件是一款方便用户在线打开各类文档的OA办公控件。它设计比较轻巧,充分利用计算机程序资源打开文档,并将程序窗口嵌入到allWebDesktop控件区域内,从而实现浏览器内打开各类文档效果。 allWebPlugin中间件是一款为用户提供…...
GitHub Star 数量前 5 的开源应用程序生成器
欢迎来的 GitHub Star 数量排名系列文章的第 7 篇——最受欢迎的应用程序生成器。 之前我们已经详细探讨过:在 GitHub 上最受欢迎的——无代码工具、低代码项目、内部工具、CRUD项目、自部署项目和 Airtable 开源替代品。累计超过 50 个优质项目!&#…...

DBC文件当中新建CANFD等类型的报文
同学最近有添加CANFD报文的需求,需要用到CANFD类型报文的DBC文件,这下就难住我了,我之前用的DBC文件只有“CAN Standard”“CAN Extended”两种类型,压根没见过FD的。 后来他找到了项目之前的DBC,打开来看,…...
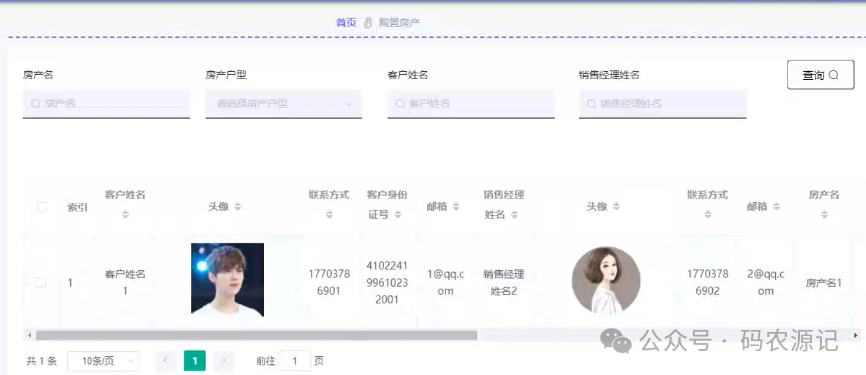
基于SpringBoot的房地产销售管理系统【附源码】
基于SpringBoot的房地产销售管理系统(源码L文说明文档) 目录 4 系统设计 4.1用户登录功能的详细实现 4.2管理员权限的功能实现 4.2.1客户信息管理功能的详细实现 4.2.2房产管理功能的详细实现 4.2.3预约看房功能的详细实现 4.2.4论…...

圆点虚线 Android
参考 https://blog.csdn.net/l_o_s/article/details/73550876 <com.xxx.wwww.weight.PointDividerViewandroid:layout_width"match_parent"android:layout_height"wrap_content"app:PDbackgroundColor"color/white"app:dotColor"color/…...

贵州鑫宏远农业-始终致力于推动现代农业的科技创新与发展
贵州鑫宏远农业科技有限公司,是一家在高科技农业领域深耕细作、锐意进取的企业。自成立以来,我们始终致力于推动现代农业的科技创新与发展,业务全面覆盖农业科学研发、组织培养生产、专业育苗培植、半成品及成品精细化养护、市场销售以及全方…...

程序员做销售,从代码到客户的逆袭之路
大家好,我是小悟。 在这个互联网风起云涌、技术迭代日新月异的时代,“跨界”已然成为一种新潮流。就好似那从天而降的大侠,一不小心就可能横跨了数个充满奇遇与挑战的领域。 想象一下,一个平日里只跟代码打交道的程序员…...

Flink CDC系列之:理解学习Kubernetes模式
Flink CDC系列之:理解学习Kubernetes模式 准备会话模式启动会话集群设置 Flink CDC提交 Flink CDC Job Kubernetes 是一种流行的容器编排系统,用于自动化计算机应用程序的部署、扩展和管理。Flink 的原生 Kubernetes 集成允许您直接在正在运行的 Kuberne…...

git合并相关操作详解
在使用Git进行分支管理时,合并(merge)操作是非常常见的。下面是Git合并相关的详细步骤和一些常见的场景及注意事项。 一、 基本合并操作 假设我们有两个分支:main 和 feature,希望将 feature 合并到 main 上。 切换到目标分支 首先需要切换到你想合并到的分支。例如,切…...

前端经典【面试题】持续更新HTML、CSS、JS、VUE、FLUTTER、性能优化等
HTML/CSS 面试题 什么是语义化 HTML? 说明:语义化 HTML 使用 HTML 标签来描述内容的含义,而不仅仅是其外观。使用语义化标签可以提高可读性和可访问性,并对 SEO 友好。示例: <header><h1>网站标题</h1&…...

【Linux知识】linux磁盘管理深入了解
文章目录 常见磁盘管理命令行磁盘分区NASNAS 磁盘挂载🔐 如何设置NAS设备的访问权限? Mkfs🧐 mkfs 命令支持哪些文件系统类型? Mount🔑 在Linux中,如何安全地卸载挂载的文件系统? 常见磁盘管理命…...

Qt Essential Classes
目录 QVariant QFlags QRandomGenerator 经典的Qt容器 QVector QList QMap QMultiMap QSet QHash QVariant 同std::variant是一样的,他是一个更加高级的union。在一个时间下,它虽然实际上只能是一种类型,但是一个variant可以hold住…...

小小猫棒onu替换家用光猫,薅运营商带宽羊毛,突破1000M
小小猫棒onu 一、总体步骤 1 记录原来光猫信息 主要包括SN,ploam密码,loid、loid密码、 mac、上网的vlan id等 一般gpon采用SN、ploam密码、SNploam密码三种中的一种认证方式 一般Epon采用loid(逻辑id)、mac、loid mac三种中…...

软件测试学习笔记丨Selenium学习笔记:css定位
本文转自测试人社区,原文链接:https://ceshiren.com/t/topic/22511 本文为霍格沃兹测试开发学社的学习经历分享,写出来分享给大家,希望有志同道合的小伙伴可以一起交流技术,一起进步~ 说明:本篇博客基于sel…...

python数据处理常用操作
数据处理是机器学习中非常重要的一步,以下是一些常用的操作和示例代码: 1. 数据清洗 处理缺失值: import pandas as pd# 读取数据 df pd.read_csv(data.csv)# 删除缺失值 df.dropna(inplaceTrue)# 用均值填充缺失值 df.fillna(df.mean(), i…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
