【去哪里找开源商城项目】
有很多途径可以找到开源项目,以下是一些常用的方法:
-
开源代码托管平台:许多开源项目都托管在平台上,例如GitHub、GitLab和Bitbucket。你可以在这些平台上浏览项目,搜索关键词,查看项目的星级和贡献者数量等。
-
社区论坛和邮件列表:许多开源项目有官方的社区论坛或邮件列表,你可以在这些地方找到项目的最新消息、讨论和寻找志同道合的开发者。
-
搜索引擎:使用搜索引擎如Google、Bing或DuckDuckGo,搜索关键词加上"开源项目",可以找到一些相关的项目列表或资源。
-
开源软件推荐网站:有一些网站专门收集和推荐开源软件,例如opensource.com、AlternativeTo和LibreProjects等。
-
社交媒体和技术博客:关注一些知名的开发者或技术博客,他们通常会分享一些值得关注的开源项目。
在寻找开源项目时,建议先确定自己的兴趣和技能,然后选择合适的项目进行贡献。同时,阅读项目的文档和社区规范,了解项目的愿景、目标和贡献方式,这有助于你更好地融入项目并与其他贡献者协作。
相关文章:

【去哪里找开源商城项目】
有很多途径可以找到开源项目,以下是一些常用的方法: 开源代码托管平台:许多开源项目都托管在平台上,例如GitHub、GitLab和Bitbucket。你可以在这些平台上浏览项目,搜索关键词,查看项目的星级和贡献者数量等…...
ei会议检索:第二届网络、通信与智能计算国际会议(NCIC 2024)
第二届网络、通信与智能计算国际会议(NCIC 2024)将于2024年11月22-25日在北京信息科技大学召开,聚焦网络、通信与智能计算,欢迎国内外学者投稿交流,录用文章将在Springer出版,并提交EI等检索。 NCIC 2024&a…...

vue添加省市区
主要参考“element”框架:Element - The worlds most popular Vue UI framework <div class"block"><span class"demonstration">默认 click 触发子菜单</span><el-cascaderv-model"value":options"optio…...

运维监控丨16条常用的Kafka看板监控配置与告警规则
本期我们针对企业运维监控的场景,介绍一些监控配置和告警规则。可以根据Kafka集群和业务的具体要求,灵活调整和扩展这些监控配置及告警规则。在实际应用场景中,需要综合运用多种监控工具(例如Prometheus、Grafana、Zabbix等&#…...

ECharts饼图,配置标注示例
const color ["#00FFB4", "#5498FD", "#6F54FD", "#FD5454", "#FDA354",]const datas [{ value: 100, name: "一年级" },{ value: 70, name: "二年级" },{ value: 184, name: "三年级" },{…...

【大象数据集】大象图像识别 目标检测 机器视觉(含数据集)
一、背景意义 在信息时代,数据的收集和分析技术得到了飞速发展。深度学习算法的出现,为处理和分析这些复杂的鱼类数据集提供了强大的工具。深度学习具有强大的模式识别和特征提取能力,能够从海量的数据中自动学习和发现规律,为鱼…...

LN 在 LLMs 中的不同位置 有什么区别么
Layer Normalization(LN)是一种在深度学习中用于稳定和加速神经网络训练的归一化技术。它通过对单个样本的所有激活进行归一化来工作,与Batch Normalization(BN)不同,BN是对一个mini-batch中的所有样本的激…...

【代码随想录Day57】图论Part08
拓扑排序精讲 题目链接/文章讲解:代码随想录 import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner new Scanner(System.in);// 读取文件数量 n 和依赖关系数量 mint n scanner.nextInt();int m scanner.nextInt()…...

记录一次mmpretrain训练数据并转onnx推理
目录 1.前言 2.代码 3.数据形态【分类用】 4.配置文件 5.训练 6.测试-分析-混淆矩阵等等,测试图片效果等 7.导出onnx 8.onnx推理 9.docker环境简单补充 1.前言 好久没有做图像分类了,于是想用商汤的mmclassification快速搞一波,发现已…...

shodan5,参数使用,批量查找Mongodb未授权登录,jenkins批量挖掘
查找美国安全局漏洞 nww.nsa.gov(美国安全局官方网站) net参数使用 搜索指定的ip网段 shodan search --limit 10 --fields ip_str,port net:208.88.84.0/24 (老美国家安全局的一个网段)可能直接访问不太行,可以使用host参数,得到域名再去…...

telnet 密码模式 访问路由器
telnet 密码访问华为路由器 模拟被访问路由 sy [Huawei]int g0/0/0 //选中 g0/0/0端口 [Huawei-GigabitEthernet0/0/0]ip add 192.168.1.1 24 //设置端口ip [Huawei]user-interface vty 0 4 //配置vty [Huawei-ui-vty0-4]set authentication password cipher huawei123 //设置…...

文心一言 VS 讯飞星火 VS chatgpt (380)-- 算法导论24.4 12题
十二、给出一个有效算法来解决 A x ⩽ b Ax⩽b Ax⩽b 的差分约束系统,这里 b b b 的所有元素为实数,而变量 x i x_i xi 中某个给定的子集是整数。如果要写代码,请用go语言。 文心一言: 差分约束系统问题通常用于解决带有约…...
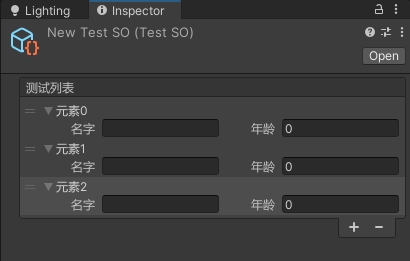
Unity自定义数组在Inspector窗口的显示方式
了解 单行高度:EditorGUIUtility.singleLineHeight获取 PropertyField 控件所需的高度:EditorGUI.GetPropertyHeight属性是否在Inspector窗口展开:SerializedProperty.isExpanded可重新排序列表类:ReorderableList绘制纯色矩形:EditorGUI.Dr…...
--SPCL论文阅读笔记(2024-10-29))
ERC论文阅读(03)--SPCL论文阅读笔记(2024-10-29)
SPCL论文阅读笔记 论文中心思想 这篇论文是研究ERC任务的论文,作者提出了监督原型对比学习的方法用于ERC任务。 论文 EMNLP2022 paper “Supervised Prototypical Contrastive Learning for Emotion Recognition in Conversation” 现存问题 现存的使用监督对…...

Straightforward Layer-wise Pruning for More Efficient Visual Adaptation
对于模型中冗余的参数,一个常见的方法是通过结构化剪枝方法减少参数容量。例如,基于幅度值和基于梯度的剪枝方法。尽管这些方法在传统训练上通用性,本文关注的PETL迁移有两个不可避免的问题: 显著增加了模型存储负担。由于不同的…...

喜讯 | 创邻科技杭州电子科技大学联合实验室揭牌成立!
近日,杭州电子科技大学图书情报专业硕士行业导师聘任仪式暨杭电-创邻图技术与数字化联合实验室(图书档案文物数字云联合研发中心)揭牌仪式在杭州电子科技大学隆重举行。杭州电子科技大学原副校长吕金海、研究生院副院长潘建江,科研…...

海外媒体发稿:如何打造媒体发稿策略
新闻媒体的发稿推广策略对于提升品牌知名度、吸引流量以及增加收入非常重要。本文将介绍一套在21天内打造爆款新闻媒体发稿推广策略的方法。 第一天至第七天:明确目标和定位 在这个阶段,你需要明确你的目标和定位,以便为你的新闻媒体建立一个…...

PyTorch模型保存与加载
1.保存与加载的概念(序列化与反序列化) 模型训练完毕之后,肯定想要把它保存下来,供以后使用,不需要再次去训练。 那么在pytorch中如何把训练好的模型,保存,保存之后又如何加载呢? 这就用需要序列化与反序列化,序列化与反序列化的概念如下图所示: 因为在内…...
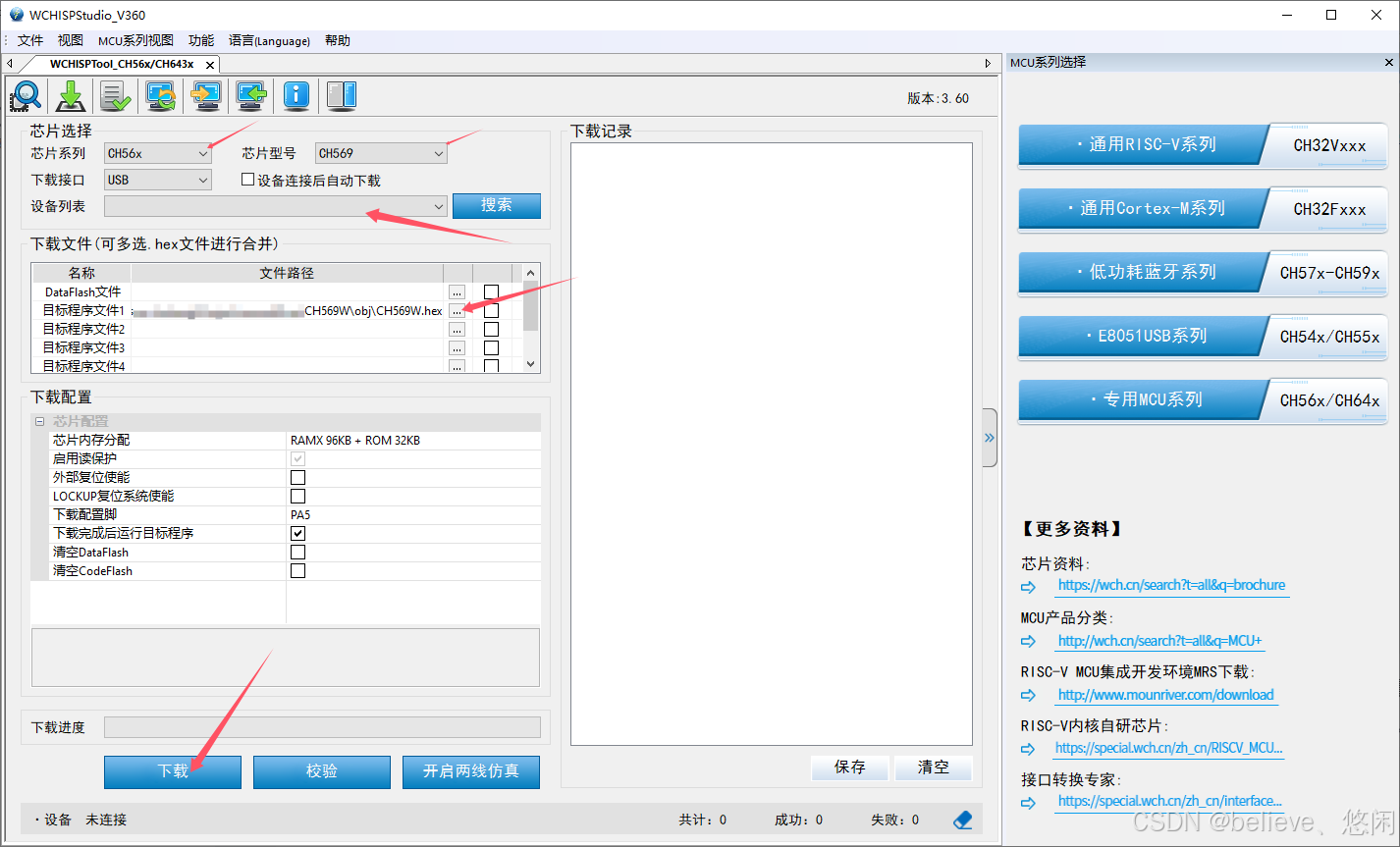
CH569开发前的测试
为了玩转准备Ch569的开发工作 ,准备了如下硬件和软件: 硬件 1.官方的 Ch569 开发板,官方买到的是两块插接在一起的;除了HSPI接口那里的电阻,这两块可以说是一样的。也意味着两块板子的开发也需要烧录两次;…...
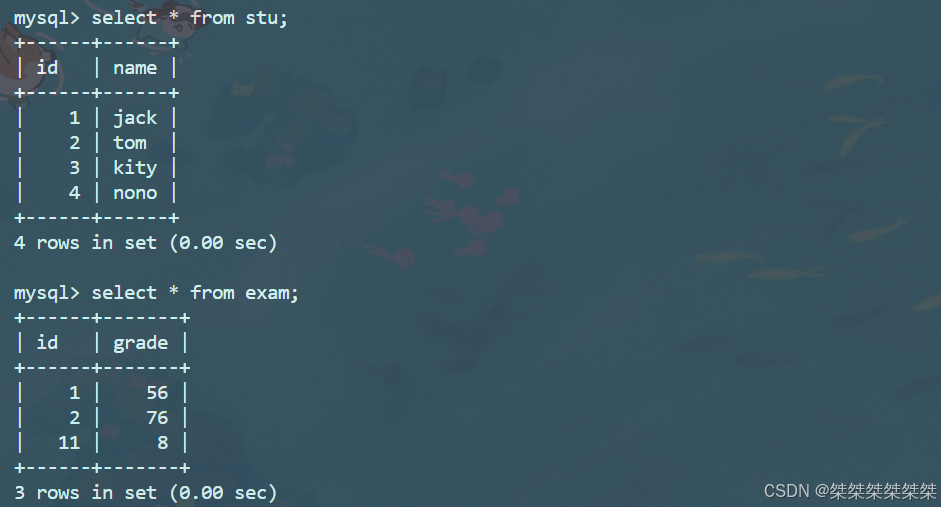
MySQL中表的外连接和内连接
内连接和外连接 表的连接分为内连接和外连接,内连接就是将需要连接的表形成笛卡尔积筛选;外连接分为左外连接和右外连接,左外连接为左侧的表需要完全显示,右外连接为右侧的表现需要完全显示。 文章目录 内连接和外连接内连接外…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
